双边定数截尾下Weibull分布参数的Bayes估计

程 静,周菊玲

(新疆师范大学 数学科学学院,新疆 乌鲁木齐 830017)

0 引言

Weibull分布是一种常见的寿命分布,经常用于可靠性工程、生存分析、电力工程、管理科学等众多领域许多学者[1-5]在双边定数截尾下,基于不同损失函数分别研究了广义指数分布、Pareto分布、Burr Ⅻ分布、指数-威布尔分布和Topp-Leone分布参数的Bayes估计,且都利用随机模拟对所得的估计结果进行了进一步的分析;其中邓严林[5]还算出了未知参数的估计及预测值和预测区间;魏艳华[6]等在定数截尾样本下利用混合Gibbs算法研究了逆威布尔分布参数的Bayes估计并进行了数值模拟,最终结果表明该算法是可行的;龙兵[7]在定数截尾样本下研究了艾拉姆咖分布参数在不同损失函数下的Bayes估计,并利用数值模拟对各个估计结果优良性进行了分析;成军祥[8]在不同的截尾数据下,研究了Weibull分布参数的极大似然估计.

假设X是服从两参数Weibull分布的随机变量,其分布函数为

密度函数为

故可靠度以及失效率分别为

其中η为尺度参数,β为形状参数,且尺度参数η是未知的记为Weib(η,β).

在某些场合中,可以令α=η-β,则分布函数及密度函数如下

F(X)=1-e-αxβ,α>0,β>0

(1)

f(x)=βαxβ-1e-αxβ,α>0,β>0

(2)

可靠度为

R(X)=e-αxβ,α>0,β>0.

上述α为尺度参数,β为形状参数,记为Weib(α,β).

1 极大似然估计

在双边定数截尾样本下进行寿命试验,具体方案:假设有一批产品的寿命服从Weibull分布(1),从中随机抽取n个产品进行试验,规定到r个( 0 ≤r≤n) 产品失效时该试验终止,即定数截尾试验,把观察到的次序失效数据设为x1≤x2≤ … ≤xr.但因为一些外部及实验手段等原因,导致现实操作过程中会有部分数据未被观察到,假设前s-1个数据丢失,此时把观测到的次序统计量为:xs≤x(s+1)≤…≤xr,1≤s≤r≤n记为双边定数截尾样本在双边定数截尾样本下,当产品服从Weibull分布时,记x=(xs,xs+1,…,xr-1,xr),可得样本(xs,xs+1,…,xr-1,xr)的联合分布密度函数为

(3)

将式(1)和式(2)代入式(3),可得

(4)

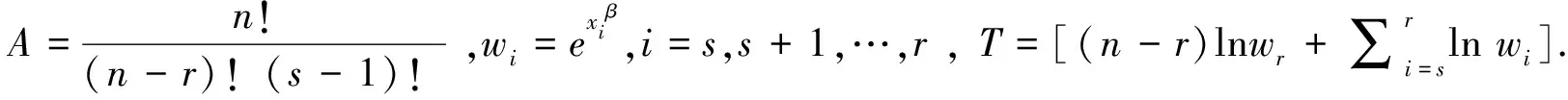
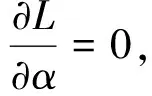
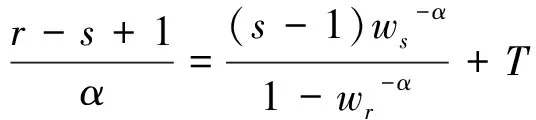
(5)

2 Bayes估计

2.1 无信息先验下参数α的Bayes估计

把参数α当作随机变量,当先验分布选为无信息先验分布时,分布密度为

(6)

由式(4)和式(6)得α的后验密度为

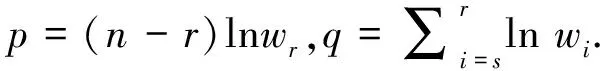
2.1.1 刻度平方误差损失函数下的Bayes估计

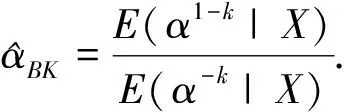
在刻度平方误差损失函数下,Weibull分布参数α的Bayes估计为

证明利用α的后验分布有

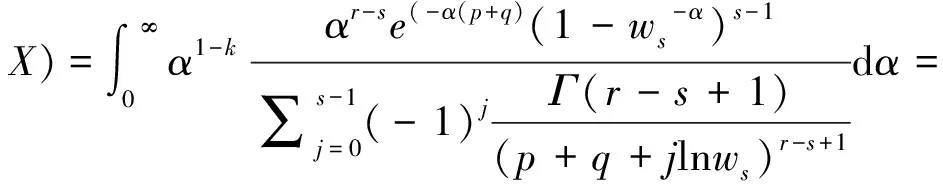
同理可得

从而得到

证毕.

2.1.2 Linex损失函数下的Bayes估计

Linex损失函数的表达式为

关于等式两边对参数α同时求后验期望得

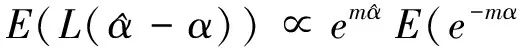
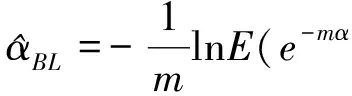
(7)

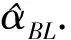
在Linex损失函数下Weibull分布尺度参数α的Bayes估计为

证明由式(7)可得

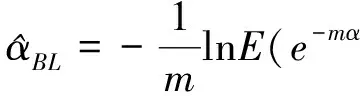
2.2 共轭先验下参数α的Bayes估计

把参数α当作随机变量,先验分布选为共轭先验Γ-分布族Γ(a,b),分布密度为

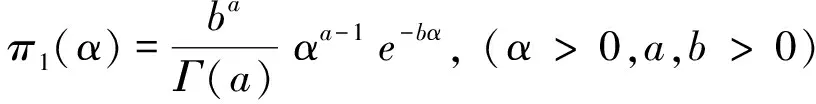
(8)

联合式(4)和式(8),α的后验密度为

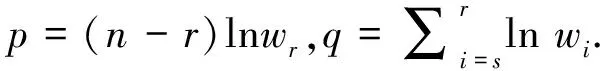
2.2.1 刻度平方误差损失函数下的Bayes估计

在刻度平方误差损失函数下,对于给定的先验分布式(8),Weibull分布参数α的Bayes估计为

证明利用α的后验分布(h1(α|x)有

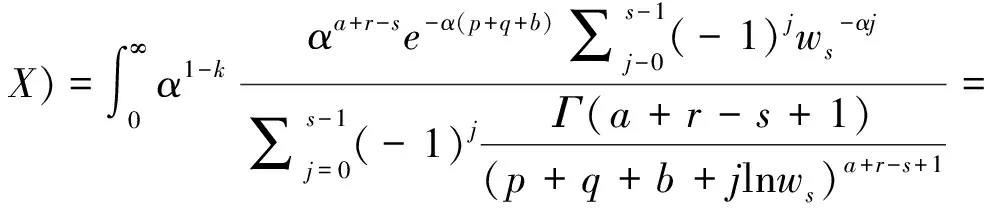
同理可得

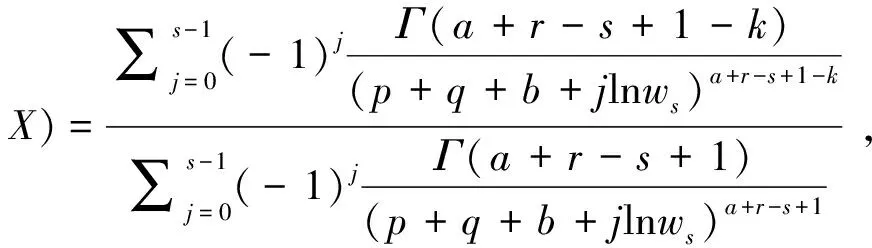
从而得到

证毕.

2.2.2 Linex损失函数下的Bayes估计

在Linex损失函数下Weibull分布尺度参数α的Bayes估计为

证明由式(7)可得

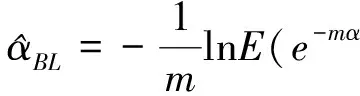
3 多层Bayes估计

从上述内容易知,α的Bayes估计仍有超参数a,b,因为需要进一步讨论θ的多层Bayes估计.所以此时把超参数看成相互独立的随机变量,再给出一个先验,称为超先验,进而求得α的多层Bayes估计.当Γ(a,b)分布的超参数00时,a,b先验分布分别为均匀分布,即

π2(a)=U(0,1),π2(b)=U(0,g).

上式的g是一个常数且不适合过大,因为当先验分布的尾部越窄,所对应的Bayes估计的稳健性越差.

α的多层先验密度函数为

(9)

定理1 基于Weibull分布,把式(9)作为α的先验分布,则在刻度平方误差损失、Linex损失函数下,α的多层Bayes估计分别为

证明先证刻度平方误差损失函数下α的多层Bayes估计为

首先α的后验密度是

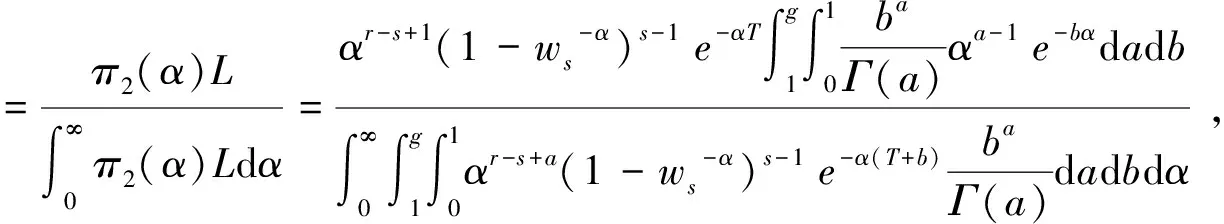
其次α的多层Bayes估计为

接着证明Linex损失函数下α的多层Bayes估计为

4 随机模拟

表1 不同损失函数下参数α的Bayes估计

由表1可见,无论在刻度平方误差损失下还是Linex损失下Γ先验分布都比无先验分布下的Bayes估计好.但是当在刻度平方误差损失下,选用Γ先验分布时,参数α的估计结果更接近真实值.

5 结论

基于双边定数截尾Weibull分布寿命试验数据,结果表明在刻度平方误差损失函数下得到的Bayes估计比Linex损失下更接近真值.