基于脉冲功率合成技术的宽微带分幅成像驱动技术研究
魏师铎,缑永胜,杨阳,冯鹏辉,刘百玉,田进寿,王旭,刘恒博,徐晗滔,杨懿豪
(1 中国科学院西安光学精密机械研究所 超快诊断技术重点实验室,西安 710119)
(2 中国科学院大学,北京 100049)
(3 中国科学院大学 材料与光电研究中心,北京 100049)
0 引言
当上升时间约100 ns、幅值数10 MA 的脉冲电流作用于金属丝阵或喷气负载时,负载会迅速电离并形成等离子体。由于洛伦兹力的作用这些等离子体将快速向轴线聚爆并最终在中心滞止,形成高温高密度等离子体并进一步辐射出强X 射线,这一过程被称为Z 箍缩[1]。几十年以来,Z 箍缩被广泛应用于高能量密度物理研究,包括辐射源开发、辐射驱动科学、动态材料特性、磁惯性聚变和惯性约束聚变等[2-3]。为了探究在超小空间和超快时间尺度下物质的结构、性质与运动规律[4],以变像管分幅相机技术等为代表的超快现象的研究测量技术成为人们使用的主要工具。
X 射线分幅相机在Z 箍缩过程中被广泛应用于等离子体二维成像[5]。X 射线分幅成像系统主要由成像针孔阵列及其调节装置、X 射线像增强器、高压驱动电脉冲产生器、图像记录与处理系统以及程控系统组成。其中X 射线像增强器由微通道板和制作在光纤面板上的荧光屏组成。微通道板(Microchannel Plate,MCP)的输入面镀有X 射线光电阴极。实验靶产生的X 射线通过针孔板成像到相机的每条独立阴极微带线上。当选通脉冲没有作用在光阴极上时,MCP 会吸收X 射线图像,荧光屏就无法成像。只有当选通脉冲作用在微带光阴极上时,X 射线图像在MCP 上产生的光电子将获得增益并产生可见光图像输出在荧光屏上。所获得的图像再由相应的相机或者CCD 处理。
定义选通电脉冲通过相邻光阴极间微带线所用时间为画幅间隔时间,它是固定的。每一幅像的曝光时间由选通电脉冲的半高宽度(下称脉宽)和分幅管的特性共同决定,不同等效阻抗的MCP 会实现不同画幅的分幅相机成像。超宽画幅行波选通分幅相机的MCP 传输微带线的宽度达到20 mm、长度达95 mm、等效阻抗约6 Ω。想要驱动这种分幅管需要电场峰值超过3 kV、脉冲持续时间在纳秒或者百皮秒量级、频谱宽度为几十兆赫兹到几千兆赫兹的选通脉冲。为了获得这样的高压脉冲,比较成熟的技术是基于雪崩晶体管设计串并联相结合的Marx 脉冲产生电路,从而产生纳秒高压脉冲。但受制于晶体管器件自身的特性,产生幅度高于5 kV 前沿优于100 ps、抖动优于20 ps 的脉冲源已经接近电子学技术极限[6]。想要获得更高功率选通脉冲就需要采用多路脉冲功率合成技术。
脉冲的功率耦合是将多路脉冲在同一时刻完成能量上的叠加从而形成功率更高且脉宽与前沿都变化不大的脉冲。常见的功率耦合主要有芯片式功率合成、空间功率合成、电路式功率合成等几种合成方式。芯片式功率合成技术[7]有着不错的合成效率与稳定性,但是频带增大会使其电路匹配变得困难,造成损耗增加使合成效率降低,同时体积小带来的散热问题也是制约其发展的因素之一;空间功率合成[8-9]是主要针对毫米波领域提出的一种合成方式。与二者相比,以基于威尔金森功分器[10]和传输线变压器法[11]的电路式功率耦合的方法更适合高压脉冲的耦合。
回顾以往的相关探究,YAN K 等利用传输线变压器设计出一种10 kW 高压脉冲发生器,脉冲幅度为30~100 kV,上升时间约为20 ns,持续时间为50~250 ns,平均功率高达10 kW,总能量传输效率约为80%~90%[12]。KRISHNASWAMY P 等利用特殊的传输线的结构成功阻抗匹配了8 级Marx 电路,随后获得峰值幅度1.1 kV、上升时间为800 ps 及重频200 kHz 的脉冲信号[13]。梁勤金将36 路2 MW 的高压脉冲通过传输线变压器的方法合成功率可达57.6 MW/50 Ω 的高压纳秒脉冲,重频在1 kHz,合成效率在80%以上[14]。李江涛等通过改进Marx 电路PCB 排布形式设计一种新型的立体结构,它将四路模块控制延迟以完成同步叠加,最终产生幅值-5.0 kV、半高脉宽5.3 ns、重频达10 kHz 的脉冲信号,计算得到四路脉冲叠加效率达到了96.2%[15]。2010 年石小燕等利用传输线变压器在50 Ω 的负载上完成4.5 kV 的4 路脉冲的功率合成,合成之后的脉冲峰值达到8.8 kV,脉宽约6.5 ns,脉冲上升时间约2.1 ns[16]。张峰平等基于传输线变压器设计出2~30 MHz 的5 kW/50 Ω 四路功率合成器,性能良好[11]。孙正淳等在500 MHz~2.5 GHz 频带内将上升沿162 ps、半峰脉宽537 ps、峰值幅度3.8 kV 的4 路脉冲合成为前沿为200 ps、半峰脉宽557 ps、峰值幅度6.8 kV 的高压脉冲,合成效率为89%[17]。朱磊等利用Y 型节级联的方式实现四合一功率合成,实现在80 MHz~1 GHz 范围内合成效率在90%以上[18]。
分析相关研究可以看出,文献[12]、[14]的耦合效率不足,文献[13]耦合后的脉冲幅值仍有提高的空间,文献[11]、[15]~[18]虽然得到了较高的耦合效率,但其工作带宽有限。由此可见在宽频带内实现高效率的高压选通脉冲功率合成是研究的难点。考虑到基于传输线变压器的功率耦合工作带宽较窄,选择基于威尔金森结构的功分器的功率耦合的方法,将幅度较低的窄带脉冲通过功率耦合的方式合成为幅度满足要求的高压脉冲。利用多节阻抗变换器带宽的较宽的特点提高功率耦合的工作带宽,从而满足不同频谱的脉冲耦合。利用仿真软件设计工作频带在300 MHz~3 GHz 的功率耦合电路,使用gradient、hybrid 以及genetic等多种算法优化传输线等效阻抗和隔离电阻的取值使其实现高效率的耦合。结合前级的高压窄脉冲输出和同步控制电路,可以实现8 路高压脉冲的功率耦合,从而获得可用于驱动宽20 mm、长95 mm、等效阻抗6 Ω 左右的MCP,实现分幅相机成像的超宽带高压脉冲。目前基于本技术的高压驱动脉冲源已应用于Ⅰ-MCP1.0型分幅相机。
1 基本原理
威尔金森功分器常用于微波电路中[19],它由威尔金森于1960 年提出[20],最早是一端输入八端输出的同轴结构,输出端口之间利用辐射状的隔离电阻进行阻隔。后因该结构容易发生谐振,高频特性差并且制作困难,很快就被平面式的功分网络替代[21],即现在常见的形式。威尔金森功率分配器的特点是结构简单、隔离度高、损耗小、各个端口同时匹配[22]。它通过引入隔离电阻使普通功分器变为有耗三端口网络,使得各个端口有了很好的隔离特性。
图1 为单节一分二等功分威尔金森功分器,设定其输入与输出微带线特征阻抗为Z0。为了满足需求,信号从端口2 和3 输入时,输出端口1 没有反射。因此经λ/4 传输线到端口1 的并联电导应满足,所以根据阻抗匹配原理,λ/4 传输线的特征阻抗。为了使R起到隔离电阻的作用,需要当信号从1 端口输入时,在2、3 端口得到幅相一致的输出信号,而当2 端口有信号输入时,电阻R可使分别到达3 端口的两路信号相互抵消[23]。同样根据阻抗匹配的原则可以推出
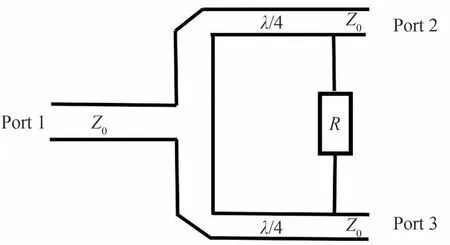
图1 单节一分二等功分威尔金森功分器Fig.1 Single section one-divided-two Wilkinson power divider
根据互易定理,将威尔金森功分器的输入输出反相即可实现多路信号或者脉冲的耦合,以下用功分器来替代耦合器的说法。研究表明,单节的威尔金森功分器工作带宽很窄,往往只有理论计算的20%,所以采用多节λ/4 传输线阻抗匹配的方式扩展系统的工作带宽。图2 为多节功分器的结构示意,其中Z1、Z2、…、Zn分别是各节λ/4 传输线的特征阻抗,R1、R2、…、Rn分别为各节传输线之间的隔离电阻。在多节阶梯式阻抗变换器中,不同传输线连接处会对输入信号产生反射,如果利用传输线相移将这些反射中和掉一部分,则电路可以在更多的频点实现阻抗匹配,理论上功分器的工作带宽是没有限制的。然而实际设计时要考虑多节阻抗变换带来的插入损耗与电路尺寸的增大。所以在设计时应根据指标与实际需求选择合适的参数。
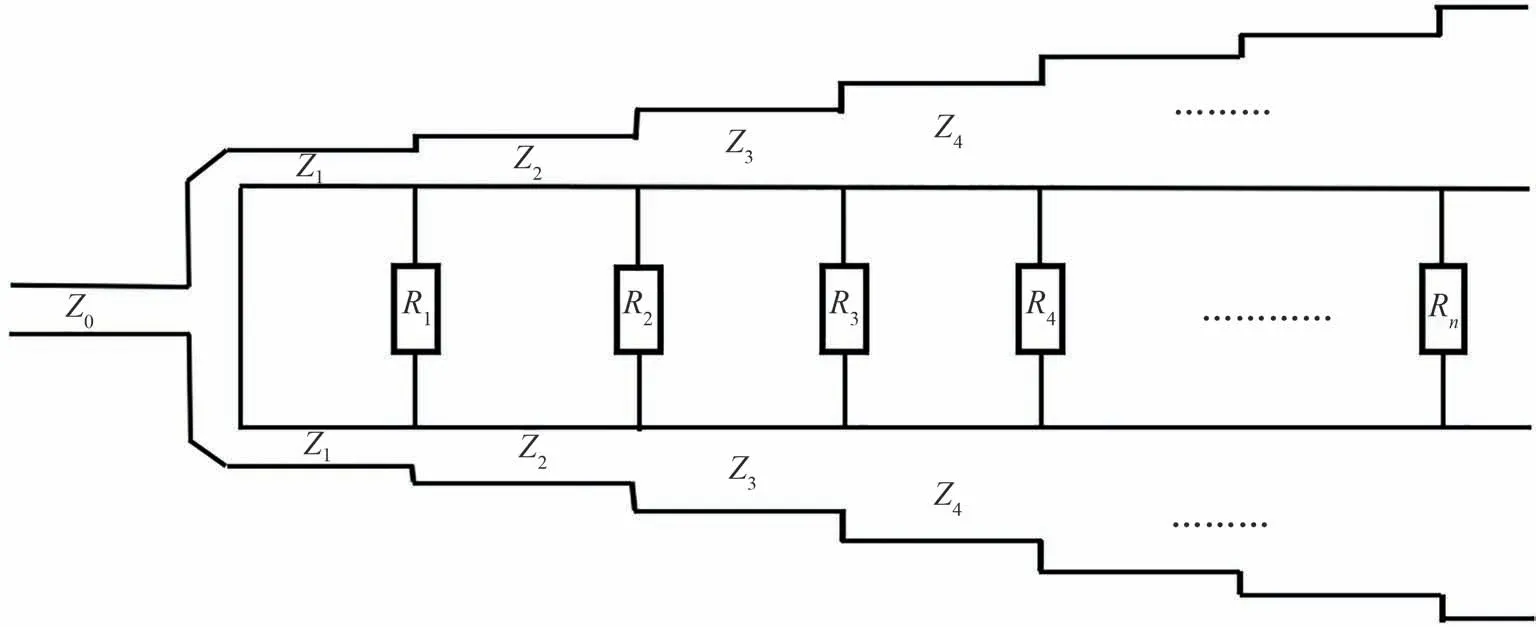
图2 多节一分二等功分威尔金森功分器Fig.2 Multi-section one-divided-two Wilkinson power divider
多节二等分威尔金森功分器一般利用奇偶模分析法可简化结构[24-25]。奇、偶模激励分别代表任意的两个相反和同相信号的叠加,再将二者得到的结果叠加起来就可代表网络任意激励下的结果。图3 是该模型下的信号反射情况。
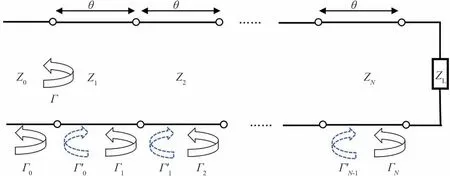
图3 奇偶模分析法下的信号反射情况Fig.3 Signal reflections under the parity mode analysis method
定义电磁波从第n节传输线到第n+1 节传输线的边界对应的反射系数为Γn,则有
假定每节传输线的特征阻抗从左到右依次增大,则总的反射系数响应可表示为
当N为偶数时,可表示为
当N为奇数时,可表示为
因为傅里叶级数可以在项数足够多时近似表示任意平滑的函数,设计时通过上述级数合理选择Γn以及节数就能得到想要的反射系数响应,之后再通过对比系数法就能得到传输线的特征阻抗。
奇模分析法用于分析各节传输线对应的隔离电阻。定义端口2、3 输入的反相激励电压为U0、-U0,则隔离电阻两端电压为2U0,中心线上电位为0,所以功分器连接点与输入端口1 的电位都是0。将之前求得的传输线等效阻抗以导纳的形式表达出来,再结合设定的指标,便可求得对应的隔离电阻。文献[26]给出了具体的推导公式,即
式中,yk为第k节传输线的导纳,gk为第k个隔离电阻阻值,ρℓ90°为阻抗变换器在90°时的端口驻波比,奇数阶取1,偶数阶取最大值。
通过以上分析,结合Cohn 提出通过增加级数来拓宽功分器的带宽的经验设计公式[27]及后续的改进设计公式[28],便可得到满足目标带宽功率合成与分配的模型初值,再结合软件的优化就可以得到实际电路会用到的传输线与隔离电阻的实际值。
除了宽频带特性,合成效率也是评判功率合成系统优劣的重要指标。最终的合成效率取决于输入到耦合系统的各路信号相位和幅度的一致性以及输入信号在耦合系统中的损耗。以N路功率合成网络为例,假设脉冲源1 输出的信号为a1=A1exp(jθ)=Aexp(jθ),设第i路信号与第1 路信号的幅度差为ΔAi,相位差为Δθi,则第i路信号为ai=Aiexp(jθi)=(A+ΔAi)exp(j(θ+Δθi))。仅考虑幅相不一致带来的损耗的前提下,如果负载等效阻抗为R,则系统的合成效率为
计算表明,幅度差在1 dB 以内、相位差在5°以内时,合成效率在99.6 以上,可以暂时忽略其影响,此时合成效率主要由电路损耗影响。
电路损耗主要由系统的介质损耗及反射损耗组成,研究表明当单路损耗为LdB 时,二进制N路合成效率与电路损耗的关系可表示为
所以设计的功率耦合系统在保证每路输入幅相一致性的前提下,要使单路插入损耗尽可能低。
2 设计与仿真
2.1 设计指标
工作频带:0.3~3 GHz。两路耦合时各端口驻波比(Voltage Standing Wave Ratio,VSWR)≤1.6。端口隔离度(S23)≤-15 dB。插入损耗(S21、S31 等)≥-3.5 dB。幅度一致性(Amplitude Consistency,AC)≤1 dB。相位一致性(Phase Consistency, PC)≤5°。
2.2 参数计算
为了满足电路的应用带宽及各方面的指标需求,确定工作频带为300 MHz~3 GHz,得到上限频率f2=3 GHz,下限频率f1=300 MHz,从而得到中心频率f0=1.65 GHz 及f2、f1对应的相角θ1=Π/11、θ2=10Π/11。相对带宽Wq=(3-0.3)/1.65≈1.64。利用第1 节的相关原理计算在工作频带内满足各指标要求时对应的功分器最小节数以及每节传输线对应的特征阻抗。其中最小节数N=7,功分器先采用7 节设计。根据理论分析可以计算出每节传输线归一化后的特征阻抗,即Z1=1.77 Ω、Z2=1.66 Ω、Z3=1.54 Ω、Z4=1.41 Ω、Z5=1.30 Ω、Z6=1.20 Ω 和Z7=1.13 Ω。取Z0=50 Ω,则Z1=88.7 Ω、Z2=82.985 Ω、Z3=76.82 Ω、Z4=70.71 Ω、Z5=65.085 Ω、Z6=60.255 Ω 和Z7=56.37 Ω;同理可确定每节传输线之间归一化的隔离电阻值,分别为R1=4.97 Ω、R2=2.59 Ω、R3=4.35 Ω、R4=6.40 Ω、R5=8.92 Ω、R6=13.32 Ω 和R7=8.85 Ω。取Z0=50 Ω,则R1=248.26 Ω、R2=129.62 Ω、R3=217.58 Ω、R4=319.9 Ω、R5=446.23 Ω、R6=666.145 Ω 和R7=442.48 Ω。
2.3 仿真与优化
首先将以上数据作为初值在仿真软件中搭建理想的一分二威尔金森功分器电路模型,其中元器件均为理想传输线与理想电阻,仿真结果如图4,可以看出隔离度不满足宽频带需求。

图4 初始参数仿真Fig.4 Initial parameter simulation
考虑到理想状态下的电路仿真需要保留较大的设计裕量,所以尝试增加传输线的节数,并使用gradient、hybrid以及genetic等多种算法优化传输线等效阻抗和隔离电阻的取值。最终选取具有12节微带线的二合一功率耦合电路模型。分别使用电路仿真软件和电磁模型软件对其进行电路仿真与电磁模型仿真。图5 为电路仿真结果,可以看出输入输出驻波比均小于1.4,隔离度仿真结果小于-15 dB,损耗小于0.5 dB。
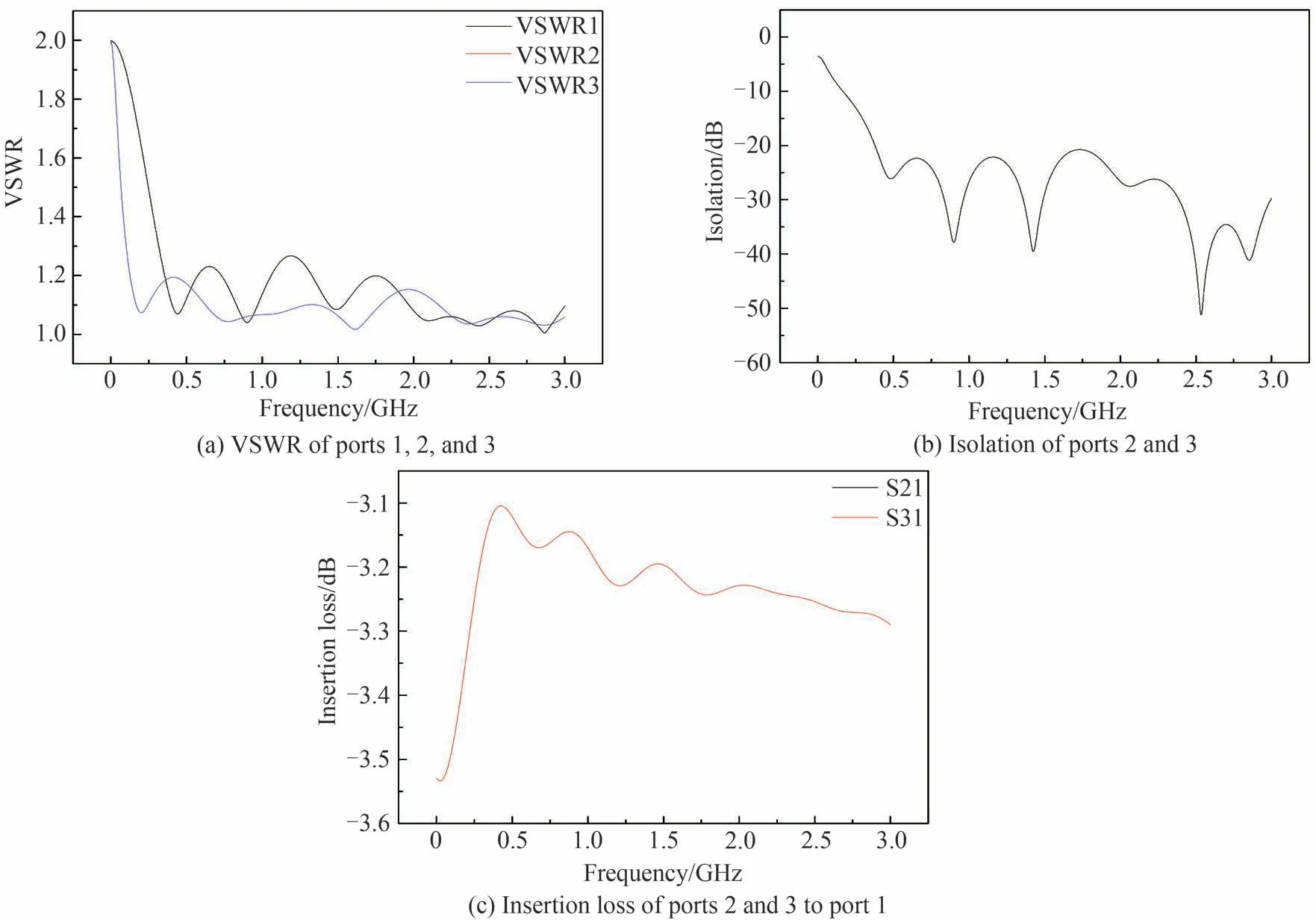
图5 优化仿真结果Fig.5 Simulation results of optimization
图6分别为电磁仿真软件对该器件的驻波比、插入损耗、端口隔离度和幅相一致性的仿真结果。由仿真结果可知,设计的单级功率耦合电路在工作频带内基本满足插入损耗小于0.5 dB,隔离度在13.8 dB 以上,输入端口驻波比小于1.6,输出端口驻波比小于1.3,幅度一致性小于0.025 dB,相位一致性小于0.2°。根据合成效率的计算公式,在幅相一致性影响不大的前提下,该系统的合成效率为88%。
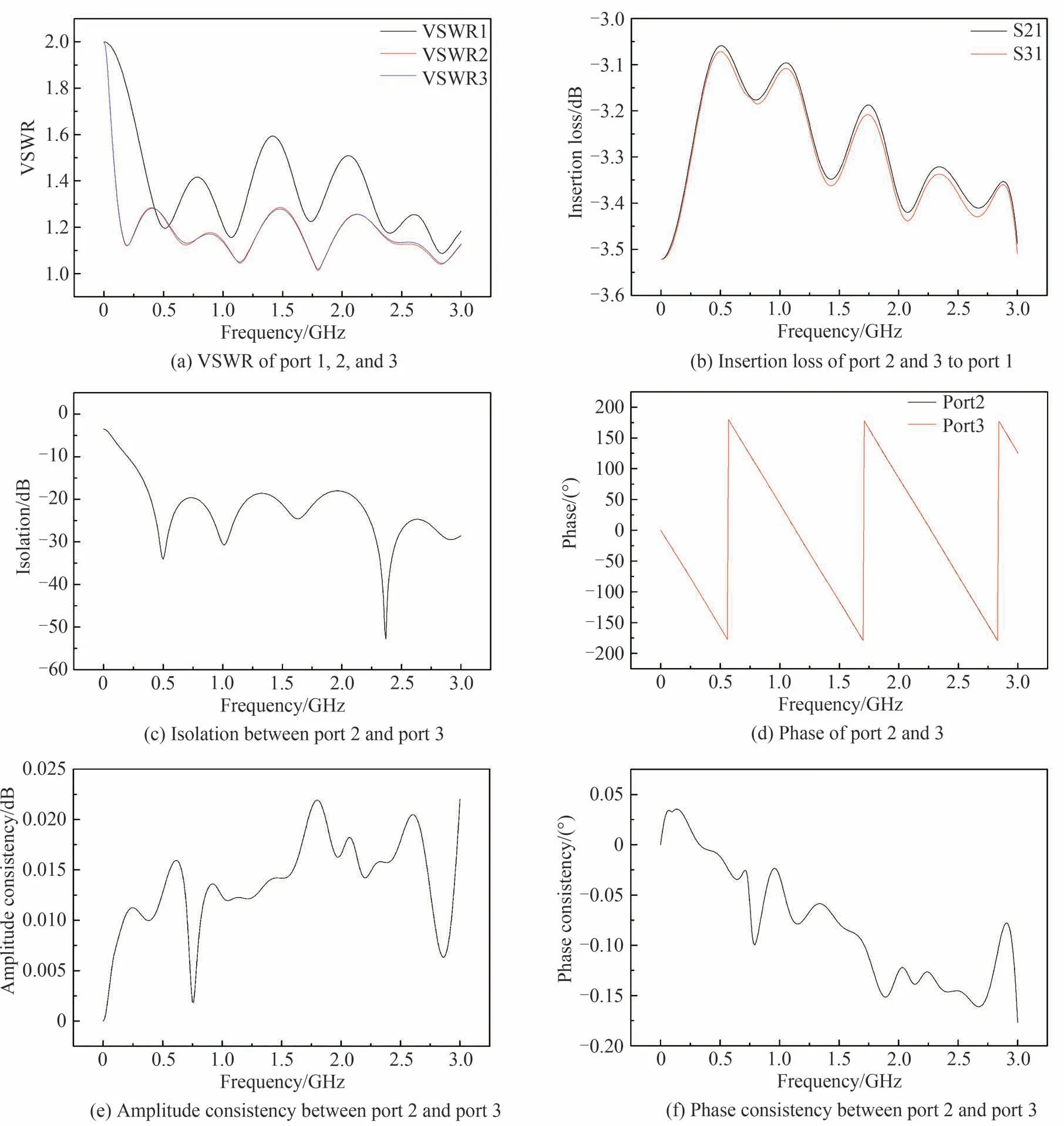
图6 二合一功率耦合电路的电磁模型仿真结果Fig.6 Electromagnetic model simulation results of the two-in-one power coupling circuit
将以上电路级联起来可以获得八路合一的功率合成电路,仿真结果如图7。由仿真结果可知,这种八合一功率耦合电路在工作频带内基本满足插入损耗小于1.836 dB,隔离度在13.54 dB 以上,输入端口驻波比小于2.42,输出端口驻波比小于1.37,幅度一致性小于0.6 dB,相位一致性小于2.5°。根据合成效率的计算公式,在幅相一致性影响不大的前提下,该系统的合成效率可以达到65.5%。
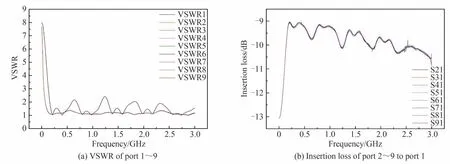
图7 八合一功率耦合电路的电磁模型仿真结果Fig.7 Electromagnetic model simulation results of the eight-in-one power coupling circuit
3 实验测试结果与分析
3.1 耦合电路加工与装配
为了满足功率合成系统的合成效率,必须控制电路中的损耗。实物电路选择罗杰斯ro5880 作为介质板材,它具有极低的损耗角正切,仅为0.000 9。与此同时它的相对介电常数为2.2,基板厚度为0.504 mm。为了兼顾高压脉冲与寄生参数的影响,隔离电阻选择0805 的封装的贴片电阻;耦合电路的输入输出端口使用SMA 头外接。图8 分别为二合一与八合一功率耦合电路的实物图。

图8 电路实物图Fig.8 Physical circuit diagram
3.2 矢量网络参数测试与分析
将两路耦合电路与八路耦合电路分别使用Agilent 公司的E5071A 型矢量网络分析仪进行端口矢量网络参数测试,结果如图9 和图10。
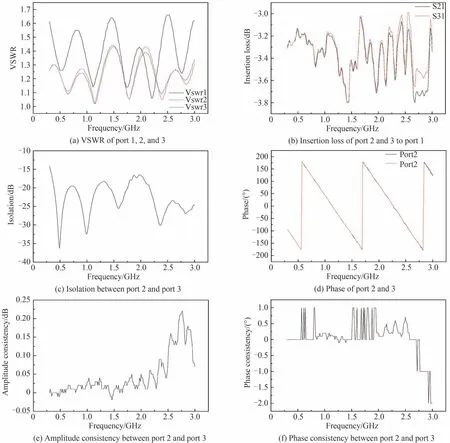
图9 二合一功率耦合电路的矢量网络参数测试结果Fig.9 Test results of vector network parameters of two-in-one power coupling circuit
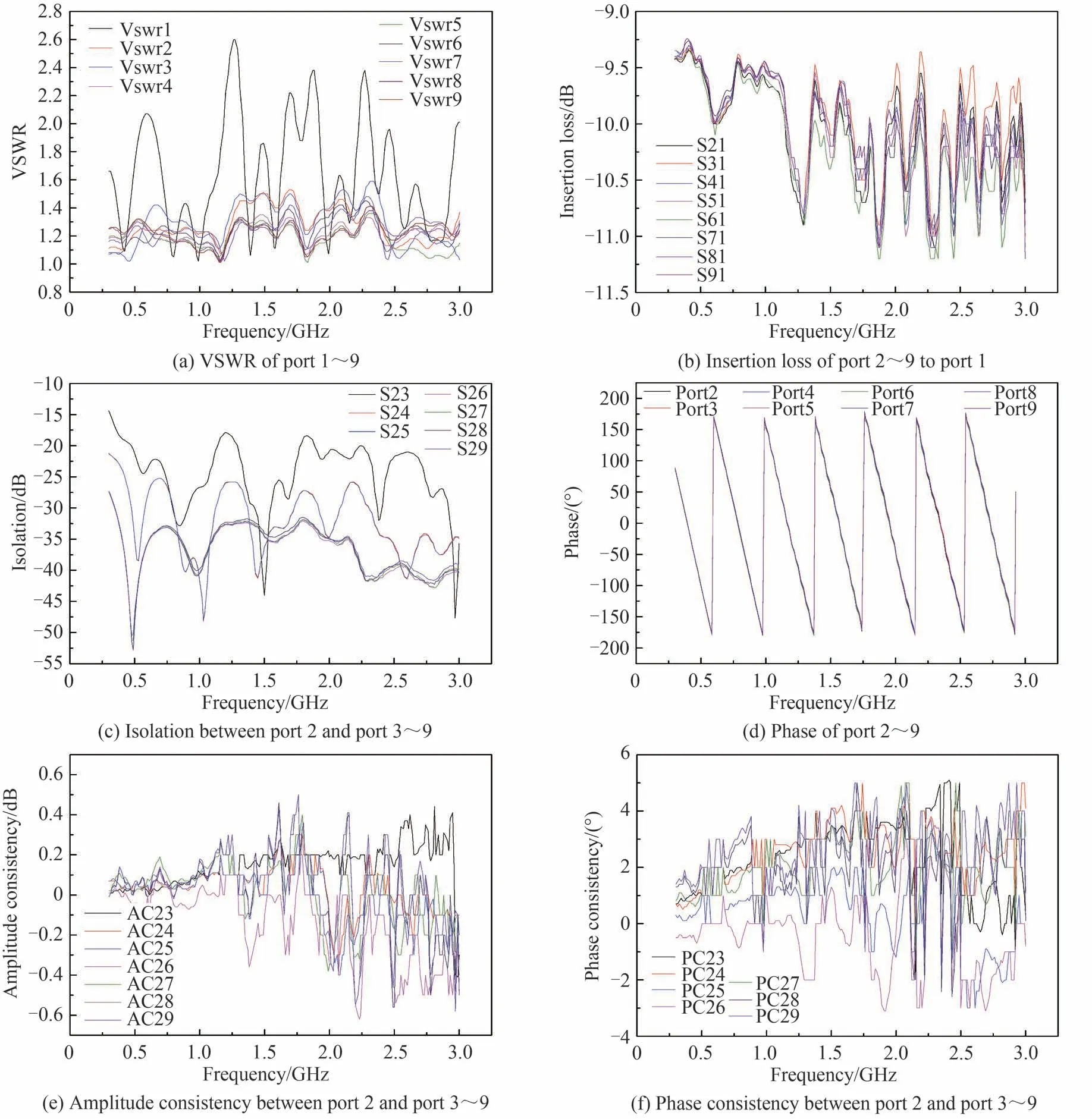
图10 八合一功率耦合电路的矢量网络参数测试结果Fig.10 Test results of vector network parameters of eight-in-one power coupling circuit
由实验结果可知,设计的两路耦合电路在工作频带内基本满足插入损耗小于0.78 dB,隔离度在15 dB以上,输入端口驻波比小于1.8,输出端口驻波比小于1.6,幅度一致性小于0.2 dB,相位一致性小于2°;设计的八路耦合电路在工作频带内基本满足插入损耗小于2.4 dB,隔离度在15 dB 以上,输入端口驻波比小于2.62,输出端口驻波比小于1.62,幅度一致性小于0.6 dB,相位一致性小于5°。根据合成效率的计算公式,在幅相一致性影响不大的前提下,两路耦合电路为83.5%,八路耦合电路的合成效率为58%。
将实验结果与仿真设计对比,发现二者有一定的偏差,实际电路较理论设计的个别指标下降,具体见表1(以两路耦合电路为例)。

表1 实验结果与仿真设计对比Table 1 Comparison between experimental results and simulation design
分析原因主要是因为:1)选择板材的介电常数在整个工作频带内是变化的,仿真时只考虑厂家给的经验值,这对整个电路的损耗有较大的影响;2)电路板制作时有一定的误差,微小的传输线宽度误差就会对驻波比造成比较大的影响;3)接插件本身的损耗也会使电路损耗加大,不同接口的焊接公差也会造成幅相一致性的恶化。以上问题导致实际耦合电路性能低于仿真设计。
3.3 合成效率测试与分析
利用八路高压脉冲合成实验测试耦合电路的合成效率。将同步控制电路、单路marx 高压脉冲生成电路与耦合电路逐级相连,同步控制电路负责调节各路脉冲的触发,使其可以在同一时刻完成功率耦合。所有脉冲均需要连接衰减器后再接入示波器,衰减比例为-60 dB。八路单路高压脉冲的参数如表2。图11和12 为示波器中测得的耦合脉冲的结果。经A1 与B1 脉冲耦合之后的输出脉冲幅度为-1.725 kV,脉宽为3.584 ns,脉冲前沿为621.9 ps;八路脉冲耦合之后的输出脉冲幅度为-3.229 kV,脉宽为2.645 ns,脉冲前沿为564.9 ps。
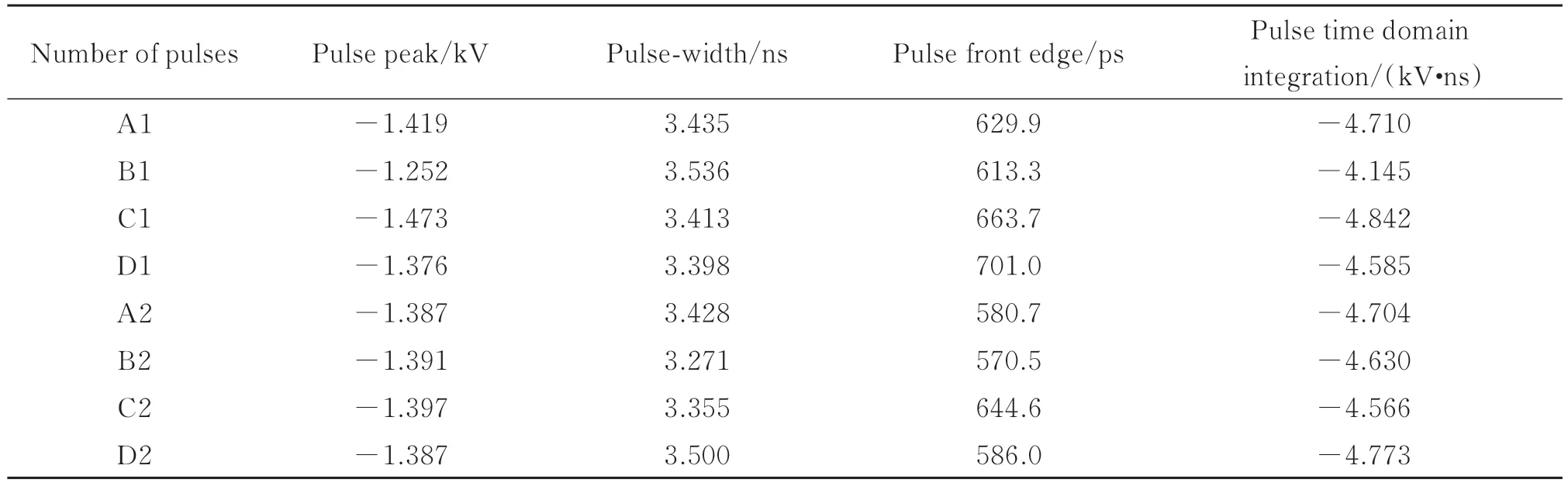
表2 八通道高压脉冲参数Table 2 Parameters of eight-channel high-voltage pulse
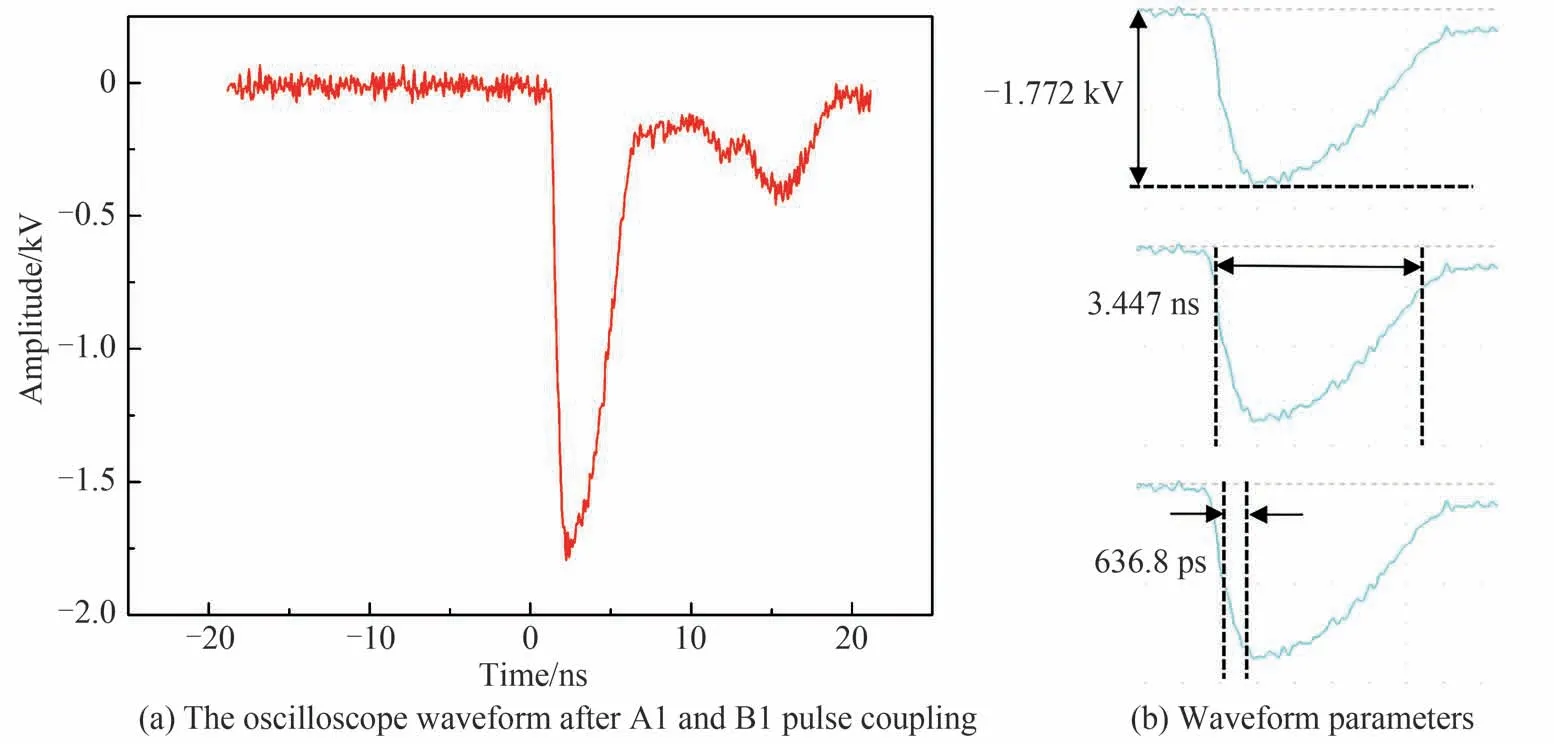
图11 两路耦合后的波形Fig.11 Waveform after coupling of two channels
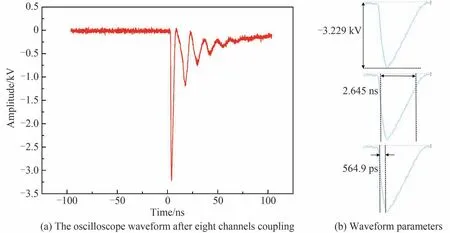
图12 八路耦合后的波形Fig.12 Waveform after coupling of eight channels
由此可分析得到,8 路峰值电压为1.3 kV 左右、脉冲宽度为3.5 ns、重复频率在100 kHz 的单路脉冲合成峰值功率超过3.2 kV 的高压脉冲。在该频谱下两路耦合效率为88%,八路耦合效率为68%。
3.4 分幅管驱动测试与分析
将八路高压脉冲耦合之后的高压脉冲输入到如图13 所示的20 mm 微带分幅管上,其内部的微通道板传输线宽20 mm、长95 mm、等效阻抗为6 Ω,如图14 所示。输出电压如图15。该脉冲幅值为1.433 kV、脉冲宽度为3.63 ns、脉冲前沿为747.3 ps,完全符合该分幅管输出电压须超过800 V 的设计要求。

图13 20 mm 微带分幅管系统装配测试Fig.13 Assembly and test of 20 mm microstrip framing tube system

图14 超宽画幅行波选通分幅相机的MCPFig.14 The MCP of the gated MCP framing camera with ultra wide format
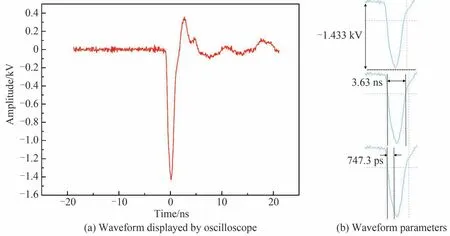
图15 分幅管输出波形Fig.15 The output waveform of the framing tube
增益是图像获取能力的一个重要标志性能。分幅相机增益主要由两部分因素所决定:分幅管自身的增益和选通脉冲的选通能力,而选通能力又与脉冲的峰值和脉宽有关。由于本文设计了一种基于脉冲功率合成的分幅相机选通脉冲源,所以该脉冲源输出脉冲将对分幅相机的增益产生影响。分析MCP 的增益时,可以将其看作离散打拿极倍增模型[29]。当一个光子在微通道内产生n次打拿极倍增,且二次电子倍增系数恒定,以一个电子从微通道子午面入射倍增为例分析微通道板的增益G,单个电子连续两次轰击微通道壁的间隔时间为t,轴向运动位移为z,其运动轨迹如图16。
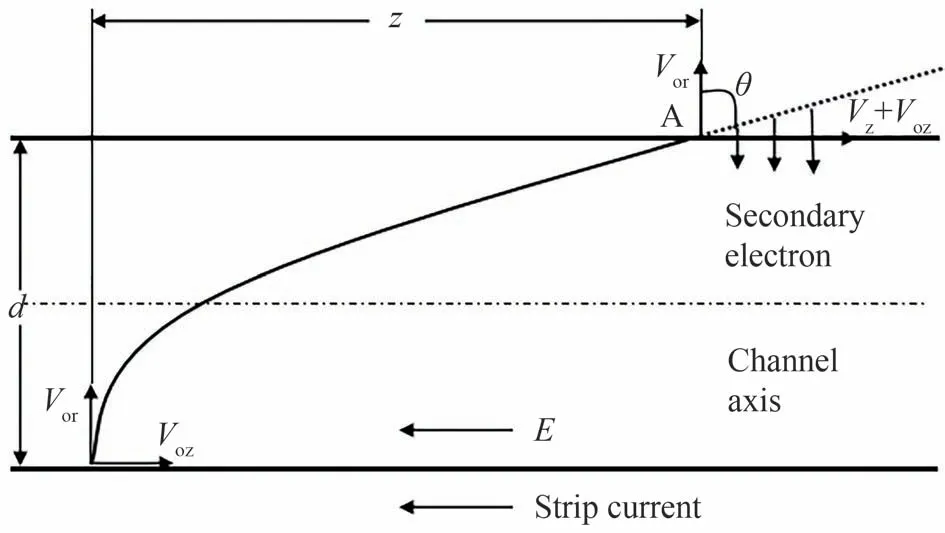
图16 电子入射到MCP 的运动轨迹Fig.16 The trajectory of the electron incident on MCP
只考虑微通道中的轴向电场E,如果微通道的直径为d,电子以抛物线的运动轨迹轰击微通道板,其轴向能量为eVoz,径向能量为eVor。如果轴向电场给电子的能量增量为eVz,结合牛顿力学知识,电子的轴向运动距离z可表示为
因此当轴向能量eVoz和径向能量eVor远小于能量增量eVz时,轴向位移只和eVor成反比。
为了得到电子的最佳入射角,需要假设二次电子平均径向出射能量eVor与电子轰击微通道壁的能量eVz有如下的关系
式中,β为比例常数,由此可得距离z为
如果通道长度和直径分别为L和d,二次电子的总体打拿极数有如下关系
已知电子的最佳入射角θ满足
由此MCP 的增益G可根据已知的电子打拿极倍增模型近似表示为
式中,δ1为第一级打拿极有效增益系数,δ为此外二次电子每级的有效倍增系数。经过多次实验测量发现可以用增益电压表示这两个增益系数,即
式中,VC为单位二次发射系数所需的最小电压,eVpk为光电子的入射能量,γ为MCP 的有效接收面积比,k为由二次电子发射的δ(VZ)函数曲线所给出的常数系数。因此MCP 的总的增益电压特性为
式中,各个常数不变时,增益与电压V呈正相关。由于微通道存在饱和效应,G不会随着V无限增大。当不考虑第一级倍增与后面打拿极倍增的差异,增益可以表示为
式中,V0为MCP 单位增益电压,θ为电子入射角,x(θ)为电子的初始入射深度。经过多次实验测得增益与电压有如下的关系
式中,C、n分别为增益的比例系数和指数系数。n取决于MCP 的性质,一般在7 到9 之间。根据微通道板增益与电压的函数关系,经功率合成之后的驱动脉冲峰值为3.2 kV 左右,较合成前的峰值在1.3 kV 的高压脉冲,增益将提升近1 000 倍,完全可以实现宽微带MCP 的大画幅成像功能。目前该耦合技术可以产生驱动脉冲供I-MCP1.0 型分幅相机使用。未来还可以通过调节八路脉冲的延迟对耦合脉冲进行整形。
4 结论
本文针对行波选通分幅相机超宽画幅驱动需求,基于宽带多节威尔金森脉冲功率合成方法,设计了一款高压驱动脉冲源。通过有限元分析方法,采用仿真软件对脉冲功率合成电路进行了仿真,系统分析了端口驻波比、插入损耗、端口隔离度以及幅相一致性等参数。根据仿真结果完成了脉冲功率合成电路研制,验证系统最终能够利用8 路峰值电压为1.3 kV 左右、脉冲宽度为3.5 ns 左右、脉冲前沿在600 ps 左右的单路脉冲合成峰值电压超过3.2 kV 的高压脉冲,脉冲宽度在3 ns 以内,脉冲前沿在600 ps 以内。脉冲频谱范围在300 MHz 到3 GHz 范围内的两路合成效率可以达到83.5%,特定频率下为88%,八路脉冲合成效率为58%,特定频率下为68%。通过该电路合成的高压脉冲可用于驱动宽20 mm、长95 mm、等效阻抗6 Ω 左右的MCP 实现选通成像,验证了基于宽带多节威尔金森电路实现脉冲功率合成,提高分幅相机驱动脉冲功率的可行性。目前基于本技术的高压驱动脉冲源已应用于I-MCP1.0 型分幅相机。

