基于GPU 加速的全源对最短路径并行算法

肖 汉，肖诗洋，李焕勤，周清雷

(1.郑州师范学院 信息科学与技术学院，河南 郑州 450044；2.东南大学 土木工程学院，江苏 南京 211189；3.郑州大学 计算机与人工智能学院，河南 郑州 450001)

图分析算法在许多领域具有重要应用价值，全源对最短路径算法是一种重要的图最短路径算法，在生物网络比对和路径推断、交通运输、运筹学、机器人动作规划、网络通信等领域有广泛的应用.但是，随着最短路径问题应用领域的数据规模迅速增长，数据结构日益复杂，数据处理时间过长，限制了其在实际中的应用[1].同时，全源对最短路径处理算法的计算量大，如何提高最短路径处理速度是当前图算法处理领域的研究热点之一[2].

当前，图形处理器（Graphics Processing Unit,GPU）的浮点运算处理能力是CPU 的10 倍以上，带宽是CPU 的5 倍，但成本和能耗远低于CPU，在许多方面具有很大的优势[3].架构方面，GPU 已经采用了统一计算架构单元，并实现了线程间通信和细粒度的任务分配，在通用计算领域GPU 已经显示出了强大的竞争力.统一计算设备架构（Compute Unified Device Architecture,CUDA）是一种非开放标准，仅适用于在NVIDIA 的GPU 硬件架构上运行，从而阻碍了CUDA 技术的推广.然而，随着基于GPU 的通用计算（General-Purpose computing on GPU,GPGPU）被人们广泛接受，业界已经针对GPGPU 制定了如开放式计算语言（Open Computing Language，OpenCL）的开放标准.设计适用在各种GPU 上且能够高效执行的基于OpenCL 的最短路径并行算法是一项有挑战性且非常有意义的工作[4-5].

本文利用OpenCL 架构实现了一种高效的基于CPU+GPU 的全源对最短路径并行算法（OCL_SP），解决了全源对最短路径算法在不同异构计算设备上快速处理大规模顶点集的问题.OCL_SP 并行算法在各种设备上表现出良好的可移植性.

1 相关研究

最短路径算法是许多复杂图算法的一个重要组成部分，普遍应用于科学研究和工程分析中.Jamour 等[6]将图表分解为双连通组件，图形中的所有点对最短路径的计算性能提高3.7 倍.Zhang等[7]采用方向共享、并行请求和路由点优化减少外部路由请求的数量，提出了一种能在外部路由请求中找到最佳路点集的贪心算法.Chandio 等[8]通过遵循批量同步并行参数预先计算路段的最短路径距离和速度约束，提出了一种基于云环境的实时GPS 轨迹的完全自适应地图匹配策略.Panomruttanarug[9]利用经典的路径规划方法找到最短的停车路径，并利用经验学习的能力跟踪设计路径.Hung 等[10]开发了一种分布式、并行且可扩展的最短路径算法消除网络中的冗余间接边缘.Gyongyosi[11]在量子中继器网络中以群体智能为基础，使用并行线程执行路由以通过纠缠梯度系数确定最短路径.闫春望等[12]提出了基于自动波理论的并行模糊神经网络最短路径算法，其迭代次数和收敛速度得到优化.李平等[13]采用双线程进行子网分割和拼接汇总得到最短路径，获得了2.07倍加速比.

Stpiczynski 等[14]通过基于Cilk 数组符号和内联函数的手动矢量化技术，实现了Belman-Ford 单源最短路径并行算法.Cabrera 等[15]提出了以稀疏矩阵-向量乘法的迭代为基础的单源最短路径算法，并行DBMS 系统获得了3.8 倍加速比.Maleki 等[16]采用具备16 个核心节点的共享和分布式存储器系统，设计了一种带状放松式Dijkstra 最短路径并行算法，取得了1.66 倍加速比.Chakaravarthy 等[17]采用边缘分类和方向优化，并提出负载平衡策略处理更高度的顶点，实现了基于CPU 集群平台的单源最短路径并行算法.孙文彬等[18]采用多粒度通讯的策略，实现了基于MPI 的Dijkstra 最短路径并行算法.

Liu 等[19]通过解决在稀疏矩阵-矩阵乘法中3个不规则性问题，最短路径问题在GPU 平台上获得了大约两倍加速比.李寅等[20]提出一种基于GPU架构的采样混合式全源对最短路径并行算法，算法采用BFS 遍历方法，能达到7.2 倍的加速比.叶颖诗等[21]设计实现了一种并行多标号Dijkstra 算法，获得了3.49 倍的加速比.Djidjev 等[22]提出了一种基于GPU 集群的Floyd-Warshall 最短路径并行算法，取得了一个数量级的性能提升.

Aridhi 等[23]采用并行方式求解原始图中每个子图上的最短路径，提出了一种基于MapReduce的解决道路网络中的最短路径问题.Gayathri 等[24]采用结合传递闭包属性和Dijkstra 单源最短路径算法中贪婪技术特征寻找到所有点对最短路径，在MapReduce 上设计了ex-FTCD 算法.何亚茹等[25]在基于神威平台的单个SW26010 处理器上，利用MPI 技术求解全源最短路径的Floyd 并行算法，取得了106 倍的最高加速比.

综上，最短路径并行算法研究有些以新型理论为基础提出新的最短路径算法，有些侧重对Dijkstra 等传统算法本身进行优化，有些基于CPU集群计算、CUDA 和GPU 集群等并行计算方式实现最短路径并行算法，有些则以大数据Hadoop 平台为基础设计最短路径高性能算法.可是，全源对最短路径问题采用多种算法多类平台系统进行性能评估报道目前较少.多数研究的加速效果不显著且均受限于一种算法或平台.本文将根据OpenCL框架特征和最短路径问题的特点，研究在GPU 加速下的最短路径算法和在不同并行计算平台下的算法移植性能.

2 最短路径算法分析

2.1 GPU 加速处理通用计算OpenCL 是一种开放的、免版税的标准，用于对个人计算机、服务器、移动设备和嵌入式平台中的各种处理器进行跨平台、并行编程.OpenCL 定义了具有模型层次结构的计算体系结构：平台模型、内存模型、执行模型和编程模型.OpenCL 平台由主机和连接到主机的计算设备组成[26].主机通常是CPU，OpenCL 设备可以是支持OpenCL 的设备，如CPU、GPU 和FPGA.OpenCL 设备执行内核，每个内核都是程序代码中的一个函数.内核以工作项为单位执行，工作项是并行执行的单位.整个工作项集合称为一个N-Dimensional Range (NDRange).共享其结果的工作项被组织成工作组的一个单元[27].

支持OpenCL 的计算设备由OpenCL 计算架构中的主机端系统统一管理和调度.当kernel 被主机端提交到设备端时，OpenCL 为任务并行处理定义了索引空间NDRange.执行内核的各个工作项的标识由其在NDRange 中的坐标表示.多个工作项可组织为工作组，提供了对NDRange 更粗粒度的划分，同一工作组中的多个工作项将在一个计算单元的不同处理单元上并发执行[28].

2.2 算法原理矩阵乘法求最短路径算法的核心思想是通过多次迭代计算求得点对间的最短距离.在该算法中是将原矩阵乘法中的“×”运算以“+”运算代替，“∑”运算以“min”运算代替[29].文中矩阵乘法运算内涵均按照此处说明进行.而重复平方法是对矩阵乘法的变形应用，重复平方法求最短路径是对每次计算得到的结果矩阵本身进行“×”运算[30].

在重复平方法最短路径算法处理的各个步骤中，建立有向图的带权邻接矩阵步骤、对邻接矩阵进行初始化步骤和建立邻接矩阵的镜像矩阵步骤的时间复杂度均为O(n2).利用邻接矩阵计算有向图各顶点间的最短路径步骤的时间复杂度为.因此，本文主要关注顶点间的最短路径阶段的并行性及优化.

2.3 可并行性分析存在于算法中的数据关联性与算法的可并行性好坏有关.若数据运算先后关联性越强，算法可并行性越低.反之，若数据运算先后关联性越弱，算法可并行性越高，并行化后算法的性能会越好.对加权有向图的重复平方法最短路径算法的可并行性分析如下，如图1 所示.

图1 加权有向图Fig.1 Weighted digraph

图1 中有权邻接矩阵L(1)如式(1)所示.按照重复平方法计算，则有权邻接矩阵L(2)如式(2)所示（“ ⊕”符号代表两个矩阵进行重复平方法运算）.在计算L(2)的过程中，发现L(2)中一个任意元素的计算和其余元素的计算过程相互无关，不存在依赖性.即在L(2)中计算某个元素值时，可对其余元素值同时进行运算.结合OpenCL 模型的特性，在工作项中进行每个元素的计算，这样，L(2)中每个元素的结果将由工作项计算得出.如果计算完矩阵中的每个元素，则本轮结束计算，如果需要迭代，则重复上面的过程.

3 最短路径并行算法的设计和优化

3.1 并行算法描述设有相同邻接矩阵A、B，邻接矩阵A、B中的子矩阵分别存储于数组As和数组Bs中，每次计算之后的最小值由v保存，矩阵C存放的是完成计算后点对间最短路径长度数据.重复平方法最短路径并行算法描述见算法1.

算法1 SIMT 模型上的重复平方法最短路径并行算法

矩阵乘法是重复平方法最短路径并行算法的核心运算.每一个工作组负责矩阵C中v的计算，每一个工作项计算比较得出v的最小元素值.每个工作组中的工作项被划分成为Bsize×Bsize的正方形计算工作项，与正方形计算工作项对应的矩阵A、B中的数据就是需要进行计算的源数据.在每次进行运算前，将源数据存入本地存储器As和Bs中.在每个工作组内进行计算时，工作组ID 不变，工作项ID 也不变，每循环一次需要更新一次本地数组As和Bs中存放的数据.当As和Bs中数据更新完毕，对于As中的每一行元素、Bs中的每一列元素，由每个工作项负责数组As和数组Bs中对应元素的求和、取最小值运算，并将取得的最小值存入v中.当该正方形中的元素全部读取计算完毕，则读取该计算条带中的下一个正方形区域源数据，直到每个工作组中的元素全部读取计算结束.工作组中的正方形计算区域每次移动的步长为Bsize.当工作组中所有元素读取计算完毕时，v中保存的就是这些矩阵中对应元素和的最小值.直到所有工作组中的所有线程全部计算结束，把最终得到的结果再从本地存储器写回全局存储器.

3.2 算法并行化思路OCL_SP 算法具体执行步骤如下.

步骤 1根据顶点数，在主机端初始化邻接矩阵A并保存.

步骤 2初始化OpenCL 平台.

步骤 3命令序列对象通过上下文及指定设备创建.在设备和上下文之间通过clCreateCommandQueue建立逻辑连接，以协调内核计算.

步骤 4输入源文件并创建、编译程序对象.依据在上下文中的设备特性，通过运行时编译构建程序对象，OCL_SP 并行算法具备了较强的可移植性.

步骤 5设置OpenCL 内存对象和传输数据.首先创建buffer 存储器对象，接着将存储器的访问任务加载到命令队列中，最后利用clCreateBuffer将邻接矩阵A、B隐式的从主机写入到设备的全局内存中.

步骤 6构建kernel 对象.利用clCreateKernel将内核函数与参数封装到指定的kernel 对象中.

步骤 7为kernel 对象设置参数传递.

步骤 8构建顶点数目满足的条件，创建内核函数，调度内核执行.

步骤 9循环调用内核函数对数据的处理，计算点对间的最短路径距离值.

步骤 10在设备端中完成运算任务后，将结果传输到主机端存储器，释放设备端内存空间；并将最终计算结果保存至相应文件.

3.3 并行算法的加速策略

3.3.1 理论设计 设计重复平方法最短路径并行算法时，矩阵乘法采用了混合划分法实现.混合划分法由带状划分法和棋盘划分法组成，在工作空间NDRange 中采取的是带状划分法，在每个工作组内采取的是棋盘划分法.

工作空间中的带状划分法如图2 所示，其中一个工作组对应矩阵A和 矩阵B中一对计算条带的运算，运算完成后的结果放在矩阵C的对应位置上.在矩阵A中阴影区域计算条带的高度为Bsize，矩阵B中阴影区域计算条带的宽度为Bsize.在每个计算条带中，再对数据元素进行棋盘式的划分.每次计算时，块坐标不变，但是每次读取数据的步长按照Bsize增加，以更新将要计算的数据.计算条带内划分方法如图3 所示.

图2 NDRange 带状划分图Fig.2 NDRange banded partition diagram

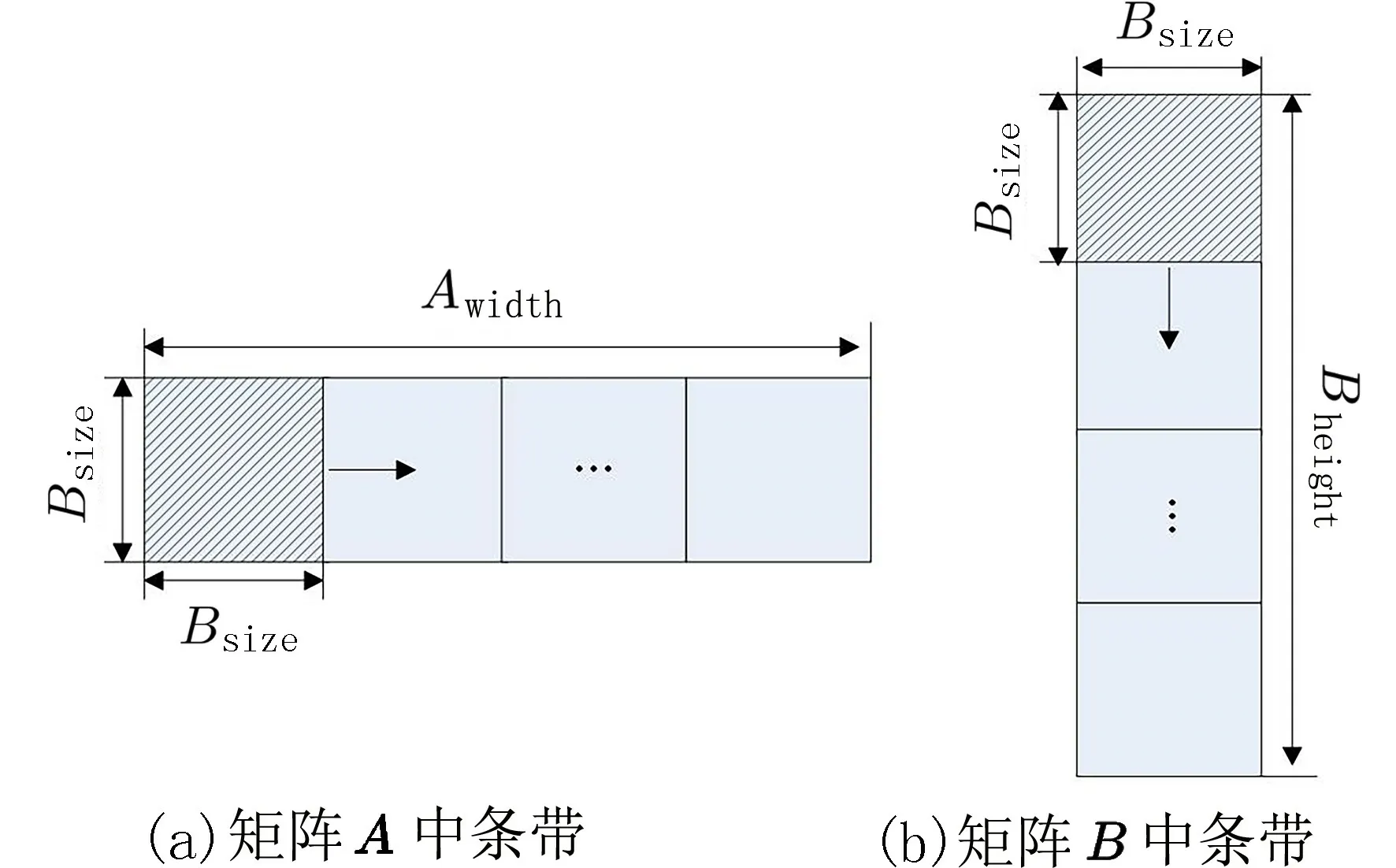
图3 工作组内棋盘划分图Fig.3 Chessboard division diagram in the working group

在进行矩阵乘法运算时，工作组每次加载一个计算条带.由于计算条带宽度为Bsize，所以每次进行迭代的步长是Bsize.根据带状划分的方法，矩阵A从全局存储器完全被加载到本地存储器，需要被工作组内的本地存储器读取Bwidth/Bsize次 .而和矩阵A进行矩阵乘法运算的矩阵B需要被工作组内的本地存储器读取的次数是Aheight/Bsize次，这样的数据读取方式大量减少了直接从全局存储器读取数据的延迟时间.工作组内按照棋盘划分法设计矩阵乘法.每个工作项负责读取矩阵A中的一行元素和矩阵B中的一列元素，计算得出矩阵C中对应的元素值，并储存在全局存储器中.

对于每一个工作组，都需要由A的一行元素和B的一列元素进行比较计算之后才能得到最终结果，如图4 所示.矩阵A中高度为Bsize长度为Awidth的矩形代表一个工作组，U和U′分别代表读取到本地存储器As和Bs的正方形区域源数据.每个工作组内的操作过程如下：

图4 矩阵乘法的分块计算Fig.4 Block calculation of matrix multiplication

步骤 1把U和U′从全局存储器中读出，放入本地存储器As和Bs中 .在边长为Bsize的正方形计算区域中，一个工作项对应加载一对元素，然后利用矩阵乘法计算比较得出最小的元素值，并存入v.

步骤 2进行for 循环，以边长Bsize为步长进行迭代，更新As和Bs中保存的数据.重复步骤1 直到读取完该计算条带A的每行元素和相应计算条带B的每列元素.

步骤 3在最后一次内层for 循环中，W和W′被放入As和Bs中，在最后一轮比较运算中所有工作项将所有计算任务完成后，每个工作项计算比较得出的最终结果保存在v.相应在图4(c)中，计算得出了图中的块标号为(0,0)的块中的数据.

步骤 4对于矩阵C中的每个小块，都进行上述相同的操作，直到全部计算结束，矩阵C中保存的就是该轮计算得出的结果.

3.3.2 kernel 函数的配置设计 整个邻接矩阵A依据互不重叠的划分原则，可以被分割为若干个计算条带.计算条带作为基本处理单位，存在于计算条带中的大量矩阵乘法计算可交给OpenCL 工作组和工作项处理.文中采用二维索引空间来设计，从数据角度来讲，二维索引空间在x、y方向上的维度均为D，工作组在x、y方向上的维度均为Bsize，工作空间在方向x、y方向上工作项总量均为base×Bsize.因此，内核函数的网格配置如下：

3.4 优化设计

3.4.1 本地内存的设计 GPU 计算性能常受制于存储器速度.由于运算速度与显存带宽间的不平衡，OpenCL 定义了多层存储器体系结构.文中依据算法特征将存储器的合理分配和优化运用于计算流程中的访存方式和数据传输.在重复平方法最短路径算法的矩阵乘法运算中，邻接矩阵An×n、Bn×n中的每一个数据都需要被重复读取n次.如果将计算条带放在具有400～800 个时钟周期读写延迟的全局存储器中，将大大降低并行数据访问速率.通过引入仅具有1（无bank 冲突）～16 个时钟周期（发生16 路bank 冲突）读写延迟的本地存储器，将需要大量重用的计算条带数据在计算前预置在本地内存As和Bs中.这样既能方便地在工作项间进行通信，也使工作项的访存速度更快从而大量的全局存储器延迟被透明地隐藏起来.因此，并行算法中采用静态分配方式在内核函数中对As和Bs分配本地存储器空间：

同时，在不同的本地存储器 bank 中存储了每条计算条带中的数据，保证了在同一个warp 中相邻的一组32 个访问工作项与bank 是一一对应，避免了bank 冲突，有效提高了运算速度.

3.4.2 NDRange 优化 计算单元应该保持较高的占用率.因为工作项指令在OpenCL 中是顺序执行，隐藏延迟的有效方法就是在一个warp 繁忙时执行其他warp.若存在足够多的工作组数量，就可避免因warp 块填充不足导致OpenCL 系统的计算资源浪费.一个工作组中保持的工作项最好是32的倍数.由于有向图的顶点数是变化的，工作组和工作组中的工作项数应该根据所占用的寄存器空间及本地存储器空间动态分配，以达到最佳效率.针对OpenCL 加速的全源对最短路径图算法，当有向图顶点数为5 000 时，不同工作组维度下，算法运算时间比较如表1 所示.从表1 中可见，当工作组维度为16×16 时，全源对最短路径并行算法的运算时间最短.

表1 算法运算时间比较Tab.1 Compare the operation times of algorithm

3.5 其他优化方案为了便于各种并行化方案的性能比较，本文分别在OpenMP 和CUDA 并行计算体系结构上实现了一种符合2.2 节最短路径算法原理的并行算法.

3.5.1 基于OpenMP 的最短路径并行算法（OMP_SP）在Windows 系统中，使用OpenMP 内置的Microsoft Visual Studio.Net 2017 编译器，在项目的Microsoft.Cpp.x64.user 属性页中设置‘C/C++→Language→OpenMP Support’为“是(/OpenMP)”，在Visual Studio.net 2017 中打开OpenMP 编译选项.然后将选项“C/C++→Gode Generation→Runtime Library”更改为“多线程调试(/mtd)”.

OpenMP 是一种粗粒度并行.根据CPU 核心的数量，并行块通过omp_set_num_thread (thread)启用子线程进行并行执行.主线程执行OMP_SP并行计算系统，当遇到位于构造初始邻接矩阵L(1)、保存L(1)到A和B、矩阵乘法等函数之前的编译引导指令#pragma omp for 时，将对后面的循环体进行多线程分解.每个线程并行处理结果矩阵的一个元素.

3.5.2 基于CUDA 的最短路径并行算法（CUDA_SP）CUDA 是一个细粒度的平行.将最短路径算法可并行的矩阵乘法功能部分划分为一个任务.该任务由相应的global 函数处理.在算法运行过程中，global 函数与网格一一对应，网格将任务分配给线程块，线程块将任务重新分配给线程进行处理.主机端调用global 函数，在GPU 端的多个计算处理单元中进行并行处理.

4 实验结果及分析

4.1 测试环境和数据记录选择单精度数据类型实现是因为它的准确性，而且GPU 针对现代计算机在单精度浮点运算上进行了高度优化.

用OpenCL C 语言开发了全源对最短路径并行算法的核心源代码.该并行算法由两部分构成，在主机上执行主程序部分，另外内核程序部分是在OpenCL 设备上执行.核心代码实现了矩阵乘法运算.

实验工作是在CPU/GPU 异构混合并行计算平台上进行.硬件环境参数如下：平台1：CPU 为AMD Ryzen5 1600X 3.6 GHz 六核；系统内存容量为24 GB；显卡采用NVIDIA Geforce GTX 1070 GPU.GTX 1070 拥有1 920 个CUDA 核，核心频率是1 506 MHz.搭配8 GB GDDR5 显存容量，显存位宽256 位.平台2：CPU 为AMD Ryzen5 1600X 3.6 GHz 六核；系统内存容量为24 GB；显卡采用AMD Radeon RX 570 GPU.Radeon RX 570 拥有2 048 个核心，核心频率是1 168 MHz.搭配8 GB GDDR5 显存容量，显存位宽256 位.

软件平台：采用Microsoft Windows 10 64 位为操作系统；Microsoft Visual Studio.Net 2017 为集成开发环境；CUDA Toolkit 10.0 为系统编译环境并支持OpenCL 1.2 标准.

有向图的顶点集大小n分别设为10、50、200、300、1 400、2 000、5 000、8 920 和10 000，从小规模顶点集到大规模顶点集都均匀覆盖，有利于准确反映全源对最短路径并行算法的性能可扩展性.rand()随机数函数的随机数种子采用n可生成一组随机数，生成具有代表的节点数量为10、50、200、300、1 400、2 000、5 000、8 920 和10 000 的图，并构成相应的邻接矩阵A.邻接矩阵是使用二维数组模拟线性代数中矩阵的结构.此种数据结构所使用的储存空间较大，但其使用较为便捷.根据重复平方法最短路径算法的原理，分别基于OpenMP 和CUDA 并行计算架构实现了最短路径并行算法.

测试并记录CPU_SP 系统（平台1 测试），OMP_SP 系统（平台1 测试）、CUDA_SP 系统、基于AMD GPU 的OCL_SP 系统和基于NVIDIA GPU的OCL_SP 系统的处理时间，如表2 所示.从表2可以看出，随着顶点数的增大，最短路径算法的执行时间越来越长.基于GPU 的最短路径算法运行时间要比CPU_SP 和OMP_SP 算法的运行时间少的多，而OMP_SP 算法运行时间要比CPU_SP 算法的运行时间更短.

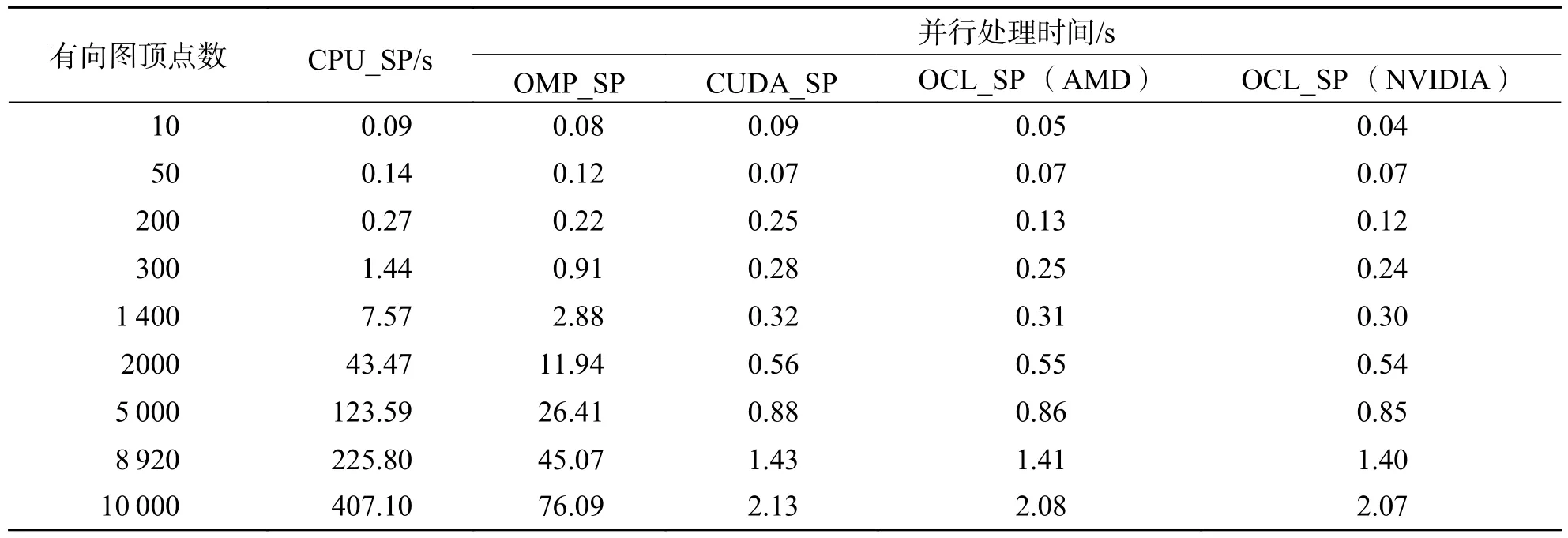
表2 不同计算平台下最短路径算法执行时间Tab.2 The shortest path algorithm execution time under different computing platforms

用加速比作为加速效果的衡量标准，可以验证各种架构下并行算法的效率.加速比定义如下：

式中：Ts是指算法运行在单线程CPU 平台上的时间，Tp是指算法运行在多线程CPU 或CPU+GPU协同计算平台上的时间.

OMP_SP 并行算法执行时间Tpo与基于NVIDIA GPU 的OCL_SP 并行算法执行时间Tpnc的比值为相对加速比R1，定义为：

CUDA_SP 并行算法执行时间Tpc与基于NVIDIA GPU 的OCL_SP 并行算法Tpnc执行时间的比值为相对加速比R2，定义为：

式中：在CPU 和GPU 上OpenCL 内核的计算时间之和为Tk，CPU 和GPU 之间数据传输时间之和为Th，系统初始化时间之和为To.

加速比可用于评估并行算法相比CPU 串行算法的性能提升.相对加速比R1可用于评估基于NVIDIA GPU 的OCL_SP 并行算法相比OMP_SP并行算法的性能提升.相对加速比R2可用于评估基于NVIDIA GPU 的OCL_SP 并行算法相比CUDA_SP 并行算法的性能提升.根据表2 可得算法加速比情况，如表3 所示.

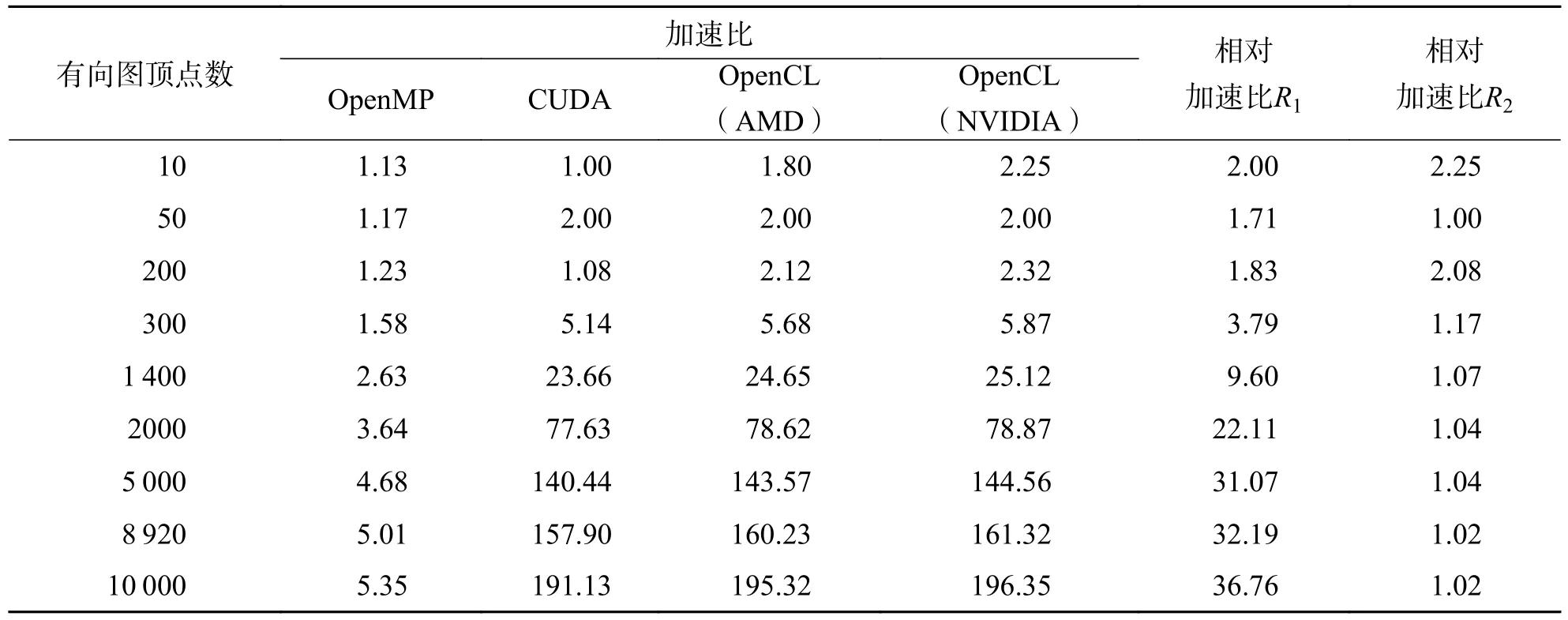
表3 不同计算平台下最短路径并行算法性能对比Tab.3 Performance comparison of parallel algorithm of shortest path on different computing platforms

4.2 并行算法性能分析

4.2.1 系统性能瓶颈 OCL_SP 并行算法需要n×n×log(n-1)×2次右邻接矩阵的存储器读取操作，以及n×n×log(n-1)次输出矩阵的存储器写入操作.顶点集大小为n=10 000，每个数据占用2 B的存储空间.因此，存储器访问的数据总量约为6 GB.除以设备上内核执行所用时间0.028 s.系统实际获得的带宽约为214.29 Gb/s，接近GeForce GTX1070 显存的理论带宽.由此可见，全局存储器的带宽限制了OCL_SP 并行算法效率的进一步提高.因此，OCL_SP 并行算法的性能瓶颈是显示内存带宽.

4.2.2 不同架构下最短路径算法处理时间分析 根据表2 显示，对不同顶点数的加权有向图进行全源对最短路径处理将在 4 种计算平台上进行.在顶点数一样时，最短路径算法在不同并行计算架构下的处理时间相对串行处理时间均有不同程度缩减，即获得了性能提升效果.如：对于顶点数为10 000的最短路径串行运算时间为407.10 s，OMP_SP 算法运算时间缩短为76.09 s，CUDA_SP 算法运算时间则大幅缩减为2.13 s，而基于OpenCL 并行计算平台上则保持在2.07 s 左右的低运算时间.

设n为加权有向图G(V,E)的顶点数，c为多核CPU 核心数，OMP_SP 并行算法的时间复杂度为在相同顶点数下，存在OMP_SP 并行算法的时间复杂度因此，从表2 可以看出，OMP_SP 并行算法相比CPU_SP 串行算法的处理时间有明显降低.同时可以看出，设置线程数c恒定时，随着顶点数n的增大，OMP_SP并行算法的时间复杂度也随之增加.每一个CPU线程负责处理的邻接矩阵乘的数据规模也随之增大，OMP_SP 并行算法处理时间也越来越长，基本符合线性增长的趋势.

当邻接矩阵的计算规模较小时，在GPU 算法中启动的工作项计算负荷不足，系统在调度方面有较大时间开销.此时GPU 算法与CPU 算法的处理时间接近，GPU 并行计算的优势没有展现.随着邻接矩阵的计算规模增大，每个工作项计算负荷也逐渐提高，而系统调度的时间占比降低，GPU 并行计算占比上升，速度提升明显.

4.2.3 并行计算架构下最短路径算法加速效果对比分析 设n为加权有向图G(V,E) 的顶点数，u为GPU 启动的工作项的数据量，CUDA_SP 和OCL_SP 并行算法的时间复杂度为由于在GPU 中可以维护大量的活动线程和工作项，即u≫c.因此，在相同顶点数下，存在CUDA_SP和OCL_SP 并行算法的时间复杂度从表3 可以看出，当有向图的顶点集合较小时，OMP_SP 并行算法与基于GPU 的最短路径并行算法的加速效果相当.分析其原因，OpenMP的并行开销要小于GPU.由于OMP_SP 并行算法是在CPU 端执行，不同于GPU 并行算法需要在CPU 与GPU 之间进行数据传递.而且OpenMP 启动的线程少，线程维护成本低.当顶点集合逐步增大时，OMP_SP 并行算法的加速效果始终维持在一个较低的水平，而GPU 并行算法的加速效果更好.这主要是由于OMP_SP 并行算法需要操作系统将线程调度到对应数目的CPU 核心上执行，多核CPU 的核心数是有限的.反观计算资源充裕的GPU 可以创建足够的工作项以满足大规模数据的并行处理.同时，随着顶点数n的增大，CUDA_SP和OCL_SP 并行算法的时间复杂度也随之增加，每一个线程或工作项负责处理的邻接矩阵乘的数据量也随之增大.从表2 可以看出，CUDA_SP 和OCL_SP 并行算法处理时间也适当的增长.

从表3 可以看出，当顶点集合规模较小时，GPU 加速的最短路径并行算法性能改善并不明显.当顶点集合规模较大时，CUDA_SP 和OCL_SP 并行算法的性能提升较为显著，在3 种不同并行计算架构下有效的性能收益明显.当顶点集合n=10 000时，基于NIVIDA GPU 的OCL_SP 并行算法的加速比更达到了196.35 倍.然而，当顶点集合规模n＞5 000以后，GPU 加速的最短路径算法加速比曲线呈现一种缓慢上升的过程.说明在顶点集规模较大的情况下，系统已不能获得更快速的性能提高.主要原因是GPU 的计算资源接近饱和.主机和设备间的数据传输时间占比越来越大，并行计算时间的缩短已对加速比贡献甚微.

采用离线编译内核读写数据文件方式的OCL_SP 并行算法，相比采用在线编译内核读写数据文件方式的CUDA_SP 并行算法减少了应用初始化时间.如表3 所示，在同等数据集规模下，OCL_SP 并行算法的运算耗时更少，与CUDA_SP并行算法性能相比略有提升，最大获得了2.25 倍加速比.OCL_SP 并行算法性能与OMP_SP 并行算法性能相比则有很大的提高，最大获得了36.76 倍加速比.

将本文提出的OCL_SP 算法的整体加速效果与文献[25]进行对比.由于其他文献大多是利用最短路径算法进行各种应用研究，很少专门针对全源对最短路径算法进行加速效果的研究.因此，无法直接进行加速效果的对比.根据文献[25]中提供的测试数据，当每个核组开启64 个从核时，经过数组划分优化后的全源最短路径并行算法获得了106倍加速比.而根据表3 的测试结果可以看到，OCL_SP 并行算法最高获得了196.35 倍加速比.因此，OCL_SP 并行算法相比文献[25]中的算法取得了更好的加速性能.

4.2.4 OCL_SP 并行算法跨平台性分析 源码级别的算法可移植性不仅要求在不同的平台上源码可以成功地编译和运行，同时还需要算法保持相当的性能.CUDA_SP 并行算法受到硬件平台的限制，表3 中数据显示，在多种硬件平台上OCL_SP 并行算法具备了最大程度的兼容性和可移植性.

5 结束语

针对全源对最短路径图算法中数据量大、运算量大和高计算密集度等问题，本文设计了采用GPU 加速的最短路径并行算法.分别从算法可并行性分析、算法描述和框架的设计、矩阵乘法的加速策略以及存储器优化策略等方面进行了阐述.实验结果表明，OCL_SP 并行算法分别与CPU_SP 串行算法、OMP_SP 并行算法和CUDA_SP 并行算法的性能相比，取得了196.35、36.76 和2.25 倍的加速比，不但实现了高性能，而且在不同GPU 计算平台间实现了性能移植.拥有大量计算单元和强大计算能力的GPU，为图论有关问题的快速求解提供了一种廉价而高效的计算平台，为高效地大规模数值计算进行了有益探索.在下面的工作中，我们将把多CPU 与多GPU 构成的异构计算平台作为并行计算模式，采用并行I/O 技术，以达到更大规模数据集对计算能力的要求.