Invariant manifold growth formula in cylindrical coordinates and its application for magnetically confined fusion

Wenyin WEI(魏文崟) and Yunfeng LIANG(梁云峰)

1 Institute of Plasma Physics,Hefei Institutes of Physical Science,Chinese Academy of Sciences,Hefei 230031,People’s Republic of China

2 University of Science and Technology of China,Hefei 230026,People’s Republic of China

3 Forschungszentrum Jülich GmbH,Institut für Energie- und Klimaforschung-Plasmaphysik,Jülich D-52425,Germany

Abstract For three-dimensional vector fields,the governing formula of invariant manifolds grown from a hyperbolic cycle is given in cylindrical coordinates.The initial growth directions depend on the Jacobians of Poincaré map on that cycle,for which an evolution formula is deduced to reveal the relationship among Jacobians of different Poincaré sections.The evolution formula also applies to cycles in arbitrary finite n-dimensional autonomous continuous-time dynamical systems.Non-Möbiusian/Möbiusian saddle cycles and a dummy X-cycle are constructed analytically as demonstration.A real-world numeric example of analyzing a magnetic field timeslice on EAST is presented.

Keywords: magnetic topology,tokamak,invariant manifold

1.Introduction

In the tokamak community,the magnetic topology is,most of the time,assumed to be nested flux surfaces,e.g.in Grad-Shafranov equation,EFIT,VMEC,etc.Based on this assumption,people have established a dedicated theory [1]of magnetic coordinates in which all magnetic field lines on a flux surface are straight.Nevertheless,the threedimensional(3D) effect is ubiquitous in real-world fusion experiments since any facility in fusion machines,except the central solenoid and poloidal field coils,is 3D.For example,the toroidal field coils exhibit a ripple effect,the microwave and radio-frequency wave heating methods impose their distinctive localized distribution pattern of the induced current,and the neutral beam injection has an obvious non-axisymmetric current effect.Furthermore,most instability modes of plasma,such as the tearing mode and sawtooth mode,imply a significant 3D topology change of the magnetic field.The 3D effect is unavoidable in the magnetically confined fusion research,thereby requiring a deeper comprehension on the global field structure.

An enormous amount of fusion research has attempted to stimulate a chaotic field layer at the plasma boundary by either resonant magnetic perturbation(RMP) coils [2-4] or other means [5] to mitigate destructive type-I edge localized modes(ELMs).The theoretical basis was established in 1983 by Cary and Littlejohn [6] to estimate how wide the island chains are when an axisymmetric magnetic field is perturbed by a non-axisymmetric one,after which hundreds of researchers implement RMP coils to mitigate and suppress ELMs [7,8].The method is called magnetic spectrum analysis nowadays,heavily relying on Fourier transform of the radial component of the perturbation field,which is a linear operation in functional spaces.Therefore the utility of magnetic spectrum analysis is limited inside the plasma and becomes less and less accurate as the perturbation is strengthened,because Fourier transform is merely a linearoperation and not capable of explaining the nonlinear behaviour.

Table 1.Denotations.

With the aid of modern dynamical system theory,the structure of a 3D vector field can be comprehended and analyzed in terms of invariant manifolds [9,10].Various numerical methods have been developed to grow them[11-16].Kuznetsov and Meijer systematically investigated the bifurcation behaviour of 1D and 2D maps when their parameters change [17,18],presenting diverse analytic and numerical methods to study maps.However,the methods taken by mathematicians are too general to capture the essence of a 3D vector field,leaving the analysis as complicated as before.

Since the magnetic field dominates the plasma transport in magnetically confined fusion machines,the evidence of transversely intersecting invariant manifolds shall be easy to observe,which is a signature of chaos.The invariant manifolds are essential to determine the chaotic field regions,which induce a mixing effect inside the plasma.The plasma edge is not suitable to be characterized by a single closed surface when the 3D effect is strong,for which it is proposed to use the notion of invariant manifolds of outmost saddle cycle(s).In fact,it has been observed in some existing simulation [19-22] and experiment results.On EAST,the helical current filaments induced by the lower hybrid wave heating impacted the plasma edge topology and caused an evident splitting of strike points in experiments [5].

If RMP coils are imposed to suppress ELMs in tokamaks,the heat flux pattern at the divertor exhibits a complex toroidally asymmetric distribution,which poses challenges to ITER and DEMO divertor designs [23].Simulation results demonstrate that the divertor plasma regions with connection to the bulk plasma are dragged further outside when the asymmetry is intensified [24,25].The field line connection length and the magnetic footprint(how deep the field lines penetrate into the bulk plasma)distribution at the divertor are usually ribbon-like.The RMP does mitigate or even suppress the ELMs,otherwise which can cause intolerable transient particle and heat flux.On the other hand,significant heat fluxes may arise far from the strike point originally designed for axisymmetric cases [26],possibly damaging the fragile parts of the divertor.Moreover,it remains unknown whether the total heat flux leaked from the bulk plasma is reinforced by the perturbation.

Previous research has attempted to draw the two transversely intersecting manifolds of hyperbolic cycles for 3D toroidal vector fields.Ottino from the community of fluid mechanics[27],Roeder,Rapoport,and Evans from the fusion community [28,29] have drawn up the relevant figures.Abdullaev has deduced an approximate(to first order in ∊because Poincaré integral is used)analytic implicit expression of the invariant manifolds of the outmost X-cycle when a single-null configuration is perturbed [30].This paper carries forward the research and directly deduce the intrinsic analytic formula of the invariant manifolds of hyperbolic cycles without need for approximation.

Section 2 explains the definitions and denotations used in this paper.The theory skeleton of this paper is put in section 3,while the detailed proofs are put in appendix A.Section 4 offers intuitive examples to help understand the theory.Non-Möbiusian/Möbiusian saddle cycles and a dummy X-cycle model are constructed analytically.A realworld numeric example of analyzing a magnetic field timeslice on EAST is presented subsequently.Section 5.1 and appendix B give comparisons with others’works.Section 5.2 is the conclusion.

2.Definitions and notations

Vector fields are presumed to be at least once continuously differentiable,i.e.of classC1.Although a vector field is denoted by B,it is worth emphasizing that it does not need to be divergence-free in this paper.

The flow X(x0,t) induced by the field B and the corresponding flow Xpol(x0,φs,φe) in cylindrical coordinates play a great role in the deduction of theory,especially the latter one(a flow is often denoted by φtor φ(t,x0) in other literature,but φ has been used as the azimuthal angle in this paper).Denotations used are listed in table 1.The symbolD serves as a differentiation operator w.r.t.the initial conditionx0,as distinguished from those w.r.t.time-like variablest,φsor φe.

Naturally,the Poincaré map P(x0,φ)withx0=(x0R,x0Z)is defined by the standardR-Zsemi-infinite planes P(x0,φ)are used frequently in this paper,different ter-∑(φ) at φ angles,recording the strike points crossing the planes in one direction.If a trajectory flies around ∑(φ)through the opposite semi-infinite plane ∑(φ+π),then by definition the Poincaré map does not record the strike point on∑(φ+π).Since the flow Xpol(x0,φs,φe) and the map minologies are used to distinguish the continuous-time dynamics from the discrete-time one,e.g.equilibrium point,trajectory and cycle are for continuous-time dynamics,while fixed point,orbit and periodic orbit are for discrete-time one.

This paper follows the definitions of stable and unstable manifolds given by Jacob Palis and Welington de Melo [31],(p.73) for a hyperbolic fixed point(p.59) and(p.98) for a hyperbolic cycle(p.95).In both cases the manifolds are defined byω-andα-limit sets,so one can unify the manifold definitions in the continuous and discrete dynamics by considering manifolds of a hyperbolic setS(a definition at(p.160) for the case of a map),since both hyperbolic fixed points and hyperbolic cycles are hyperbolic sets.Note a hyperbolic periodic orbit is also a hyperbolic set,which can be handled by the unified definition.Let(M,f)be a dynamical system,where f is a mapP or a vector field B defined on a metric space or differentiable manifoldM.The stable and unstable manifolds of a hyperbolic invariant setSfor f are defined byω- andα-limit sets,respectively

where the superscripts u and s are short for unstable and stable,respectively.The term hyperbolic ensures the nearby trajectories/orbits on stable(respectively unstable) manifolds approach(respectively get away from)Sat an exponential rate,without which the sets defined above are only qualified to be named stable(respectively unstable) sets [32](p.257),because the stable manifold theorem[31](p.75)requiresSto be hyperbolic.Colloquially,the stable(respectively unstable)manifold is the set of points that will flow into(respectively flowed out of)Sat an exponential rate [32](p.258).Kuznetsov and Meijer simply write f±k(x)→Sask→∞[18](p.4),where f is a map,without explaining what they mean by ‘converging to a setS’,which is suspected to be an alternative denotation ofω- andα-limit sets.

For notational convenience,arguments can be omitted ifsuitable,e.g.are shortforandbyomittingx0,for

3.From field line tracing to invariant manifolds

DXand DXpolimply the change of differential volume and area during FLT,respectively.Suppose a 2D map is written as(x,y) ↦(u,v).The differential area expands,shrinks,or keeps constant after being mapped,as revealed by the following exterior product of differential 1-forms

As Xpol(φs,φe)is a typical 2D map from the section ∑(φs)to ∑(φe),the determinant of DXpol(φs,φe),denoted by∣DXpol(φs,φe)∣,is indeed the same thing as ∂xu∂yv-∂yu∂xv.One could be curious about the geometric meaning of∣DXpol(φs,φe)∣and conjecture that it must be related to the divergence of the field,since it has been well-known [33](p.408) that for∣DX(x0,t)∣

which indicates that,for a divergence-free field,∣DX(x0,t)∣is always zero.A similar formula for∣DXpol(φs,φe)∣is deduced(proof in appendix A.1) to reveal the relationship between∣DXpol(φs,φe)∣and the divergence along the corresponding trajectory Xpol(φs,φ),φs≤φ ≤φe,as shown below

which applies to 3D vector fields of classC1,no matter whether they are divergence-free or not.

More importantly,DP±m(x0,φ)with x0on an X-cycleγofmtoroidal turn(s) decides the two X-leg directions of the X-point.DPm(x0,φ)=DXpol(x0,φ,φ+2mπ)ifBφis positive everywhere.It is the two eigenvectors of DPm(x0,φ)that dictate towards which direction the two invariant manifolds of that hyperbolic cycle grow at the beginning.However,DP±m(x0,φ)itself is more difficult to solve for than its determinant,which is a constant independent of φ for the cycle.This is because the right-hand side of equation(8)becomes a constant as φe=φs+2mπ,i.e.

Unlike the determinant∣DP±m(x0,φ)∣,the matrix DP±m(x0,φ)varies w.r.t the azimuthal angle φ.The evolution rule of DP±m(x0,φ)w.r.t.φ is revealed in section 3.1.

To calculate DXpol(φs,φe)by integrating equation(3)requires thatBφon the trajectory does not change its sign.Otherwise,RBpol/Bφwould be undefined due to zeroBφ.These trajectories are not useless and could be well-defined in Cartesian coordinates.Suppose a trajectory goes from φsto φe,during whichBφmay change its sign for several times.The zeroBφsingularities cause inconvenience to solving for the DXpol(φs,φe).To get around the zeroBφsingularity issue,one can solve for the correspondingDXfirst and then changeits coordinates back to the cylindrical system.The following DXto DXpolformula(proof in appendix A.2)tells how to do so

where the subscripts start and end mean that the corresponding matrices are evaluated at the starting and ending point of this trajectory,respectively,i.e.(Xpol(φs,φs),φs)and(Xpol(φs,φe),φe).

3.1.The evolution of DP±m along a cycle

For a cycle ofmtoroidal turn(s),the relationship among the DP±m(φ)matrices at neighboring sections is desired,without which the calculation of their eigenvectors would spend unnecessarily enormous computational resources.The most primitive approach is definitely repeating the integration of equation(3) from φsto φs+2mπonce and once again for various φs,i.e.from φ1to φ1+2mπ,from φ2to φ2+2mπ...To avoid this horribly primitive approach,the following DP±mevolution formula is deduced(proof in appendix A.3)to reveal how DP±m(φ)varies along the cycle

where the square bracket denotes the commutator,i.e.[A,B]=AB-BA.In the dummy X-cycle demonstration figures 2(a)and(b),section 4.2,arrows are drawn to indicate the directions of eigenvectors.

The DP±mevolution formula can be applied to cycles in autonomousn-dimensional flows(n≥2 and finite).For other dimensions thann=3,the denotation∣DX(x0,T)∣is preferred than∣DPm(φ)∣,whereTis the period of the cycle,because the former one does not rely on the choice of Poincaré section.Then-dimensional version of equation(11) in Cartesian coordinates is shown below

Furthermore,it is desirable to deduce how an eigenvector of DP±m(φ)evolves along an X-cycle,so that one can get rid of the arbitrariness of the computed eigenvector direction,which depends on the specific eigen-decomposition numeric algorithm.If the eigenvector rotates a lot during evolution,the employed numerical method might give a reversed direction without consistency,i.e.the computed eigenvector may jump to the opposite side suddenly.The followingDP±meigenvector evolution formula(proof in appendix A.4) extracts the underlying rule governing the rotation of DPm(φ)eigenvectors along the cycle.Let the eigenvectors of DP±m(φ)be denoted byvi=[cosθi(φ),sinθi(φ)]T,i∈ {1,2}.The derivative of Θ(φ):=diag(θ1,θ2) w.r.t.φ satisfies

where V:=[v1,v2] and Λ:=diag(λ1,λ2).We discovered in numeric implementation that the formula above(13),though accurate,but encounters some numeric issue while handling the X-cycles in island chains,because the two eigenvectors are so close to each other that some matrices in this formula might become pretty singular,i.e.have big conditional number.A much more robust way is to directly use DPm(φ)evolution formula(11) to evolve DPm(φ)and later comb the directions of eigenvectors.

Traditionally,fixed points of 2D maps are classified into hyperbolic,elliptic,and parabolic types based on their Jacobian eigenvalues.For the cycles of 3D flows,the authors want to imitate this naming convention.It is worth emphasizing that the eigenvalues of DP±m(φ)keep constant during evolution.4Hence,it is safe to classify a cycleγofmtoroidal turn(s) by itsDPmeigenvalues.Theλ-invariance ensures the safety of such classification,because one does not need to worry about that the DPm(φ)eigenvalues at different φ are different.

If both eigenvalues ofDPmare not on the unit circleS of C,the cycle is said to be hyperbolic.5If only one eigenvalue on the unit circle,the cycle is called partially hyperbolic(but not fully hyperbolic).If both eigenvalues are onS but neither equal 1 nor-1,the cycle is defined to be elliptic.If the two eigenvalues are identical to 1 or-1,the cycle is defined to be parabolic.

Furthermore,a saddle cycle is defined to be one with|λ1|＜1,|λ2|＞1.Those saddle cycles with both eigenvalues negative(respectively positive) are called Möbiusian(respectively non-Möbiusian).Note that the Möbiusian cycle defined here is different from the classical Möbiusian strip.The cycles with bothλinside(respectively outside) the unit

4 This is a well-known fact in the ODE community,because it is easy to verify that DP(φ2)and DP(φ1)are similar by checkingThe commutator form of the right-hand side of the evolution formulas(11)and(12)also ensures theλ-invariance.Let xibe a right eigenvector ofDP±mandyiTthe corresponding left eigenvector

Given a univariate matrix function A(φ),the derivative of its eigenvalue w.r.t.the single parameter φ satisfies[34].Now substitute A by DP±mas shown below.It immediately lets us know bothλi(φ)of DP±m(φ)do not change with φ

5 This definition is equivalent to the conventional one in[31](p.95),whose Poincaré section is chosen to be transversal to the local vector field.circle S of C are defined to be sinking(respectively sourcing)cycles

Magnetic fields are typical divergence-free fields,in which the so-called X-cycles,O-cycles,and the cycles on rational flux surfaces can now be formally defined as hyperbolic(meanwhile saddle),elliptic,and parabolic,respectively.

3.2.Invariant manifold growth formula in cylindrical coordinates

Letγbe a hyperbolic cycle with real eigenvalues ofDPm.Since the invariant manifold ofγmay grow endlessly,one of the two parameters of the manifold is naturally chosen to be the arc lengthsof the curves intersected by the 2D manifold Wu/s(B,γ)andR-Zcross-sections.For the other coordinate,the azimuthal angle φ is chosen.Define thats=0 on the cycle andsincreases towards the positive infinity as the manifold grows away from the cycle.The diagram(figure A1) in appendix A.5 could be helpful for readers to understand the geometry,which illustrates the relationship among the differentials used.The diagram is put in appendix because those readers who follow the proof there would need it more.

To be accurate,this paper defines a stable/unstable(manifold) branch to be a connected component of the manifold minus its invariant set,i.e.a connected component of Wu/s(f,S)S.For example,a saddle fixed point of a 2D map has 2 eigenvectors and 4 invariant branches.

An invariant branch ofγis parameterized to be Xu/s(s,To deduce the governing equation of Xu/s(s,φ),one simply needs to analyse the differential relationship appearing in FLT,which is concluded in the following invariant manifold growth formula(proof in appendix A.5,requiring no more than knowledge of multivariable calculus)

For Möbiusian saddle cycles,the invariant manifolds can be grown similarly with some subtle difference.A non-Möbiusian saddle cycle has two invariant branches for each stable and unstable manifold.But for a Möbiusian saddle cycle,the ‘two’ branches of a(un)stable manifold are considered as a whole(since they are connected,they are indeed one branch by definition).To parameterize such a branch,double the period of Xu/s(s,φ)in φ from 2mπto 4mπ.Xu/s(s,φ) is opposite Xu/s(s,φ+2mπ) across the cycleγ.Then the growth formula works again.

The growth formula would not grow a rational6flux surface from aparabolic cycle on that surface,since any field line does not cover that surface.To grow this surface,the DP±mevolution formula is sufficient.One simply needs to move the cycle in the directions of the DPmeigenvectors step by step.The role of DP±mevolution formula is to accelerate the computation of DPm(φ) at all sections.For an irrational flux surface,one can choose a non-invariant ‘cycle’ which does not obey the FLT ODE system(1) and then employ the growth formula.For example,in an axisymmetric field,pick a‘cycle’ whoseR,Zcoordinates are constants.The growth formula then degenerates into

therefore,∂Xu/s/∂sis parallel to Bpoland of unit length.

If what is known is limited to one section ∑(φ)(so φ is omitted in this paragraph),then the 2D invariant manifold growth formula degrades to a delay ODE describing 1D 6 In KAM theory,if there exists a diffeomorphismφ:Td→Td(Tdis the standardd-torus) such that the resulting motion on Tdis uniform linear but not static,i.e.dφ(x)dt=ω∈Rd{0}is constant,thenω∈Rdis called a frequency vector(a.k.a.rotation vector) of Td.A frequency vector ω is said to be rationally dependent or commensurable if there exists a vectork∈Zd{0}such that k·ω=0.Specifically whend=2,this paper defnies T2to be a rational(respectively irrational) flux surface if the corresponding ω is commensurable(respectively incommensurable).The frequency vector ω is unique up to a transform of multiplying a square integer matrix A with det A =±1(a.k.a.unimodular matrix) [35,36],i.e.any two frequency vectors ω1and ω2can be transformed to each other by such a matrix ω2=Aω1.Note that the transform of A does not change the commensurability of ω.

Figure 1.(a)and(b) show thesame Möbiusian saddle cycle,of whichthefield is constructedby equation(26) with parameters:(R0,Z0) =(1.0,0.0),Bφ0=2.5,θu(φ)=φ/2+π/2,θ Wu,blue forWs).(a)and(b)drawthemanifoldson φ∈[0,2π]and[0,4π]fora halfand full poloidal turn,respectively.A trajectory on thes(φ)=φ/2,λu/s=-e±1/3.The sproutsof two invariant branchesare plotted(red for unstable branch is drawn for three toroidal turns,i.e.φ∈ [0,6π].

invariant manifolds for a 2D map.Letbe a hyperbolic periodic orbit underP.Parameterize an 1D invariant branch ofby its arc lengthsaswhose inverse is denoted bys(X).Then one can acquire the following equations to grow the manifold by simple analysis along the branch:

where the ellipsis dots…in the denominators,which serve to normalize,denote the same thing as the numerators.Both equations above also hold for an invariant circleC.The only thing that needs to be modified is that the circle should be parameterized as a functionX(s):R →C⊂ R2of period the circumference of the circle,whose inverses(X) :C→ R is now a multivalued function.

4.Demonstration of cycles and invariant manifolds

Having developed the systematic theory to characterize the invariant manifolds in 3D autonomous flows,the formulas have been implemented to present readers with a vivid picture.Two analytic and one real-world examples are presented in this section.As the simplest case,the first analytic model is a saddle cycle as shown in figure 1,which can be either non-Möbiusian or Möbiusian.Next is the more complicated dummy X-cycle model as shown in figure 2,which is acquired by twisting the cycle of the first model,i.e.let theR,Zcoordinates of the cycle rely on φ,instead of being constants.In these two analytic examples,we exhibit the technique to construct a field by the expected trajectories.At last,a timeslice of the magnetic field on EAST is taken as a realworld example as shown in figures 3 and 5,with RMP as the non-axisymmetric perturbation.

4.1.Non-Möbiusian/Möbiusian saddle cycles

In this section,a saddle cycle model is constructed as an analytic example.LetBφ:=R0Bφ0/Rto simulate a tokamak,whereBφ0denotes the toroidal field magnitude at the axisR0.SupposeBφis positive.The trajectories on the invariant manifolds of a Möbiusian cycle are expected to be like

whereλu,λs(independent of φ)denote the two eigenvalues of DPm,θu(φ),θs(φ)denote the corresponding two eigenvectors.If bothθuandθssatisfyθ(φ+2π)=θ(φ)+(2k+1)π,k∈Z,then the cycle is Möbiusian; if they satisfyθ(φ+2π)=θ(φ)+2kπ,k∈Z,then the cycle is non-Möbiusian.

Let ΔXpol(φ):=Xpol(φ)-[R0,Z0]T.For the unstable trajectories,ΔXpol(φ)is

It is similar for stable trajectories,withλu,θu(φ) replaced byλs,θs(φ).Recall the FLT equation(1) in cylindrical coordinates isExpandRBpol/Bφaround the cycle

Figure 2.(a),(b) and(c) show the same dummy X-cycle,of which the field is constructed by equation(32) with parameters:(Rax,Zax) =(1.0,0.0),Bφ,ax=2.5,ι=n/m=1/3,(Rell,Zell) =(0.3,0.5),θu/s(φ)=ιφ+θ0=φ/3+π/2±π/9,λu/s=e±1/5.(a) shows it from the top view,(b)and(c)show it from the other view.(a)and(b)draw arrows for the two eigenvectors ofDP3(φ) and their opposite(blue for λ＜1,red for λ＞1),which is acquired by DP±m evolution formula and shall be consistent with θu/s as designed.The sprouts of four invariant branches are plotted(orange forWu,blue forWs).In(a) and(b),the manifolds are not shown on φ ∈ [6π-2 3 π ,6π),in order not to shelter the eigenvector arrows.A transparent torus with the corresponding elliptic section is drawn for reference.

where the subscript c is short for cycle.The FLT equation turns out to beTo construct a field such that the nearby trajectories are repelled(respectively attracted) atθu(respectivelyθs) as expected in equation(19),it is required that

Eigen decomposition is employed to make it possible to let the first orders of the equations above equal atθuandθs,respectively.As the cost of such decomposition,θu′ andθs′have to be equal,denoted byθ′ afterwards.

For the left-hand side of equation(22)

Bφhas been defined to beR0Bφ0/Rto simulate a tokamak,so ∂RBφ=-Bφ/R.Therefore,the equation above is simplified to

Figure 3.(a)3D visualization of the invariant manifolds of the lower X-cycle γ of EAST shot#103950 at 3500 ms(EFIT+vacuum RMP).The first wall is drawn as a transparent grey surface,with the top removed in order not to shelter the manifolds.(b)Enlarged view of(a)at φ=0 near the lower X-point.

The trajectory equation(19)have been preset by knownλu,λs,θu(φ),θs(φ),which means the right-hand side of equation(22)is what we can control.Based on that,the lefthand side of equation(22)can be calculated,i.e.the field we want to construct,after which the linearizedBR,BZfield is acquired(noteBR,BZat the axis have been preset to zero)

The construction is finished.An example of Möbiusian saddle cycle is shown in figure 1.

The non-Möbiusian case is not shown,because it is easy enough to imagine.Some readers may wonder the higher order termswhich are determined byin the left-hand side of equation(21).

4.2.Dummy X-cycle

In this subsection,R0,Z0in the last model are replaced(see the trajectory equation(19)) withRc(φ),Zc(φ),two functions dependent on φ,respectively.Here,an example expression ofRc(φ),Zc(φ) is given

where the subscript c is short for cycle,ell for elliptic,and ax for axis.Similar to the first model,setBφ(R,Z,φ)=Bφ(R)=RaxBφ,ax/Rto simulate a tokamak.

The zeroth order components of field expansion are denoted byBRc,BZc,Bφc,to highlight that they are evaluated on the cycle,e.g.Bφc=Bφ(Rc(φ),Zc(φ),φ).According to the spiral cycle equation defined above,the following equalities hold

The first order of expansion,∂Bpol/∂(R,Z),is calculated by equation(25)

Expand the poloidal field around the cycle up to first order,

Figure 4.Illustration of the numeric algorithm to grow an invariant branch from an X-point for a map.

The construction is finished.A dummy non-Möbiusian X-cycle withq=m/n=3/1 is shown in figure 2.

4.3.A real-world example

The equilibrium field of EAST shot # 103950 at 3500 ms given by EFIT is taken as background,superimposed with a non-axisymmetric field induced by the RMP coils running inn=1 mode.The plasma response is not considered here for simplicity.Bφof this shot is negative everywhere,and BpolatR-Zcross-sections is clockwise.

On locating the periodic points of the Poincaré map,the simplest discrete Newton methodxj+1=xj-h[DG(xj)]-1G(xj)is employed [37],where G(x):=F(x)-I and I is the identity map.To locatem-periodic orbits of the Poincaré map P(φ)at the section φ,our map F is chosen to be themth iterate of P(φ),that is Pm(φ).

After locating the cycle,one needs to know the DPm(φ)of this cycle at every section,which is the job ofDP±mevolution formula.This formula is a traditional matrix ODE system.The Python function scipy.integrate.solve_ivp and the Julia package DifferentialEquations.jl have prepared a lot of numeric algorithms for such ODEs.Next is to eigen decompose DPm(φ),which can be done by,for example,the Python function scipy.linalg.eig.The two eigenvectors of DPm(φ)and their opposite are the directions towards which the invariant manifolds grow at the beginning.

Recall the invariant manifold growth formula

only requires two variables on the right-hand side,RBpol/Bφand ∂Xu/s/∂φ.In the numeric implementation,RBpol/Bφis linearly interpolated on a regular grid of shape[nR,nZ,nφ].For ∂Xu/s/∂φ,different people have different ways to handle it numerically.In the following two subsections,two approaches to grow manifolds are exhibited.

4.3.1.Naive field line tracing.The simpler scheme is to distribute a line of Poincaré seed points along the eigenvector of a periodic point.To compute the arc lengthsof a branch of Wu/s(Pm,x0)requires the FLT Poincaré orbits used to construct the manifold be ordered,which is achieved with the assistance of the DPm(φ)eigenvalues in this paper.

Suppose x0is a saddle fixed point of the 2D Poincaré mapP at anR-Zsection.Denote the unstable eigenvalue and eigenvector of DP(x0)byλuand vu.If x0is instead anmperiodic saddle point,one simply needs to substitute DPm(x0)for DP(x0).Seed a line of points(x1,...,xN)along vu,equally spaced,i.e.xi+1-xiis a constant for 0≤i≤N-1.Ifλu≤N,P(x1)probably falls behind xN,i.e.thesof P(x1) is smaller than that of xN.This makes it difficult to computes,because the order ofsis not certain.Let X be a sequence defined by

It is expected that thesof P(x1)should be greater than that of xN,thesof P2(x1) should be greater than that of P(xN),and so on,i.e.thesof Pk+1(x1)should be greater than that of Pk(xN),as shown in figure 4.In fact,as long as thesof P(x1) is greater than that of xN,the conditions fork≥1 are naturally satisfied.Now that P(x)≈x0+λu(x-x0)in the neighborhood of x0if x is in the direction of vu,one simply needs to put xNcloser to x0than P(x1),so thats(Pk(xN))＜s(Pk+1(x1)).By virtue of this fact,the orbits are untangled with ease and one gets rid of tentative manifold growth methods[11-15],which need to decrease growth step when the local manifold curvature is large.In other words,it is ensured that the sequence

is a strictly increasing sequence,which guarantees that it is safe to computesby simply accumulating the lengths of segments.Apart from this advantage,this technique to grow manifolds applies to hyperbolic fixed points ofn-dimensional maps,n∈N+.

The invariant manifolds in figures 3 and 5 are grown by this naive FLT technique,of which the computed arc lengthssare expressed by the varying color to let it be more easy-tounderstand.One can immediately observe that the confinement of this equilibrium relies mostly on the invariant manifolds of the lower X-cycleγlow,although it also has one X-cycle at top.It is also known as the disconnected doublenull configuration.

Figure 5.(a) Poincaré plot at φ=0 of EAST shot #103950 at 3500 ms(EFIT + vacuum RMP).Some invariant manifolds are grown and plotted.(b)Enlarged view of(a)near the lower X-point.Dense scatter points with color are presented to show how the regions are connected by field lines.(c) Enlarged view of(b) near x1.The blue arrows are drawn according to equation(35).

The blue arrows in figure 5(c)are drawn by the invariant manifold growth formula,which takes ∂Xu/s/∂φ and gives∂Xu/s/∂s.Evidently,∂Xu/s/∂sis the growth direction of a manifold.The first order central scheme is employed to calculate ∂Xu/s/∂s(s,φ)by Xu/s(s,φ)at the two neighboringR-Zsections φ±∊

4.3.2.Discretizing the invariant manifold growth partial differential equation(PDE)to an ODE system.The other numeric way is to transform the invariant manifold growth formula,a PDE including ∂sand ∂φ,to a system of ODEs withsas the evolution parameter.Transect the invariant manifold byN R-Zcross-sections atto discretize it,whereis an arithmetic sequence with a common difference Δφ=φi+1-φiranging from 0 to 2mπ-Δφ.TheRandZcoordinates of the manifold at each section contribute two variables of the system,totally 2Nvariables contributed byNsections.Thereafter,become univariate functions dependent ons.The manifold growth formula is thereby reduced to a 2N-dimensional ODE system

where ΔXu/s(s,φi)/Δφ denotes a numeric alternative of ∂Xu/s(s,φ)/∂φ.For example,it can be defined as the first-or second-order central difference schemes

This discretizing method works fine for the invariant manifolds of the outmost saddle cycle(s),but not so for theq=m/n=3/1 island chain,in which case the four numerically grown invariant branches around an island are almost identical and can not be distinguished as if there were no island there.The primary reason is suspected to be that the two eigenvectors are so close to each other that the grid granularity is not fine enough to distinguish the branch growth directions by finite difference.Although this scheme suffers such a numeric instability,the authors still think it is worth introducing,because this scheme directly utilizes the invariant manifold growth formula and can be useful for those cases that the two eigenvectors of DPmare not so close.

4.3.3.Denotations and notions explained with the aid of figures.A periodic orbit for a map is best seen as a whole to reflect the intrinsic homoclinic/heteroclinic structure.Then,one can use Wu(P,{x1,x2,x3})to denote all the unstable branches of the X-cycle of theq=m/n=3/1 island chain in figure 5.This X-cycle has three strike points{x1,x2,x3}through φ=0 section,each of which has two stable and two unstable branches.Totally there are 6 branches of Ws(P,{x1,x2,x3})and 6 branches of Wu(P,{x1,x2,x3}).One can also specify a manifold in a more fine-grained way by replacingP withPm,{x1,x2,x3}with xi,that is Wu(P3,xi)and Ws(P3,xi),which represent the two unstable and two stable branches belonging to the specific point xi,respectively.Obviously

The 2D manifold Wu/s(B,γ)consists of all the corresponding 1D manifolds Wu/s(Pm(φ),x(φ))for the Poincaré mapsPm(φ) at all sections φ,i.e.

where x(φ) denotes the(R,Z) coordinates of the cycleγat φ angle,and P(φ):denotes the Poincaré map at φ.where x(φ) is a 6π-periodic function representing the(R,Z) coordinates of this X-cycleγ.P(x0)=x1,P(x1)=x2,P(x2)=x3.Then,x(0)=x1,x(-2π)=x2,x(-4π)=x3(Bφis negative in this shot).Viewing the 3D figure 3 and 2D figure 5 together can help understand the relationship between 2D manifolds Wu/s(B,γ)and 1D manifolds Wu/s(Pm(φ),x(φ)).

In figure 5(b),some regions enclosed by the invariant manifolds ofγloware filled by colored scatter points.Points are marked with distinctive colors,and then mapped byP-1.How these regions are connected by field lines is reflected through the color pattern of scatter points.Let xlowbe the strike point ofγlowcrossing the φ=0 section.All the points of transversal intersection of the two manifolds Wu(P,xlow)and Ws(P,xlow)(the red and blue curves,respectively) are homoclinic to xlow.

Although the fluxes in the colored regions filled by scatter points are the same,e.g.the ①and ②regions in figure 5(b),this flux value probably differs from that of the uncolored regions,e.g.③and ④.One should always be careful of this fact.

5.Discussion and conclusion

5.1.Comparisons with existing works

This subsection compares various approaches developed to study invariant manifolds,albeit obvious.The comparisons of ourDPmevolution and invariant manifold growth formulas with others’ works are presented in this subsection subsequently.

Most of existing research has been satisfied with the Floquet’s normal form.Floquet theory is so successful that people cease further exploration.Floquet theorem governs how DXpol(φs,φe)varies with φe.However,it remains unclear how DXpol(φs,φs+2mπ)changes with φs,which is essential to lessen the computational resources needed to solve for the initial growth directions of stable and unstable manifolds.The most similar work toDPmevolution formula is given by Tsutumi [38].Tsutumi considered the following linear system:

where x=x(φ,t)is a complexn-column vector and A(φ,t)is a complexn×nmatrix functionT-periodic in φ.Theorem 1.in [38] is repeated as below:

There exists a monodromy matrix of(1.1)which does not depend ont7if and only if there exists a matrix function Γ(φ,t) which is defined on ∞＜φ,t＜∞,T-periodic in φ,and satisfies

7In[38],‘there exists a monodromy matrix of(1.1)which does not depend ont′ is equivalent to that ‘the internal structure of every monodromy matrix of(1.1) does not depend ont′.By internal structure,Tsutumi means the characteristic multipliers of a matrix and their algebraic and geometric multiplicities.

Table 2.Manifold expression comparison.

Tsutsumi’s equation(1.2) above is more complicated than ourDP±mevolution formula(11)because A(φ,t)relies on both φ andt.If ∂A/∂tvanishes,one can easily observe that Γ is governed by the same equation asDP±mevolution formula.Tsutsumi did not explain in [38] what Γ can be and how to construct it.His attention was paid to the condition of A(φ,t)such that the monodromy matrix does not depend ont.This condition is revealed in his theorem by the existence of the matrix function Γ which satisfies equation(1.2).

The works similar to our invariant manifold growth formula are collated into table 2,in which the work of SS Abdullaev is discussed in the next paragraph and appendix B in more detail.As shown in table 2,the classical invariance equation(1.7) in [10] forn-dimensional maps might be too general for fusion scientists to be useful.TE Evans,JP England,and JM Ottinoet alfocused on numerical or experimental methods rather than analysis.

Abdullaev [30] has made some contributions to establishing the formula of stable and unstable manifolds.Here we point out the following facts worth noting about his work:(a)his theory relies on the assumption that the perturbation to an axisymmetric magnetic field is small so that the FLT system can be transformed to a perturbed Hamiltonian form;(b) the Poincaré integral is employed to acquire a first order approximation to Poincaré map.By contrast,our Poincaré map is exact;(c)the final formulaF(s,u)(φ,x,y)=0 is implicit instead of explicit;(d) the(x,y) coordinates appearing in the formula are not the standard(R,Z) cylindrical coordinates.Thex- andy-axes are even probably not perpendicular.A more detailed comparison equipped with equations is put in appendix B.

5.2.Conclusion

Although the magnetic fields in tokamaks are mostly considered axisymmetric,almost all kinds of auxiliary heating schemes,except the ohmic heating of the central solenoid,are strongly localized and non-axisymmetric.The topology of magnetic field plays a dominant role in the behaviour of the confined plasma and the scrape-off layer.Motivated by the curiosity about the intrinsic characteristics of general 3D vector fields(not necessarily divergence-free),an analytic theory on the invariant manifolds of cycles is established in this paper,where the short-period cycles are regarded the skeleton of fields.

The stable and/or unstable manifolds of hyperbolic cycles grow from the eigenvectors of DP±m(φ).ByDP±mevolution formula(11),one gets rid of repetitive 2mπ-integration of equation(3) for DP±m(φ) at every angle φ.The primitive FLT ODE system(1) is extended to the invariant manifold growth formula in cylindrical coordinates(16) by analyzing the relevant differentials.

It is proposed to use the notion of invariant manifolds of outmost saddle cycle(s)to characterize the magnetic topology atthe plasma edge when the field is strongly non-axisymmetric.If a tokamak operates in the single-null(respectively double-null,or somehow more strange)mode,there is one(respectively two,or more) outmost saddle cycle(s).The transversely intersecting manifolds are suspected of causing the spiral ribbon-like pattern of heat deposition on the divertor found in tokamak experiments,which needs further verification.In the scrape-off layer,how to disperse the particle and heat fluxes before they land on the divertor is also an interesting problem,worthy of more investigation.With the drift effects taken into account in the future,the heat load pattern observed by diagnostics like infrared thermography is supposed to be more consistent with the divertor regions covered by the invariant manifolds of outmost saddle cycles.For both tokamak and stellarator communities,the transport issue at the plasma boundary is essential to control the heat load below the material limit.

Acknowledgments

This work was supported by National Magnetic Confined Fusion Energy R&D Program of China(No.2022YFE03030001),National Natural Science Foundation of China(Nos.12275310 and 12175277),the Science Foundation of Institute of Plasma Physics,Chinese Academy of Sciences(No.DSJJ-2021-01) and the Collaborative Innovation Program of Hefei Science Center,CAS(No.2021HSCCIP019).

Appendix A.Proofs

A.1.The geometric meaning of∣DXpol（φs，φe）∣

Proof.

To further simplify the expression above,prepare the following differentials

Reorganize the terms at the right-hand side of equation(A4)in a much more compact way

(Here ln is the complex logarithm instead of the real one.So it can handle negative numbers).

A.2.DX toDPformula

Csand Ceare the matrixevaluated at the starting and ending points,respectively.

Proof.Consider the differential relationship in cylindrical coordinates

Suppose that the solutionX(x0,t)crosses theR-Zcrosssectionφeat the timeT.The relevant differentials are related by the equation dX(x0,T)=DX(x0,T)·dx0as detailed below

wherex0andX(x0,T)denote the starting and ending points,respectively.A similar differential analysis is done forXpol(·,φs,φe)as below

The equation above always holds for any dx0R,dx0Z,and dx0φ,hence the corresponding coefficients shall equal

A.3.DP±m evolution formula

Proof.Integrating equation(3) w.r.t.φefromφstoφs+Δφ

Differentiating both sides of equation(A18) w.r.t.φs

Though it is known how to calculateas shown in equation(3),little is known aboutNotice that DXpol(φs,φe)is the inverse matrix of DXpol(φe,φs).The following equation(A23) is useful to solve for(K-1)′by K(x)and its derivative K′(x),where K(x)is a univariate matrix function

Borrow the equation(A23) to solve foras shown below

Next,calculate the total derivative of DXpol(φs,φs+Δφ)w.r.t.φs.Letφe=φs+Δφ

For trajectories ofmtoroidal turn(s),A(φs)and A(φs±2mπ)are identical since A is a periodic function on the cycle

LetΔφbe±2m π,then DXpol(φs,φs+Δφ)can be substituted by DP±m(φs).Equation(A25) is simplified to

One might suspect whether equation(11) works for DP-m,the inverse of DPm.Consider DP-m=(DPm)-1.By equation(A23)

which indicates that the formula(11) applies for bothPmand its inverseP-m.

A.4.DP±m eigenvector evolution formula

Proof.Firstly,the eigenvectors are parameterized byθas shown below

which is safe because,according to theλ-invariance property,the eigenvectors would not become complex on saddle cycles.

Concatenate the two eigenvectors into a matrixV,then

Differentiating equation(A29) w.r.t.φ

V′ can be simplified by

Θ and Λ are diagonal and hence commute,therefore equation(A30) becomes

For cycles,(DPm)′=[A,DPm]implies thatλ1′=0,λ′2=0 as shown by the equation(15),then Λ′=0and equation(A33) is simplified to be

A.5.Invariant manifold growth formula

Proof.The relationship among the differentials ds,dφ,dR,and dZis shown in figure A1.To solve for dsdφ,the differentialdsis given as below

Dividing both sides by dφ2

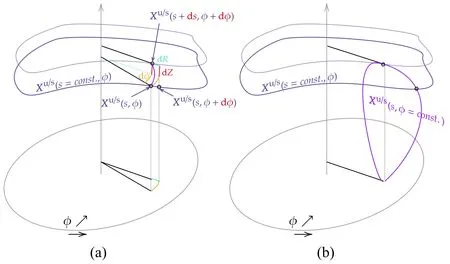
Figure A1.Geometric diagram to show the relationship among the differentials ds,dφ,dR,and dZ.It is supposed that there exists a hyperbolic cycle at bottom,from which an invariant manifold grows.(a)The differential involved in FLT,(b)Two iso-s curves and one iso-φ curve of the manifold.

TheZcomponentis similar.

Appendix B.Comparison with Abdullaev’s work

Abdullaev firstly transforms the standard cylindrical coordinates(R,Z) to the canonically conjugated variables(z,pz):

whereB0is the toroidal magnetic field strength at the major radiusR0,andA=(AR=0,AZ,Aφ)denotes the vector potential of magnetic field.The normalized poloidal fluxψpserves as the Hamiltonian.However,this transform is not always viable when the magnetic field is non-axisymmetric(the definition ofψprequires a closed flux surface diffeomorphic to T2),which limits the application of Abdullaev’s method to those near-integrable systems.After that,the FLT equations are presented in the following Hamiltonian form:

A non-axisymmetric magnetic perturbation changes the original axisymmetic poloidal fluxto:

where ∊is a dimensionless perturbation parameter dictating the relative strength of perturbation,anddenotes the perturbation magnetic flux.Such a denotation implies an additional numeric step to transform the perturbation field Bpert(R,Z,φ) toBy comparison,B=B0(R,Z)+Bpert(R,Z,φ) is taken as a whole in our theory,without need to distinguish the perturbation field from the field to be perturbed.

The Poincaré map in [30] is defined to be a full poloidal turn map,with the Poincaré section ∑sconsisting of two segments of theξ- andη-axes.(ξ,η) is a rectangular coordinate system centered at the X-point(see figure 1 in [30]).Note thatψpvaries along theξ-axis.Under the perturbation,the Poincaré map(φk,ψk) ↦(φk+1,ψk+1) has the following classical general form:

where the upper and lower signs correspond to the φincreasing and φ-decreasing Poincaré maps,respectively.P(φ;ψ)is an integral ofalong the unperturbed trajectory,a.k.a.the Poincaré integralBe careful that the equality of equation(8)only holds when ∊is infinitesimal,otherwise it is suggested to use≈instead of=in equation(8)or add a remainder to for correctness.Equation(8)is the basis for many other equations in [30],which probably also need to change to≈when applied to a realistic ∊.

Letψk+1=0 at φk+1→±∞in equation(8),then Abdullaev immediately obtains the following implicit form of the subset of these two manifolds on ∑s:

where the upper and lower signs correspond to the stable and unstable manifolds,respectively.

For the points of these two manifolds not on ∑s,they are mapped to ∑salong the field lines by equation(36) in [30].Under the assumption that the magnetic perturbation at the X-point is small and can be neglected,ax,aycoefficients in equation(36) are omitted to obtain the following simplified implicit manifold expression:

Note that(x,y) in [30] are not the standard cylindrical coordinates(R,Z),but defined by

whereα,βcome from the second order term of the expansion ofhin the(ξ,η,φ) coordinate system

Remind thatx-andy-axes are not necessarily perpendicular.The slope ofx-axis in(η,ξ) plane isβ/α(y=onx-axis),while that ofy-axis is-β/ony-axis).The product of their slopes equals-β2/α2,which does not necessarily equal-1.

ORCID iDs