基于减沙效益和经济效益的流域退耕还林方案优化
喻 丹,董晓华※,彭 涛,刘 冀,刘 超,刘 芳
(1.三峡大学水利与环境学院,宜昌 443000;2.三峡库区生态环境教育部工程研究中心,宜昌 443000;3.宜昌市夷陵区水资源利用服务中心,宜昌 443000;4.宜昌市水文局,宜昌 443000)
0 引言
土壤是人类赖以生存和发展的基础自然资源,由于特殊的地理和历史条件,中国水土流失量大且面积广,是突出的生态环境问题之一。在众多导致水土流失的因素之中,耕地又被认为是水土流失的主要策源地[1]。为了遏制水土流失、改善生态环境,中国于1999 年启动实施了退耕还林工程,在长江、黄河和淮河等流域的长期实践看,其控制水土流失的效果十分显著。2014 年国家林业局启动了新一轮的退耕还林工程,旨在进一步推进中国的生态文明建设。
退耕还林是一项涉及社会、经济和生态多个方面的复杂系统性工程,工程的实施既要重视生态效益,又要兼顾社会经济效益,因此客观评价退耕还林工程的成本有效性已成为衡量其是否成功的关键指标。目前已有学者围绕退耕还林实施后的生态效益评估[2-5]、经济效益评估[6]以及综合效益评估[7]进行了大量的研究。然而由于受到气候、下垫面特征以及区域经济产业结构的影响,退耕还林工程的各项效益存在着一定的空间差异[8-10]。
仅根据退耕还林工程实施后所进行的“事后评价”难以直接给与管理决策者用于规划退耕还林工程空间布置所需要的“事先评价”的信息。如何预先制定最具成本-效益的退耕还林方案,以平衡生态和经济之间的矛盾,已成为保证退耕还林工程可持续发展的关键。多数研究采用基于情景分析(scenario-based)的方法对退耕还林工程进行优化配置,即依据一定的准则条件形成几个退耕还林空间配置方案,再根据评价结果进行方案比选、择优。黄康等[11-13]均根据不同的坡度设置了多个退耕还林情景,李越强等[14-15]则通过设置极端的情景,即假设全流域的耕地全都进行退耕还林。于航等[16]以陡坡和河岸带的耕地为目标区域,设置了4 种不同的退耕还林情景。显然这种基于情景分析的方法对于情景的假设是有限的,无法全局覆盖退耕还林的所有情景,从而丢失潜在的更优的配置方案。因此,需要探索基于全局搜索寻优的方法实现退耕还林空间配置方案的优化。
淮河流域是中国中东部地区重要的生态安全屏障,水土流失一直都是流域生态保护所面对的主要问题。2021 年度全国水土流失动态监测成果显示淮河流域的水土流失表现为水力侵蚀为主,且主要分布在沂沭泗河、沙颍河以及淮河干流的上游区域[17]。在淮河典型流域开展退耕还林的空间配置研究对淮河流域水土流失综合治理以及生态环境保护具有重要的意义。本文选择淮河上游的息县流域为研究区,先运用生态水文模型模拟和GIS 空间叠置方法分别构造退耕还林的生态效益目标和经济效益目标,再以子流域为水土流失治理单元构成多目标优化问题,采用具有全局搜索能力的智能算法求解子流域尺度的退耕还林优化方案,为淮河流域水土保持、退耕还林工程的科学规划提供借鉴和指导。
1 研究区概况与数据来源
1.1 研究区概况
淮河流域(东经111°55’~121°25’,北纬30°55’~36°36’)位于中国东部、长江和黄河两大流域之间。淮河干流发源于河南省南阳市桐柏县和湖北省随州市随县交界处的桐柏山太白顶,流经河南、湖北、安徽和江苏,全长1 000 km,流域总面积为27 万km2。本文选取淮河干流上游的息县水文站以上流域作为研究区(下文简称息县流域),研究区概况如图1 所示。
息县流域面积为10 219.67 km2,流域内以山区和丘陵区为主,地势由西南和北部的山区逐渐向东降低。根据中科院资源环境科学数据中心提供的中国多期土地利用遥感监测数据集(CNLUCC)以及沈玲怡等[18]对息县流域2000—2020 年的土地利用变化分析可知,2000 年之后息县流域并未发生明显的土地利用变化,且耕地始终是流域主要的土地利用方式。以淮河干流为分界线,干流以北的耕地种植着玉麦和玉米为主的旱地作物,干流以南的耕地多为水田,主要种植水稻。其次是林地,主要分布在流域河源区域的桐柏山一带。林地垂直分带明显,可分为中山落叶阔叶林,低山常绿落叶阔叶混交林,丘陵常绿针叶林及经济林[19]。然而,人口的增长和社会经济的发展导致了息县流域土地资源的不合理利用,流域内许多地区的自然植被遭到了破坏,加之耕地降低了土壤的抗侵蚀能力,因此引发了水土流失这一生态环境问题[20]。息县流域已被水利部划分为国家级水土流失重点预防区,此外还被纳入第四期和第五期的全国水土保持重点工程建设项目规划[21]。
1.2 数据来源
本研究使用的数据包括:研究区地形数据DEM(digital elevation model),来源于美国太空总署和国防部国家测绘局联合测量的SRTM-DEM 数据(http://srtm.csi.cgiar.org/),其空间分辨率为90 m;土地利用空间分布情况从中国科学院资源环境科学数据中心(https://www.resdc.cn/Default.aspx)提供的中国多时期土地利用遥感监测数据集中提取,空间分辨率为30 m;土壤数据来源于联合国粮农组织和维也纳国际应用系统研究所所构建的世界土壤数据库Harmonized World Soil Database -HWSD(https://www.fao.org/soils-portal/soil-survey/soilmaps-and-databases/harmonized-world-soil-databasev12/en/),空间分辨率为1 km;本研究采用中国GDP(gross domestic product)空间分布公里网格数据来表征研究区的社会经济状况,该数据来源于中国科学院资源环境科学数据中心(https://www.resdc.cn/Default.aspx),空间分辨率为1 km;研究流域内共计42 个雨量站的日降雨数据以及流域出口息县水文站的流量观测数据均由淮河水利委员会提供,时间范围为1995—2010 年;其他气象参数通过美国国家气象预报中心提供的全球气候再分析系统CFSR 计算得到。
2 研究方法
2.1 退耕还林的减沙效益
在降雨的驱动作用下,土壤侵蚀剥离的泥沙伴随着流域水文循环过程而迁移。流域生态水文模型不仅能对流域的水沙过程进行有效模拟,还能定量评价水土保持措施对流域水沙的影响。SWAT(soil and water assessment tool)模型被广泛应用于预测不同土壤类别、土地利用类型以及管理措施下流域的水量、泥沙及水质变化,具有较强的适用性[22]。根据研究区DEM 数据,SWAT 模型将全流域共划分为49 个子流域,如图1 所示。本研究选择的土地利用数据时期为2010 年,土地利用分类依据的是中国土地资源分类系统,为了与SWAT 模型所含的土地利用数据库对应,如图2a 所示将其重分类为耕地、林地、灌木、草地和水域,其中耕地和林地为研究区的主要土地利用类型,分别占全流域的55.41%和22.08%。基于HWSD 土壤提取本研究区的土壤类型空间分布如图2b 所示,土壤类型的划分依据FAO -90 土壤分类系统,其中堆积土和不饱和始成土为研究区的两种主要的土壤类型,所占比例分别为28.66%和21.95%。由于SWAT 模型自带的土壤数据库没有覆盖到本文的研究区,故根据魏怀斌等[23]提出的方法计算土壤参数。根据相关研究[24]推荐的HRU(hydrologic response unit)划分阈值(坡度10%、土地利用0、土壤10%),最终在研究流域划分了528 个HRU。

图2 研究区土地利用空间分布和土壤类型空间分布Fig.2 Land use and soil types throughout the study area
采用本研究收集到的研究区雨量站点的降雨数据和天气发生器的气象参数驱动SWAT 模型,以研究流域出口息县水文站实测的径流和泥沙数据作为参照,以1995年为预热期,1996—2003 年为率定期,2004—2010 年为验证期,采用SWAT-CUP 的SUFI-2 算法分别进行月尺度的径流参数率定以及月尺度的泥沙参数率定,选取统计指标Nash 系数(Ens)、决定系数(R2)和百分比偏差(PBIAS)对SWAT 模型率定期和验证期的模拟精度进行评定。
流域管理措施产生的效果会随着配置地点地形、水文气候、土壤等特征的不同而不同[25]。本研究利用SWAT模型来量化空间不同位置进行退耕还林起到的水土保持效果。将建立SWAT 模型采用的2010 年土地利用为基准,以子流域为退耕还林的基本单元,每次仅选择一个子流域(如子流域i)进行退耕还林操作,再利用率定好的SWAT 模型进行模拟,得到该子流域退耕还林后流域的产沙值Si,依次遍历所有子流域,根据式(1)计算子流域退耕还林的泥沙削减系数Sci。
式中S0为基准期土地利用条件下SWAT 模型模拟的流域产沙值,t;Si为子流域退耕还林后流域的产沙值,t;A耕i为 基准期土地利用条件下第i个子流域中退耕还林的面积,即是基准期该子流域耕地的面积,km2。
2.2 退耕还林的经济效益
土地是区域经济发展的最基本物质载体,土地利用和经济发展有着密不可分的关系,社会经济结构的变化直接决定了土地利用方式的变化。淮河流域作为中国重要的粮食生产基地,其农业产值和人均农业产值均高于全国同期水平,流域内的耕地资源有着极其重大的经济价值。因此可认为在息县流域实施退耕还林会给区域经济造成一定的影响。本研究采用资源环境科学与数据中心提供的中国GDP 公里网格分布数据来表征研究流域的经济发展水平,该数据是在综合分析了人类活动形成的土地利用格局与GDP 的空间互动规律的基础上,建立一二三产业GDP 数量与土地利用类型的空间相关性模型来实现GDP 的空间化,且认为耕地、林地、草地、水体这些土地利用类型只贡献第一产业GDP,第二三产业GDP 值仅与城乡工矿居民地有关[26]。因此本研究针对的是退耕还林后第一产业的GDP 损失。
将2010 年的中国GDP 公里网格分布数据与基准期2010 年的土地利用数据进行空间叠置分析,分别得到基准期土地利用条件下耕地和林地覆盖的GDP 产值空间分布,再结合子流域空间分布可统计第i个子流域内耕地和林地分别对应的第一产业GDP,分别记为G耕i和G林i,并假设在同一个子流域内,单位耕地或者单位林地产生的GDP 是均匀的。那么在基准期土地利用条件下,第i个子流域的第一产业GDP 值G0i可表示为
选择第i个子流域进行退耕还林,退耕面积为A耕i,同时保持其他子流域的土地利用不变。退耕还林后该子流域原有耕地产生的GDP 产值就全部损失了,林地面积在原有的基础上增加了。因此第i个子流域的第一产业GDP 值Gi可表示为
式中A林i为基准期土地利用条件下第i个子流域内林地的面积,km2。
由式(2)和式(3)即可推求退耕还林过程中第i个子流域第一产业GDP 产值的变化,记为△Gi:
为了消除退耕还林面积的影响,定义GDP 损失系数Gci为单位退耕还林面积的GDP 变化,具体表达式为
重复上述操作依次遍历所有的子流域,即可得到空间不同子流域的GDP 损失系数。Gci>0 表示GDP 在基准期的基础上增大,Gci<0 表示GDP 相较于基准期减小。
2.3 基于多目标遗传算法的退耕还林方案优化
以小流域为单元的水土流失综合治理是中国水土保持工作的重要途径,因此设定第i个子流域参与退耕还林面积xi为自变量。结合前述的泥沙削减系数Sci和GDP 损失系数Gci构造研究区退耕还林的多目标优化问题,一方面生态效益目标F1可由退耕还林后流域的泥沙产量来表示,如式(6)所示;另一方面用退耕还林导致的第一产业GDP 损失值来表征经济效益目标F2,如式(7)所示。约束条件表示为每个子流域的退耕面积约束,如式(8)所示。
式中n为退耕还林的子流域个数。
本研究采用多目标遗传算法NSGA-II[27]对式(6)~(8)所描述的优化问题进行求解。NSGA-II 是基于Pareto 最优概念的遗传算法,用以解决多个冲突目标之间的最优化问题,其Pareto 前沿是由多个解构成的最优解集,且各Pareto 最优解之间没有优劣之分。针对本研究的优化问题,一个空间退耕还林方案xi(i=1,2,…,n)就是一个个体,NSGA-II 算法首先在约束条件下以随机的方式生成初始化种群,即是一定数量的空间退耕还林方案;再根据生态效益目标F1和经济效益目标F2对每一个方案进行多目标评价;运用算法的非支配排序、交叉、变异等操作产生新的子代种群;经过迭代进化最后得到最终的退耕还林Pareto 方案集。
优化出的Pareto 前沿上存在一个向理想点方向的“凸起”,为Knee 解。Knee 解是Pareto 前沿上具有极大边际效用的点,若没有制定特定的偏好,则Knee 解被认为是最具成本-效益的点,因此是最有可能被决策者优先选择的点。采用基于距离的方法确定Knee 解:根据Pareto前沿的极端点形成一条直线,计算Pareto 前沿上所有点到该直线的距离,距离最大的点解即为所求[28]。
3 结果与分析
3.1 SWAT 模型模拟结果
根据相关研究[29]确定如表1 所示的对径流和泥沙模拟影响较大的敏感参数参与率定。SWAT 模型参数率定结果如表1 所示,径流和泥沙模拟精度评定结果如表2所示。可以看出径流模拟率定期和验证期的Ens值均在0.90 以上,决定系数R2的值接近于1,且总量误差PBIAS控制在-10%以内,说明月尺度径流模拟的精度较高。相比之下,月尺度的泥沙模拟结果要略差于径流。泥沙模拟率定期和验证期的Ens值均能够保持在0.70 以上,R2值大于0.80,PBIAS的值在10%至20%之间,表现出一定的总量误差,但依据精度指标判定标准来看仍处于可接受的范围。通过SWAT 模型模拟的月径流和月泥沙与实测过程的对比线(图3)可以看出,SWAT 模型能够较好地重现研究流域径流和泥沙随时间的变化过程。综合分析认为本研究建立的SWAT 模型对研究区的月径流和泥沙模拟具有较好的适用性。

表1 SWAT 模型径流参数和泥沙参数率定结果Table 1 Optimal values for runoff and sediment parameters in SWAT model

表2 SWAT 模型精度评定结果Table 2 Accuracy evaluation results of the SWAT model

图3 SWAT 模型模拟的月径流和月泥沙与实测过程的对比Fig.3 Comparison of monthly runoff and sediment simulated by SWAT model with measured processes
3.2 子流域泥沙削减系数
根据现状土地利用条件下的SWAT 模型模拟结果,统计得到基准期流域多年平均泥沙产量为210.7 万t,与邹宏荣等[30]对息县流域产沙模拟的结果较为一致。子流域实施退耕还林操作后,各子流域泥沙削减系数的空间分布如图4 所示,空白部分表示该子流域没有耕地,故不参与退耕还林。根据式(1)可知,计算的Sci数值越大,说明在该子流域实施退耕还林达到的减沙效果越好。由图4 可以看出,Sci在子流域空间上呈现出一定的空间过渡趋势,表现为上游河源区的值较大,中游到下游区域的值逐渐变小。说明对于单位面积的退耕还林操作,上游的河源区域能够取得更加明显的减沙效果。流域水系的河源区一般山高坡陡且降雨量较大,已有研究证明坡度和降雨对土壤侵蚀有着很大的促进作用[31-33],因此该区域属于水土流失敏感区,不适合于发展耕地。Sci数值最小的3 个子流域依次为子流域18(26.70 t/km2)、子流域19(28.49 t/km2)和子流域12(29.22 t/km2),从空间分布上看这3 个子流域集中在流域下游干流以北的区域。
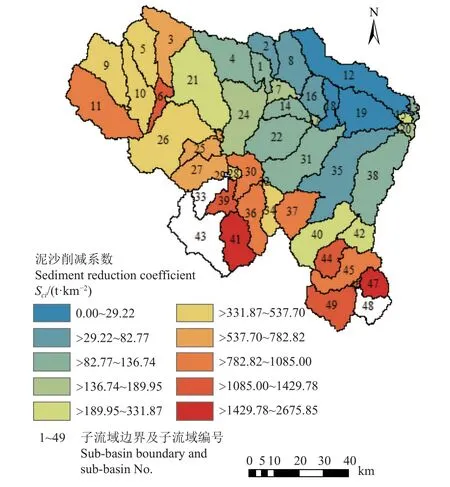
图4 泥沙削减系数Sci 在子流域空间的分布Fig.4 Spatial distribution of sediment reduction coefficient Sci at sub-basin scale
3.3 子流域GDP 损失系数
结合现状土地利用和GDP 网格数据叠置分析得到基准期条件下研究流域总GDP 值为515.61 万元,且各子流域内林地和耕地覆盖的GDP 值如表3 所示,对比可知对大部分子流域来说,耕地比林地产生了更高的GDP,这也与淮河流域农业经济占主导地位这一事实相符。仅有部分子流域,如34、41 和44,其林地产生的GDP 略大于耕地。此外,子流域GDP 损失系数计算结果如表3所示,可以看出实施退耕还林后子流域GDP 的变化有着较大的空间差异,不仅出现了GDP 的降低,同时还出现了GDP 的增加。根据式(5)可知,从数值上看计算的Gci越大,说明在该子流域实施退耕还林操作后GDP 的损失越小,从经济角度上看就越适合进行退耕还林。表3中Gci值大于0 的子流域有34 和41,说明这些区域原有的耕地产生的经济效益较低,在这些子流域进行退耕还林能够在不降低区域GDP 水平的前提下降低流域出口的泥沙含量,那么这些子流域内的耕地应尽可能多地参与退耕还林。退耕还林导致的GDP 损失最严重的为子流域30,其Gci值为-5 756.83 元/km2,表明该子流域内每1 km2的退耕还林会使GDP 产值降低5 756.83 元。从地理位置上来看子流域30 位于信阳市市辖区附近,说明该区域内的耕地为当地居民的主要经济来源,具有极其重要的经济价值,盲目地实施退耕还林会带来较大的经济损失。除此之外,子流域4、11、15 和24 的Gci值均小于-1 000 元/km2,从地理位置上看这些子流域内聚集着桐柏县(子流域11)、信阳市(子流域4 和24)以及息县(子流域15)的主要居民点,因此在这些区域进行退耕还林时需要权衡经济损失和泥沙控制之间的平衡关系。
3.4 子流域退耕还林方案优化结果
遗传算法参数的选择对优化的最终结果有着一定的影响,为了确定合适的算法参数,对种群大小、迭代次数、交叉概率和变异概率这4 个参数分别进行敏感性分析。如表4 所示设定不同的参数变化情景,采用OAT(one-at-a-time)方法,即每次更改一个参数的值同时将其他所有参数值固定在初始值。各参数情景的优化结果如图5 所示。由图5a 可以看出当迭代次数从100 增加到600 时,优化出的Pareto 前沿逐渐向着两个目标函数的最小值逼近,但是当迭代次数增加到1 000 时,Pareto前沿并没有进一步被优化。图5b 中显示的种群大小大于以100 为分界线,种群大小超过100 得到的 Pareto 前沿明显优于种群大小为20 和50,当种群大小从200 增加到500 时Pareto 前沿在两个目标函数的寻优表现上并没有显著的提高。当交叉概率从0.1 增加到0.7,图5c 所示的Pareto 前沿也越来越优,但是当交叉概率进一步增加到0.9 时,Pareto 前沿出现了反向移动而变得更差。图5 d 中所示的变异概率设置为0.000 5 得到的Pareto 前沿与初始值0.000 1 较为接近,且都劣于其余设定值得到的Pareto 前沿。综合判断最终确定遗传算法的参数设定为:迭代次数600,种群大小400,交叉概率0.7,变异概率0.01。

图5 遗传算法参数敏感性分析结果Fig.5 Sensitivity analysis results of the genetic algorithm parameters
根据设定的遗传算法参数进行多目标优化,得到的Pareto 前沿图6 所示,构成了子流域尺度退耕还林多目标优化问题的最优方案集,该方案集一方面将GDP 损失控制在105 万元至196 万元,损失率为30.13%至37.67%;另一方面将流域的产沙量控制在63.5 万t 至97.9 万t,相较于基准期的泥沙产量分别削减了69.86%和53.54%。PIMENTEL[34]将土壤的形成速率0.5~1.0 t/hm2定义为区域可持续发展的土壤侵蚀水平,认为土壤侵蚀的速度若大于这一临界水平时,土壤有机体的多样性和丰富度会大幅度降低从而不利于该区域农业的可持续发展。据此标准换算出研究区息县流域可持续发展水平下的土壤侵蚀量为51.2~102.5 万t,不难看出对于优化出的Pareto前沿上的所有解均没有该水平的超过上限值,说明即使是在经济效益目标的牵制下,优化得到的退耕还林方案集的生态效益目标仍然能够达到较为满意的程度。
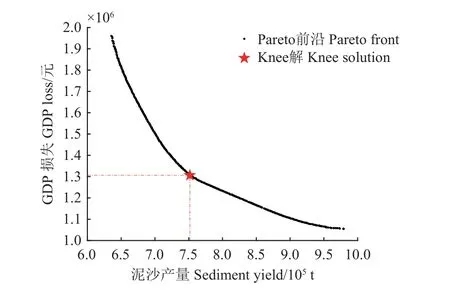
图6 多目标优化结果的Pareto 前沿及Knee 解Fig.6 Pareto frontier and Knee solution of multi-objective optimization results
退耕还林直接减少了粮食生产的基本物质基础,对区域粮食安全产生的影响不容忽视。人均耕地面积这一指标常被用来分析地区或区域的粮食安全问题。经统计得到Pareto 前沿解集中全流域的退耕面积为2 508.5~3 889.0 km2,根据研究流域所辖行政区统计年鉴统计研究流域的人口数量(2 753 960 人),由此计算退耕还林后剩余的人均耕地面积为1.04×10-3~1.54×10-3km2,均高于陈百明等[35]预测的近期人均耕地面积阈值0.74×10-3km2和远期人均耕地阈值0.64×10-3km2,说明本研究所求的退耕还林方案解集即使是减少了研究区耕地的面积也仍然能够满足人均粮食供给。另外,基于本研究构造的优化问题,即流域产沙量最小和GDP 损失最小,在优化算法求解的过程中会引导着退耕还林面积更多地偏向于土壤易侵蚀且耕地产值较低的区域配置。时亚坤等[36-37]的研究均强调,一方面退耕还林实施区的耕地质量差且粮食产量本就较低,另一方面耕地面积的减少促使农户从粗放式的生产模式转变为集约式,进而有效改善了区域环境和土壤肥力,因此可认为退耕还林的实施有助于提高粮食产量。综合分析来看,本研究求解的退耕还林方案集能够发挥水土保持和粮食供给的协同作用。
针对Pareto 前沿上的Knee 解(如图6 所示),在土地利用现状上确定全流域的退耕还林方案,如表5 所示按照子流域退耕还林面积百分比从大到小排列。可以看出上游子流域退耕还林面积比例一般较大,基本上都超过了50%。退耕还林面积占比最小的几个子流域(子流域19、30、4 和24)主要集中在信阳市辖区及周边。根据表5 统计全流域退耕还林总面积为2 988.87 km2,占现状土地利用耕地面积的44.19%。该退耕还林方案下对应的两个目标函数分别为泥沙产量75.1 万t 和GDP 损失130 万元,经计算可知该方案以牺牲约25%的经济损失换取了约65%的泥沙削减量。盛莉等[38]从土壤保持价值和涵养水源价值两个方面估算了中国水土保持的生态功能服务价值,在全国平均水平得出单位重量(t)的土壤保持量可提供58.96 元的生态服务价值。据此可以推断本研究中削减的泥沙量能够提供约7 994 万元的生态服务价值,远大于估算的GDP 损失值,因此可认为优化出的退耕还林方案对保护研究区生态环境有着巨大的潜力,具有较高的成本效益。

表5 Knee 解对应的子流域尺度的退耕还林面积Table 5 GGP area at sub-basin scale corresponding to the Knee solution
考虑到退耕还林工程需要面对退耕耕地种类和还林林地种类的选择,本研究遵循研究区自然规律,坚持因地制宜的原则:子流域内面积不占绝对主导的耕地类型优先参与退耕;若子流域内水田旱地面积相当,则根据淮河干流南北的气候差异,干流以北的耕地优先考虑退水田,干流以南的区域优先考虑退旱地;根据退耕区高程差异,高程800 m 以上种植落叶阔叶林,高程500~800 m 种植常绿阔叶林及落叶阔叶林,高程500 m 以下种植常绿针叶林及经济林。据此原则各子流域具体的退耕还林方式可分为五类:河源子流域11 内的水田零散分布且海拔较高,因此该子流域内优先退水田还落叶阔叶林;相邻的河源子流域26 内面积较少的水田优先退耕,退常绿阔叶林及落叶阔叶林;子流域10 和子流域36 分别位于桐柏县和信阳浉河区,面积不占主导的旱地优先退耕,还常绿阔叶林及落叶阔叶林;淮河干流以北的大部分子流域(1~9、12、13、16、18、19、21 和24)以及干流以南的部分子流域(25、27、35 和38)退水田还针叶林及经济林;位于淮河干流以南的剩余子流域则退旱地还常绿针叶林及经济林。
4 结论
本研究结合分布式水文模型模拟、空间叠置分析以及多目标优化方法,以流域泥沙产量和经济损失最小构造多目标优化问题,求解得到子流域退耕还林最优解集,并从中选取了最具成本效益的退耕还林方案。本文的主要研究结论有:
1) SWAT 模型径流模拟率定期(1996—2003 年)和验证期(2004—2010 年)的Nash 系数Ens均大于0.90,决定系数R2均大于0.90,百分比偏差PBIAS分别为-4.26%和-5.73%;对于泥沙模拟率定期和验证期的Nash 系数Ens均大于0.70,决定系数R2均大于0.80,百分比偏差PBIAS均控制在20%之内。由于本文在数据收集过程中受到一定的限制,只针对历史时期的径流和泥沙过程进行了模拟。但是考虑到研究区的气象和下垫面条件没有发生较大的突变,因此认为基于历史时期模型率定和验证得到的参数仍能够沿用到近期。因此,精度评定结果能够说明SWAT 模型对研究流域径流和泥沙的模拟具有较好的适用性。
2) 泥沙削减系数在空间上呈现出上游向下游逐渐减小的过渡趋势,说明在上游进行退耕还林操作能取得更好的泥沙控制效果。
3) GDP 损失系数其在空间上呈现出较大的差异性,在居民点聚集的区域进行退耕还林操作会带来较大的经济损失。
4) 子流域尺度退耕还林最优方案集能够在经济损失了30.13%~37.67%的同时将流域泥沙产量削减53.54%~69.86%,且能够平衡水土保持、经济损失和粮食供给三者之间的矛盾。同时,最具成本效益的退耕还林方案对应的退耕面积占总耕地面积的44.19%且主要集中于上游子流域,由此带来的泥沙削减率约为65%,经济损失约为25%。

