基于SHAP 重要性排序和机器学习算法的灌区渠道调度流量预测

葛建坤，雷国相，陈皓锐，张宝忠，陈来宝，白美健，苏 楠，于子慧

（1.华北水利水电大学水利学院，郑州 450045；2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100048；3.国家节水灌溉北京工程技术研究中心，北京 100048；4.安徽省淠史杭灌区管理总局，六安 237005）

0 引言

灌区渠道除接受上游水库/渠道的供水外，还可能接受沿程的坡面汇流、平交河道的洪水汇入，在暴雨条件下，渠道上游来流叠加沿程的各种面状（坡面洪水）和线状汇流（平交河道汇流），可能会导致渠道水位过高，影响渠道的安全运行，灌区泄水闸能够快速宣泄这部分洪水，确保汛期渠道安全。因此，如何合理的进行渠道泄水闸的决策是灌区管理者在汛期需要面对的问题。与自然流域洪水过程类似，渠道洪水的发生和推进也包括渠道沿程集水区的降雨产汇流过程和洪水在渠道中的演进过程；与其不同的是，渠道中节制闸、分水闸和泄水闸的人工调度会对洪水入渠后的推进过程有较大的影响，其边界条件较自然流域更为复杂，这也给合理开展渠道防洪调度带来了挑战。

基于物理机制的明渠/河道泄水需在摸清灌区渠道来水汇入点、沿程汇流集水区、泄水点和分水点的空间分布和水力拓扑关系的基础上，通过耦合产汇流模型、一维明渠水流运动和调度优化模型进行防洪调度决策优化。防洪调度是一个非线性复杂决策过程，这使得调度方案的优化决策难以实现[1-2]。基于物理机制的防洪调度优化方法主要分为线性规划（linear programming,LP）、非线性规划（non-linear programming,NLP）、动态规划（dynamic programming,DP）、鹈鹕优化算法（pelican optimization algorithm,POA）和遗传算法等。李其梁等[3]建立了基于线性规划的两湖河道联合调度数学模型，可为汛期洪水资源配置提供决策依据。非线性规划能够处理目标函数不可分和非线性约束问题，能够应用于更复杂的优化调度场景中，林瑜等[4]构建了基于马斯京根模型的非线性规划模拟河段渠道中的洪水演进过程，为汛期渠道断面流量决策提供了可靠的方法。但LP 和NLP方法不能考虑单个泄水闸的状态，因此不适合处理灌区渠道调度决策问题。ZHAO 等[5]将单调关系与动态规划进行合并，提出了改进DP 的新算法，该算法可以作为防洪调度的有用工具测试不同的洪水情景并确定最优决策。LIU 等[6]利用POA 方法确定了考虑河道优化的汛期多目标最优调度规则。但DP 和POA 计算工作量大，泄水闸数量较多时，容易造成“维数灾难”，需要一定的降维方法。AFAN 等[7]以尼罗河高阿斯旺大坝为研究对象，采用遗传算法优化了河流流量的预测精度，确定了时间序列下预测洪水的有效输入参数，研究结果可为其他类似地区的河道防洪调控提供参考。但遗传算法编程较为复杂，且算法内包含的交叉率、变异率等参数的设定依然需要人工经验确定。基于物理机制的防洪调度优化模型不仅在各环节的物理过程控制方程的求解和耦合方面较为复杂，而且涉及大量的模型参数，其实际应用过程中对数据资料的要求和模型使用者的专业要求较高。因此，如果能够基于影响渠道泄水决策的主要影响因素获得相对容易监测的数据，开展渠道防洪调度的决策，可以避免上述物理机制模型的缺点。

近年来，人工智能技术发展迅速，机器学习作为人工智能技术的核心分支，能够学习经验数据中输入和输出之间的复杂关系，快速提取高维数据特征和处理非线性数据，且具有良好的容错性[8]。高玮志等[9]利用机器学习解决了太湖流域多层次防洪调度方案的评价问题。张帆等[10]采用多种机器学习模型对洪水特征指标进行了评估，为防洪措施的制定提供了参考。尽管机器学习算法在先前研究中表现良好，但由于其特有的“黑箱”性质，无法解释各变量对预测结果的贡献程度。Shapley Additive exPlanations（SHAP）作为当前热门的机器学习事后解释工具，能够检测特征之间的交互作用，从而提供更加全面的特征重要性排序结果[11-12]。目前已用于环境监测、土地利用、信息科学等[11,13-14]重要领域，该方法能够清楚量化机器学习算法中特征变量的全局重要性，可为防洪调度中关键因素的识别以及机器学习算法优化提供重要帮助。

目前，灌区渠道防洪调度决策依赖复杂物理机制的调度优化模型，决策者需要对各渠段在不同暴雨条件下的来洪过程、洪量和洪峰大小、渠道的承洪能力、泄洪效果等非常了解才能做出较为合理的调度决策，若了解不充分，则可能造成渠道水量过度下泄等问题，危害下游渠系建筑物的安全。鉴于此，为给灌区渠道防洪调度决策提供一种简单高效的方法，本研究以安徽淠史杭灌区灌口集泄水闸为例，基于实测的闸上水位、历史和预报降雨信息以及泄水调度流量数据，比较不同机器学习算法的预测精度，同时采用SHAP 法筛选特征变量组合，进一步优化算法精度。以期为灌区现代化管理提供技术支撑。

1 材料与方法

1.1 研究区概况

淠史杭灌区位于安徽省中西部和河南省东南部，是中国特大灌区之一。其中安徽部分由淠河、史河、杭埠河三大灌区组成（图1）。灌区地貌包括山丘和平原两大类型，对于途经山丘区的渠段，在遭遇暴雨时，渠道一侧坡面的降雨产流会汇入渠道，引起渠道水位过高，从而引发渠道运行安全问题，该问题在南方丘陵灌区具有典型代表性。史河灌区位于淠史杭灌区西部，该灌区的局管渠道包括5 个泄水闸，渠道防汛调度以节制闸为界划分为4 个调度单元，各调度单元来洪基本在单元内排除。灌口集调度单元进口为看花楼节制闸，出口为河套汀渡槽，该单元有2 片侧向坡面来水，分别通过白嗒河和坡面散流进入渠道，单元内设置了灌口集泄水闸用于排除洪水。灌口集泄水闸单孔闸宽7 m，共5 孔，设计流量265 m3/s，闸上设计水位57.32 m。

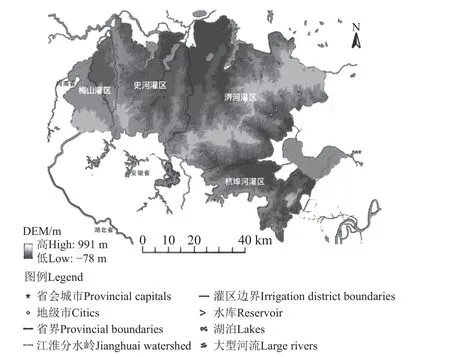
图1 淠史杭灌区示意图Fig.1 Schematic diagram of irrigation area of Pi Shihang

1.2 影响因素分析和数据来源

灌区渠道泄洪调度期间，对于特定的泄水闸而言，其所在渠道的集水区面积、土壤质地、下垫面条件、集水区坡面/入渠河道的地形和坡度、坡面或者入渠河道的糙率、渠道断面和坡度、渠道糙率等因素一般固定不变。灌区渠道在汛期关闭进水闸或分水闸时，渠道无上游来水，洪水完全来自单元流域内的降雨[15]。渠道水位是汛期灌区管理人员进行洪水调度时的首要关注指标，各泄水闸段的渠道水位不能超过警戒水位，防止漫顶[16]。通过咨询灌区管理部门可知，对于灌口集调度单元而言，当启动防洪调度时，单元进口闸（看花楼节制闸）关闭，即渠道上游来流始终为0，该单元沿渠也未受其他闸门影响（图2）。因此，灌口集泄水闸的调度方式主要取决于过去的落地雨量、未来预报的雨量以及泄水闸前的实时水位及动态变化量。为尽可能全面考虑泄水闸调度的影响因素，本研究选取过去1、2、3、6、9 h 和未来1、3、6 h 累积降雨量、灌口集泄水闸闸上水位和闸上水位差作为特征变量，以灌口集泄水闸调度流量作为目标变量（表1），其中降雨量以集水片区内部及其附近的8个降雨站点平均值代表面雨量（白塔畈、龚店、薛贩、万山桥、小高庙、朱小堰、红石嘴、梅山）。上述各类数据来源于安徽省水文局和淠史杭灌区管理总局。

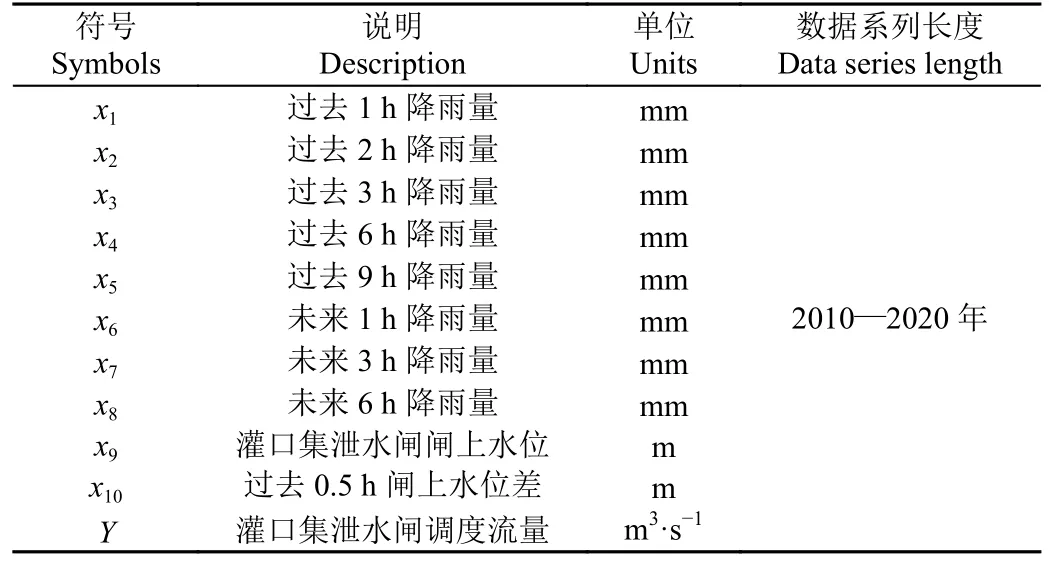
表1 变量及说明Table 1 Variables and descriptions

图2 灌口集泄水单元连接关系图Fig.2 Guan Kouji drainage unit connection relationship diagram

为检验特征变量是否能解释调度流量变化规律，对灌口集泄水闸调度流量Y进行分析。由图3 可以看出，调度流量分布曲线在偏度及峰度上与正态分布曲线均有一定的相似度，采用柯尔莫哥洛夫-斯米尔诺夫检验（kolmogorov-smirnov,K-S 检验）得到变量Y及x1～x10的P值分别为0.225、0.140、0.131、0.133、0.121、0.075、0.130、0.122、0.135、0.232、0.208（P＞0.05），均服从正态分布，参考文献[17]，将x1～x10全部用于算法预测及验证。

图3 灌口集泄水闸调度流量分布曲线Fig.3 Distribution curve of dispatching flow of Guan Kouji drainage gate

1.3 研究方法

本研究所用方法分为预测方法和特征变量筛选方法两大类，其中预测方法用来建立特征变量与调度流量之间的关系，特征变量筛选方法是在分析特征变量对调度流量预测结果的影响程度大小的基础上，筛选变量组合。预测方法选取了线性回归（linear regression,LR）、K 近邻回归（k-nearest neighbors regressor,KNR）、岭回归（ridge regression,RDR）、决策树回归（decision tree regression,DTR）4 种传统回归算法和支持向量回归（support vector regression,SVR）、自适应提升回归（adaptive boosting regression,ABR）、极度梯度提升回归（extreme gradient boosting,regression,XGR）、随机森林回归（random forest regression,RFR）4 种集成学习算法进行比较。传统回归算法中LR 可判断变量与目标因子之间线性相关程度的强弱[18]。KNR 适宜对连续时间的数据进行预测[19]，符合本研究的数据类型。RDR 能够处理自变量间多重共线性问题[20]。DTR 能够表现数据间复杂的非线性关系，对缺失值不敏感且训练速度较快，适合用于小规模数据集的回归预测[21]。集成学习算法能够串联传统机器学习算法中的多个基学习器，提高预测性能。本文采用的4 种集成学习算法可分为3 类，其中SVR 和RFR 分别属于堆叠算法（stacking）和装袋算法（bagging），ABR 和XGR 属于提升算法（boosting）。Stacking 集成的高层模型使用线性回归等基学习器进行组合输出[22]，bagging 使用同质弱学习器，其输出投票或平均产生，最终获得比基学习器更小的方差；boosting串联各个基学习器调整样本的损失函数或权重，通过叠加来减少总模型的预测偏差[23]。其中ABR 和XGR 在拟合残差方式上有所不同。8 种机器学习算法的关键参数及说明见表2。

表2 算法参数及说明Table 2 Algorithm parameters and description

采用SHAP 法对特征变量进行筛选。SHAP 法能够提供多特征交互影响下各个特征对于预测结果的贡献值[11]。将x1～x10作为特征变量，Y作为目标变量，对8种机器学习算法预测精度进行比较并挑选出最优算法，再利用SHAP 法对特征变量进行筛选组合，确定最终的调度流量决策模型（图4）。各方法及说明见表2。

图4 研究技术路线Fig.4 Technology roadmap of this study

1）LR 算法

线性回归算法用于确定两个及多个变量之间定量关系[18]，通用计算式为

2）KNR 算法

K近邻回归算法采用测量特征值之间距离的方法进行预测[19]，样本的回归预测输出值为

式中wv为样本权重，S为训练样本数，yv为第v个样本的输出值。

3）RDR 算法

岭回归是一种专用于处理共线性数据的回归方法[20]，一般回归分析的(矩阵)形式如下：

式中X为输入变量矩阵，β为回归系数矩阵，ε为误差矩阵。

4）DTR 算法

在机器学习中，决策树表示对象属性与其值之间的映射[21]。将输入空间划分为M 个区域R1，R2，……，RM，选定的划分区域相应输出函数为

式中M为区域个数，Rm为第m个区域空间，j为区域中的输入变量，ym为区域Rm的目标变量输出值。

5）SVR 算法

支持向量机用于回归问题时寻求二分法以最小化到超平面最远样本点的“距离”[24]，遵循使用核技巧转换数据的技术找到最佳输出边界。位于边界得到内的点满足：

式中w为权向量，a为输入变量，∅ (a)为高维特征空间，c为偏置常数。

6）ABR 算法

ABR 采用迭代思想，分类输出取决于这些多个分类器的组合效果[25]。构建的最终强分类器为

式中ht为基学习器，αt为每个基学习器的权重系数，T为基学习器个数，g为输入变量。

7）XGR 算法

XGR 是一种基于CART（classification and regression tree）的Boosting 类集成学习模型[26]，其目标函数为

8）RFR 算法

随机森林回归是一种基于决策树的集成学习算法[27]，包含层次上的的随机性，进行回归预测时，从所有的特征输入值H中随机选择h个值构建每棵决策树，从这h个值中去选择优化每个分割节点时，从而降低相关性，提高预测能力。

9）SHAP 法

SHAP 是一种将传统方法与博弈论和局部解释联系起来，根据预期表示一致性和局部准确性的特征归因方法[11]。SHAP value 为样本中特征的分配数值，满足等式：

式中Yn为输出的SHAP 值，yb为所有样本目标变量的均值，f(xn,1) 为第n个样本中第1 个特征变量对该样本预测的贡献值，f(xn,P) 以此类推。

1.4 数据标准化与算法评价指标

将搜集到的180 组变量数据按照4:1 的比例分为训练集与测试集，调用Python 3.9 进行算法预测与验证。

1）为消除数据量纲对于研究效果的影响，模型数据采用Z-score 标准化方法，其计算式如下：

式中ZB表示标准化后的数值，Z表示原始数据，Z表示原始数据的平均数，σ 表示原始数据的标准差。

2）为评估算法预测精度，利用灌口集泄水闸调度流量预测值与实际值之间的均方根误差（SRMSE）、平均绝对误差（SMAE）、均方误差（SMSE）和决定系数（R2）作为评价指标。其中SRMSE、SMAE和SMSE越接近0，表示模型偏差度越小；R2越接近1，表明预测值与实际值之间的吻合度越高。具体计算公式如下：

式中Rk为第k组数据的实际调度流量值；Pk为第k组数据的预测调度流量值；R为Rk的平均值；P为Pk的平均值；F为样本个数。

2 结果与分析

2.1 基于不同机器算法的调度流量预测精度比较

为了验证8 种机器学习算法在整个数据集上是否适用，本研究同时对训练集和测试集进行预测，分析其SRMSE、SMAE、SMSE及R2指标并进行比较（表3）。

表3 基于8 种算法的调度流量预测评价Table 3 Prediction evaluation of dispatching flow based on 8 algorithms

由表3 可得，传统回归算法中DTR 训练集及测试集误差指标均为4 种算法中最优，LR 的训练集SMSE较最大的KNR 仅降低了6.6%，其余指标均为4 种算法中最差。因此，LR 在传统回归算法中的预测精度最差。集成学习算法中SVR 训练集及测试集SMAE较最大的ABR 分别降低了0.7%、5.3%，降幅不大，其余指标均为4 种算法中最差。因此，SVR 在4 种集成学习算法中的预测精度最差。对比SVR 和DTR，SVR 训练集及测试集误差指标均优于DTR。综上，集成学习算法较传统回归算法预测精度更佳。集成学习算法间的预测精度也具有一定差异，RFR 训练集SRMSE、SMAE、SMSE、R2分别为0.146 m3/s、0.094 m3/s、0.021 m3/s、0.976；测试集分别为0.306 m3/s、0.197 m3/s、0.093 m3/s、0.931，在集成学习算法中RFR 的预测精度最高。DTR 训练集SRMSE、SMAE、SMSE、R2分别为0.476 m3/s、0.324 m3/s、0.227 m3/s、0.724；测试集分别为0.511 m3/s、0.381 m3/s、0.261 m3/s、0.808，相比DTR，RFR 的预测精度更高。

对比4 种集成学习算法，XGR 在训练集及测试集误差指标上均优于ABR，RFR 的训练集SMAE与XGR 相差不大，其余指标均优于XGR，集成学习算法的预测精度排序为：RFR＞XGR＞ABR＞SVR，3 类集成学习算法的预测精度由高到低依次为装袋算法、提升算法、堆叠算法。综上，随机森林回归（RFR）在8 种算法中的预测精度最优（训练集SRMSE=0.146 m3/s、SMAE=0.094 m3/s、SMSE=0.021 m3/s、R2=0.976，测试集SRMSE=0.306 m3/s、SMAE=0.197 m3/s、SMSE=0.093 m3/s、R2=0.931）。

2.2 变量筛选优化

2.2.1 特征变量重要性分析

机器学习算法中，特征重要性是指特征变量对目标变量的影响程度，特征的选择对机器学习算法预测精度有较大影响，数量过多和不足分别会产生过拟合、欠拟合的问题，模拟精度均无法达到最佳。为检验采用10 组变量进行随机森林回归算法预测是否出现过拟合现象，本研究对10 组变量进行重要性分析（表4），得到不同变量对于预测结果的影响权重，通过比较不同变量组合下随机森林回归算法预测误差指标，挑选最佳变量组合进一步优化算法。

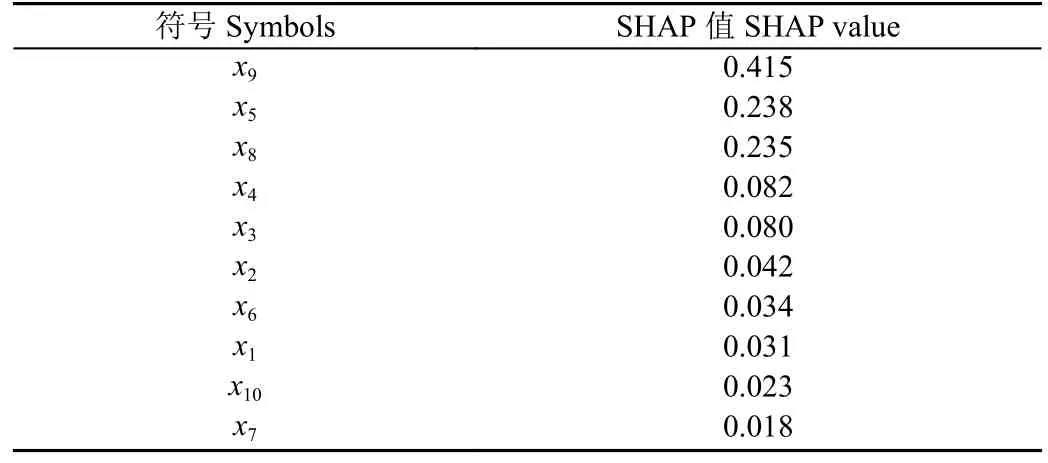
表4 SHAP 法特征重要性分析结果Table 4 Results of features importance analysis of SHAP method

由表4 得SHAP 法确定的变量组合特征重要性排序为：x9＞x5＞x8＞x4＞x3＞x2＞x6＞x1＞x10＞x7，x9对预测结果的影响最大，占SHAP 值总和的34.6%。过去时段降雨量（x1～x5）SHAP 值总和为0.473，未来时段降雨量（x6～x8）SHAP 值总和为0.287，可见过去时段降雨对泄水调度决策的影响程度比未来降雨更大。

2.2.2 特征变量筛选

根据表4 建立10 种组合分析训练集和测试集误差指标及变化趋势（表5）。由表5 可以看出，不同变量组合下，RFR 训练集SMSE、SMAE、SRMSE及R2均优于测试集，依次去除特征重要性最小的因素，误差指标SRMSE、SMAE、SMSE呈现出先减小后增大的趋势，R2呈现出先增大后减小的趋势。可见，当把x1～x10作为输入变量时出现了过拟合现象，变量组合x4+x8+x5+x9训练集及测试集指标均为10 种组合最优，由SHAP 法确定以x4+x5+x8+x9作为输入变量时，随机森林回归（RFR）算法的预测效果最佳（训练集SRMSE=0.126 m3/s、SMAE=0.080 m3/s、SMSE=0.016 m3/s、R2=0.982；测试集SRMSE=0.263 m3/s、SMAE=0.164 m3/s、SMSE=0.069 m3/s、R2=0.950）。其训练集及测试集R2较采用所有特征变量预测分别提高了0.6%、2.0%；SRMSE、SMAE、SMSE分别降低了13.7%、14.9%、23.8%、14.1%、16.3%、25.8%；可见变量选择对预测精度的影响较为显著。

表5 基于SHAP 法和RFR 的10 种组合训练集及测试集评价指标Table 5 Evaluation metrics for 10 combined training sets and test sets based on SHAP method and RFR

3 讨论

3.1 目标变量影响因子分析

本研究选择的10 个特征变量可归类为水位和降雨2种类型。LONG 等[28]指出，水位波动对三峡大坝的日调节流量影响较大；JANE 等[29]也提出，水位流量关系是分析洪水成因，进行风险评估的重要内容；纪亚星等[30]认为不同降雨重现期对理想区域的洪峰流量削减率不同；崔春光等[31]将中尺度数值模式的预报降雨信息输入新安江模型，结果表明预见期内的降水量直接影响洪水流量预报的精度，以上研究均表明水位和降雨是影响流量的重要因素。由表4 可得，在特征变量重要性排列中第一位为x9，其原因为闸上水位是影响灌口集泄水闸调度流量的直接因素，闸前水位高，其泄水流量必然趋向增大。降雨是诱发洪水的驱动因素和激发条件[32]，本研究中不同时段降雨量对泄水调度流量的影响不同，这与鲁洋等[33-34]研究一致。表4 中过去时段降雨对泄水调度决策的影响程度较未来降雨更大的原因是落地雨除去损失后的净雨为产流过程，未来降雨形成的径流过程需净雨通过坡面和沟道产生，降雨先后经历该2 个过程的变化，使径流的相关性弱于产流[35]。

3.2 不同机器学习算法预测精度差异

从表3 看出，集成学习算法误差指标明显优于传统机器学习算法，这是因为传统机器学习算法中各类基学习器在不同数据源上的学习效果不同，单一基学习器对于样本的学习误差可能较大。集成学习能够训练多个基学习器模型，得到一个较好的集成模型，从而提高整个模型的泛化能力[36]，由于基学习器的种类、训练模式以及输出方法不同，集成学习算法的预测结果也不尽相同。由表3 得到3 类集成学习算法中装袋算法预测精度最高的原因是：特征变量和目标变量分布趋势较为相似，装袋算法对于训练模型差距不大的样本，能够通过投票或平均化最大程度还原目标值。赵敬涛等[23]采用3 类集成学习算法对企业自律性进行评估，得到预测精度由高到低依次为：提升算法、装袋算法、堆叠算法，与本研究有所不同，这是因为：企业自律性评价数据集同时存在离散类和连续类特征，装袋算法的各个基学习器的输出只作一个简单的投票或平均，其学习效果有相当大的局限性[37]。而提升算法中梯度提升决策树（gradient boosting decision tree，GBDT）的每个分类器都会在上一轮训练基础上不断降低偏差，对于多特征数据集学习效果更佳。同时，赵敬涛等得到XGR 预测精度优于ABR，与本研究结果一致，这是因为：ABR 通过拟合残差逐渐减少残差，而XGR 基于GBDT 的每次计算都能减少残差，XGR 较ABR 可更大程度上减少误差。

本研究对比8 种机器学习算法预测评价指标，随机森林算法预测精度高于其他算法的原因可能是：1）现有的随机森林算法不需要考虑一般回归问题所面临的多元共线性问题，在部分数据缺失或数据量相对较小的情况下仍能保持一定的精度[38]；2）随机森林算法具有一定的抗噪声能力；3）时间、降雨、水位及流量间的数据维度相差较大，随机森林算法无需做特征选择，对数据集的适应能力强。HASAN 等[39]以沿海地区为例，研究得到随机森林算法能够准确预估洪水敏感性，为防洪策略制定提供了可靠思路；高玮志等[40]基于KNN 和随机森林算法构建流域、区域、城镇多层次调度方案综合评价模型，为防洪调度方案的优选提供科学参考。以上研究结果均证实了随机森林算法在防洪调度决策上的可行性。

3.3 特征变量筛选对预测精度的影响

机器学习算法模拟精度受数据集特征选择的影响[41]。STEPHEN 等[42]认为合理的特征选择可以消除数据中的噪声，提高模型性能。本研究采用SHAP 法对所选10 组特征变量进行重要性排序，并分为10 种组合进行预测对比，结果表明，采用x4+x5+x8+x9作为输入变量时，随机森林回归算法预测精度最佳。同时，选用x4+x5+x8+x9相比于选用全部变量也降低了数据收集成本和难度。综合2010—2020 年历史数据，过去6 h 降雨量、过去9 h降雨量、未来6 h 降雨量、灌口集泄水闸闸上水位是影响灌口集泄水闸调度流量的主要因素。

本研究基于机器学习构建的泄水调度决策模型，属于数据驱动型的黑箱模型，与相关的产汇流—洪水演进—泄水调度耦合性机理模型在本质上有较大区别，两者各有其优缺点，机理模型虽然能够得到诸如入渠洪水流量过程、渠道及洪水位演进等中间要素的动态变化，但其需要的水文水动力方程耦合计算过程较为复杂；机器学习虽无法得到相关水文演进过程，但其主要优点在于能够利用降雨和水位等相对易获取的监测和预报数据，快速地获取泄水闸的调度决策方案，避免了耦合机理模型所需要的多源数据搜集和预前处理。

4 结论

本研究基于安徽淠史杭灌区灌口集泄水闸调度流量及闸上水位和降雨数据，采用4 种传统机器学习回归算法（线性回归（linear regression,LR）、K 近邻回归（knearest neighbors regressor,KNR）、岭回归（ridge regression,RDR）、决策树回归（decision tree regression,DTR））和4 种集成学习类算法（支持向量回归（support vector regression,SVR）、自适应提升回归（adaptive boosting regression,ABR）、极度梯度提升回归（extreme gradient boosting regression,XGR）、随机森林回归（random forest regression,RFR））进行预测对比，并通过SHAP 法进行特征重要性分析，得到结论如下：

1）集成学习算法预测评价指标优于传统回归算法，8 种机器学习算法中RFR 的预测精度最高（训练集均方根误差、平均绝对误差、均方误差及决定系数分别为0.146 m3/s、0.094 m3/s、0.021 m3/s、0.976，测试集分别为0.306 m3/s、0.197 m3/s、0.093 m3/s、0.931）。

2）采用Shapley Additive exPlanations（SHAP）法确定的特征变量重要性排序表明灌口集泄水闸闸上水位对于泄水闸调度流量的预测结果影响最大，占特征重要性值总和的34.6%。

3）以过去6 h 降雨量、过去9 h 降雨量、未来6 h降雨量、灌口集泄水闸闸上水位为输入变量的随机森林回归算法预测灌口集泄水闸调度流量效果最佳，模型误差指标为（训练集均方根误差、平均绝对误差、均方误差及决定系数分别为0.126 m3/s、0.080 m3/s、0.016 m3/s、0.982；测试集分别为0.263 m3/s、0.164 m3/s、0.069 m3/s、0.950）。

本研究的不足之处在于采用SHAP 法和随机森林算法构建的调度流量预测模型是针对灌区渠道特定闸门的决策模型，在考虑因素时候只选取了不同时期的降雨和水位。因此，若要将其推广至更大的下垫面区域，后续研究应将更多的变动影响因素（如流域下垫面面积、河道断面糙率、渠道断面坡度等）纳入考虑。