淤地坝泥沙淤积高度对宽顶堰水力特性的影响
张家璇,李永业,宋晓腾,陶思远
(太原理工大学水利科学与工程学院,太原 030024)
0 引言
淤地坝是用于中国黄土高原沟壑区沟道治理的一种水土保持工程,其在拦泥、滞洪、减轻沟道侵蚀、促进农业生产等方面具有重要作用[1-5]。然而早期由于缺少科学设计,技术落后等因素,导致现有部分淤地坝面临坝体受损[6],泄洪能力不足[7],泥沙淤积超出库容[8]等问题,需要对病险坝进行除险加固措施。
针对目前淤地坝存在的问题,国内学者已经提出多种改造方案。如推广低成本、适应性强的柔性溢洪道[9];设置高强度防冲刷保护层以实现坝顶溢流[10];利用黏土斜墙、土工膜进行防渗改造[11]等。由于随着运行时间的不断延长,不少淤地坝的坝地已经淤满或接近淤满[12],坝内不同高度的淤积面将对洪水泄流过程、水沙的阻控过程产生较大影响[13]。在泥沙研究方向,一些学者从坝地泥沙来源[14-15],泥沙淤积分布特性[16]来推求其对淤地坝减蚀作用的影响。在水动力研究方向上,段金晓[17]对比了淤地坝不同淤积程度下沟道径流能量和径流侵蚀功率等参数,阐明了淤积对沟道侵蚀阻控作用的影响。白雷超[18]对比了淤地坝与下游沟道不同连接形式,即对比不同泄洪建筑物时的实际淤积情况,得到相应条件下单坝的拦沙泄流效益。其他学者也从坝型组合[19]、坝系连通方式[20]、暴雨径流[21]、植被覆盖[22]等角度对淤地坝洪水径流过程进行了研究。
然而,上述研究均未涉及“淤满”状态下的溢洪道泄流过程。对于多数使用年限久远的淤地坝,目前坝内的淤积面已经超过了溢洪道的渠底高程,同时伴随着泥沙迁移大量泥土在溢洪道内持续堆积,导致其原有的水力特性发生较大变化。为此,本研究以实际工程中常采用的宽顶堰式溢洪道为主体,通过物理模型试验研究“淤满”条件下不同淤积高度对溢洪道泄流的影响,分析其水力特性并率定流量系数,以为后续的除险加固工程提供参考。
1 宽顶堰过流的水力特性及流量系数
1.1 水力特性
宽顶堰作为溢洪道中的溢流结构,具有抬高水位和宣泄流量的作用。渠道中的水流经过堰顶时,流线急剧变化,堰流的流态、水面线、流速等水力特性会发生较大变化,直接关系到建筑物的结构安全和过流能力。宽顶堰过流相关的特征参数如图1 所示。

图1 宽顶堰过流的特征参数Fig.1 Characteristic parameters of overflow of broad crested weir
为探究流量Q与各个特征参数的关系,需对以下指标进行测量计算:
(1)自由出流
当宽顶堰的下游水位较低不影响堰的过流能力时为自由出流,通常采用如下判别条件:
(2)弗劳德数Fr
水力学中常用弗劳德数作为判别明渠流动特性的指标:
式中v为断面平均流速,m/s,g为重力加速度,m/s2,为断面平均水深,对于矩形明渠即为断面水深,m。
(3)堰上水头
堰上水头即上游水位超出堰顶的水深,能够反映宽顶堰的壅水程度。而在测量上游水深时,需满足测点位置距离堰壁上游大于3~5 倍堰上水头的要求。
1.2 宽顶堰流量系数影响分析
堰前淤积的存在会改变宽顶堰过流的水力特性,进而改变流量系数的取值,故采用量纲分析法推导淤积工况下流量系数m0的计算公式。宽顶堰的流量系数取决于其进口形式、几何结构、水流性质等[23],如式(3)所示。
式中Q为流量,m3/s;B为宽顶堰宽度,即溢洪道宽度,m;g为重力加速度,m/s2;σ为表面张力系数,N/m;μ为动力粘滞系数,N·s/m2,ρ为水的密度,kg/m3。
根据π 定理,选取H0,g,ρ为基本量纲,得到无量纲数关系式为
参考水力学中的堰流公式[23],使流量Q与堰上总水头的1.5 次方成比例,将公式(4)变形为
故堰流公式可以写为
其中流量系数m0为
由于表面张力项与黏性项对过堰水流的影响很小,在实际工程应用中忽略不计。在确定宽顶堰几何结构的前提下,即δ、B、P为常数时,引入相对淤积高度S/P来分析其对流量系数m0的影响。
2 模型设计与试验方案
2.1 模型设计
模型设计时参考了实际淤地坝工程的布置形式,即溢洪道布设于土坝右岸,进口采用弧形翼墙,控制段采用宽顶堰溢流,后接光滑陡槽与下游沟道连接。具体工程布置形式及尺寸如图2 所示。为了便于观测,物理模型采用有机玻璃组装搭建。在综合考虑场地因素、能耗限制及试验工况后,设置模型的几何比尺λL为14.8,依据重力相似准则计算得到流量比尺:=842.66,流速比尺:=3.85 及糙率比尺=1.567。溢洪道混凝土表面糙率为0.014,对应模型糙率为0.008 93,而有机玻璃约为0.009,可以满足试验要求。模型渠道总长6.3 m,其中渐变段翼墙0.68 m,控制段长1.35 m,宽顶堰固定于入口1.3 m 处。上游坝地延伸至模型的溢洪道进口前1.3 m 处,以获得平稳的进水条件。堰后陡槽水平长度为3 m,可以展现出宽顶堰完整泄流形态。堰前淤积采用固定木板代替,通过调整可以更改为不同的淤积高度。具体模型装置如图3 所示。
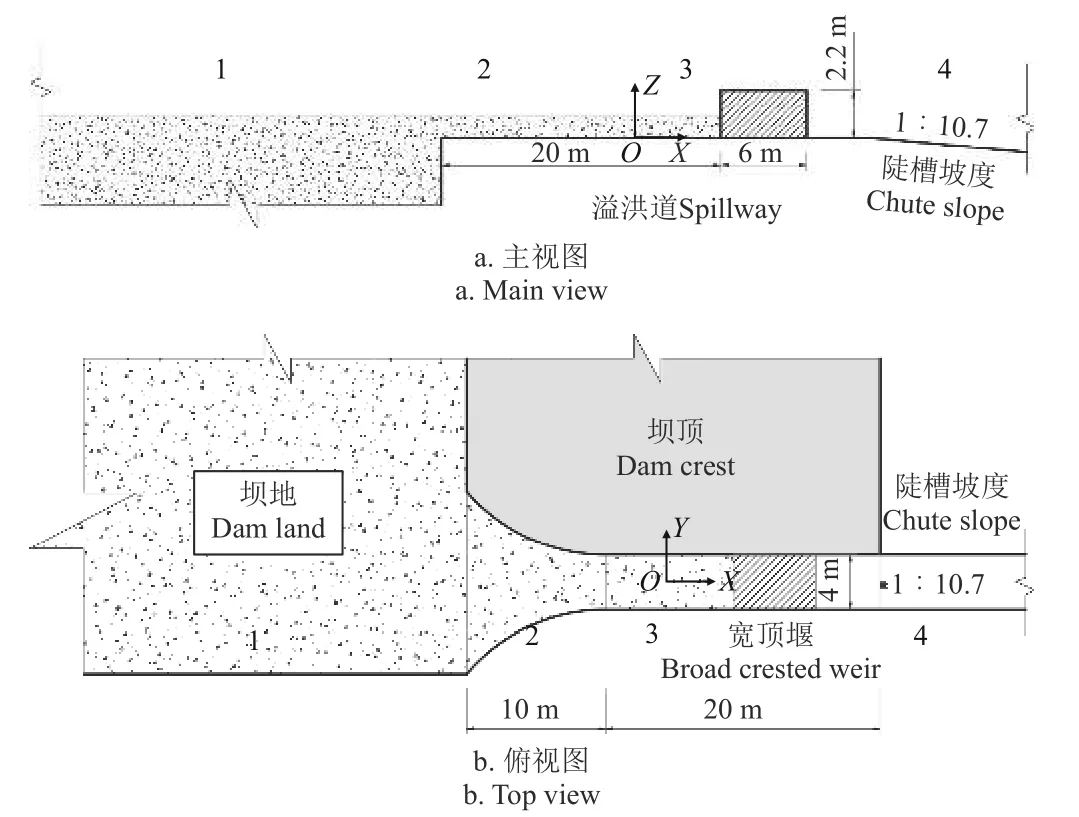
图2 淤地坝工程布置示意图Fig.2 Engineering layout diagram of check dam

图3 模型试验装置Fig.3 Model test facility
试验系统由地下水库、进出水管路、进出水箱、水泵、电磁流量计、调节阀门、溢洪道模型等组成,如图4 所示。水流由水泵从地下水库中抽出流入进水箱,通过稳水格栅使水流平稳进入后续模型试验段内。水流依次经过试验模型的溢洪道进口上游、溢洪道内宽顶堰部分、陡槽等模型后进入出水箱内,由出水管道进入地下水库,形成循环试验系统。

图4 试验系统Fig.4 Experimental system
2.2 试验方案与方法
为研究过堰水流的水力特性,在宽顶堰所在位置及其上下游选取15 个断面进行水深测量。在距堰壁上游30 cm 处水位尚未发生变化,故作为1 号测量断面。在堰后25 cm 处下游水位已经平稳,作为15 号测量段面。在堰顶水深急剧变化区域每隔5 cm 布置一条测线,可以完整呈现泄流形态。在每个测量断面上等距选取5 个流速测点,分别测量水流的底部、中部、表面3 个点的流速。为了更好描述水流的测量结果,选取1 号测量断面的渠底中心为坐标原点,X方向为水流方向,Y方向垂直于水流方向,Z方向竖直向上。具体测量断面、测点布置如图5 所示。

图5 水深、流速测点布置图Fig.5 Layout of water depth and flow velocity measuring points
试验固定堰高P为15 cm,设置5 个淤积高度工况,分别为0、30%P、50%P、70%P、90%P,即0、4.5、7.5、10.5、13.5 cm。结合一般淤地坝工程的洪峰流量和模型比尺,试验设置流量范围为20~90 m3/h。试验过程中,通过观测电磁流量计数值来调节阀门至待测流量,电磁流量计精度为0.1 m3/h;待水流稳定后,采用水位测针测量断面水深,精度为0.1 mm;采用旋桨式流速仪测量流速,精度为0.01 cm/s。
3 结果与分析
3.1 不同淤积高度对流态的影响
图6 为不同流量、淤积高度工况下的部分堰流流态。从图6 可以看出:在宽顶堰上游,水面稳定平缓,水流流态为均匀流。靠近堰顶位置水深逐渐下降,并在堰的进口附近呈现出一个收缩水深,水流流态为渐变流。在宽顶堰的顶托作用下,水位降低后形成一段与堰顶平行的水面线。由于溢洪道控制段后接陡槽,水流在堰后形成水舌,继而倾泻到下游渠道中,该部分为急变流。在小流量低水头工况下,整体水流平顺,水舌较薄并脱离堰壁,在堰后形成空腔。而随着流量的增加,水位整体抬高,水舌逐渐变厚,与下游水位衔接更加顺畅。而淤积高度的增加使得上游与堰顶的水位差下降,如在淤积高度达到90%堰高的情况下,堰坎对水流的阻碍作用很小,堰前水流壅水高度下降,水面线更加平缓,整体流态已趋近于明渠流动,该现象在小流量工况如Q=20 m3/h 较为明显,但同一淤积高度时随着流量的增大,堰前水位壅高逐渐增加,水流整体呈现为降水曲线。

图6 不同流量Q 及淤积高度S 下的堰流流态Fig.6 Flow pattern under different flow rate Q and siltation height S
3.2 不同淤积高度对水面线的影响
水面线可以直观体现堰前淤积对溢洪道过流的影响。图7 为不同淤积高度时的堰流沿程水面线变化曲线。从图7 可以看出,淤积高度对堰流水面线的影响主要集中在宽顶堰上游的壅水段(测量段0~30 cm 区间内)。该部分水位平缓,淤积面抬升了上游渠底高程,削弱了堰坎对水流的阻碍作用,使得壅水水深随着淤积高度的增加而降低。在堰顶及其下游段(30~95 cm 区间内),水流通过堰坎后急剧下降,水深主要与宽顶堰厚度以及下游渠道坡降相关,故各个工况下水面线基本一致,不受淤积高度的影响。因此,着重选取堰顶及其上游水位进一步计算分析。

图7 不同淤积高度下堰流沿程水位Fig.7 Water level along the flow at different siltation heights
以流量Q=20 m3/h 为例,在相对淤积高度S/P分别为0、30%、50%、70%、90%时,相邻淤积高度测量断面(堰前30 cm 处)的水位分别降低0.17、0.18、0.11、0.22 cm,相应的变化率分别为0.81%、0.86%、0.53%及1.06%。
当流量Q=70 m3/h 时,相邻淤积高度测量断面(堰前30 cm 处)的水位分别降低0.55、0.80、0.72、0.61 cm,相应的变化率分别为1.99%、2.95%、2.73%及2.38%。利用实测水深计算得到上游弗劳德数的沿程分布,如图8 所示。

图8 不同淤积高度下的弗劳德数Fr 沿程分布Fig.8 Distribution of Fr at different siltation heights
同一工况下,宽顶堰上游水流的Fr基本不变,流经堰顶区域后,Fr逐渐增大并达到1,即在堰顶出现临界水深。相同流量时,随着淤积高度的增加,宽顶堰上游Fr增大。尤其在淤积高度达到90%P时,Fr已接近0.5,堰流由缓流逐渐向急流转变。以上分析表明:淤积高度的增加使上游水位略微降低,过水断面面积增大,断面平均流速加快。且随着流量增大,该影响的程度增加。因而在实际工程中,溢洪道原设计的边墙高度可以适用于淤积工况。
3.3 不同淤积高度对流速的影响
渠道水流流速沿横向分布遵循指数流速分布规律,核心区边界距边壁距离很近,渠道中央的流速趋近于一个定值[24]。故流速采用同一测线上5 个测点的平均值分析,图9 为不同工况下的水流流速分布图。从图9 可以看出:各淤积工况下的堰流流速分布规律大致相似。在水流方向上,除堰的上游边界位置处(测量断面3,5)有流速激增的情况外,整体呈现平稳上升的趋势。在垂直方向上,各断面垂向流速符合对数规律,表面和中部流速略大于底部流速。同一流量工况下,在堰前位置处(测量断面1,2,3)流速随着淤积高度的增加而增加,主要是由于随着淤积高度的增加导致渠道底面高程被抬高,进而过流断面水深减小,水流在堰坎前的壅水范围变小,流速进而加快。
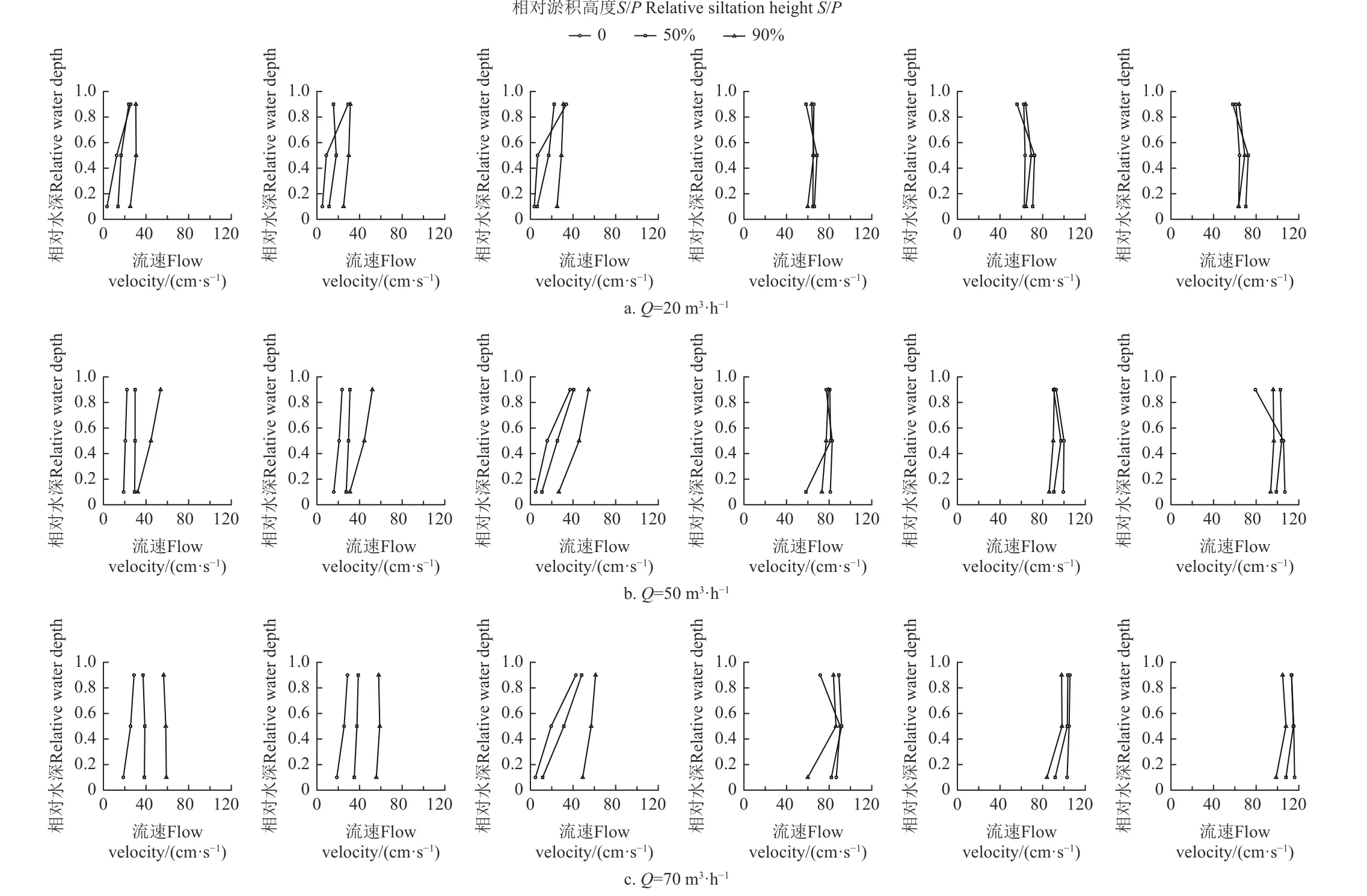
图9 不同淤积高度下的水流流速分布图Fig.9 Distribution of water flow velocity at different siltation heights
在堰顶进口以及堰后位置处,水流由渐变流转变为急变流,水位降低流速急剧增大。综上,淤积高度的变化对堰流沿程流速的影响范围主要集中在堰前位置处,其流速随着淤积高度的增加而增加,而对堰顶及堰后水流流速的影响幅度较小。根据土壤侵蚀相关理论可知[25],溢流堰前的淤地面流速增大,其受到的径流剪切力以及洪水的携沙能力均增强,不利于发挥淤地坝的拦沙减蚀效益。
3.4 宽顶堰流量系数分析
堰上水头反映了宽顶堰引起的壅水程度,与流量的大小存在对应关系,试验需要测量堰上水头来计算流量系数。图10 为5 种淤积高度下堰上水头H与流量Q的关系。由图可知,在任一流量下随着淤积高度的增加,堰上水头减小,即堰前壅水程度减小,宽顶堰的过流能力增强。

图10 堰上水头H 与流量Q 关系Fig.10 Relationship between hydraulic head over the weir H and flow rate Q
在实际运用中为了便于计算流量,直接使用堰上水头H代替堰上总水头H0,忽略行进流速的影响[23]。在流量Q、堰顶水头H、堰宽B均已知的情况下,可利用式(6)反推得到流量系数m0的实测值。图11 为不同淤积高度S/P时流量系数m0与P/H的关系曲线。由图可知,在固定堰形条件下,随着堰上水头H的增加,流量系数m0会略微增大,符合堰流的一般规律。而随着淤积高度的增加,流量系数m0整体增大,宽顶堰的过流能力增强。
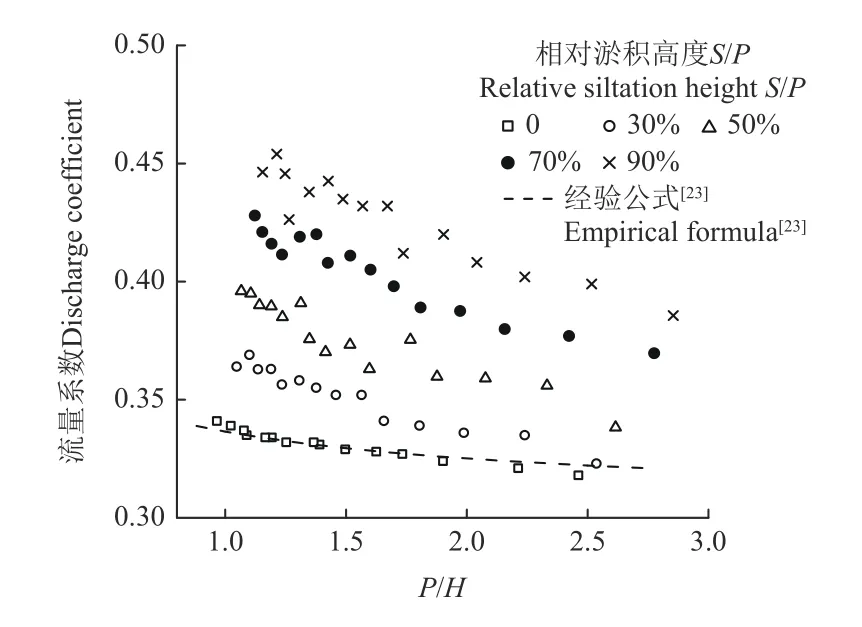
图11 流量系数m0 实测值Fig.11 Measured value of discharge coefficient m0
对于进口底坎边缘为方角时宽顶堰的流量系数m,已有如下经验公式[23]:
上式适用于0≤P/H≤3。当P/H>3 时,m可视为常数,取0.32。
将式(8)中流量系数m与P/H对应关系绘制于图11中,与流量系数实测值进行比对,结果显示,除未淤积S=0 时试验所得流量系数与传统经验公式(8)有较高的吻合度外,其余情况下两者误差较大。故在实际工程中,采用式(8)会使流量计算值偏小,已无法适应淤积的影响。所以基于一致性和适用性的原则[26-27],引入参数相对淤积高度S/P,参照公式(8)的形式拟合得到了存在淤积条件下的流量系数m0的计算公式为
式中α=S/P。
将不同工况下流量系数m0的计算结果代入式(6)得到流量Q的计算值,并与实测值对比,结果如图12所示。二者最大相对误差为7.4%,平均相对误差为2.7%,能够满足流量计算的精度要求。
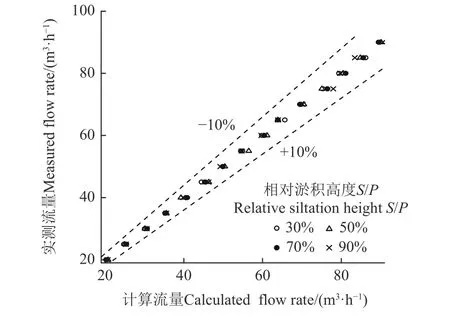
图12 流量实测值与计算值误差图Fig.12 Error diagram of measured value and calculated value of flow rate
4 结论
本文针对淤地坝除险加固工作中,“淤满”坝的泥沙漫延至溢洪道内宽顶堰处的问题,利用物理模型试验的方法对宽顶堰前存在泥沙淤积时的堰流水力特性进行研究。结果表明:
1)堰前淤积会改变溢洪道内整体水流形态。随着淤积高度的增加,堰流流态在保持宽顶堰原有的流态形状的同时,堰顶整体降水趋势逐渐变缓。即堰前淤积减小了堰坎的壅水作用,使过堰水流更加平顺。
2)通过对各工况下堰流沿程水面线的分析可知,淤积高度主要影响堰前及堰上区域,在该位置处水面线随着淤积高度的增加略微下降。故实际工程中存在淤积情况下溢洪道边墙仍然满足安全超高要求。
3)淤积高度的改变会影响堰流的流速变化,且影响范围主要集中在宽顶堰的上游区域。随着淤积高度的增加,上游过水断面面积减小,断面流速整体增大。通过比较弗劳德数得出,淤积高度的增加使堰前水流由缓流逐渐向急流过渡。即宽顶堰的挡水作用被减弱,水流对坝地土体的侵蚀程度增强,不利于发挥淤地坝的拦沙减蚀效益。
4)淤积高度的改变对同一流量工况下的堰流流量系数影响较大。具体表现为,随着淤积高度的增加,流量系数逐渐增大,即宽顶堰的泄流能力有所增强。利用试验数据拟合得出了存在泥沙淤积时的宽顶堰流量系数经验公式,计算流量与实测流量平均相对误差为2.7%,可以为相关工程的流量系数取值提供参考。

