不同边界条件下热电发电器件瞬态响应特性分析

罗丁，吴海峰，杨学林

(三峡大学 电气与新能源学院，湖北 宜昌 443000)

热电发电器件作为固态能源转换元件，能够将热能直接转换为电能，具有无运动部件、无噪声和无污染等优点，是最具前景的能源转换技术之一[1-2]，已被广泛应用于航天器电源[3]、余热回收[4-6]、可穿戴设备电源[7]、太阳辐射热电发电[8-9]和火炉发电[10]等领域.为了准确分析热电发电器件在不同应用场景的输出，研究人员提出众多理论模型，包括热阻模型[11-12]和热-电耦合数值模型[13-14].Fan等[15]基于能量守恒建立热电发电器件的热阻模型，详细分析温度边界条件和对流换热边界条件对热电发电器件最大输出功率和转换效率的影响.Meng等[16]利用热-电耦合数值模型分析热电材料的变物性参数和热损失对热电发电器件输出性能的影响，并将仿真结果与热阻模型的计算结果进行对比；结果表明，热-电耦合数值模型比热阻模型更加准确.Liao等[17]利用热-电耦合数值模型对热电发电器件的输出性能进行详尽模拟，并设计试验台架对模型结果进行验证；结果表明，热-电耦合数值模型预测的输出性能与试验测量值的一致性良好.

在针对热电发电器件的理论建模与性能分析研究中，所用热源边界条件主要为稳态；在实际应用中，热源呈现非稳态特性，如太阳热辐射随天气变化和发动机尾气余热随车速变化.传统的稳态模型无法研究热电发电器件在瞬态热源下的输出响应特性，研究实际应用条件下热电发电器件的输出性能，须将传统的理论模型从稳态拓展至瞬态.鉴于热-电耦合数值模型比分析模型更加精确，Luo等[18]提出热电发电器件的三维瞬态热-电耦合数值模型，并研究热电发电器件在不同瞬态温度变化下的动态响应特性；结果表明，周期性热源能够提升热电发电器件的输出功率.Zhang等[19]建立可穿戴热电发电器件的瞬态热-电耦合数值模型，并研究在人体热能变化下器件的动态输出响应；研究结果为可穿戴热电发电器件的设计提供了理论指导.

一方面，当前关于热电发电器件的瞬态研究较少，缺乏系统性的热电瞬态响应特性分析；另一方面，现有瞬态性能研究主要采用瞬态温度变化作为边界条件，然而温度变化是连续的，使用瞬态温度边界条件存在较大误差.为此，本研究建立全面的热电发电器件三维瞬态热-电耦合数值模型，详细对比分析在瞬态温度变化和瞬态热流变化边界条件下热电发电器件的瞬态响应特性.

1 热电发电器件瞬态建模

1.1 基本结构及控制方程

选用湖北赛格瑞公司生产的TEG1-12708型热电发电器件为研究对象.该器件的P型半导体采用BixSb2-xTe3材料通过区熔生长法制备而成，N型半导体采用Bi2TexSe3-x材料通过热压烧结法制备而成.如图1所示为热电发电器件的基本结构，包含127对P型半导体和N型半导体、256个铜电极和2个陶瓷基板.为了研究热电发电器件的负载响应特性，在器件的正、负极之间添加负载电阻几何构型，并通过改变负载电阻几何构型的电阻率调节负载电阻的阻值.P型和N型半导体通过铜电极相互串联，夹于上、下端陶瓷基板之间，整体呈现电串联、热并联结构.热电半导体、铜电极和陶瓷板的尺寸(长×宽×高)分别为1.4 mm×1.4 mm×1.6 mm、1.4 mm×3.8 mm×0.4 mm、40.0 mm×40.0 mm×0.7 mm.P型和N型半导体的基本热电参数如表1所示，其中T为绝对温度，σ为电导率.

表1 TEG1-12708热电材料参数Tab.1 Thermoelectric material properties of TEG1-12708

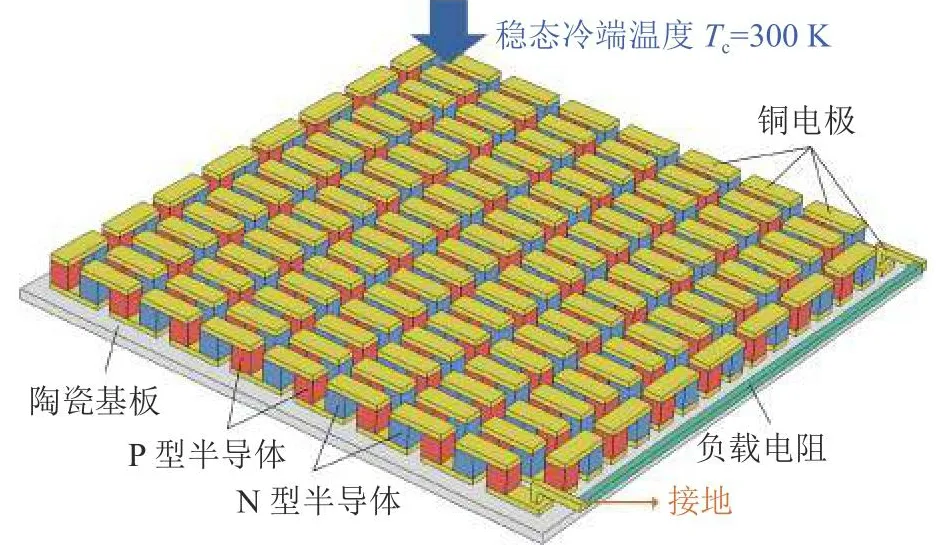
图1 热电发电器件结构示意图Fig.1 Schematic of structure for thermoelectric generator device

热电发电器件在工作过程中遵循基本的物理效应，如能量守恒、塞贝克效应、珀尔帖效应、汤姆逊效应、焦耳效应和傅里叶效应，涉及热场和电场的耦合.在热场的作用下，由于塞贝克效应，载流子的定向移动会产生电场；在电场的作用下，由于焦耳效应、珀尔帖效应和汤姆逊效应，除自身的傅里叶热传导外，还会产生额外的焦耳热、珀尔帖热和汤姆逊热，反作用于热场.这种热场和电场的相互耦合可通过下述输运方程进行描述.P型和N型热电半导体的热场能量守恒满足：

式中：ρ为材料密度，t为时间变量，J为电流密度矢量.方程左边的项表示瞬态项，方程右边的项分别表示傅里叶热传导、焦耳热、节点处的珀尔帖热和热电半导体内部的汤姆逊热.铜电极热场的能量守恒方程为

由于铜的塞贝克系数忽略不计，相比热电半导体的能量守恒方程，式(3)缺少关于珀尔帖热和汤姆逊热的方程项.陶瓷板的能量守恒方程仅存在傅里叶热传导项，即：

热电半导体的电场密度矢量表示为

式中：φ为电势，S(T)∇T为塞贝克电势.电流密度矢量J与电场密度矢量E存在如下关系：

当电流流经热电半导体、铜电极以及负载电阻时，电流满足连续方程：

式(1)～(7)构成温差发电模块热电耦合的基本输运方程，通过求解方程组即可得到模块在特定条件下的物理场分布特性.本研究借助于商业有限元软件COMSOL对上述方程进行求解.

1.2 边界条件

热电发电器件的边界条件包括热场边界条件和电场边界条件.热场边界条件包括：1)第一类边界条件，即温度边界条件，如在器件的热端表面和冷端表面分别施加热源温度Th、冷源温度Tc；2)第二类边界条件，即热流边界条件，如在模块的热端表面和冷端表面分别施加热流量Φh、Φc.热电发电器件常用于高温尾气和废水等余热回收领域，在实际应用中通过集热器从热源中汲取热量，与第三类边界条件(即热对流边界条件)不符.因此，本研究仅采用第一类和第二类边界条件.为了分析热电发电器件在不同瞬态热源下的动态响应特性，将热场边界条件定义为瞬态，并选取阶跃上升、阶跃下降、线性上升、线性下降、正弦波和三角波6种波形作为热源输入，如图2所示.在瞬态热源中，瞬态温度Th(t)的变化范围为400～500 K，瞬态热流Φh(t)的变化范围为62～128 W.理论上，温度变化是连续的，无法呈现阶跃变化，而热流可以根据能量输入的不同随意变化，因此采用瞬态热流边界条件分析热电发电器件的动态性能更为合理.将热电发电器件的冷端温度定义为稳态，采取温度边界条件为Tc=300K；在与外界环境接触的壁面上设置绝热边界条件.

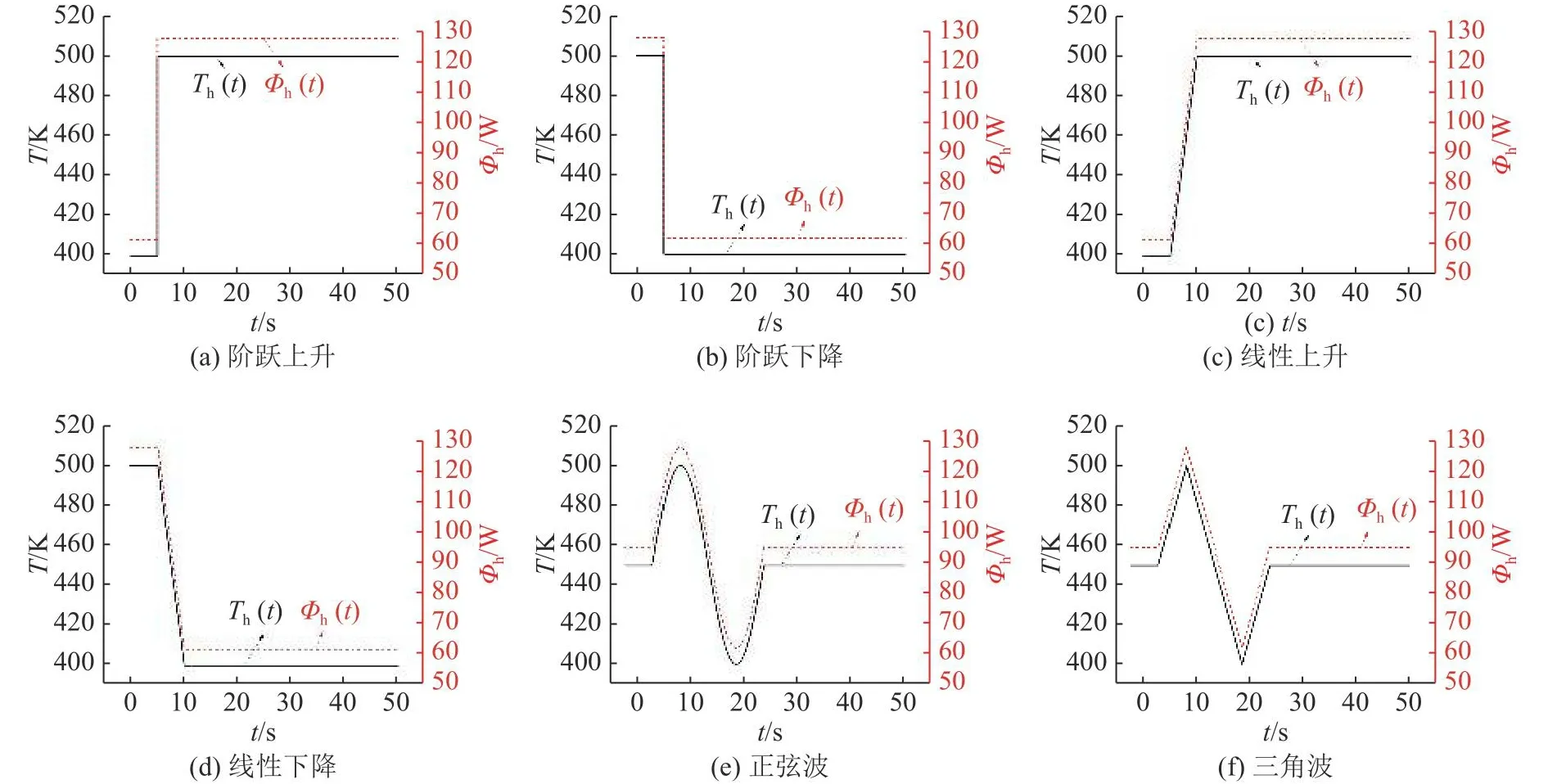
图2 瞬态热源边界条件Fig.2 Transient heat source boundary conditions

电场边界条件包括阻抗匹配边界条件和接地边界条件，即通过在热电发电器件的正、负极之间添加负载电阻研究其阻抗匹配特性，并将负载电阻与热电发电器件负极相接触的壁面定义为接地.在进行瞬态分析之前，须确定负载电阻的最优值.如图3所示，通过定义不同数值的稳态温度输入，得到热电发电器件的负载输出曲线.可以看出，无论热源温度如何变化，当负载电阻RL=2Ω时，输出功率最大，因此在瞬态性能分析中，将负载电阻固定为2 Ω.

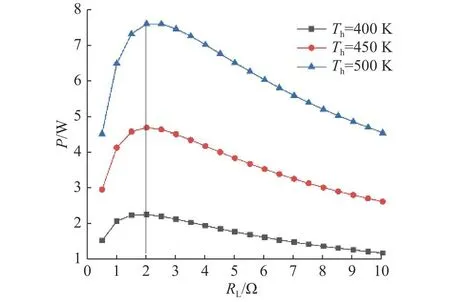
图3 热电发电器件在不同稳态温度输入下的负载输出曲线Fig.3 Load output curves of thermoelectric generator device under different steady-state temperature inputs

1.3 参数定义

热电发电器件的输出性能主要依据输出功率和转换效率进行评价，其中输出功率

式中：UL(t)为热电发电器件瞬态输出电压.转换效率

式中：Φh(t)为热电发电器件热端瞬态热流量.在稳态分析中，满足

式中：α、I和Rin分别为热电发电器件的塞贝克系数、输出电流和内阻，K、Thleg和Tcleg分别为热电半导体的导热系数、热端温度和冷端温度.等式右边的第一项至第三项分别表示珀尔帖热、热传导和焦耳热.在瞬态热流边界条件中，Φh(t)等于边界热源输入，与式(10)计算得到的值存在差异.为此，将依据式(10)计算得到的值定义为有效瞬态热流量Φh_eff(t)，对应的效率记为有效转换效率ηeff(t).另外，在数值仿真前，须分析网格独立性.为此，分别选用4种网格系统：网格I、网格II、网格III和网格IV进行网格独立性分析，其对应的网格尺寸和网格数量分别为0.2、0.4、0.6、0.8 mm，429 328、61 717、19 520、8 346.经过验证，网格I的计算时间为3 h，网格II的计算时间为20 min；网格II和网格IV的功率偏差为3.9%，网格II和网格I的功率偏差为0.3%.为了平衡计算时间和仿真精确性，选择网格II进行不同参数下模块的性能仿真.

2 结果与讨论

2.1 数值仿真结果

结合式(1)～(7)和边界条件设置，利用COMSOL仿真得到热电发电器件的输出响应特性.如图4所示为热电发电器件在正弦波瞬态热流输入下的仿真结果，选取4个特征时间点t= 5、10、15、20 s进行描述，对应的热量输入分别为95、128、95、62 W.从图4(a)可以看出，热电发电器件两端温差主要存在于热电半导体中，原因是热电半导体的热导率相对铜电极和陶瓷基板更低.t= 10 s时的热量输入最高，热端温度却低于t= 15 s时的热端温度，原因是温度变化具有热惯性，即使从t= 10 s至t= 15 s时的热量输入降低，温度仍会在t= 5 s至t= 10 s的上升趋势中维持一段时间.热电发电器件的输出电压与热端温度成正比，使得输出电压在不同时间点的变化趋势与温度变化趋势保持一致，如图4(b)所示.t= 5 、10、15、20 s时的输出电压分别为3.03、3.34、3.43、2.92 V.根据式(8)计算得到相应地输出功率分别为4.59、5.57、5.88、4.25 W.可以初步看出，依靠温度变化的热惯性，利用瞬态热源激励可以提升热电发电器件的输出性能.图4(c)为电流密度J的分布云图，由于铜电极的电阻率最低且横截面积最小，其电流密度最大；由于电流方向的不同，相邻两列铜电极的电流密度为相反数.另外，热电发电器件的电流变化趋势与电压变化趋势保持一致.

2.2 瞬态温度边界条件下的输出响应特性

如图5所示为瞬态温度边界条件下的输出功率与转换效率.从图5(a)、(b)可以看出，输出功率随着热源温度的波形变化而发生相应变化.由于热惯性的影响，在温度阶跃上升的拐角处，输出功率呈现一定尖角，在线性、三角波和正弦波的热源变化中，输出功率变化更为平缓.根据式(9)，输出功率与转换效率成正比，因此转换效率与输出功率保持一致的变化趋势，如图5(c)、(d)所示.不同的是，相比图5(b)，图5(d)中的转换效率曲线更偏向于下半周期，原因在于转换效率受输出功率和热端热流量的共同影响，而输出功率在下半周期由于热惯性的影响，维持在相对较高的区间.由于温度变化是连续的，在实际情况中，温度无法呈现规律的阶跃变化和线性变化，采用热流边界条件分析热电发电器件的瞬态响应特性更为合理.

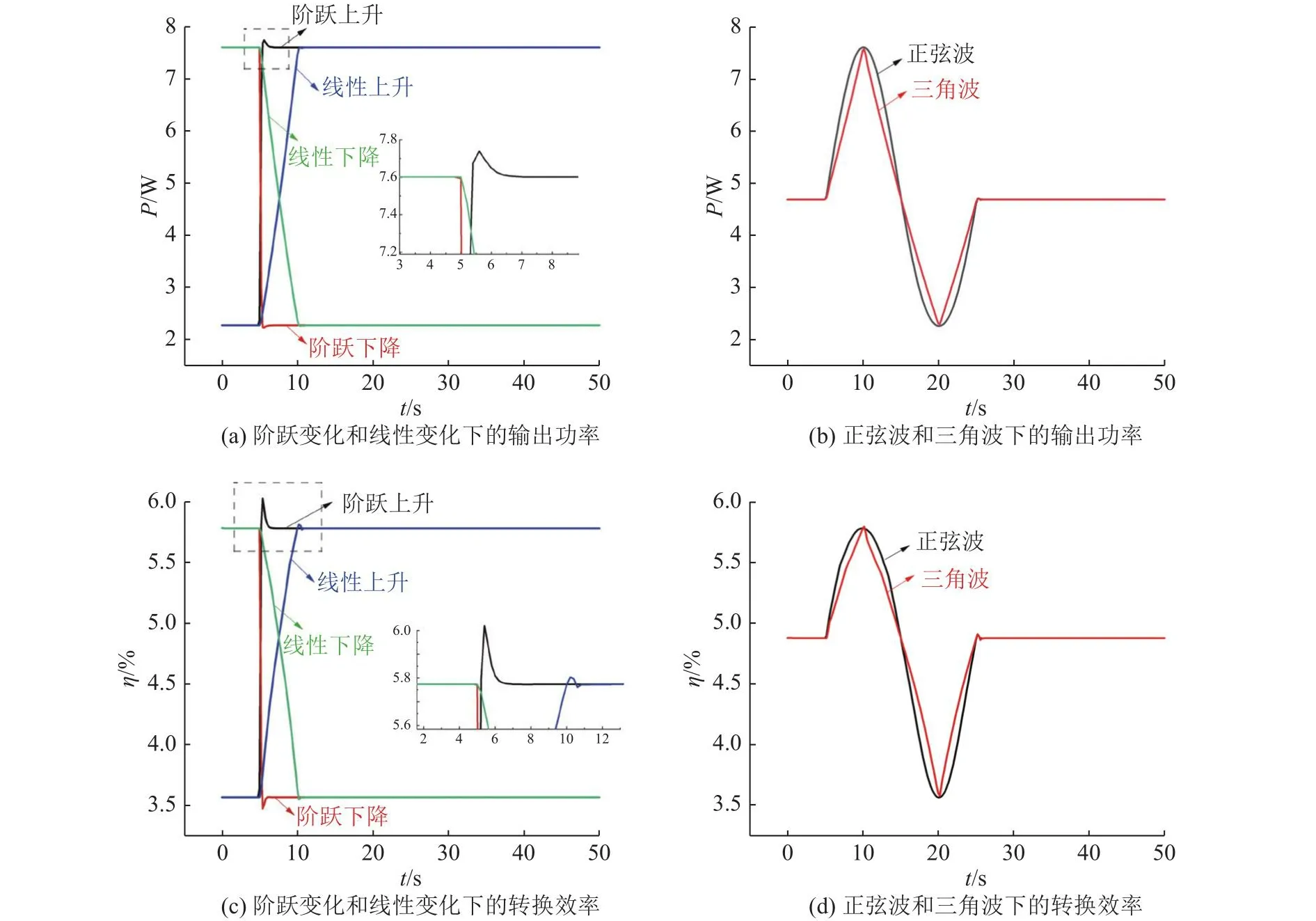
图5 瞬态温度边界条件下的输出功率与转换效率Fig.5 Output power and conversion efficiency under transient temperature boundary conditions

2.3 瞬态热流边界条件下的输出响应特性

如图6所示为瞬态热流边界条件下的输出功率.可以看出，相比瞬态温度边界条件，瞬态热流变化下的输出功率曲线更为平缓.即使热流输入阶跃变化，输出功率也缓慢变化，与线性热流输入下的输出功率呈现近似的变化趋势，且由于热惯性的影响，当t= 35 s时输出功率才达到稳态，存在明显的时滞现象.相比三角波热流输入，由于正弦波热流输入平滑变化，其输出功率的变化幅度更大.另外，在热流变化的拐角处，输出功率呈现光滑过渡的变化过程.由图2、6可以得出，热惯性对从瞬态热流输入到功率瞬时响应的过程具有一定的缓和作用.

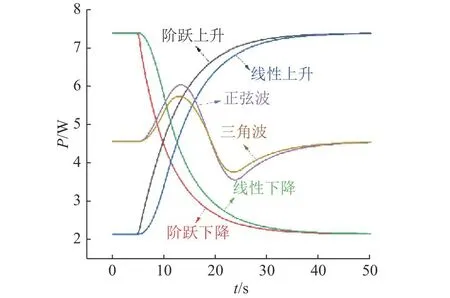
图6 瞬态热流边界条件下的输出功率Fig.6 Output power under transient heat flux boundary conditions

如图7所示为瞬态热流边界条件下的转换效率与热流量.与输出功率平缓变化不同的是，由于转换效率与热端热流量成反比，转换效率急剧变化.鉴于热流量计算公式的不同，对比分析转换效率η(t)和有效转换效率ηeff(t)，对应的热流量和有效热流量分别为Φh(t)和Φh_eff(t).由于η(t)直接根据热流输入Φh(t)进行计算，其变化趋势主要受热源曲线的影响，Φh_eff(t)通过热电半导体的珀尔帖热、热传导和焦耳热计算得到，在热惯性的缓和作用下，Φh_eff(t)表现出与输出功率一致的变化趋势.理论上，η(t)通过真实的热流量输入进行计算得到，结果更加准确，直接反应热电发电器件的瞬态响应特性，ηeff(t)根据热电半导体两端的热流量变化进行计算得到，更能反应热电半导体的瞬态热电转换能力.因此，式(10)仅适用于稳态情况下热电发电器件的转换效率计算，瞬态情况下应通过直接读取热电发电器件的热端热流量计算转换效率.

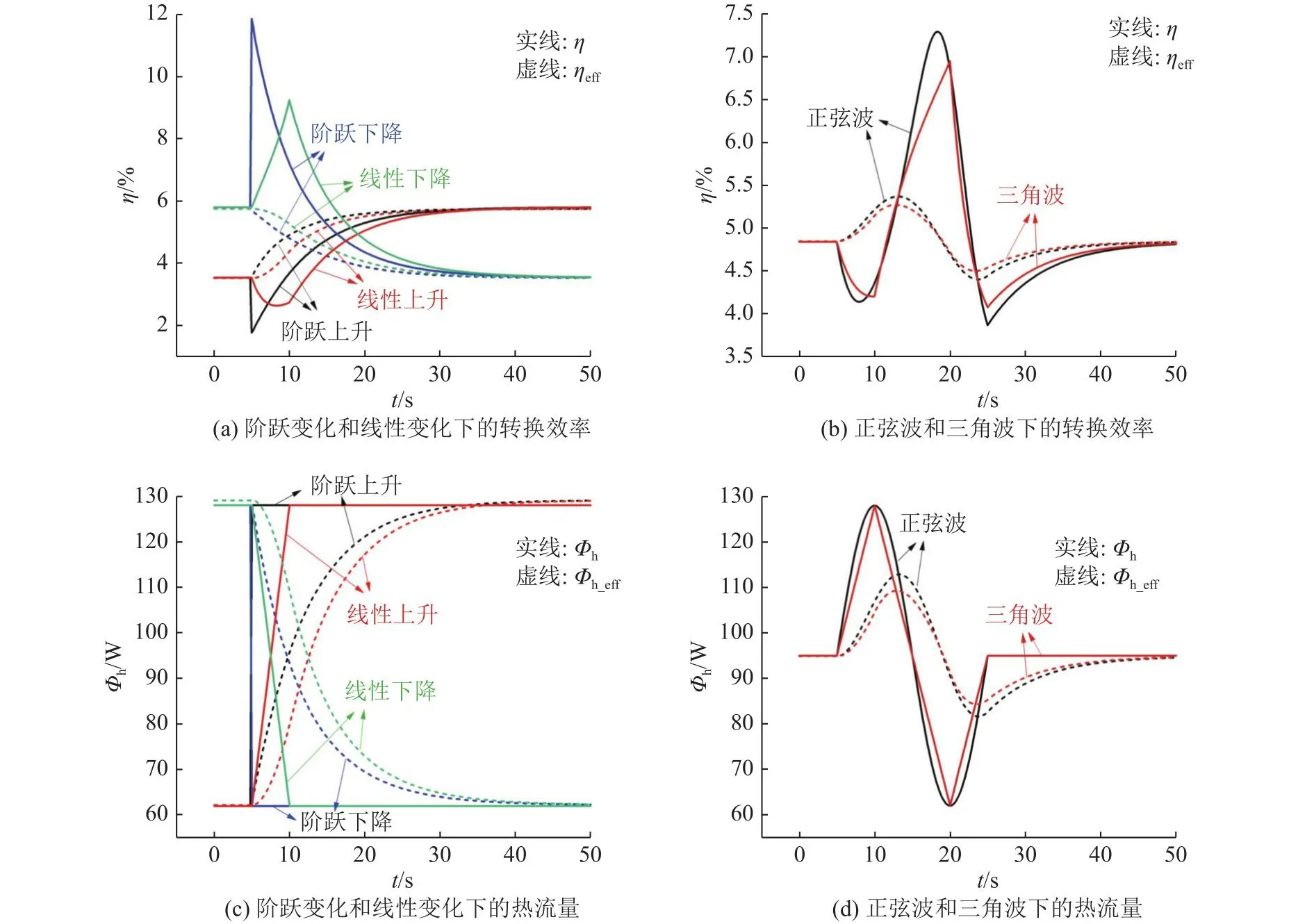
图7 瞬态热流边界条件下的转换效率与热流量Fig.7 Conversion efficiency and heat absorption under transient heat flux boundary conditions

为了进一步分析热电半导体在瞬态热流激励下的热流量变化，根据瞬态仿真结果得到傅里叶热和热端珀尔帖热的变化曲线，如图8所示，其中傅里叶热即为热传导.结合图6可以看出，在式(10)中，傅里叶热占据热端热流量的绝大部分，其次分别是热端珀尔帖热和焦耳热.在热惯性的作用下，傅里叶热、热端珀尔帖热和焦耳热三者呈现几乎一致的变化趋势，引起图7中有效转换效率ηeff(t)的相应变化.

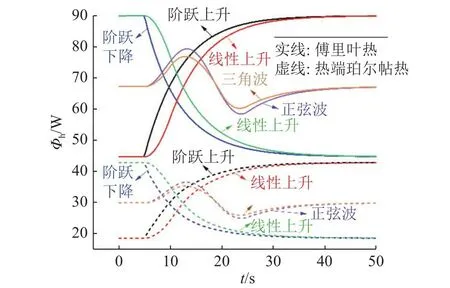
图8 瞬态热流边界条件下热电半导体的热量变化Fig.8 Heat changes of thermoelectric semiconductors under transient heat flux boundary conditions

2.4 不同边界条件下的温度对比

对比瞬态温度输入和瞬态热流输入2种边界条件下热电发电器件的瞬态响应特性，如图9所示为不同边界条件下的温度变化曲线.可以看出，瞬态温度输入的热电半导体热端温度Th_leg与热源温度Th保持一致的变化趋势，原因是导热热阻仅引起温度下降，对温度变化趋势无影响.同理，瞬态热流输入的Th_leg与Th的变化趋势也保持一致，但热源温度Th与图2中瞬态热流Φh(t)的输入曲线存在较大差异，原因在于，热电发电器件的热流量输入急剧变化，温度呈现连续变化，且具有热惯性，导致热源温度以平缓的趋势响应.

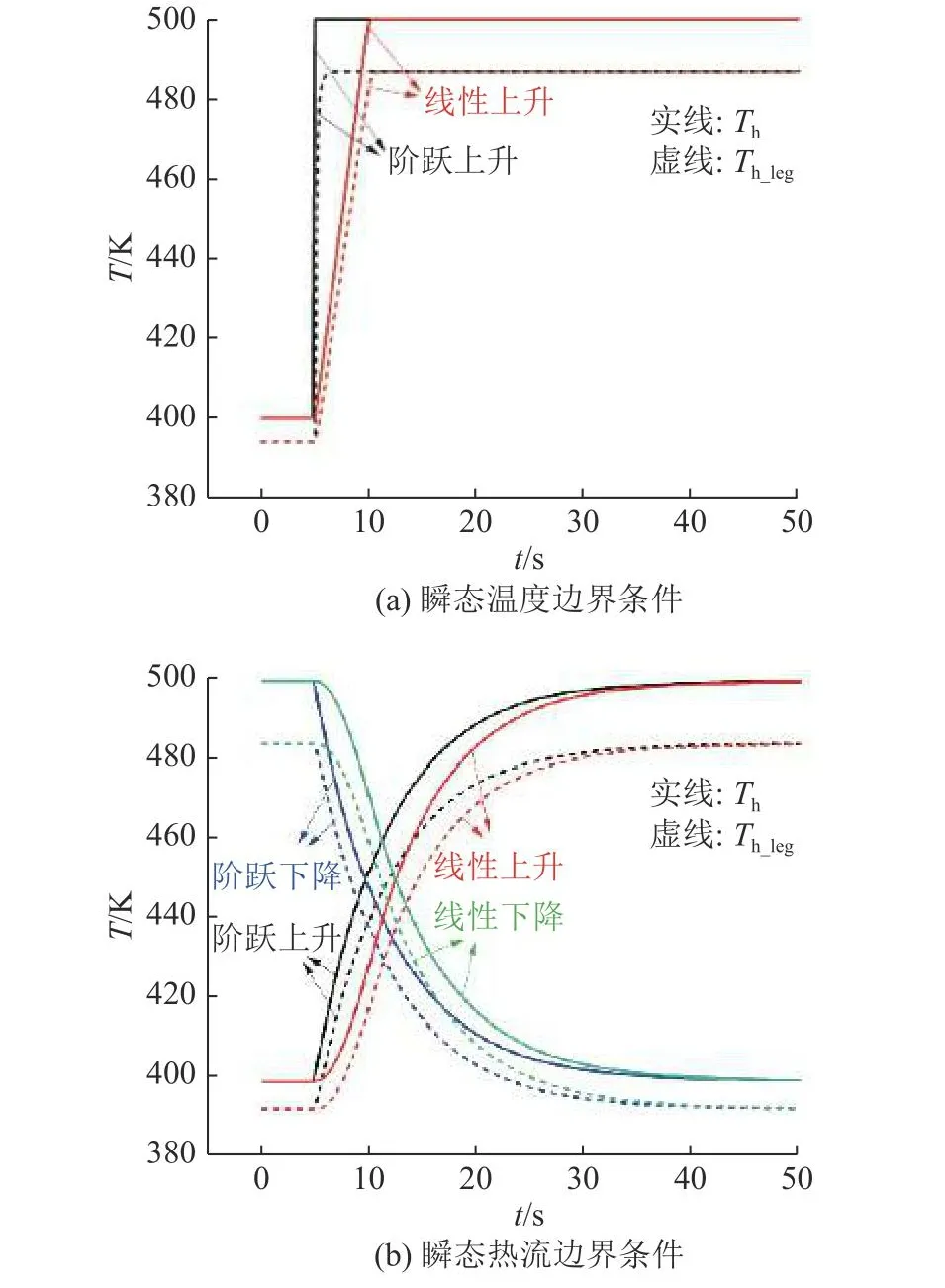
图9 不同边界条件下的温度变化Fig.9 Temperature changes under different boundary conditions

如图10所示为不同边界条件下的输出功率与转换效率变化曲线.由图10(a)可知，相较温度边界条件下输出功率的瞬时变化，热流边界条件下的输出功率变化更为平缓，结果更符合实际情况.因此，在热电发电器件的瞬态性能仿真中，应采用瞬态热流边界条件，而非瞬态温度边界条件.从图10(b)可以看出，温度边界条件下的转换效率η(t)与热流边界条件下的有效转换效率ηeff(t)和图10(a)中相应的输出功率曲线保持一致的变化趋势，原因是其热端热流量均通过计算热电半导体的珀尔帖热、傅里叶热和焦耳热得到.不同的是，热流边界条件下的转换效率η(t)由于直接通过热流量输入的大小进行计算，变化趋势与热流输入密切相关，且结果比采用温度边界条件更为准确.通过观察可以得到，正弦波热流输入下的平均转换效率或高于其稳态值.

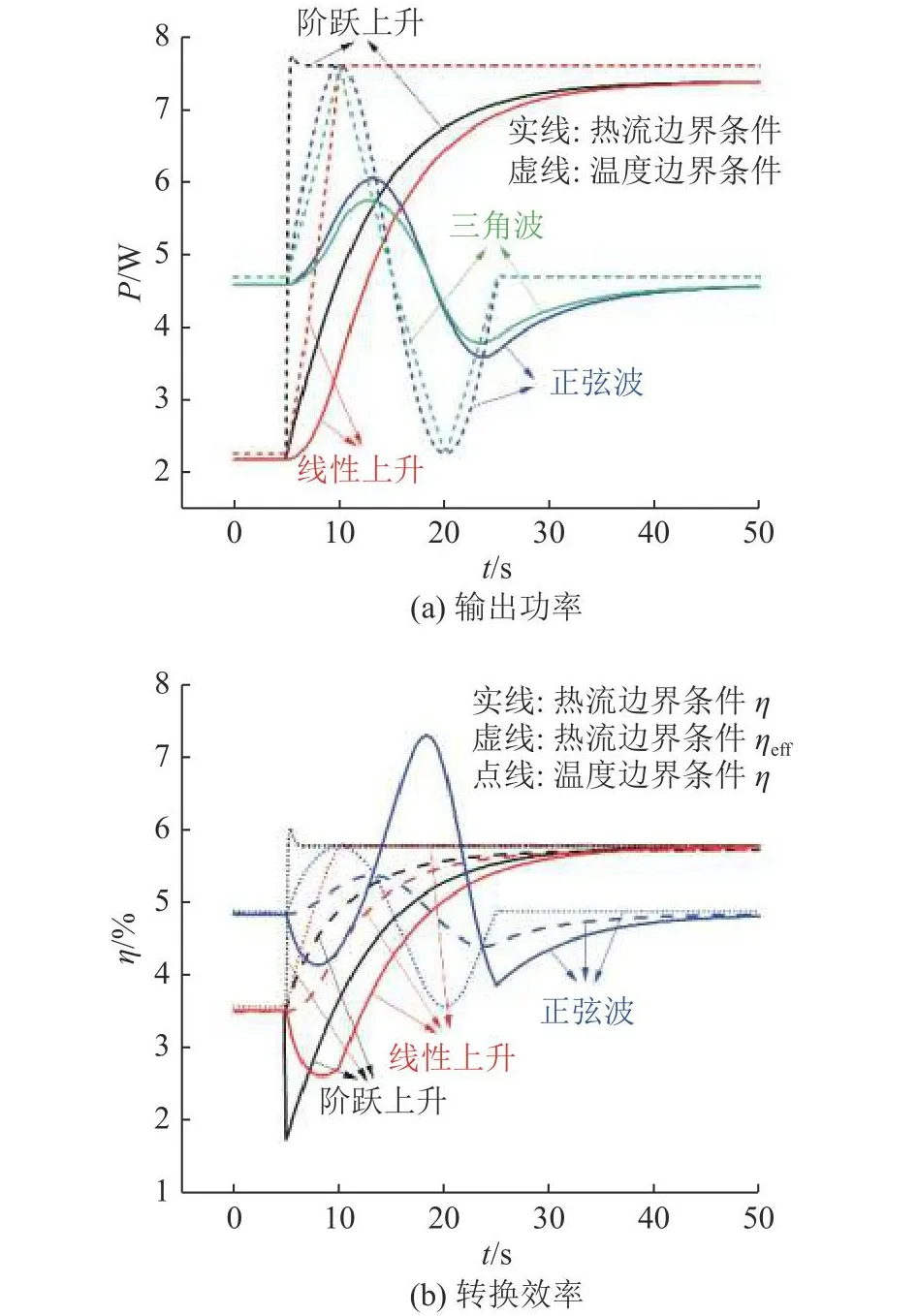
图10 不同边界条件下的输出功率与转换效率Fig.10 Ouput power and conversion efficiency under different boundary conditions

2.5 不同边界条件下的瞬态性能与稳态性能对比

热电发电器件的输出性能常采用稳态模型进行分析，但稳态模型会造成预测值的偏差[20]，瞬态模型更为准确.本研究对比稳态模型与瞬态模型仿真得到的输出性能，以进一步分析两者的偏差.如图11所示为温度边界条件和热流边界条件下瞬态性能的平均值与稳态性能的对比.从图11(a)可以看出，无论何种热源波形，稳态模型均会造成输出功率预测值偏低和转换效率预测值偏高.由于瞬态温度边界条件的局限性，瞬态热流边界条件下的稳态与瞬态性能对比更具合理性.由图11(b)可知，在阶跃上升和线性上升的热源波形中，稳态模型会造成输出功率(偏差分别为37.48%和32.14%)和转换效率(偏差分别为35.23%和31.98%)的预测值偏高，在其他热源波形时则相反.尤其在阶跃下降和线性下降的热源波形中，稳态功率和稳态转换效率明显低于瞬态功率(偏差分别为42.05%和36.25%)和瞬态转换效率(偏差分别为55.34%和41.54%)的平均值.在阶跃上升和线性上升的热源波形中，有效转换效率ηeff(t)明显高于转换效率η(t)，在阶跃下降和线性下降的热源波形中则相反.因此，若采用式(10)计算瞬态转换效率，会造成较大的误差.上升与下降这2类热源波形存在较大差异的原因主要是热源初始状态的不同.因此，对正弦波和三角波周期性热源下的瞬态性能与稳态性能进行对比，研究周期性热源对热电发电器件瞬态响应特性的影响.从图11(b)可以得出，周期性热源不仅能提升热电发电器件的输出功率，还能提升其转换效率.相比稳态输出性能，正弦波和三角波热源下的输出功率分别提升了7.48%和5.76%，转换效率分别提升了11.58%和8.48%.该结果表明，周期性热源能够有效提升热电发电器件的输出性能，并且正弦波热源的提升效果大于三角波.

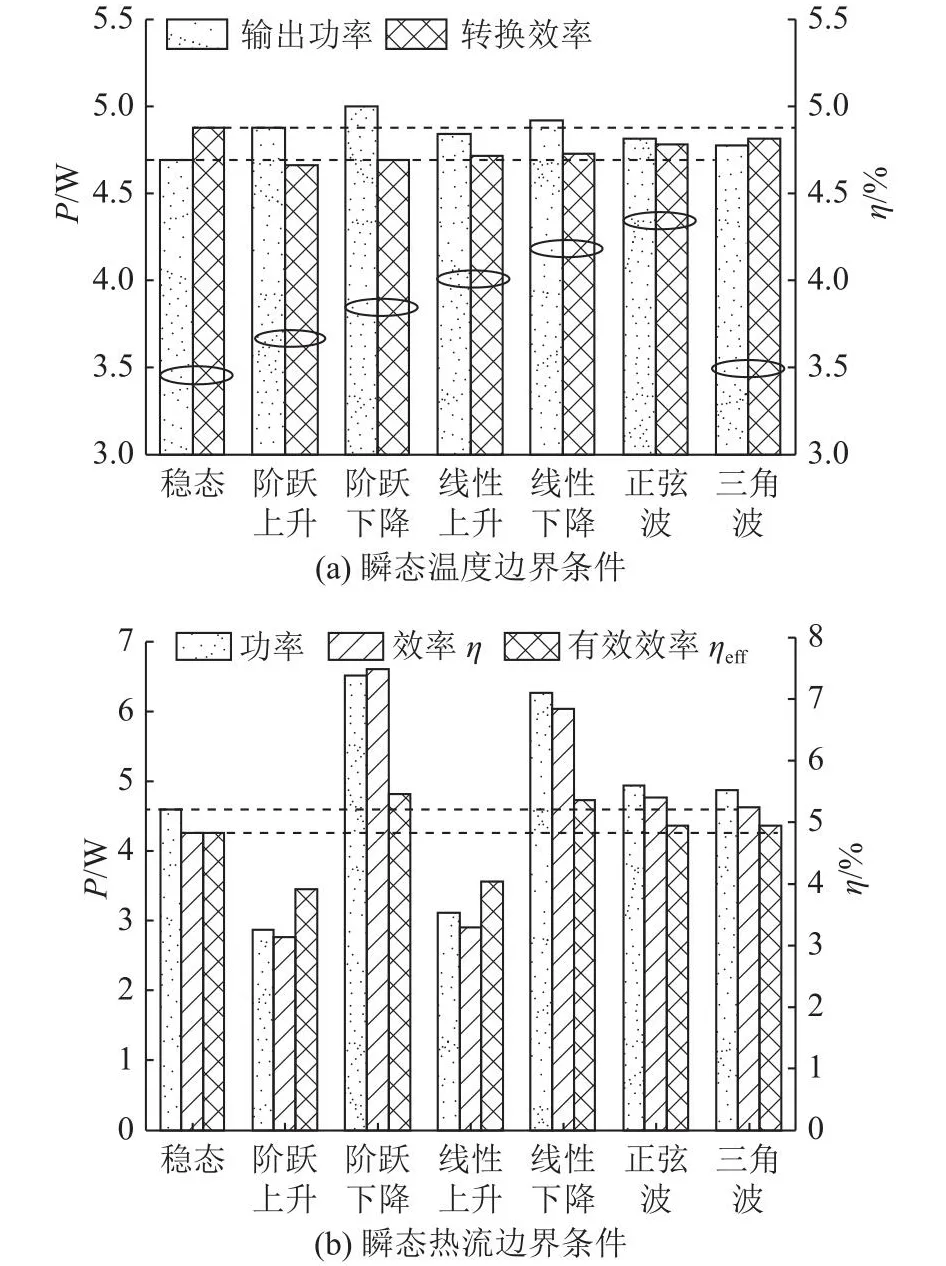
图11 不同边界条件下的瞬态性能与稳态性能对比Fig.11 Comparison of transient and steady-state performance under different boundary conditions

3 试验验证

3.1 试验台架搭建

为了验证瞬态热-电耦合数值模型的准确性，设计如图12所示的试验台架.在试验过程中，使用焦耳加热器为热电发电器件提供热源，并通过改变电源(HCP1022, Henghui, 中国)的电压波形来产生瞬态热源.在热电发电器件冷端，使用铝制水冷散热器进行散热，并通过恒温水浴(DC-0530，zhulan，中国)保持恒温.为了避免与环境空气接触引起的热损失，在焦耳加热器的底部放置隔热块，并且所有部件均采用隔热材料包裹.将温度传感器(SA1XL-K-SRTC，OMEGA，美国)附在热电发电器件的两端，以测量热端和冷端温度；利用数据采集仪(34970A，Keysight，中国)记录和存储温度数据.为了测量热电发电器件的瞬态输出性能，将电子负载(IT8500+，ITECH，中国)与热电发电器件的正负极相连以形成回路.试验台采用夹紧装置夹紧；将电源、数据采集仪和电子负载与计算机相连，进行信号控制与处理；将相应的试验条件用作瞬态数值模型的边界条件，完成瞬态性能仿真.

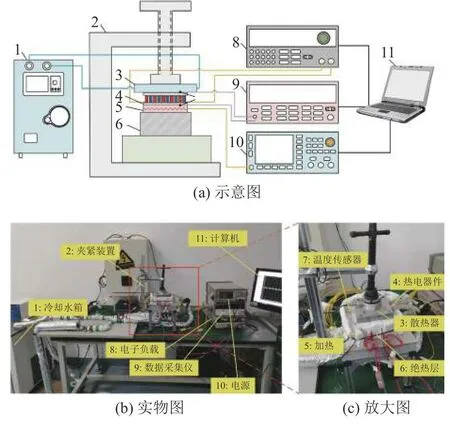
图12 瞬态试验台架Fig.12 Transient experimental test rig

3.2 仿真结果与试验结果对比

如图13(a)所示为热电发电器件的冷端温度和热端热流量，将其用作瞬态数值模型的边界条件.在数值仿真中，将隔热块等效为80 W/(m2·K)的换热边界条件，使仿真条件与试验条件保持一致.如图13(b)所示为试验结果和模型结果之间瞬态输出电压和输出功率的对比.可以观察到，瞬态电压和瞬态功率的试验结果与仿真结果具有相同的变化趋势，仿真结果的波动幅度更大.原因是焦耳加热器的加热过程是连续且缓慢的，而仿真未考虑焦耳加热器的加热过程.输出电压和输出功率的平均误差分别为3.30%和6.58%，该误差对于瞬态试验而言是可接受的，进一步表明瞬态热-电耦合数值模型的准确性.

图13 仿真结果与试验结果对比Fig.13 Comparison between simulation and experimental results

4 结 论

本研究提出瞬态热-电耦合数值模型，分析热电发电器件在阶跃上升、阶跃下降、线性上升、线性下降、正弦波和三角波6种热源波形下的瞬态响应特性.考虑到热源边界条件的不同，对瞬态温度和瞬态热流2种瞬态边界条件下的输出性能进行详细的对比分析，得到如下结论.

（1）三维瞬态热-电耦合数值模型能够准确模拟热电发电器件在实际非稳态工况下的瞬态响应，得到热电发电器件在不同时间点的物理场分布特性.试验结果表明，该模型的输出电压和输出功率的平均误差分别为3.30%和6.58%.

（2）由于温度变化具有连续性和热惯性，热源温度无法实现阶跃上升和阶跃下降变化曲线，瞬态热流直接受输入热能的影响，可以任意变化.建议采用瞬态热流边界条件分析热电发电器件的瞬态响应特性.

（3）受热惯性的影响，即使热源输入急剧变化，热电发电器件的输出功率呈现平缓的变化趋势，且存在时滞现象.转换效率受热源输入的影响而急剧变化，且应直接由热流输入计算其转换效率，若根据热电半导体的热量变化进行计算，将导致较大误差.

（4）在阶跃下降的热源波形中，稳态模型预测的输出功率和转换效率比瞬态模型的预测值分别低了42.05%和55.34%.在正弦波和三角波的周期性热源中，热电发电器件的输出功率分别提升了7.48%和5.76%，转换效率分别提升了11.58%和8.48%.

在实际应用中，热电发电器件常用于流体余热回收，热源并非直接施加在器件的热端表面上，今后研究中将进一步分析流体余热变化下的热电器件瞬态性能.