单波长激光通信终端的隔离度

高伟饶，董科研*，江 伦

（1.长春理工大学 光电工程学院, 吉林 长春 130022；2.长春理工大学 空间光电技术研究所, 吉林 长春 130022）

1 引 言

空间激光通信具有通信频带宽、数据传输速度快、良好的性价比、易于部署和通信安全等优点，系统整体体积小、重量轻、功耗低，在很多领域均有需求[1-3]。因此，一对一、一对多的空间激光通信得到了高速发展[4-6]。目前，空间激光通信多采用收发一体式的双工通信，即信号的接收和发射使用共同的光学天线。这种方法既节省了空间又提高了通信效率[7]。但在通信发射阶段整体光学系统内的光机等器件会产生后向散射光，杂散光会通过光路返回并进入探测器，从而造成信噪比降低，甚至直接吞灭接收到的信号，严重影响通信质量。

吕博[8]等人针对同轴两反射镜在未使用主镜筒外遮光罩的前提下，对次镜遮光罩进行优化设计以实现杂散光抑制。验证了紧凑型大视场折反射光学杂散光抑制结构的可行性。夏方圆[9]等人通过对卡塞格伦光学天线的次镜打孔和在光路中增加光陷阱的方式抑制后向散射，提高系统隔离度。曲杨[10]等人在3D 激光视觉系统中，利用偏振分光隔离的方法，以及通过旋转一定角度来降低λ/4 波片表面反射杂散光，上述方法均达到了较好的隔离效果。然而，目前针对激光通信系统中光学单元的加工工艺与光学设计结构相结合的研究相对较少，因此有必要通过激光通信系统中光学单元的加工工艺要求与光学设计结构对共口径通信结构的隔离效果进行详细分析。

本文设计了一个由抛物面反射镜和透镜组成的离轴抛物面反射式光学结构，对结构中透镜元件的表面粗糙度和透镜元件表面清洁度两方面展开研究，并对激光通信终端进行仿真分析。最后得出以下结论：终端内关键元件表面粗糙度会影响隔离性能，隔离度随粗糙度的增大逐渐变小。同时，在同等条件下，随着各个元件表面清洁度水平的提高，激光通信终端内隔离性能也会逐渐降低。

2 整体结构设计

为满足激光通信系统的设备要求，本文设计了一种收发一体的双工通信模式，如图1 所示。本方案中使用56°偏振分光棱镜进行偏振分光。常用的45°偏振分光棱镜以45°角入射，反射光与入射光成90°角，本方案与其不同。本方案中，光束以布儒斯特角入射，反射光与折射光互相垂直。这样可以相对减少由棱镜透射的部分偏振光在通道壁反射后的回光对信号接收端的影响。

图1 激光通信整体结构Fig.1 Structure of the laser communication system

同时，由图1 可以看出整体的工作情况如下：信号光通过λ/2 波片调整偏振方向，S 线偏振光经56°偏振分光棱镜反射到λ/2 波片、λ/4 波片，偏振态转换为圆偏振光，由光学天线发射信号。信号接收时，光学天线接收到圆偏振光后，经过λ/2 波片、λ/4 波片转换为P 线偏振光，最后由56°偏振分光棱镜和检偏器同时对P 线偏振光以外的杂散光进行隔离，并由信号接收机对信号进行接收分析。但在信号传输过程中，其他光学元件和天线结构所产生的表面散射仍然会以杂散光的形式到达信号接收端，导致信噪比下降。所以需要分析光学天线和整体结构中的影响因素，提高系统通道内的隔离度。

3 杂散光分析理论基础

3.1 隔离度模型定义

本文主要研究信号光在传输过程中对信号接收端的影响。根据信号光收发通道隔离的定义，隔离度可以写为[11]：

其中：Ei表示信号光的发射功率，Er表示信号接收端的杂散光功率。

设发射信号光S 线偏振光琼斯矢量为：

信号光在系统中传输的过程中，信号接收端接收到的光学系统中的后向辐射杂散光功率可表述为[11]：

式中：Ir表示信号接收端接收到的杂光光强， Ω表示信号接收的立体角，FBRDF表示光学系统中光学元件表面的双向反射函数。

使用Kirchhof 理论对双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)建模，表示元件表面反射及散射情况[12]。则粗糙元件表面反射光可以表示为：

Fsp一般包括镜面反射，Fdd表示漫反射或者说是镜面反射和漫反射之间的反射，Fud表示均匀漫反射。通常，镜面反射是部分偏振的，并且相对于照明区域的局部表面法线指向镜面方向。但是当镜面反射的一部分光入射到材料表面的另一部分上时，则会产生镜面反射偏振的部分偏振，并且再次指向相对于该照明区域的局部表面法线的镜面方向。重复多次会导致散射，该散射是非偏振的。所以本文只考虑Fud均匀漫反射产生的偏振相关杂光对信号接收端的影响。公式(4)可写为：

总积分反射(Total Integrated Scatter, TIS)[13]作为元件材料表面的一个重要光学特性，可以表达元件表面的均方粗糙度。其与粗糙度之间的关系可表示为：

其中： σ为镜面均方粗糙度；λ表示波长； θi为反射角； ∆n为 元 件 界 面 折 射 率 差( ∆n=2 为 反 射 镜面)。基于Lambert 散射模型的定义，光学系统中各元件表面上的双向反射率分布函数(FBRDF)与TIS 之间的关系可以写成：

波信号接收立体角 Ω可以通过接收端光学孔径D和光学子系统后截距L1表述：

根据图1 所示路径可知，信号光到达光学天线抛物面的光强可以表示为：

其中：J3、J2、J1表示反射镜琼斯矩阵；Jhwp、Jqwp、Jpbs分别表示二分之一波片、四分之一波片、偏振分光棱镜的琼斯矩阵；r1、r2、r3、r4表示反射系数。

通过穆勒矩阵对后向反射光推导到达探测器的光强，则经归一化的自然光斯托克斯矢量为：

其中：rb表示能量分光镜的反射系数；检偏器、偏振分光棱镜、四分之一波片、二分之一波片的穆勒矩阵分别为Mp、Mpbs、Mqwp、Mhwp；反射镜的反射系数分别r1、r2、r3、r4。所以后向反射杂光到达信号接收端的杂光光强为：

将公式(12)代入公式(3)后与公式(1)联立得到激光通信终端信号发收隔离度公式为：

鉴于各个光学元件的反射系数、消光比以及接收立体角均为已知的固定数值，并且波片的旋转角度对隔离度影响较小，所以本文使用TracePro 软件对光路中的光学元件表面粗糙度进行隔离度仿真分析。同时，通过光学元件的表面清洁度对隔离度的大小进行仿真分析。

3.2 基础理论模型

本文针对光学望远单元中离轴抛物面、离轴反射镜、准直透镜组和系统中λ/2 波片、λ/4 波片的表面粗糙度和表面清洁度进行仿真分析。通过Harvey 模型与ABg 模型对望远单元和通信支路中的各个元件进行BRDF 建模，并通过TracePro 软件模拟隔离度的变化。

3.2.1 表面粗糙度模型

双向散射分布函数(Bidirectional Scattering Distribution Function, BSDF)表示结构中各个单元的散射特性[14-15]。本文在杂散光分析中主要考虑光学单元的反射特性，所以使用BRDF 代替BSDF。杂散光的强弱与BRDF 有直接关系。降低BRDF，可以降低信号通道内的杂光传输。所以本文主要建立BRDF 模型。

Harvey 模型是对光学表面BRDF 进行建模的常见方法，并得到了大多数杂散光软件的支持。ABg 模型与Harvey 模型非常相似，可以利用Harvey 模型对ABg 模型参数进行计算仿真。ABg 模型是直接应用TracePro 软件的一种模型计算方式，其函数形式为：

其中： θs、θi分别为散射角和镜面反射角，是常数，L2的翻转角，通常在0.001 量级或者更小量级，s 表示Harvey 模型取值大于L2时的斜率因子，用于表示镜面散射分布程度。获得数据拟合时，Harvey 模型中的常数可以通过TIS 计算得到[16]：

当取得典型值，波长为测试波长（632.8 nm）时，Harvey 模型与ABg 模型可以通过相应的公式得出与其对应的ABg 模型参数，如图2（彩图见期刊电子版）所示。公式如下[17]：

图2 Harvey 模型与ABg 模型Fig.2 Harvey and ABg models

本文中，系统工作波段为1 550 nm，对于系统光路中λ/2 波片、λ/4 波片及准直透镜组，选取表面粗糙度分别为3、6、9、12、15 nm，分析隔离度的变化。

不同均方粗糙度下的ABg 散射模型参数见表1。

表1 不同表面粗糙度ABg 模型参数Tab.1 ABg model parameters for different surface roughnesses

已知光轴的入射角，通过公式(6)计算得到光学天线中离轴抛物面与离轴反射镜的表面粗糙度分别为3、6、9、12、15 nm 时的TIS 数值。根据Harvey 模型计算不同均方粗糙度相对应的ABg模型参数，如表2 所示。

表2 不同表面粗糙度光学天线ABg 模型参数Tab.2 ABg model parameters of the optical antenna with different surface roughnesses

3.2.2 表面污染模型

洁净元件表面的颗粒污染水平通常通过表面清洁度(Contamination Level, CL)[18]描述，通常使用针对洁净室规范导出的(IEST)CC1246D标准定义分布。给出了清洁度或“污染水平”的函数：

其中：CL 表示表面的清洁度水平；N表示直径大于或等于微米的每平方英尺的颗粒数量。斜率常数在文中取0.926，表示在洁净元件表面进行颗粒污染分析。图3（彩图见期刊电子版）给出了不同CL 下，N与 β1之间的关系。

图3 CL 分别为200、400、600、800 时对应的N 与β1 之间关系Fig.3 The relationship between N and β1 when CL are 200, 400, 600 and 800, respectively

对颗粒分布进行分析，将所有不同大小的污染颗粒的污染颗粒密度之和定义为污染颗粒覆盖率 (Percent Area Covered, PAC)[16]。颗粒覆盖面积百分比PAC 计算如下：

式中M为常数，当 α=0.926，M=-7.245时，表面污染散射引起的表面总积分散射(TIS)可通过污染颗粒覆盖率(PAC)得到：

依据颗粒覆盖率和表面清洁度的关系，以及颗粒覆盖率和BRDF 的比例关系，在1 550 nm 工作波长表面清洁度分别为200、400、600、800 时对应的污染颗粒覆盖率分别为4.55×10-3、0.106、0.798、3.63。通过公式(22)可得到不同清洁度(CL)水平下的颗粒污染BRDF 数据，并将其数值用ABg 模型进行拟合，如表3 所示。

表3 不同清洁度(CL)ABg 模型参数Tab.3 ABg model parameters for different contamination levels

4 测量实验与结果

4.1 整体光学设计

光学天线采用离轴抛物面式设计，以提高通信收发及探测视场，而无中心遮拦的设计则降低了系统能量损耗。如表4 所示：表中的指标参数为设计要求，中心波长采用1 550 nm；系统的缩束倍率为10 倍；出射口径为Ф75 mm；系统的最后接收视场按照信标探测的视场进行设计；设计视场为5 mrad。

表4 光学设计指标Tab.4 Optical design indexes

根据表4 中的指标利用Zemax 软件完成了如图4 所示的光学设计。

图4 光学设计整体布局图Fig.4 Overall layout diagram of optical design

光学系统的MTF 曲线如图5(彩图见期刊电子版)所示。由图5 可知，调制传递函数曲线在0°视场时接近衍射极限。该光学设计中，主镜为离轴抛物面，其他的转折镜均为平面反射镜，这样可以最大限度地节省空间，实现设备的小型化。

图5 光学系统的MTF 曲线Fig.5 MTF of the designed optical system

对所设计光路建立整体的光机结构，如图6 所示。通过平面反射镜转折光路将整个系统放置在一个平板的左右两侧，充分利用了整体空间。图6(a)为光学天线的缩束系统，图6(b)为光学系统的子光路，信号的发射端、接收端、56°偏振分光棱镜、λ/2 波片、λ/4 波片等元件。且在使用TracePro 软件进行分析时，端机的材料设置为铝材料，并进行涂黑漆处理，透镜元件按照设计提供的材料和计算出的模型参数进行设置。

图6 光学机械结构Fig.6 Optical-mechanical structures

4.2 系统中镜面粗糙度对端机隔离度的影响

在TracePro 中设置表1，表2 中换算得到的ABg 模型参数，改变λ/2 波片、λ/4 波片及光学天线表面的ABg 模型参数，分析不同粗糙度对隔离度的影响，同时，确定表面清洁度水平为CL=400，本文设置为洁净元件表面进行颗粒污染分析，且CL=500 以下的颗粒污染的BRDF 要远小于洁净镜面的BRDF，其对颗粒污染镜面BRDF 的贡献相对减少[15]。在1 550 nm 工作波长下，表面清洁度在400 时对应的污染颗粒覆盖率为0.106，相应参数如表3 所示。探测器接收端接收的回光仿真结果如图7 所示。TracePro 中设置发射总光线数为70 万，总光通量为1 W，光线追迹阈值为1×10-7。

图7 不同表面粗糙度下的端机接收面光通量。（a）3 nm；（b）6 nm；（c）9 nm；（d）12 nm；（e）15 nmFig.7 The luminous flux of the receiving surfaces under different surface roughnesses.(a) 3 nm; (b) 6 nm; (c) 9 nm;(d) 12 nm; (e) 15 nm

通过图中光通量可计算出在不同粗糙度情况下激光通信终端内部的隔离度，如折线图8 所示。由图8 可知，在各个元件参数相同的情况下，改变λ/2 波片、λ/4波片及光学天线镜面粗糙度参数，相比于3 nm 镜面粗糙度，当镜面表面粗糙度为15 nm 时，隔离度降低了13.28 dB。同时，使用Matlab 软件绘制公式(13)隔离度曲线图。式中反射系数设置为0.99，偏振分光棱镜的消光比设置为0.001， θi设置为0.02 rad，最终与表面粗糙度相关的隔离度曲线如图9 所示。通过对比两折线图可以发现表面粗糙度在3 nm 至15 nm 区间变化时其隔离度的降低趋势基本一致。两种计算方式中，Matlab 软件是利用文中公式(13)模型进行的隔离度计算，公式中的反射系数、琼斯矩阵等模型考虑了根据Zemax 设计计算光学元件带来的影响，所以其计算过程不考虑激光通信终端内其他机械器件散射情况，结果更趋近于理想情况。Tracepro 软件是依据设计的整体激光通信终端模型进行仿真，仿真中对于机械结构组件会设置材料属性，光线追迹时会模拟设置阈值、随机光线数、随机乱数种子，所以在Tracepro 软件计算过程中，机械结构组件的散射情况也会添加到隔离效果的计算中，导致两种方法存在一定差别。

图8 不同表面粗糙度下的端机隔离度曲线Fig.8 Isolation curve under different surface roughnesses

图9 不同表面粗糙度端机隔离度Matlab 曲线Fig.9 Matlab curve of end machine’s isolation with surface roughness

4.3 系统中镜面污染对端机隔离度的影响

对镜面污染仿真首先假定镜面的污染分布均匀，且颗粒之间的间隔远大于颗粒半径。在TracePro 中设置如表3 所示的元件表面ABg 模型，改变清洁度水平，以分析不同污染程度对端机内隔离度的影响。在进行分析时各表面粗糙度均设置为5 nm。由公式(6)可计算出表面粗糙度为5 nm 对应的TIS 数值为1.61×10-3，ABg 模型参数A=1.152×10-4。图10 为清洁度分别为200、400、600、800 时TracePro 仿真得到光通量图。TracePro 中同样设置发射总光线数70 万，总光通量为1 W，光线追迹阈值为1×10-7。

图10 不同的清洁度水平端机接收面光通量。（a）CL=200；（b）CL=400；（c）CL=600；（d）CL=800Fig.10 The luminous flux of the receiving surface with different contamination levels.(a) CL=200; (b) CL=400; (c) CL=600;(d) CL=800

通过图10 光通量可计算出在不同清洁度水平下激光通信终端内部的隔离度，如折线图11所示。由图11 可知，在各个元件参数相同的情况下，λ/2 波片、λ/4 波片及光学天线的表面清洁度水平不断下降，导致激光通信终端内的隔离度不断下降，CL=800 时低至37.37 dB。图12 为Matlab 软件根据式(13)、式(21)绘制的不同清洁度水平下的隔离效果变化曲线。通过两种模型的对比可以看出表面清洁水平在CL=200 至CL=800 之间激光通信终端的隔离效果变化趋势基本一致。两种方式的仿真结果同样存在一定偏差。这是由于Matlab 软件是根据公式中的变量进行绘图的，不考虑终端中其他机械结构对隔离效果的影响，对Tracepro 软件进行仿真绘图时整体端机模型均进行仿真计算，散射、反射因素会影响系统的隔离效果。

图11 不同清洁度水平的隔离度曲线Fig.11 Isolation curve of different contamination level

图12 不同清洁度水平的隔离度Matlab 曲线Fig.12 Matlab curve of isolation with different contamination levels

4.4 激光通信终端隔离效果双因素分析

在光学系统的实际工作中，表面粗糙度与表面污染程度变量会相互作用，这应该加以考虑。因此，本文深入探讨了表面粗糙度与表面污染程度对激光通信终端通道隔离的影响。

激光通信终端通道系统中的反射系数设置为0.99，偏振分光棱镜的消光比设置为0.001，θi设置为0.02 rad，考虑到非理想情况下表面清洁度水平设置为CL=200 至CL=800，表面粗糙度设置为0.5 nm 至15 nm 之间的值。通过在上述范围内改变这两个影响因素，分析了隔离对其变化的敏感性，并绘制了在实际工程中可实现的隔离效果变化曲面图，如图13 所示。x轴表示不同的表面粗糙度、y轴表示不同表面清洁度水平、z轴表示隔离度。两个变量(即表面粗糙度σ和表面污染程度)对隔离的交叉影响相同，但隔离范围不同。具体来说，使用1 550 nm 的工作波长，激光通信终端通道隔离范围为27.93～86.49 dB。

图13 激光通信终端隔离度双变量分析图Fig.13 Two-variable analysis diagram of laser communication terminal isolation

本节分析的实际意义在于，在单波长的激光通信终端设计中，根据获得的隔离特征曲面图，优化终端隔离效果，可在表面粗糙度和表面污染程度之间权衡，取得最佳值。

4.5 优化参数提升隔离度

本激光通信终端发射功率为33 dBm，通信接收机灵敏度为-45 dBm@10 Gbps，根据4.4 节双变量分析结果，对仿真模型进行优化。如图14(彩图见期刊电子版)所示。表面粗糙度为固定值时。由于表面清洁度水平CL=300 至CL=400 间的跳跃幅度较大，而本文中激光通信终端的光学元件应使其清洁度水平低于300。

图14 不同表面清洁度BRDF 曲线Fig.14 BRDF curves of different contamination levels

表面粗糙度为0.5 nm 时，ABg 模型中B、g参数仍分别为4.441 5×10-5、1.55，确定A值为1.183 7×10-6，光学天线的主次镜对应的ABg 模型中参数A分别为8.512 1×10-7、1.123 0×10-6。对此参数进行仿真分析，结果如图15 所示，此时的隔离度为78.35 dB。达到了基本的指标要求。

图15 粗糙度为0.5 nm 端机接收面光通量Fig.15 Terminal’s receiving surface light flux with surface roughness of 0.5 nm

5 实验验证与测量

本节根据图6 软件模型结构设计了通信终端模型，将根据设计的通信终端模型来验证4.5 小节仿真计算得到的发收隔离度。整体测试环境如图16 所示。

图16 隔离度测试端机Fig.16 Isolation test setup

在测试中镜片表面粗糙度小于1 nm，偏振器件的消光比为1 000∶1。在测试过程中，激光放大器输出不同功率的激光束，测量探测器接收的光束功率，如表5 所示。当输出功率不同时，测量探测器接收到的杂散光功率，并计算通信终端的隔离度。通过测量，其平均隔离度为77.86 dB。使用所建立的模型仿真的隔离度为78.35 dB。测量值与计算结果的差值为0.49 dB。通过详细分析端机和测量过程，通信接收机的灵敏度为-42 dBm，存在误差。因此，可以判断测量结果与仿真结果基本一致。

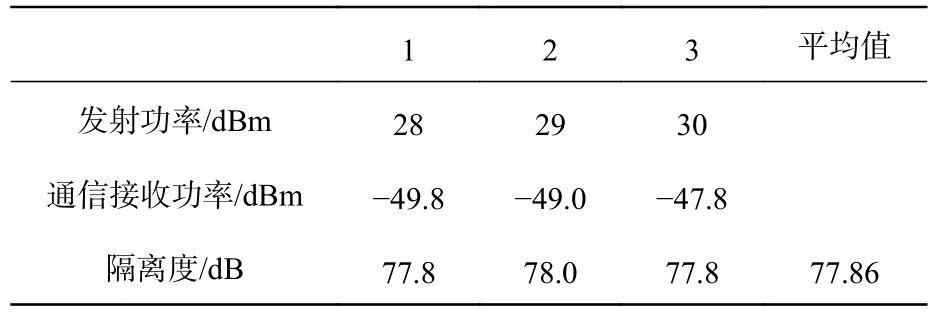
表5 隔离度测试结果Tab.5 Test results of isolation

6 结 论

本文设计了一种单波长的激光通信终端信道，分光结构选用56°偏振分光棱镜代替常用45°偏振分光棱镜，减少部分杂光信号对探测器的影响。并通过设置不同的λ/2 波片、λ/4 波片、光学望远单元中离轴抛物面、离轴反射镜、准直透镜组的表面粗糙度和元件清洁度水平模型数据来优化光学系统。利用TracePro 平台对激光通信终端模型进行相关仿真。根据模拟结果可知：λ/2 波片、λ/4 波片、光学望远单元中的离轴抛物面、离轴反射镜、准直透镜组的表面粗糙度影响着隔离度水平。随着粗糙度增大，隔离度逐渐变小。同时，在同等条件下的模拟结果显示，随着各个镜片的表面清洁度水平的增大，激光通信终端内隔离度也会逐渐降低。因此，为了保持激光通信终端内的隔离度，应严格控制表面粗糙度，并且在进行系统安装时应保证各元件表面清洁度水平。最后，根据各个元件镜片表面粗糙度为0.5 nm 时，激光通信终端内部探测器隔离度为78.35 dB 的仿真结果建立了通信终端实体模型。测量的隔离度实际平均值为77.86 dB，与模型仿真结果基本一致。上述结果验证了模型仿真准确性。