基于CFD的输油管道腐蚀特性分析

李 明，蔡 亮，李 杉，李小刚，张世强，梁昌晶

（1.中国石油华北油田分公司第五采油厂，河北 辛集 052360； 2.中航油京津冀物流有限公司，天津 300300； 3.中国石油渤海装备巨龙钢管公司，河北 青县 062650；4.中国石油渤海钻探工程有限公司井下作业分公司，河北 任丘 062552）

0 前 言

近年来，因腐蚀造成的输油管道泄漏穿孔事故频繁发生。在腐蚀类型分析中，内腐蚀和土壤腐蚀与大气腐蚀相比，具有腐蚀速率快、隐蔽性强等特点，是导致管道失效的主要原因[1-3]。由于原油无导电性，且管壁具有润湿性，当原油不含水时，不具备腐蚀性，而当原油含饱和水或游离水时，因重力作用，水相沉积在管道底部，与管壁形成电化学腐蚀环境，可加快腐蚀的发生。因此，掌握管道中油水两相的分布情况，对于预测管道腐蚀程度具有重要意义。

计算流体力学（computational fluid dynamics，CFD）方法由于计算精度高、再现性好等优点，被广泛用于油水两相流动的研究[4-5]。樊文娟等[6]对不同体积流量、含水量和曲率半径下的含水原油腐蚀性进行了研究；张洋洋等[7]将CFD与OLGA软件相结合，得到了段塞流和流型转变处的腐蚀速率较大的结论；程振玉等[8]对油水两相流体系下的腐蚀行为进行了研究，认为流速和含水率对腐蚀影响较大。以上研究多为定性分析，对管道腐蚀性进行定量分析的研究较少，无法用于指导现场防腐措施的制定。基于此，本研究利用Fluent软件，基于VOF欧拉模型和k-w湍流模型，对油水两相体系下不同含水率、流速下的管道积液情况进行了分析，为临界流速的确定和内腐蚀直接评价技术的拓展提供实际参考。

1 模拟参数与方法

1.1 数学模型

由于涉及油水两相的非稳态流动，为观察两相界面的分布情况，采用VOF 模型(volume fluent model)进行计算分析，动量守恒方程为

质量守恒方程为

式中：ρ——流体密度，kg/m3；

u——流体流速，m/s；

p——压力，Pa；

μ——黏度，mPa·s；

F——两相表面张力，mN/m；

t——时间变量，s；

αq—q相的体积，m3，q为油相或水相。

由于管内的雷诺数较大，属于湍流流动，故采用k-w湍流模型模拟不同相态的流动过程，即

式中：k——湍流动能，m2/s2；

ω——湍流耗散率，m2/s3；

Pk——湍流动能生成项，由速度梯度产生；

Pkb——湍流动能源项，由浮力产生；

Pwb——湍流耗散率源项，由流体扩散产生；

t——时间变量，s；

xj——第j个坐标方向；

β、β′、α、σk、σω——常数。

1.2 多相流模拟参数设定

采用Design Modeler 软件进行二维建模，采用Meshing 软件进行网格划分。为了计算简便，利用二维流场模拟，选择结构化网格划分，在壁面处适当添加边界层，并对管口两侧进行网格加密，划分结果如图1 所示。模拟条件见表1。

表1 多相流模拟条件

图1 网格划分示意图

1.3 初始和边界条件

为了让流型得到充分发展，减少迭代过程造成的数据波动，进行如下假设：①假设流体不可压缩；②模拟过程中的温度波动对流体流动的影响忽略不计；③忽略流体与管壁之间的粘性力，忽略滑移作用；④不考虑各相之间的传质和相变。

采用VOF 模型跟踪油水两相的界面位置，通过求解相连续方程完成分界面位置的确定。将油相定义为第一相，水相定义为第二相。入口处采用速度边界，出口处采用压力边界。在保证各项收敛精度的前提下，采用Second Order Upwind离散求解方式，步长为0.005 s，每步最大迭代次数为100，共计1 000 个时间步长。采用Hybrid的方式进行初始化，通过拉普拉斯方程求解计算域中压力场和速度场的初始分布情况。

2 模型验证

2.1 网格独立性验证

为保证计算结果不随网格的细化而变化，在含水率30%、流速0.05 m/s 的条件下，测试了不同网格下的最大壁面剪切应力，结果见表2。

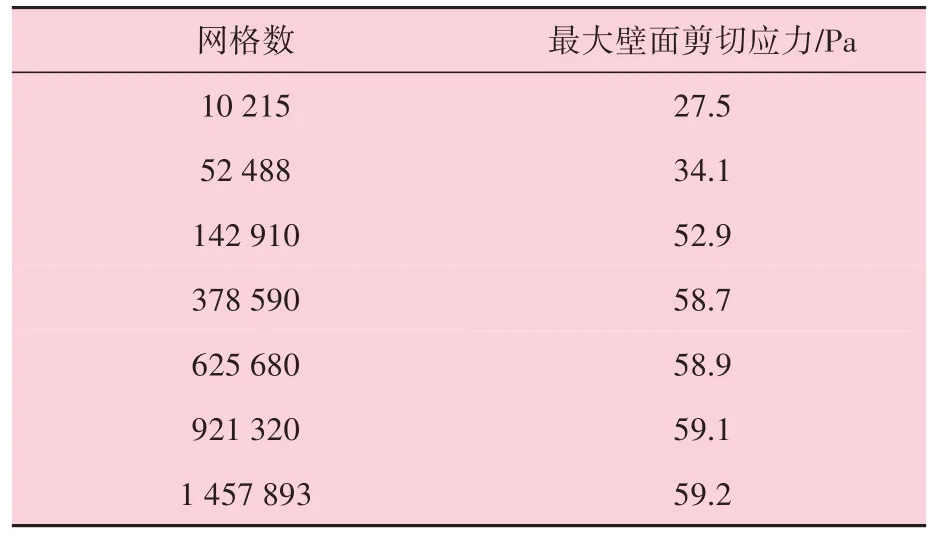
表2 网格独立性验证

当网格数小于142 910 时，无法得到最大的壁面剪切力；当网格数为378 590 及以上时，最大壁面剪切力基本保持稳定。为兼顾计算速度和计算精度，选择网格数为625 680进行后续计算。

2.2 流型验证

为验证CFD 数值模拟的准确性，参照Taitel和Dukler关于气液两相流型的划分方法，将油水两相流型分为分层流、油包水分散流和水包油分散流，模拟结果如图2 所示。其中，红色为油，蓝色为水，黄色为油水混合物。

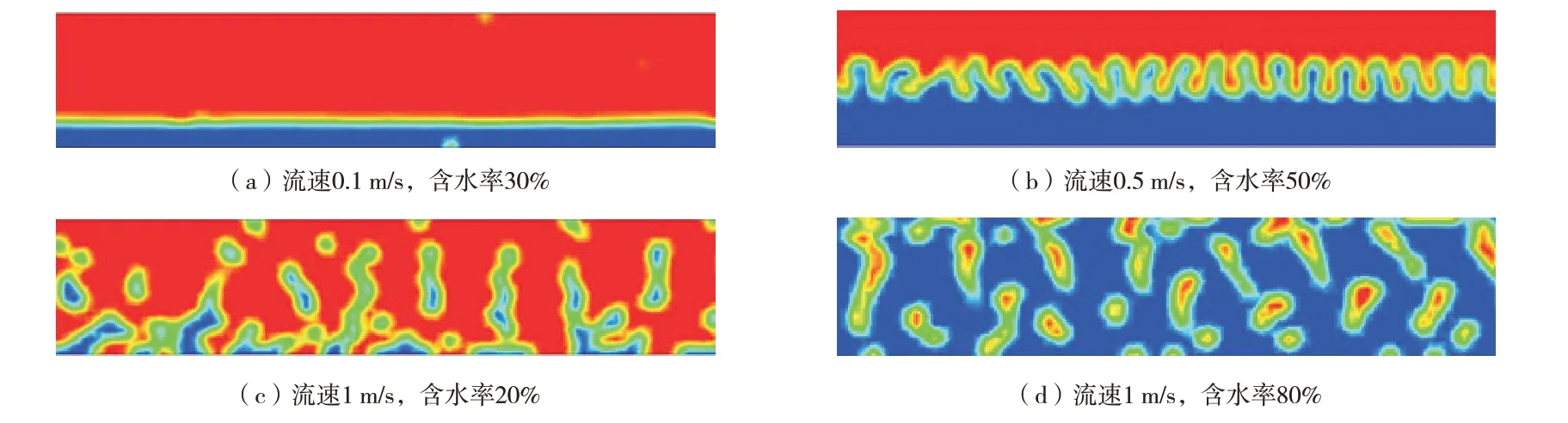
图2 不同条件下的流型模拟结果

在流速0.1 m/s、含水率30%时，流型为分层流（图2（a））；在流速0.5 m/s、含水率50%时，流型为波浪流（图2（b））；在流速1 m/s、含水率20%时，流型为油包水分散流（图2（c））；在流速1 m/s、含水率80%时，流型为水包油分散流（图2（d））。可见，流速和含水率决定了流型转变和流相分布特征，其结果与文献[9]中的试验结果基本一致。此外，根据Ostwald 的乳状液转相观点，当含水率小于26%时，只可能形成油包水型乳状液；当含水率超过74%时，最大可能形成水包油型乳状液。因此，采用CFD方法预测油水两相流的分布特征，进而描述管内积液情况和腐蚀强弱具有一定的科学性。

3 结果与讨论

3.1 含水率对积液的影响

原油中只有含有一定量的游离水，当管道底部润湿时才会发生腐蚀。根据GB 50350—2015《油田油气集输设计规范》中关于原油经济流速的规定，分别考察低流速（0.5 m/s）和高流速（1.5 m/s）条件下，不同含水率的流相分布特征，如图3 和图4 所示。当流速较低时，无论含水率或低或高，管道底部均形成一层积液，不同的是含水率高的管道，形成的积液厚度更大，说明此时的原油流速不具备携水性。当流速较高时，在含水率为5%和20%的条件下，管道底部不形成连续水相，说明此时的原油流速具备携水性；在含水率为40%和60%时，由于水量较大，原油中的水被夹带并分散在原油中，造成管底和管顶形成部分连续水相，腐蚀性增强。综上所述，只有在低含水高流速的条件下，管道的腐蚀性才较弱，流速对积液的影响较含水率更强。

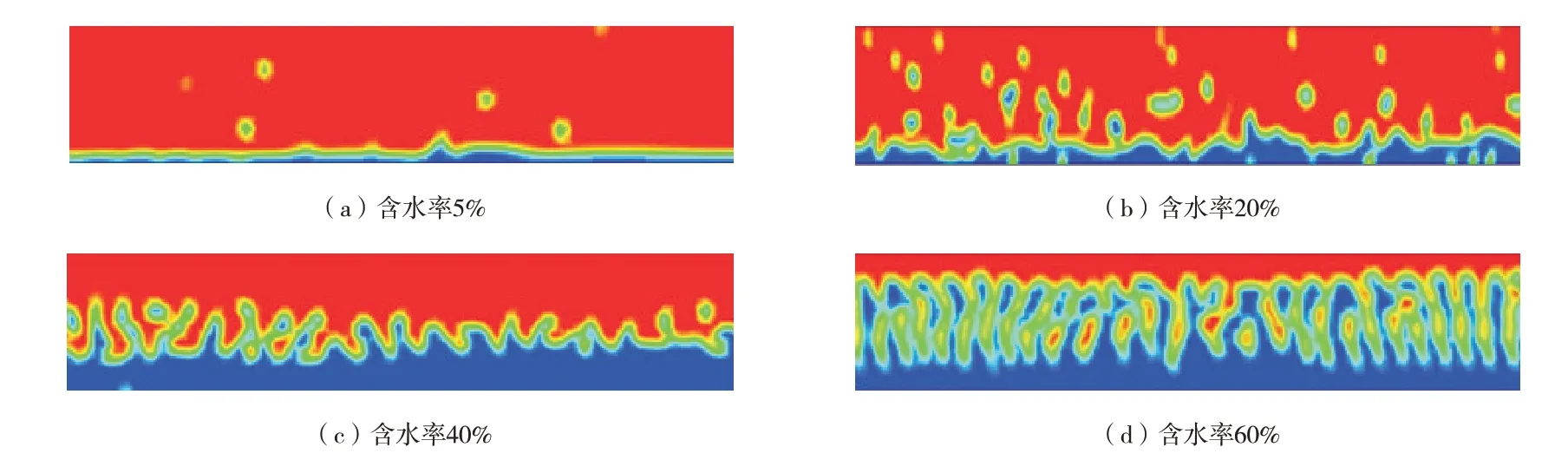
图3 低流速（0.5 m/s）下不同含水率的流相分布特征

图4 高流速（1.5 m/s）下不同含水率的流相分布特征

3.2 流速对积液的影响

在含水率20%的条件下，考察不同流速的流相分布特征，结果如图5所示。随着流速的增加，管内流型从分层流（0.2 m/s）向分散流（2.0 m/s）转变，水在管道中的离散现象加强，不会形成积液，管道内壁被原油润湿保护，腐蚀性逐渐减弱。为了让流型在管内充分发展，取3 m 处管道的径向截面，做径向截面-含水率的散点图，如图6所示。其中，横坐标0点代表管道中心，0点以上代表管道中心到管顶的距离，0 点以下代表管道中心到管底的距离，横坐标的取值范围为（-0.084，0.084）。

图5 低含水率下不同流速的流相分布特征

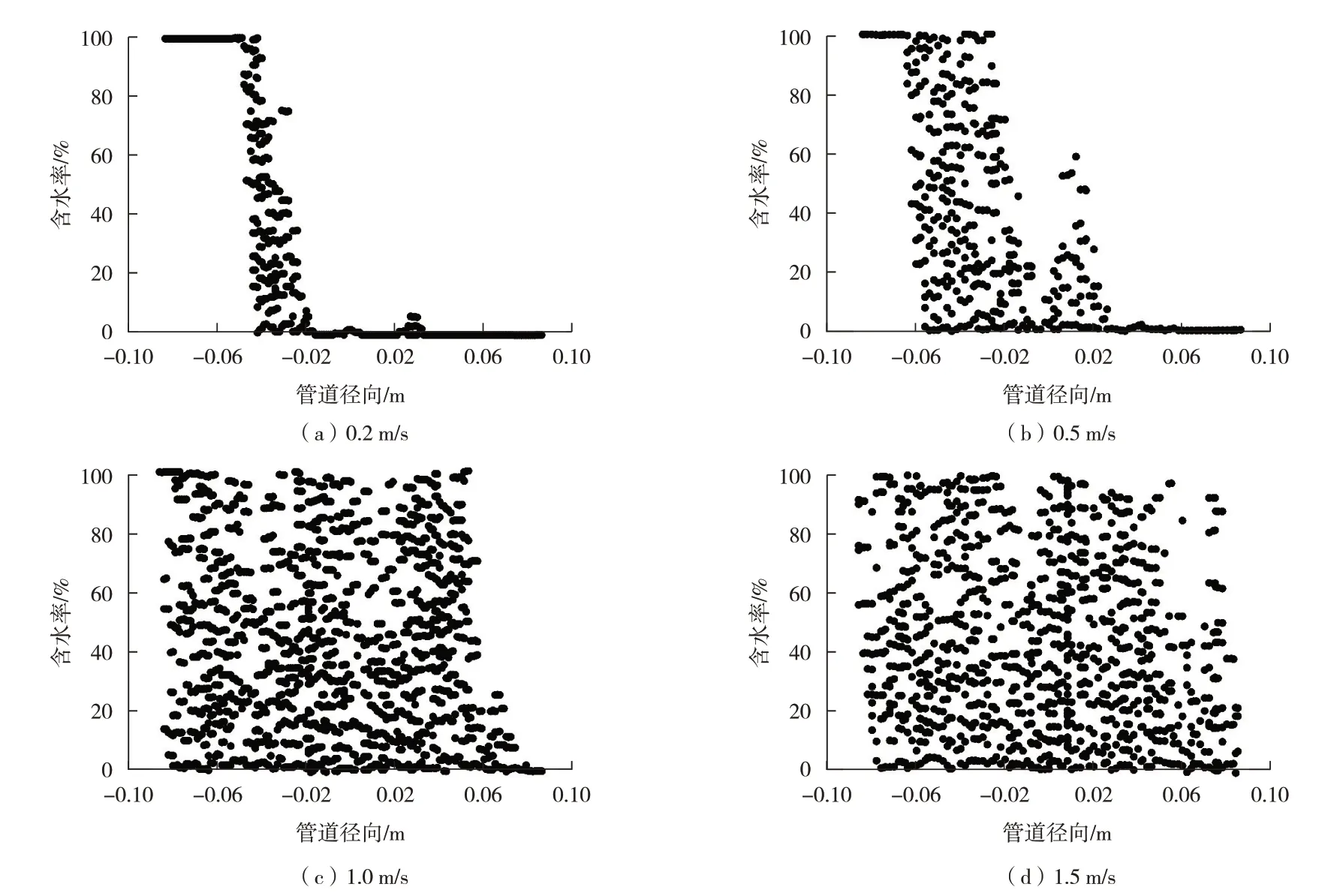
图6 不同流速下管道径向截面-含水率散点图

从图6可以看出，流速为0.2 m/s时，管底积液较厚，管顶无游离水；流速增加至0.5 m/s时，管底积液厚度进一步减小；流速增加至1.0 m/s 时，管底几乎无连续的离散点，说明此时管底没有连续水相存在，此时的速度即为临界流速。当原油流速低于临界流速时，腐蚀严重；反之，腐蚀较轻。

3.3 原油密度对临界流速的影响

参照图6的表示方法，考察不同原油密度下的临界流速，结果如图7所示。从图7可以看出，原油密度越大，所需的临界流速越小，当原油密度大于800 kg/m3，临界流速减小的速度变缓。这是由于原油密度越大，水相受重力及黏性作用的效果越弱，原油的携带作用越强，管内流型越容易形成分散流型。

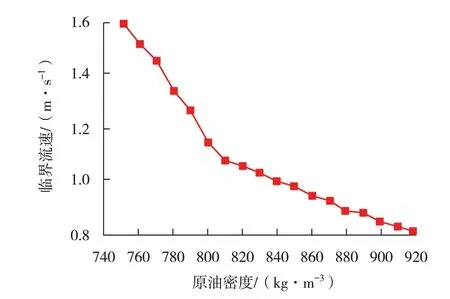
图7 原油密度对临界流速的影响

3.4 温度、压力对临界流速的影响

同理，考察不同压力、温度对临界流速的影响，结果如图8所示。从图8可见，随着压力的升高，临界流速不断增加，压力从0.2 MPa 升高至2.2 MPa，临界流速增加了34%，但变化幅度远小于原油密度；随着温度上升，临界流速呈上下波动，说明温度与临界流速之间无明显关联，这与模拟时未考虑温度对流动特性的影响有关。相关研究[10-11]也表明，在温度＜60 ℃时，温度不会对腐蚀产物膜产生影响，因此温度对腐蚀的影响较小。

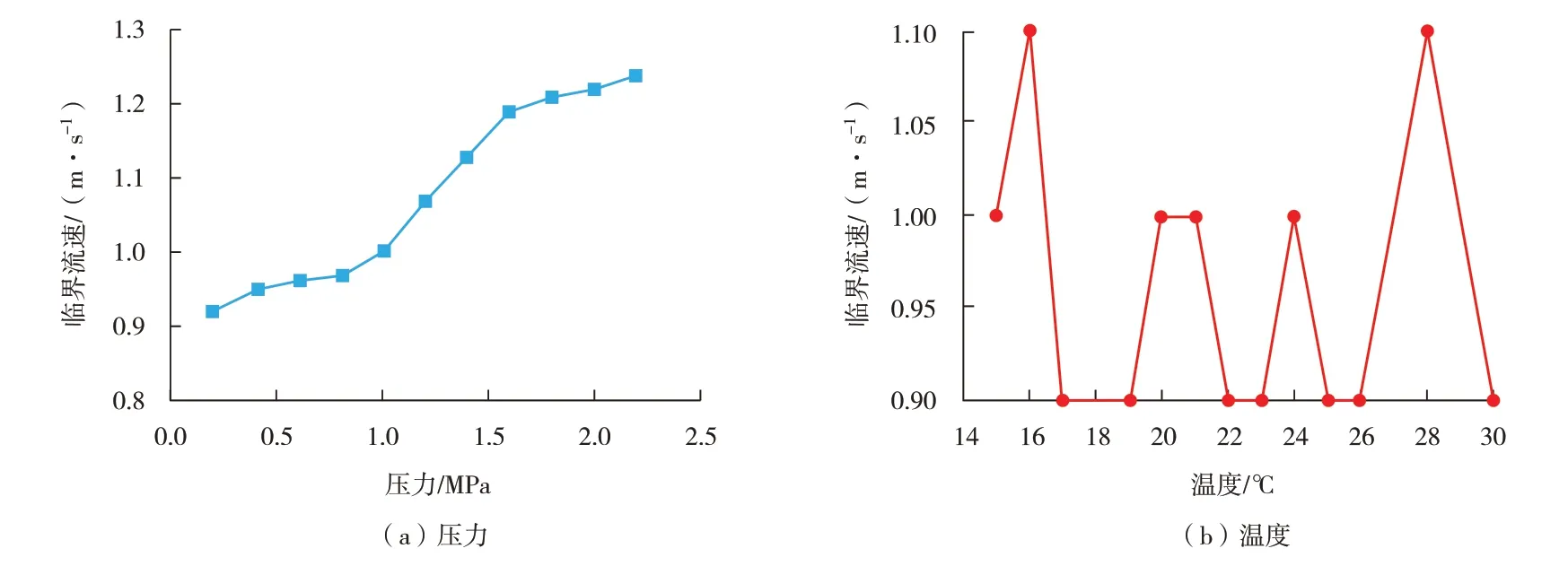
图8 压力、温度对临界流速的影响

4 结 论

（1）在网格划分和边界条件设置合理的基础上，采用CFD预测油水两相流的分布特征，可实现分层流、油包水分散流和水包油分散流等流型的模拟仿真，证明了CFD方法的科学性和准确性。

（2）对于低含水原油，流速越大，原油对水的离散作用越强，腐蚀危险性越弱；对于高含水原油，无论流速大小，管壁处均会形成连续水膜，腐蚀危险性增大。

（3）流速增加会降低管底积液厚度，当管底几乎无连续含水率离散点时可确定临界流速，当原油流速低于临界流速时，腐蚀严重；反之，腐蚀较轻。

（4）原油密度、压力对临界流速有一定影响，而温度与临界流速之间无明显的关联特征。