铷簇同位素效应的量化研究

邸淑红 张阳 杨会静† 崔乃忠 李艳坤 刘会媛 李伶利 石凤良 贾玉璇

1) (唐山师范学院物理科学与技术学院,唐山 063000)

2) (中国气象科学研究院,灾害天气国家重点实验室,北京 100081)

3) (唐山师范学院化学系,唐山 063000)

针对簇类同位素位移难以测定及其产生原因难以鉴别等问题,本文运用光磁共振和热离解相结合的技术,获得了气态Rb 同位素原子簇87,85Rbn (n=1,2,···,13)两系列共振离解光谱、等数簇矩移、塞曼能移.并对每个簇进行基于巨原子概念模型量化计算,其结果与实测结果严格一致,表明铷簇可以作为巨原子分析.进一步运用铷簇塞曼能级间隔公式计算出87,85Rbn (n=1,2,3,···,92) 5s 电子壳层能级结构,发现5s 单电子壳层结构主要秩序和步距与钠簇的在球状对称势阱下3s 单电子壳层结构相似,证实铷簇5s 单电子壳层结构可以由塞曼能级大能隙决定.共振离解光谱的奇偶交替特性及其在特殊数(如n=2)处的反常磁矩特征峰均是由价电子的内在性质和分子结构特性引起.还发现87Rbn 与85Rbn 的5s 单电子壳层结构步调严格一致,量值大小均有3/2 比值关系,且二者光谱中心频率及展宽存在反常差异,可能与87,85Rb 的核素处于核壳层闭合面附近直接相关.

1 引言

前人对铷同位素87Rb,85Rb 分离及效应的研究方法主要分为两类: 光化学分离研究法和质谱分离研究法[1,2].由于87Rb,85Rb 两种原子能级结构不同导致两同位素吸收光谱频率不同,光化学分离研究法是指以此作为参考依据进行的同位素分离研究方法.光化学分离技术比传统的单原子蒸汽激光同位素分离技术(AVLIS)在规模上具有较强优势[3].研究者们对铷的兴趣取决于其在高科技和精确光谱测量中的应用,特别是从天体物理联合研究所JILA 和康斯坦茨大学提出并建造4 个二极管激光器[4,5],成功通过衍射光栅的角度调节,实现了约10 nm 的激光调谐范围后,人们对铷的研究兴趣越来越浓厚.87Rb 同位素现已被国际公认为二级原子频标和同位素物质参考的标志性元素[6].在2003 年,Makarov 等[1]使用光过滤法对85Rb,87Rb 同位素进行选择性地激发,测量其稀释物85Rb35Cl+,87Rb35Cl++85Rb37Cl+和87Rb37Cl+对应的峰值浓度比率,从光未过滤的7.7∶5.6∶1.0 到光过滤后的1.8∶3.5∶1.0,实现了光过滤定性分离同位素的可能性.质谱分离研究方法是以两个同位素87,85Rb 的原子质量不同作为主要参考指标,对稀释物质中两个同位素原子摩尔数之比进行精确测量的方法[6-8].2002 年,Waight 等[9]提出了MCICPMS 方法,即用混合了锆90Zr/91Zr 的探针测量87Rb/85Rb 原子摩尔数之比的方法,修正87,85Rb 同位素稀释物在热电离质谱中的质量分馏效应偏差.在此技术基础上,Nebel 等[10]采用混合了锆的92Zr/90Zr 探针对87Rb/85Rb 的质量分馏量偏差进行校正.此单项分析过程中,87Rb/85Rb 测量值的外部再现标准偏差仅为0.02%–0.05%(2 S.D.)[9,10],比传统热电离质谱技术测量精度提高了10 倍以上[7,10].

与此同时,对于碱金属簇ns 电子壳层结构的研究也在逐步展开,特别是对Nan,n=1–92 电子壳层结构进行了深入的研究[11].Knight 等[11]用球对称势模拟了团簇内3s 电子有效单电子势,用薛定谔方程的能量本征值计算出钠簇Nan,n=1–92 结合能的3s 单电子壳层结构,将其主要秩序和步距与钠簇质谱对比,发现与质谱丰度的主要秩序和步距相协调一致,闭壳层处特征明显.1987年,巨原子概念模型被证明对钠簇电子结构有效[12].基于其他碱簇在最简单的球状对称势阱下的模型[12],推测它们的ns 电子壳层结构也应与钠簇相似[13].Igarashi 等[14]还讨论了27Al 和87Rb 在核磁共振实验中Rb 型沸石的电子构型特征,并与K 型沸石进行比较,通过磁源观测分析27Al 光谱的展宽,指出铷簇光谱的形状与K 簇情况的差异.这些事实表明,Rb 原子簇和K 原子簇的电子构型并不相同,在温度10 K 以下,87Rb 谱心明显向更高的频率移动,证实5s 电子和Rb 核之间存在费米接触相互作用能.

综上可知,由于85Rb 和87Rb 分馏效应及其稀释物分离过程的复杂化限制,前人对铷同位素的光化分离和质谱分离研究主要停留在对其稀释物中85Rb,87Rb 同位素的定性分离上,而对二者原子簇85Rbn和87Rbn5s 电子壳层结构区别的辨识及其相应同位素效应的量化研究还未见到相关详细报道.

本文主要是在前一篇铷簇87Rbn,n=1,2,3,···,15,磁矩实验观察及理论分析的基础上[15],对87,85Rbn两同位素效应进行量化研究.计算了等原子数同位素原子簇(isonumber clusters,简称等数簇)的磁矩平移(magnetic moment shift,简称矩移),塞曼能级间隔平移(Zeeman energy shift,简称塞曼能移),并进一步扩大n的计算范围,用塞曼能级间隔公式推算出了87Rbn,85Rbn的5s 电子壳层结构,并阐释了显著同位素效应产生的原因.

2 实验过程

本文采用光磁共振技术和热离解技术相结合的方法,用连续射频扫描磁场中的气态铷簇使其共振,铷簇在共振激发态或回落的过程中由于原子光谱D1σ+辐照或与其他分子碰撞而热离解,并产生单原子.再用单原子光谱D1σ+光对其进行抽运探测,形成两系列87Rbn,85Rbn共振离解光谱(resonance dissociation spectra),以下简称光谱.

本研究所用仪器及实验方法与北京大华无线电仪器厂的光磁共振实验装置及方法基本相同[16],实验样品制作过程和仪器精度及工作环境与测量87Rbn的要求相同[15],只是强调必须保证样品的工作环境温度达到328–333 K (55–60 ℃),实现kT大于 Rb2双原子簇激发态的离解能[17],估算出87,85Rb2激发态的离解能是基态87,85Rb2离解能48.898 kJ/mol 的1/20–1/10[18],其中k为玻尔兹曼常数,T为铷蒸汽样品的工作温度.借用在结构化学中多原子分子键能键长排序的讨论中,关于Jahn-teller 效应引起的原子间键长的变化的作用[19,20],可知对于同一元素的双原子分子组成的共价键直线型原子间键长小于3 个原子组成的三角形结构的原子间键长,因此87,85Rb2的离解能大于87,85Rb3,此外,对于同一元素且均含有一个单键的奇数个原子组成的簇聚类分子所含的原子个数越多离解能越低,即87,85Rb3的离解能大于87,85Rb5,7,9,11,13,如文献[11]钠簇质谱中呈现出的偶数簇的丰度(或结合能)总高于相邻近奇数簇丰度(结合能),且总趋势是随n递增而递减的规律一样[11],因此只要工作温度T能够实现kT大于Rb2双原子簇激发态的离解能[17,18],就能观测到87,85Rb2产生的共振离解光谱,那么就一定能观测到其他奇数簇的共振离解光谱.当然,对于密闭低压情况下的氮载气的铷簇分子的解离和复合过程是一种十分复杂的热力学动态平衡过程[17],尚待更深入的进一步研究.

实验中获得85Rbn(n=1,2,···,13)各簇粒子磁矩值的过程与测量87Rbn(n=1,2,···,13)磁矩的相应过程相似[15],只是在测得87Rbn(n=1,2,···,13)各簇粒子的磁矩及光谱后,再继续从85Rb1开始测量85Rbn(n=1,2,···,13)系列簇粒子磁矩值及光谱,同时记录两大系列87Rbn,85Rbn原子簇在相应磁场H0下的共振频率f和相应光谱的振幅A及其他特征信息.详细数据情况及光谱信息参见相关补充材料S (online).

3 数据与光谱

3.1 数据规律及分析

两同位素磁矩曲线如图1(a)和图1(b)所示(具体数据见补充材料SC 和SD (online)),可以看出,两系列同位素原子簇的磁矩曲线宏观上具有一致性,共振频率与磁场成直线关系,恒定的直线斜率值代表每个原子簇的磁矩是一个恒定值,不随外磁场而变化,可称其为原子簇的自发磁矩,奇数87Rb 簇的自发磁矩均大于相应等数簇85Rb 的自发磁矩.除n=2 与奇数簇规律一致外,其他偶数簇磁矩均为0 .

图1 (a),(b)实验测得的87Rbn, 85Rbn 的8 种簇粒子的共振频率 与磁场H0 的关系曲线(1 G=10-4 T)Fig.1.(a),(b) Relationship between the resonant frequency of 8 kinds of 87Rbn,85Rbn cluster particles and the magnetic field H0.

再提取补充材料SC 和SD (online)中87Rbn,85Rbn的13 对等数簇平均磁矩和振幅,见表1,可以看出,两个同位素原子簇的磁矩和塞曼能级间隔随n的递增呈奇偶交替变换模式,奇数的磁矩和塞曼能级间隔随n递增而递减,奇数的振幅幅度也呈递减趋势.每个簇的平均振幅值代表每个簇相应的解离出单原子分子的浓度,如果有光磁共振离解现象的每个簇的离解率均为100%,那么振幅就代表在样品中含有的每个簇的浓度,偶数簇除了n=2 之外,其余簇幅值均为0,没有离解现象.由图1 和补充材料SC,SD (online)的磁矩平均值规律性,可以分别写出87Rbn,85Rbn的等数簇(包括n=2)实验公式:

表1 实验测量的87Rbn, 85Rbn 等数簇平均矩移和塞曼能移及光谱振幅Table 1. Measured mean magnetic moment shifts,Zeeman energy shifts and spectrum amplitudes of 87Rbn, 85Rbn.

3.2 光谱规律及分析

依据实验测得共振解离光谱原图的形态及振幅平均值,按比例画出了两系列同位素原子簇的87,85Rbn(n=1,2,···,13)的共振离解光谱图2(a)和图2(b) (具体数据见表1 及补充材料SA,SB(online)).

图2 (a),(b) 两系列同位素原子簇的87Rbn, 85Rbn (n=1,2,···,13)的共振离解光谱Fig.2.(a),(b) Resonance dissociation spectra of two series of isotopic atomic clusters 87Rbn, 85Rbn (n=1,2,···,13).

由实验数据(补充材料SB (online))得知,87,85Rb两系列同位素原子簇的光谱幅度随磁场的变化规律宏观上具有一致性.在外磁场一定时,幅值均随原子数n在1,2,···,13 连续递增而呈现奇偶交替变化规律.奇数簇的光谱幅值是随n递增而递减.当外磁场在2.376257–4.752514 G 内逐渐增大时,每个簇相对单原子幅值比保持不变且均逐渐减小,绝对幅值约有50%的减小.偶数簇除在n=2 处出现一个反常信号外,其他偶数簇磁矩为0[21],无共振幅值,由此证明奇数簇共振前是稳定的簇分子,偶数簇(除n=2 外)连续扫频未见其共振解离现象发生,证明其更稳定.

由于磁场的改变,簇光谱表现出的奇偶交替及一致性变化规律表明,共振离解光谱中的峰和n=2反常阶跃是由铷团簇5s 电子的磁矩性质和分子结构特性造成的[19,20],也反映出团簇的结合能在解离过程中起到了很重要的作用[14],奇数簇由于结合能较低,共振后的激发能级不稳定或在跃迁回落过程中由于光照和碰撞被解离出单原子[15,17],这也是我们称样品为85,87Rb 单原子气体的原因.鉴于碱簇的巨原子特性和实验中奇数簇的离解特性[12,17],可粗略地认为奇数簇是由一个含有比它少一个原子的偶数簇,即含有偶数个5s 价电子的稳定非闭合壳层能级的大原子和一个单原子簇合而成的双原子分子,又可认为是一个含有相应奇数个5s 价电子的稳定非闭合壳层结构的大原子.

4 模型计算与实验结果比较

4.1 簇分子电子组态与分子项型表

从以上分析可知,偶数簇除n=2 外,磁矩均为0[19-21],n>2 的奇数簇可粗略认为是双原子分子,即由一个稳定的非闭壳层结构且含有偶数个5s 价电子的大原子和一个铷单原子簇合而成的双原子分子.根据铷核间距大小及其相关双原子分子的洪德情形(a)的跃迁规则,参照相关文献[15,17]中的双原子分子的电子态项型表,列出了85Rbn或87Rbn的n=1,2,3,5,7,9,11,13 的8 对等数簇的双原子分子的电子组态和分子项型表,簇的价电子能级用双原子分子轨道特征值λ合及自旋角动量s的本征值来表示,详细内容见表2[15,17],其中Hund(a)跃迁规则为 ∆λ=0,±1;g↔u;∆n=0,±1;∆s=0.

由表2 可以看出奇数簇均为双重态分子,而且稳定性判别值Pa-Pb均为1/2 的整数倍,证明这些分子均是顺磁的二重态费米子,且第一激发态与基态均有同样的稳定性.只有87,85Rb2的判别值Pa-Pb为0 整数,是一个三重态的线性顺磁玻色子的特例[17,19,20].由于发生塞曼共振跃迁信号很弱而不可见[17],∆g以上的分子态不能稳定不可见,只有2Πu,2Πg,3Πg塞曼跃迁共振信号稳定可见.

4.2 原子簇磁矩和塞曼能级间隔模型与实验结果比较

与文献[15,17]的计算分析过程相同,得出8 对87Rbn,85Rbn的2Πu,2Πg,3Πg分子态的双原子分子磁矩简写公式:其中λ合=1,Σ是分子中的价电子的合自旋s在分子核间轴上的投影,Σ=s,s－1,s－2,···,－s,并且Σ的大小与分子是独态或多重态相关,又因为多重态分子的塞曼裂距与独态塞曼裂距完全相同,所以,一般忽略Σ的作用,认为Σ=0;µ0=µB,µB为玻尔磁子;取分子磁量子数M=MFmax=F合,MF=F合,F合－1,F合－2,···,－F合,这里F合为分子超精细结构的合角动量.那么,对于87Rbn的每个原子核自旋量子数Ip=3-/2,基态轨道量子数L=0,自旋角动量s=1/2,轨道与自旋耦合形成原子的精细结构原子角动量J=L+s=1/2,单个原子超精细结构的合角动量F=Ip+J=3/2 +1/2=2;簇分子的合角动量为F合87=nF=2n;而对于85Rbn核自旋由价质子的1f5/2能级态来表征,Ip=5-/2,相应每个原子基态精细结构角动量为J=1/2,超精细结构的角动量F=Ip+J=5/2+1/2=3,簇分子角动量F合85=nF=3n.由此,参考文献[15,17]可写出87Rbn和85Rbn的模型简化磁矩公式:

其中87Rbn和85Rbn朗德因子分别为g87n=1/(2n)和g85n=1/(3n) .

根据(7)式和(8)式可得87Rbn和85Rbn的塞曼能级间隔模型公式分别为

等数簇磁矩矩移公式为

等数簇塞曼能移公式为

用(7)–(10)式对n=1,2,···,13 的两同位素原子簇的磁矩和塞曼能级间隔进行计算,并将模型计算结果与实验结果对比,分别见表3 和表4.

表4 85Rbn 磁矩和塞曼能级间隔模型与实验结果比较Table 4. Comparison of experiment values and calculated values of magnetic moment and Zeeman energy level interval of 85Rbn atomic cluster.

由表3和表4可以看出,87Rbn,85Rbn实验与模型的矩移和塞曼能移相对误差仅为-6.989‰和-5.8‰,两个均不足1%,数值上每个铷簇电子能级结构自洽于巨原子模型的结果.

4.3 等数簇矩移和塞曼能移模型与实验结果比较

采用(7)–(12)式对n=1,2,···,13 的两87Rbn和85Rbn的矩移和塞曼能移进行计算,并将计算结果与实验结果对比,分别如表5 和表6 所列.并由表5 和表6 中的数据按比例绘出相应的实验与模型的矩移比较图和塞曼能移比较图,具体见图3 和图4.

表5 87Rbn 和85Rbn 等数簇矩移模型与实验结果对比Table 5. Comparison of experiment values and calculated values of magnetic moment shift interval of 87Rbn and 85Rbn.

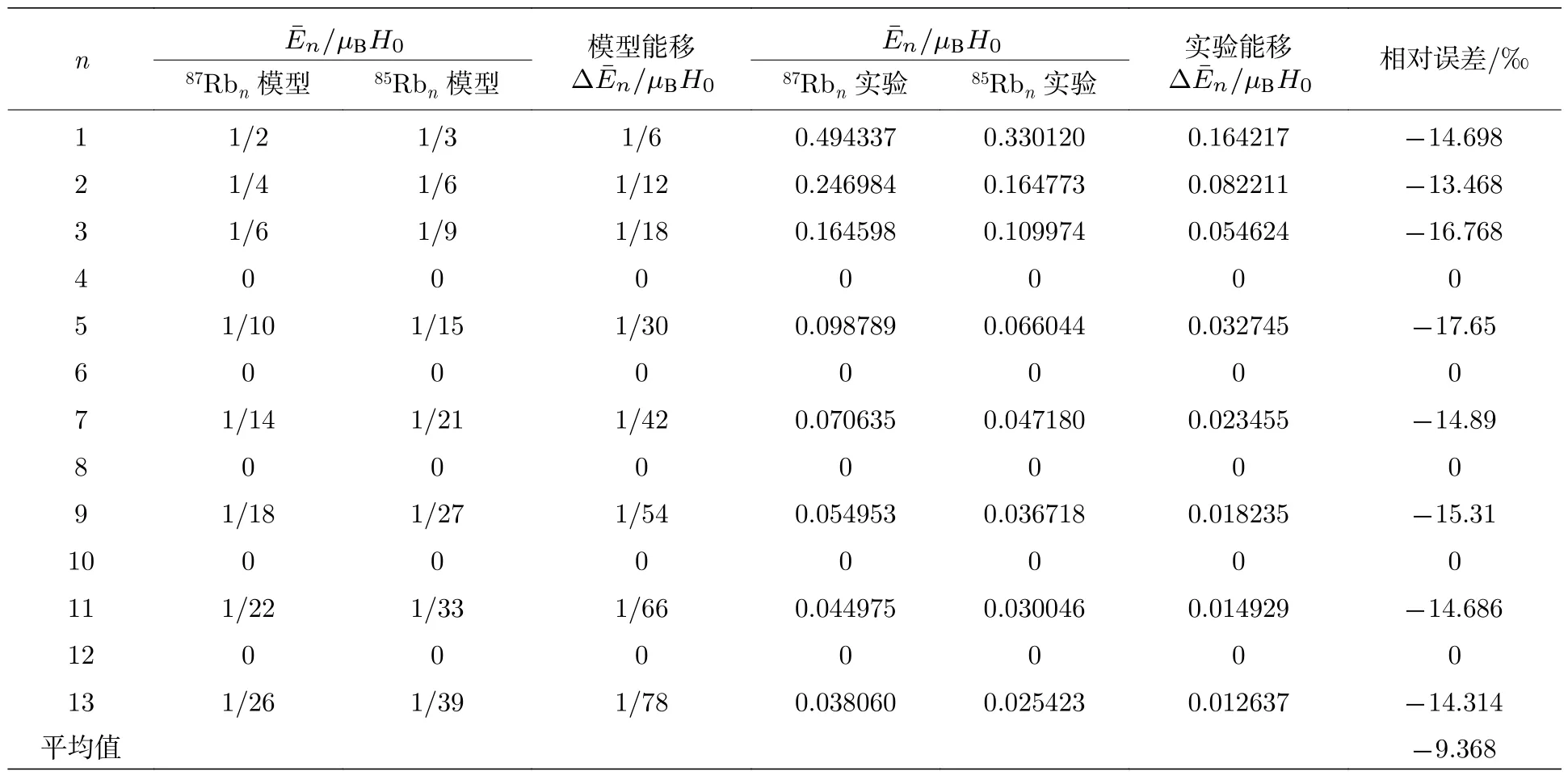
表6 87Rbn 和85Rbn 等数簇塞曼能移实验与模型结果比较Table 6. Comparison of experiment values and calculated values of Zeeman energy level shiift interval of 87Rbn and 85Rbn.

图3 等数簇矩移随n 变化的模型值与实验值比较图(实验值用虚线,模型值用实线)Fig.3.Comparison of calculated values and experimental values of magnetic moment shift of equal number cluster with n (dashed lines for experimental value,full lines for model value).

图4 等数簇超精细结构塞曼能移随n 变化的模型值与实验值比较图(实验值用虚线,模型值用实线)Fig.4.Comparison of calculated values and experimental values of Zeeman energy shift of equal-number hyperfine structures with n(dashed lines for experimental value,full lines for model value).

4.4 5s 单电子壳层能级结构推算

实验中测量的每个簇的塞曼能级间隔均是每个簇粒子的薛定谔方程的一个能量特解[22].将实测的共振离解光谱中的奇偶交替变换特性和随n的递增总的塞曼能级间隔越来越弱的趋势以及n=2的磁矩反常特性与团簇的5s 电子结构相联系起来,可认为电子结构确与磁矩性质密切相关,由此形成了塞曼能级间隔奇偶交替变换且随n的递增越来越小越来越弱的总趋势.直到很大的团簇比如n>21 以后的塞曼能级间隔耗尽而未能观测出来.

扩展研究范围,将(7)–(10)式中的n由n=1,2,···,13 扩展到n=1–92 个原子的簇分子,并将相邻原子簇的塞曼能级间隔差值与铷簇5s 电子壳层结构主要秩序n=2,8,20,40,58 和92 等关联起来,认为壳层结构是由不同能级之间的塞曼大能隙决定的,计算出5s 电子壳层结构,即利用87Rbn,85Rbn塞曼能级间隔公式,计算5s 电子壳层的能隙,87Rbn奇数簇和n=2 的塞曼能级间隔为其余偶数均为0;85Rbn奇数簇和n=2 的,其余偶数均为0.然后计算出相邻簇之间的塞曼能级间隔差值,并定义为△N,这里参考了文献[11]的相关规定,再定义△(N+1),认为n是满壳层原子个数,△(N+1)定义是n后的下一个原子就开始填充一个新的轨道的能级间隔差值.如图5(a)和图5(b)所示,黑色曲线呈现了△N随n的变化曲线,绿色曲线标记了△(N+1)－△N随n的变化大小及趋势和位置,即图5(a)和图5(b)给出了铷的两个同位素原子簇5s 电子壳层能级结构图.

图5 (a) 87Rbn 5s 电子壳层能级结构;(b) 85Rbn 5s 电子壳层能级结构Fig.5. (a) 5s electron shell level structure of 87Rbn;(b) 5s electron shell level structure of 85Rbn.

再将图5(a)和图5(b)与文献[11]的图1 进行对比,可以看出,由塞曼能计算出的铷簇5s 电子的壳层趋势特征及峰值秩序的节奏与钠簇的独立离域原子的3s 电子被束缚在一个球对称势阱中,用薛定谔方程能量特征值计算出来的总结合能的单电子壳结构的趋势特征及峰值秩序节奏相似[11],这表明碱簇不论是总塞曼能还是总结合能均代表着每个簇粒子相应分子态一种形式的能量值,具有协调一致性.由图5(a)和图5(b)还可以看出,随着n的增大相邻簇之间的塞曼能级间隔差值呈现出奇偶交替正负变换特性并持续而缓慢地下降,由此看出Rb 簇中离子-离子静电能和簇离子实对s 电子的费米作用能对总塞曼能的贡献对n是平滑函数,与期望一致,因此电子与电子之间作用能的不连续性也应该保持在团簇的总塞曼能中.由此证明铷簇和钠簇一样,同样具有巨原子能级结构模型特征[12],使图5(a)和图5(b)的5s 单电子壳层结构与钠簇的3s 电子壳层结构图1[11]相辅相承.n=2时的反常磁矩也导致了n=2 与n=3 之间的反常塞曼能级间隔差值为负,由此证明,铷团簇光谱中特殊数的峰或阶跃是由电子性质和分子结构特性引起的.

另外,由图5(a)和图5(b)可明显看到,虽然87Rbn与85Rbn5s 单电子壳层结构主要秩序与步调均严格一致,但大小不同,量值均有3/2 的比值关系,表现出显著的同位素效应.

5 显著性同位素效应原因讨论

5.1 数据分离度

两个同位素单原子的磁矩μB/2 和μB/3 之间相差33.33%,塞曼能级间隔也相差33.33%,两个原子产生如此巨大的反常磁矩差异与塞曼能级间隔差异的原因与各自的核自旋相关,铷核自旋大小和性质取决于处于单粒子态核能级的价质子能级,铷同位素87,85Rb 的第37 个核质子分别处在铷核纲图的2P3/2和1f5/2能级上,文献[23]指出,这两个能级之间存在巨大的能级分离度,与两同位素的核素的中子数N=48,50 接近核壳层闭合面的附近直接相关.

5.2 光谱中心宽度和展宽与核变形

对共振离解光谱的中心宽度、主要宽度、展宽进行标记,如图6(a)和图6(b)所示.将光谱中心频率处的中心宽度称为CC,将光谱的主要宽度部分称为MC、全部展宽称为BC[14],实验发现不论是哪个簇粒子的共振频率中心位置的宽度CC 几乎不随磁场变化,这是由未偶电子的顺磁性而定.而主要区域MC 的幅度会随共振磁场由小到大有50%减小,将随磁场变化的中心频率处的峰值和尾部连带一起的有50%以内缩放的区域称为光谱的主要部分MC,它可以用未偶的顺磁电子自旋的局部场的影响来解释,由未偶价电子的弛豫时间T2长短不同的位点叠加形成.主要区域MC,因变数复杂,此处不列详细数据.

图6 (a),(b) 87Rbn,85Rbn 同位素原子簇的相对频移图Fig.6.(a),(b) Diagrams of relative frequency shift of equal-number cluster 87Rbn,85Rbn.

观察到簇光谱还包括更宽的和弱的成分,称之为“广泛成分宽度BC”,这次记录了328 K 温度的共振光谱宽度数据,证实BC 宽度确与场和温度无关[14],BC 可能是簇(实)核四极效应导致CC 核卫星分裂的结果.

本文仅对n=1,5,7,9 的同位素等数簇光谱中心区域CC、全部展宽BC 在磁场强度2.376257–4.752514 G 范围内进行了全面的数据测量,对于n取其他值的情况,由于87Rb3,85Rb2光谱重叠和n=11,13 时信号太弱不易测量频移,此处不再详述.在磁场测量范围内,n=1,5,7,9 的CC 和广泛成分平均宽度BC 见表7.

表7 实验测量 87Rbn,85Rbn 光谱中心频率宽度与广泛成分平均宽度BCTable 7. Spectral center frequency width CC and average width BC of 87Rbn,85Rbn measured by experiments.

从表7 可以看出,n=7 变形最反常,CC87/CC85=0.46,BC87/BC85=1.57,推测n=7 在其中是最接近5s 单电子闭合壳层n=8 的缘故;同时也可观察到n=1 时87Rb,85Rb 两同位素原子中心频率宽度CC 差异近20%,核变形使二者的BC 宽度比为1.59,差异明显反常,看似两个原子有同样的电子结构,而实际上两同位素的电子能级结构有很大区别,n=5,9 时的CC 与BC 情况与n=1 的87Rb,85Rb 反常差异有类同之处.实验结果也证明87Rbn和85Rbn的电子能级结构很不同,因为两同位素的ns 电子之间不能形成平等的共价键,长期多年的实验中始终未能检测到共价形式的(87Rb85Rb)n交叉簇的存在,而只能在混合同位素饱和蒸汽中检测到纯单一同位素原子簇的存在.

由CC 和BC 数据规律性表明87Rbn,85Rbn两同位素等数簇的光谱形态变形显著,是由同位素簇的簇分子实的巨大变形而导致的,簇分子实的变形是每一个原子核变形造成的,由此间接证实了85Rb,87Rb 原子的价质子与中子数48 或50 的核素耦合结构处于核壳层闭合面附近,因为只有处于核壳层闭合面的两个同位素具有的显著性核变形差异,很容易被辨认出来[23].

6 结论

1)通过共振离解技术成功量化研究了87Rbn,85Rbn两系列原子簇的同位素效应.87Rbn,85Rbn等数簇的磁矩量化表达式分别为且均与其簇分子合角动量数值成反比,偶数簇除n=2 外的原子簇磁矩均为0;等数簇量化矩移表达式为量化塞曼能移表达式为

2)实测结果与模型计算之间的良好对应关系,证实铷簇从磁矩和塞曼能级间隔的数值到5s 单电子壳结构的秩序均与巨原子模型自洽,其共振离解光谱奇偶交替特性与特殊数的峰或阶跃均是由5s 电子内在性质及簇分子结构引起的;87Rbn与85Rbn两系列原子簇5s 单电子壳结构的步调严格一致,但能隙大小不同,量值均约有3/2 的比值关系.

3)显著的同位素效应及等数簇光谱宽度与展宽差异的反常均是85Rb,87Rb 两个同位素的核素结构处于核壳层闭合面附近的证明.