机器学习结合固溶强化模型预测高熵合金硬度*

张逸凡 任卫† 王伟丽 丁书剑 李楠 常亮 周倩

1) (西安邮电大学理学院,西安 710121)

2) (西北工业大学物理科学与技术学院,西安 710072)

第一性原理、热力学模拟等传统的材料计算方法在高熵合金的设计中多用于合金相的预测,同时会耗费巨大的计算资源.本文以性能为导向,选用机器学习的算法建立了一个高熵合金硬度预测模型,并将机器学习与固溶体强化的物理模型相结合,使用遗传算法筛选出最具有代表性的3 个特征参数,利用这3 个特征构建的随机森林模型,其R2 达到了0.9416,对高熵合金的硬度取得了较好的预测效果.本文选用的机器学习算法和3 个材料特征在固溶体强化性质方面也有一定的预测效果.针对随机森林可解释性较差的问题,本文还利用SHAP 可解释机器学习方法挖掘了机器学习模型的内在推理逻辑.

1 引言

高熵合金(HEA)是由4 种或4 种以上金属元素按照等原子百分比或近似等原子百分比合成的合金材料[1].高熵合金的各主元金属元素间发生复杂的相互作用而产生著名的四大效应[2](高熵效应、晶格畸变、迟滞扩散效应和“鸡尾酒”效应),从而可能会使材料表现出极其优异的性能(例如耐腐蚀性、高温热稳定性、力学性能、磁性等)[3-5].然而,由于高熵合金含有多种主元金属,其成分的组合空间包含了1078种组合方式[6],这就导致精确快速地筛选出具有优异目标性能的高熵合金成分是非常困难的.

第一性原理、热力学仿真等[7-9]传统的材料设计方法虽然能够加速新材料的发现,但这些方法很难灵活地根据目标性能构建模型,而且这些方法占用了很大的计算资源,计算成本很高,然而预测精度一般.随着人工智能的快速发展,机器学习(ML)逐渐开始应用到材料科学中[10-13].与传统材料计算方法相比,机器学习通过大量的数据训练,建立输入特征与目标性质之间的映射关系.由于材料学科在漫长的发展进程中积累了大量的研究数据,机器学习可以从这些数据中挖掘数据所蕴含的信息,从而快速、精准地预测出材料的性质.Khakurel 等[14]选取了梯度提升算法来评估特征重要性,有效地预测了难熔高熵合金的杨氏模量.Chang 等[15]使用成分加权和密度等材料特征建立了三层人工神经网络(ANN)来预测AlCoCrFeMnNi 体系高熵合金的硬度.Bakr 等[16]利用ANN 预测了高熵合金的硬度,最终模型的决定系数达到了0.88.上述研究使用的模型虽然都具有一定的预测能力,却难以兼顾模型的可解释性和预测精度的问题.Li 和Guo[17]采用前向和后向特征选择得到的材料特征建立了一个支持向量机模型(SVM)用于预测高熵合金的合金相,准确率超过了90%.Xiong 等[18]利用前向特征选择法筛选的特征预测了合金相及相关力学性能.Lee 等[19]使用皮尔逊相关系数法(PCC)筛选特征并将神经网络算法集成获得了一个合金相分类器.Sun 等[13]利用XGBoost 算法拟合相图计算辅助构建的Ti-Zr-Nb-Ta 高熵合金硬度数据集,通过特征重要性排名等特征选择方法,揭示了预测该体系合金硬度的两个最重要的特征为Ta 含量和熔点,同时模型获得了87.6%的预测准确率.Wen等[20]在模型构建的特征选择时利用皮尔逊相关系数法去除冗余特征,随后通过将特征穷举完成特征选择,并使得支持向量机构建的硬度预测模型的精度有所提高.最后联合支持向量机和效用函数成功搜索到了候选的高硬度HEA.Li 等[21]将Stacking集成学习算法用于硬度预测,成功降低了HEA 硬度预测模型的预测误差.然而,上述研究使用的特征选择方法多为与模型无关的方法或贪心算法,这些方法只覆盖了很少部分的特征组合,甚至忽略了模型与特征间的关系,这导致了建模时所使用特征组的质量相对较低.此外,在特征选择时上述研究大多针对单一特征集进行筛选,在实际的特征选择过程中会忽略大量特征集之外的特征,造成筛选出的特征仅有部分代表性.而且由于高熵合金复杂的多主元结构及其形成机理,构建一个完全包含所有影响硬度因素的特征集很困难.而且上述研究筛选的特征都只针对某种单一HEA 体系的性质进行预测是有效的,而难以对其他HEA 体系或HEA 性质的性质进行预测.此时,构建一个科学合理的特征选择框架是至关重要的.这将有利于构建一个适用于预测多种相关HEA 性质的建模特征集,进而可以从机理上反映出HEA 不同性能之间的关系.因而,在使用机器学习预测HEA 性质的领域(尤其是对HEA 硬度的预测),特征集的构建和特征选择的方法仍然具有改进空间.此外,由于机器学习多为黑盒模型,所以预测模型的可解释性也至关重要,这决定了是否可以进一步挖掘HEA 形成的内部机制和预测模型的进一步优化.

本文首先建立了一个包含19 个特征的高熵合金硬度数据集,并利用该数据集选取建立模型的机器学习算法.经过测试多种特征选择算法,发现由遗传算法筛选出的候选特征质量较好.同时,为了克服候选特征迁移性差的问题,结合传统固溶体强化(SSS)物理模型,对候选特征进行进一步筛选和优化.最后,采用了SHAP 可解释机器学习方法[22]挖掘了输入特征对高熵合金硬度的影响机理.

2 建模条件

2.1 数据集与候选材料特征参数

本文选用文献[20,21]使用的高熵合金材料硬度数据集,该数据集包含了Al,Co,Cr,Cu,Fe 和Ni 六元高熵合金硬度样本,计205 条数据.由于铸态条件下形成的相是稳定的,所以合金的硬度数据均在铸态条件下测量[23].数据集包含了一些数值异常的数据.分析认为,这些异常数据并不是因为测量误差导致的,它们可能是由HEA 固有的性质引起的数据差异,应予以保留.

为了尽可能将与硬度相关的候选特征纳入特征集,我们考察了曾广泛用于HEA 性能预测的多个材料特征参数.其中原子尺寸错配和模量错配对HEA 的硬度有巨大的贡献[20].基于此,首先将原子半径误配(δr)、原子堆叠失配因子 (γ)、杨氏模量(E)、剪切模量(G)、剪切模量误配(δG)、晶格畸变能(μ)、Peierls-Nabarro 因子(F)、强化模型中的能量项(A)等与原子尺寸和模量相关的特征参数加入特征集中.其次,高熵合金的相与其硬度有着很强的关联性.Wang 等[24]发现功函数的六次方(w6)与合金的屈服强度呈线性关系.Guo[25]回顾了根据经典Hume Rothery 规则选取的γ,Ω,Λ等经验参数区分各类相的研究,讨论了混合焓(△Hmix)、混合熵(△Smix)、吉布斯自由能(△Gmix)、平均熔点(Tm)、电负差(△χ)和价电子浓度(VEC)等参数对高熵合金相形成的影响.这些参数也很重要,需要被加入特征集.此外,巡回电子浓度(e/a)和内聚能(Ec)等与电子键合强度和电学性质有关的相稳定性参数也被加入特征集中.由于HEA 的硬度对组织变化很敏感,还选取了一些与HEA 力学性能相关的描述因子.这样就得到了一个含有19 个材料特征的HEA 材料候选特征数据集.相关参数及计算公式如表1 所列,其中rmin ,rmax 代表HEA 中最小和最大原子半径;ci代表各元素摩尔比;r表示原子平均半径;R为气体常数表示第i和第j个元素之间的混合焓.

表1 与高熵合金硬度相关的 19 个经验特征参数及其计算公式Table 1. 19 empirical feature parameters related to the hardness of high entropy alloys and their calculation formulae.

2.2 机器学习算法的选择

由于选择恰当的ML 算法对于精准高效拟合HEA 硬度数据具有重要的作用,我们对适用于不同数据类型的ML 算法及其特点进行了必要筛查.

集成学习算法是一种重要的ML 算法.早期,因为其缺少可解释性而仅获有限的应用[20,21,26].随着可解释ML 的发展,使用集成学习结合可解释ML 的分析预测方法可以克服传统ML 算法泛化性不足,还可以兼顾模型的可解释性,因而能挖掘大量有用信息.SVM 和ANN 分别由于其核函数、支持向量机制和反向传播、激活函数机制使其具有强大的非线性映射能力,因而广泛地应用在各类研究场景中.此外,基于线性回归的ML 算法由于其强大的可解释性,也被广泛用于建模中.Grinsztajn等[27]发现基于树的模型(包括随机森林(RF)和XGBoost 等算法) 在利用表格数据进行预测方面超过了深度残差网络等其他深度学习模型.由于本文使用的HEA 硬度数据集样本规模小,数据不均匀,基于树的模型可能更适合该数据集.虽然上述模型都可以确立特征与目标值之间的隐式关系,不同的ML 模型对数据采用不同的处理手段,所获得的模型可解释性是不同的,在建模中要根据不同的目标值选取合适的ML 模型.本文在建模中使用了Python 的sklearn,pandas,numpy 等常用数据分析库.

最后,在利用HEA 数据集构建ML 模型之前,还要考虑如何降低模型过拟合或欠拟合所带来的风险.传统的按固定比例划分数据集来评价模型精度的方法会因为数据不平衡而导致模型泛化性差.所以本文在建立ML 模型过程中始终将交叉验证的方法应用于ML 模型选择、ML 参数调优、ML预测结果评估等各个阶段,从而保证了建模结果的科学性和可信性.各阶段使用的评价依据为均方误差

3 建模和结果

3.1 基准机器学习算法

为选出最合适的基准算法,本文使用了具有优异外推能力的线性算法(Ridge 和Lasso),SVM,具有单隐藏层的ANN,性能优异但外推能力较差的集成学习算法(如基于Bagging 的代表算法RF和基于Boosting[28]的代表算法XGBoost).首先,将前述19 个候选材料特征作为输入参数,将HEA硬度值作为输出值,依次对上述ML 算法进行训练.为确保发挥出各个ML 算法的特点和优势,在对ML 算法进行训练时,将网格搜索法和十折交叉验证法(10-fold)相结合搜索使模型RMSE 最小的超参数.经过寻优搜索和交叉验证,在SVM 的3 种核函数中选择了非线性映射能力最好的高斯核函数(SVM-rbf).ANN 在使用Adam 作为反向传播优化器和线性修正函数作为激活函数时取得了最优的结果.机器学习模型搜索的超参数结果如表2所列,所有超参数的相关解释详见sklearn.此外,为了增强模型的物理可解释性,并没有对特征集进行数据标准化或数据降维等数据预处理操作[29,30].

表2 不同机器学习模型搜索的超参数结果Table 2. Hyperparametric search results for different machine learning models.

将搜索的超参数应用到ML 算法上,通过10-fold 验证的方法评估了前述ML 算法的RMSE 和R2,结果如图1 所示.

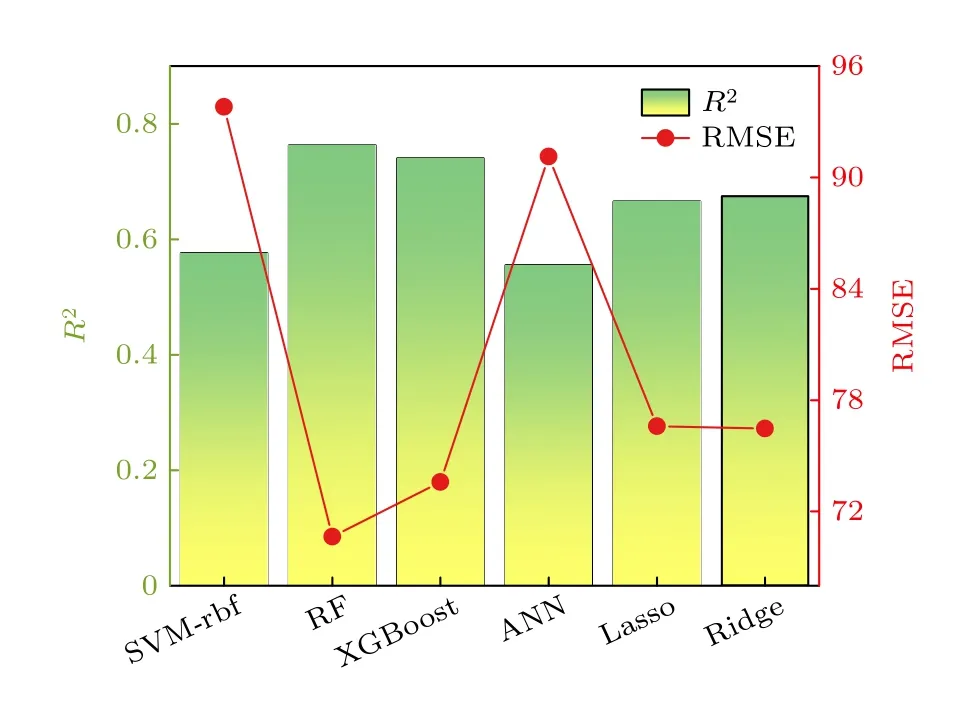
图1 6 种机器学习算法对数据集的拟合结果Fig.1.Fitting results of six machine learning algorithms to the dataset.

从图1 可以看出,RF 不仅取得了最高的R2,并且有着最小的RMSE,这表明了RF 在该数据集上具有最佳拟合效果.所以将RF 作为接下来进行特征选择和模型建立的基准算法.

3.2 优化特征组筛选及特征解释

从候选特征集筛选出优化的特征组合,经过模型训练,能够使数据拟合的误差达到最小.由于不同数据集的样本分布不同,所以在对该数据集先验知识不足的情况下,需要利用多种与ML 算法相关的特征选择方法主动选择适合该ML 算法的特征组合,从而更好地解释目标属性.本文分别使用了包裹法和嵌入法进行特征筛选.包裹法通过使用特征搜索策略修改特征组合,以此来选择出优化特征子集.该方法主要包括遗传算法(GA)、序列前向选择(SFS)、序列后向选择(SBS)、递归特征消除(RFE)等方法.嵌入法利用前述RF 算法学习器对特征重要性进行评估,依次从特征集中剔除不重要特征,以此筛选出表现最好的特征组.其中,GA 是一种通过模拟自然选择、遗传和变异等生物进化过程来寻找最优解的最优化算法.GA 通过初始化种群、评估适应度、选择、交叉和变异等步骤来寻找最优化问题的最优解.具体地,将GA 运用到特征选择时,本文将随机森林模型在十折交叉验证法下的RMSE 作为适应度用于评估每个特征集合的优良程度;初始化种群即为所有可能的特征集合的集合;在执行选择操作时将优秀的特征集合复制到下一代来保留优秀的基因,同时引入新的变异来增加种群的多样性;在执行交叉操作时,将两个特征集合的某些部分进行交换,以产生新的特征集合.交叉操作可以促进基因的流动和交换,从而增加种群的多样性;在执行变异操作时,通过添加或删除某些特征来增加特征集合的随机性,以增加种群的多样性.在执行GA 时使用了python 中的genetic_selection 库,将最小化随机森林模型在十折交叉验证法下的RMSE 为目标,利用GA 对特征集进行全局特征搜索,最后通过执行上述优化步骤筛选出最优的特征组.对于RFE,SFS,SBS 以及基于RF的包裹法,利用python 中的sklearn 库,测试了在各个特征选择方法下保留不同特征数量时的特征选择结果.如图2 所示,对除全局优化算法的GA之外的其他4 种特征选择方法进行测试.在使用不同特征选择算法时,设定保留的特征数量分别为1 到19,选择出不同特征选择算法在保留不同特征数量下的特征集.随后,通过对比各个特征选择算法在保留不同特征数量下的RMSE,选出各个特征选择算法下的最优特征集.如表3 所列,RFE和RF 分别筛选出了含有13 个特征的优化特征组,虽然它们使用了较多的材料特征而对HEA 硬度预测的表现则较差.SBS 和SFS 算法筛选出了含有7 个特征的优化特征组,其RMSE 约为67,预测表现略高于RFE 和RF.而GA 筛选出了含有8 个特征的优化特征组,其RMSE 仅为64.09.预测表现明显优于其他特征选择算法.这可能是因为GA 是一个全局搜索算法,其遍历的特征组合更加全面.因而本文使用GA 进行特征选择.

图2 SBS,SFS,RF,RFE 算法在不同特征数下选择的最佳特征的RMSE,曲线中的星号代表了当前特征选择方法选择的最优特征组所包含的特征数Fig.2.Different number of features selected by SBS,SFS,RF,RFE algorithm vs.their RMSE performances under 10 fold.The asterisks in the curves represent the number of features contained in the optimal feature group selected by the current feature selection method.

表3 不同特征选择方法筛选的优化特征组及RMSE 值Table 3. Optimized feature sets screened by different feature selection algorithms and their RMSE values.

为了克服集成学习可解释性差的问题,采用Lundberg 和Lee[31]提出的沙普利加和解释(SHAP)方法.SHAP 是一种解释ML 模型输出的博弈论方法,通过计算各个特征对预测结果的边际贡献,完成对黑盒模型局部或全局的分析.如图3 所示,利用SHAP 方法解释GA 选择的优化特征组特征对HEA 硬度的影响.根据文献[25],VEC ,∆χ等材料特征参数能影响HEA 形成FCC 相和BCC 相的稳定性: 当 VEC<6.87 时HEA 倾向于生成BCC相,当 VEC>8 时倾向于生成FCC 相,当6.871.175 时,HEA 更倾向于生成金属间化合物(IM).IM 相对于固溶相(SSP)来说,其硬度更大,脆性也更大.同样地,根据Hume-Rothery 准则,∆χ较大时,HEA 体系中具有高电正性的元素原子容易失去核外电子,高电负性元素原子则容易得电子,故高电负性元素吸引共用电子的能力也会变大,此时HEA 更易形成IM,从而提高HEA 硬度.Yang 和Zhang[36]提出的热力学参数Ω反映了熵和焓之间的竞争.考虑△Hmix和△Smix等热力学参数对HEA 相形成的影响,其中△Hmix阻碍固溶体的形成,△Smix促使形成固溶体,当Ω参数较小时,说明△Hmix在HEA 体系固溶体形成中处于主导地位,此时不易形成固溶体,硬度较大的IM 将优先形成;反之,当Ω参数较大时,△Smix在HEA体系固溶体形成中处于主导地位,容易生成固溶体.经过SHAP 方法的分析,GA 选出的优化特征组所包含的特征参数 [γ,∆χ,δG] 在SHAP 排序中靠前,表明这些特征在ML 建模中很重要.同时[δG,E] 参数也与模量相关,而模量参数在传统物理计算模型中占据了非常重要的部分.这些结果表明通过GA 筛选出的材料特征具有重要物理意义,对于进一步改进力学性能预测模型具有很好的指导作用.

图3 遗传算法所选优化特征组8 种特征的SHAP 分析,8 种特征由上到下重要性依次降低,各个散点根据SHAP值的正负反映了该特征的大小对当前样本点硬度的促进或削弱作用Fig.3.SHAP analysis of the eight features of the optimized feature set selected by the genetic algorithm.The eight features decrease in importance from top to bottom.Each scatter reflects the promoting or weakening effect of the size of the feature on the hardness of the current sample point according to the positive or negative SHAP value.

3.3 基于固溶强化理论优化输入特征

为分析GA 所选择的8 个特征间是否存在冗余特征,明确是否需要进一步优化特征集,计算了各个特征以及HEA 硬度之间的PCC.图4(a)的子图是使用基准算法RF 评估的各个特征的重要性排序,其中 VEC ,F,δG,∆χ等参数与PCC 得到的特征和硬度间的相关性基本一致.将|PCC|>0.8 的特征视为高相关特征.如图4(a)所示,[γ,F],[∆χ,F],[ VEC,e/a,δG] 这些特征组合相关性相对较高.对于这些特征组合,不能简单通过评估特征重要性来删除不重要特征,因为这样做可能忽略了各个特征对HEA 硬度的协同促进作用.此外,PCC 是基于变量之间的线性相关性来衡量它们之间的关联程度.然而,如果特征之间存在非线性关系,PCC 可能无法准确反映它们之间的相关性.HEA 复杂的形成机制蕴含着复杂的非线性关系.利用PCC 筛选特征,可能会忽略这些关系,从而漏选重要特征.其次,PCC 仅考虑特征之间的两两关系,并不能全面捕捉多个特征之间的复杂关系.在复杂的HEA 材料数据中,多个特征之间可能存在更高阶的相互作用或非线性关系,这些关系无法通过皮尔逊相关系数来准确表示.最后,PCC 只考虑了特征之间的相关性,而忽略了特征与目标变量之间的关联性,这可能会删除一些对于目标值预测比较重要的特征.图4(b)对该特征组进行主成分分析,发现在8 个特征中,只需提取3 个主成分即可保留特征集所有的信息.这为我们选取更加优化的输入特征提供了一个思路.同时,这也意味着特征集仍具有改进的空间.为了提升模型精度,令模型更具可解释性,需要依据当前特征选择的结果,进一步扩充特征集,选择更加具有代表性的特征,进而优化建模特征组.

图4 (a)遗传算法所选特征的PCC 热图,子图为遗传算法所选特征的RF 重要性评估排序;(b)主成分分析法计算优化特征组 [γ,∆χ,VEC,F,Ω,e/a,E,δG] 不同主成分数的累计方差贡献率;(c)新构建的特征集进行GA 特征选择的迭代过程,子图为GA 选择特征的SHAP 重要性排序Fig.4.(a) PCC heat map of the features selected by the genetic algorithm,with subplots for the RF importance assessment ranking of the features selected by the genetic algorithm;(b) the cumulative variance contribution of different principal component scores of the optimized feature set[γ,∆χ,VEC,F,Ω,e/a,E,δG]calculated by principal component analysis;(c) iterative process of GA feature selection for the newly constructed feature set,and the subplot is the SHAP importance ranking of the GA selected features.

HEAs 的强化机制主要由SSS 导致,其中屈服强度和维氏硬度正相关,且屈服强度约为维氏硬度的9.81/3 倍,所以SSS 对HEA 维氏硬度的提升很重要.

一般认为,HEAs 的SSS 主要由溶质原子引起的晶格畸变和滑动位错引起,其中金属元素的尺寸错配和模量错配引起的晶格畸变在合金强化中占据重要地位.经典的Labusch 模型[37]体现了尺寸误配和模量误配对SSS 的影响.传统的SSS 数学模型,大多是基于Labusch 模型进行改进.Thirathipviwat 等[38]发现高晶格畸变引起显微硬度的变化与 δr正相关;Ma 和Wu[39]也发现 δr有利于导致位错线形成波浪形构型,这为HEA 提供了显著的SSS效果.Toda-Caraballo 和Rivera-Díaz-del-Castillo[40]利用Gypen 模型将Labusch 模型从二元合金推广到稀释的多组分合金,通过计算原子间距变化,量化各组分引起的晶格畸变对SSS 的贡献来估计合金的SSS 程度.所以原子尺寸失配与模量失配对SSS 有着重要影响.Toda Caraballo 提出的SSS模型等式可表示为[34]

其中ξ为SSS 模型的结构因子,BCC 相为4,FCC相为1;δ为模型的SSS 强化因子,与原子尺寸误配相关; ∆σSSS为量化固溶强化程度的参数;Z为固溶强化因子.

基于上述理论,我们发现在GA 所选的8 个特征中,HEA 的硬度与模量,原子半径和电负差的误配有关.这也暗示了此类特征与HEA 硬度增强有关.以此为基础,将3.2 节中筛选出的E,G以及体积模量(K)作为原始数据,通过(2)–(6) 式计算5 个与误配相关的特征:

其中d分别代表杨氏模量、剪切模量、体积模量、原子半径和电负性等参数,ci代表HEA 各元素的摩尔比,di代表HEA 各元素的参数αi值.由于γ参数与金属原子尺寸误配相关,所以将原子半径同样利用(2)–(6)式的方法扩充尺寸误配特征.将重新计算的特征与3.2 节中筛选的特征组[γ,∆χ,VEC,F,Ω,e/a,E,δG]整合到一起,组成了含有35 个特征参数的扩充特征集,然后通过GA 重新进行特征选择.

如图4(c)所示,GA 在迭代到第30 代时,收敛到最优解,此时搜寻到的简版优化特征组为[VEC,G,M.E].相对于GA 最初筛选的包含8 个特征的优化特征组,简版优化特征组仅用3 个参数来构建ML 模型,并且由于使用G和M.E 这两个特征取代其他大量的特征,极大减少了冗余特征,降低了模型复杂度.

在对ML 模型进行评估的时候,不仅要评估模型泛化性,还要评估模型的外推能力.10-fold 是将数据集平均分为10 份,评估ML 算法在其中9 份数据集上的训练结果是否可以迁移到剩余的1 份数据集上.该方法可以用来评估ML 模型的泛化能力.由于采用的材料硬度数据具有稀疏性,可能由于数据集划分不当,导致模型训练信息遗漏,使模型在不同测试集上的表现差距较大,导致模型缺乏外推能力.因而可以采用留一交叉验证(LOOCV)评价模型的外推能力.具体作法是分别将简版优化特征组和优化特征组作为RF 的输入,利用贝叶斯优化方法优化RF 超参数提高模型预测性能.如图5 所示,虽然简版优化特征组去除了多数输入特征参数,但是模型在10-fold 和LOOCV 情况下的RMSE 和R2相较于优化特征组仍然有一定程度的进步.为了进一步分析2.1 节所述异常值对本文建模的影响,使用了孤立森林算法对数据集进行异常值检测.孤立森林算法是一种无监督的离群点检测算法.该算法的优点包括能够快速准确地识别异常值点,并且内存使用率低.此外,由于该算法建立在基于树的结构上,因此实现简单,是异常检测的有效工具.如图6(c)所示,使用孤立森林对数据集的样本进行评分,得分小于零则视为离群点,最后发现了11 个离群点.将这11 个离群点从数据集剔除后,分别使用LOOCV 和10-fold 评估模型的R2和RMSE.如图6(a)和图6(b)以及图5(c)和图5(d)所示,去除异常值后的R2和RMSE 相较于去除前,精度有所下降.这可能是由于我们在所使用的数据集均来源于真实世界,并且通过科学合理的方法测量,所以异常值点是由测量误差导致的概率比较低.异常值点在真实世界是客观存在的,所以一些异常点的情况必须被考虑到其中,这可以建立模型和真实世界的联系.同时,如果在预测新样本时,该样本恰好与以前剔除的异常值点类型相同,此时预测偏差可能会急剧上升.所以在本文中将会保留异常值.另一方面,由于LOOCV 对异常值点的存在非常敏感,所以LOOCV 的评估结果对于模型离群点的实际影响可以作为参考.如图6(b)和图5(d)所示,在LOOCV 的测试下,并没有出现很明显的离群点.这也证明了少量的异常值点对建模的影响并不大.

图5 (a),(c) 在十折交叉验证下的模型拟合结果以及(b),(d)在LOCOCV 下的模型拟合结果,其中(a),(b) 优化特征组[γ,∆χ,VEC,F,Ω,e/a,E,δG] 作为RF 输入特征;(c),(d)简版优化特征组 [VEC,G,M.E] 作为RF 输入特征Fig.5.(a),(c) Model fit results under 10-fold cross-validation and (b),(d) model fit results under LOCOCV: (a),(b) Optimized feature set [γ,∆χ,VEC,F,Ω,e/a,E,δG] as RF input features;(c),(d) the short version of the optimized feature set[VEC,G,M.E]as RF input features.

图6 数据集去除异常值后的拟合图 (a)使用了10-fold评估;(b) 使用了LOOCV 评估;(c) 主图为异常值得分结果,Scores <0 视为离群点;利用孤立森林对205 个高熵合金样本进行异常值检测,子图为利用主成分分析法降维后的异常值检测可视化结果Fig.6.Fitted plots of the dataset after removing outliers:(a) 10-fold is used;(b) LOOCV is used;(c) the outlier score histogram (the orange points being outlier points when scores <0).The outlier detection is carried out for 205 high-entropy alloy samples by using isolated forest.The inset 3D figure shows the visualization results of the outlier detection after the dimensionality reduction by using principal component analysis.

为了进一步探索特征集[VEC,G,M.E]在SSS的应用,对SSS 物理模型进行改进.首先经验参数VEC 与ξ的作用类似,都能区分具有FCC 和BCC结构固溶体相的HEA.但ξ参数划分不同相的边界更加清晰.Wen 等[34]使用ξ代替VEC 训练ML模型,获得了更好的SSS 预测结果.针对Toda-Caraballo 和Rivera-Díaz-del-Castillo[40]提出的SSS 物理模型,将特征集[VEC,G,M.E]中的VEC 替换为ξ,得到了该SSS 模型的另外一种表现形式:

为了验证(7)式的准确性,采用文献[34]收集的162 条铸态HEA 的SSS 贡献( ∆σSSC)数据集,该数据集中所包含的金属元素不仅有3d 过渡金属元素(Co,Cr,Cu,Fe,Ni,Mn,Ti,V),还包含Zr,Hf,Mo,Nb,Ta,W,Al 等难熔金属元素.为了更好地估计SSS 对HEA 硬度的贡献,该数据集中只保留了BCC 和FCC 的单相固溶体数据,这样处理可以削弱除SSS 外的其他强化效果的干扰.如图7所示,将[ξ,G,M.E ]作为RF 算法输入,∆σSSC作为输出,经过贝叶斯优化方法对RF 进行超参数优化,最终在10-fold 的情况下RMSE 和R2分别为542.3691 和0.8811.

图7 以[ ξ,G,M.E ]作为RF 输入特征,∆σSSC 作为目标值,在十折交叉验证下的评估结果Fig.7.Evaluation results with [ ξ,G,M.E ] as the RF input features and ∆σSSC as the target values under 10-fold cross-validation.

4 结论

本文首先使用集成学习算法对一个包含19 个候选特征的高熵合金硬度数据集进行训练、测试和评估: 从多种特征选择算法中筛选出遗传算法对19 个候选特征进行筛选,获得包含8 个特征的优化特征组;然后结合两阶段的特征选择方法,利用传统固溶强化模型优化建模特征,最终筛选出包含3 个材料特征的简版最优特征组合 [VEC,G,M.E] ;利用这3 个特征建立的RF 模型使得模型在十折交叉验证法下的R2达到了0.9416,RMSE 达到了52.4594.基于该特征组合建立的模型对于固溶强化的预测也具有一定适应性,在预测固溶体强化的贡献时R2达到了0.8811,这表明该模型对高熵合金力学性质的预测可能也有好的迁移效果.最后,本文使用可解释机器学习挖掘HEA 硬度数据的隐含信息,初步揭示了一些重要材料特征对HEA 硬度的影响机理.