非饱和岩体裂隙中冰层生长试验及单个裂隙壁面上的结霜模型研究
王莉平, 郝哲销, 李 宁, 徐拴海, 王文丽, 朱英豪
(1. 西安理工大学 土木建筑工程学院,陕西 西安 710048; 2. 中国煤炭科工集团西安研究院,陕西 西安 710054)
0 引言
冻胀风化是寒区基岩风化的主要原因[1-2],在冻胀风化作用下,岩体向破碎化方向发展,构成了滑坡、崩塌等地质灾害的物质基础,同时结合搬运等地质作用,长期累积也会引起地形地貌的变化。岩体裂隙中冰夹层的出现及生长是岩体冻胀风化的重要特征及成因,明确寒区岩体裂隙中冰层形成机理,一方面可以为宏观描述岩体冻胀损伤提供理论基础,另一方面有助于理解滑坡崩塌中物质因素的形成过程及相关条件。在此基础上,提出相应工程措施阻止基岩的进一步寒冻风化,降低浅表层地质灾害风险,为寒区工程的设计、施工及运营奠定一定的理论和实践基础。
岩土体中冰层形成和生长的相关机理主要有原位冻胀和分凝冰。原位冻胀是指环境温度降至0 ℃之下时,孔隙或裂隙中的水原地冻结,当条件适宜时,如孔隙或裂隙饱和或接近饱和,且水分难以向周边渗透逃逸时,水变成冰产生约9%的体积膨胀会导致岩土体开裂或既有裂缝扩张[3]。对于现场而言,以上条件相对苛刻,仅在少数情况下会出现,Taber[4-5]也通过试验令人信服地证实了水分的原位冻胀对土体冻胀的影响非常小。分凝冰是指液态水在温度梯度的作用下不断由未冻区迁移至冻结锋面附近,使得冰透镜体或冰层不断生长,呈现出分凝冰层的形态,同时导致了岩土体的开裂或既有裂隙的扩张[3]。Everett[6]基于毛细作用提出的冻胀理论被称为第一冻胀理论,但该理论无法解释冰透镜体的初始成因。Miller[7]基于薄膜水假设提出了土冻结过程中的第二冻胀理论,认为冰透镜体暖端与冻结锋面之间存在一个低含水量、低导水率的区域,并称其为冻结缘。Gilpin[8]建立了水分迁移使得冰透镜体生长的数学模型。O’Neil等[9]建立了一个描述冻胀过程的模型:水分迁移通过冻结缘区域供给活动冰透镜体的生长,直至一个新的冰透镜体启动和开始生长;通过严格耦合冰的饱和度和力的平衡条件,Rempel等[10]基于热分子力建立了冰透镜体的启动和生长模型。受到冻土中分凝冰理论的启发,Walder等[11-12]基于热力学的基本原理,建立了分凝冰生长导致岩石开裂的理论模型。其后Hallet等[13]对Berea 砂岩,Akagawa 等[14]对凝灰岩、Murton等[15-17]对石灰岩,以及吕志涛等[18]对砂岩的相关试验进一步证实了岩石中的分凝冰理论。分凝冰理论很好地解释了北极多年冻土中的裂缝和冰层分布特征及中纬度地区的一些冰期风化特征[3]。分凝冰理论适用于孔隙发育的软~中等硬度的岩石,本质上来说,孔隙发育的岩石与易冻土的结构是非常类似的:孔隙要小到一定程度,可以持水,同时可以提供水分的迁移通道。还有一类是在非饱和土体中,水蒸气迁移至冷端时凝华成霜,在经历复杂的霜冰转化之后形成了冰层,如在寒区地面常常观察到的针状冰现象[19],李强等[20]将覆盖层土体中的含水率过高和结霜现象命名为“锅盖效应”。结合非饱和土水气迁移的物理过程和内在机理,滕继东等[21]将其分为两种情形,第一类“锅盖效应”定义为非饱和土水气的冷凝过程,而第二类“锅盖效应”定义为水气迁移成冰过程。Eigenbrod 等[22]设计冻结试验研究粗粒料中的蒸汽迁移成冰情况,发现在纯净的粗粒土中,由蒸汽迁移造成表层含水率由初始6.6%增大至11.1%,含细粒的砂砾土的表层含水率则由初始8%增大至22%。Guthrie 等[23]的试验结果表明:相比初始41.5%的饱和度,水汽混合迁移导致冻结锋面处含水率大幅提升,达到过饱和状态(115%);张升等[24]研制了非饱和冻土水汽迁移试验仪,对不同初始含水率的试样进行了水汽迁移试验,结果表明初始含水率越大,降温速率越小,则水汽迁移效果越明显。贺佐跃等[25]建立的关于非饱和冻土的耦合模型表明:冻结条件下的气态水迁移主要受温度势而非基质势的作用,粉土和砂土中的气态水迁移是不能忽略的,而黏土中几乎没有气态水迁移。
以上成冰机理均是对于孔隙介质而言,而寒区非饱和裂隙岩体是由裂隙加岩石基质构成,裂隙与可视为孔隙介质的岩石基质性质差异巨大,多数情况下裂隙是水分主要的储存及运移通道,同时由于裂隙多不饱和,其中同时存在着气态迁移和液态迁移,很难直接以上述三种机理解释冰层形成及生长过程。为研究非饱和岩体裂隙中冰层出现及生长情况,作者将两块水泥试块拼接成带有垂直裂隙的模拟裂隙岩体试样,并对此试样进行了暖端补水条件下的单向冻结试验。试验结果表明水分主要以水蒸气形式在岩体裂隙中迁移,并在裂隙壁面的负温区凝华成霜。基于热力学基本原理,建立了自然对流条件下单个裂隙壁面上的结霜模型,并利用试验结果对结霜模型结果进行了验证。
1 试验及结果
1.1 试样制备
真实裂隙岩体是理想的试验对象,但考虑到实际裂隙岩体中,裂隙的走向往往是不规则的,裂隙中也经常有充填物,此外,岩石基质也多是非均质的,难以有效控制试验变量。因此,预制了A、B 两块水泥试块,每块的尺寸均为12 cm×5 cm×30 cm。水泥试块由P.O42.5 水泥和自来水拌和浇筑而成,水灰比(w/c)为0.5,试块浇筑好后在标准养护室内养护28天[T=(20±2) ℃,相对湿度RH>95%]。水泥试块的具体参数如表1所示。试块的孔隙率和抗拉强度接近粗砂岩,因此,水泥试块拼接裂隙岩体试样可近似看作是对粗砂岩裂隙岩体的模拟。

表1 水泥试块的物理力学参数Table 1 Physical and mechanical parameters of cement test block
将养护好的水泥试块A 和B 在水中浸泡7 天,使试块本身饱和,然后将两个试块的侧面(5 cm×30 cm)拼接在一起,形成具有单条垂直裂隙的岩体试样,裂隙中处于不饱和状态。
1.2 试验过程及装置
为了模拟底部有补给水分的寒区季节性冻土的降温过程,试样底部保持正温(+2 ℃),且具有恒定补水位,试样顶部保持负温(-5 ℃),试样处于单向冻结状态。具体试验装置如图1所示。监测整个试验过程中马氏瓶中水位的变化和试样中温度的变化,试验共持续约380 h,自260 h 起,马氏瓶中的水位基本保持不变。
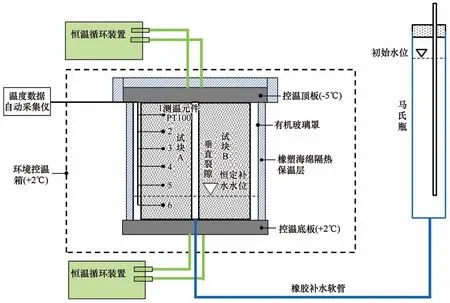
图1 试验装置图Fig. 1 Diagram of test setup
1.3 试验结果
1.3.1 结冰及开裂现象
试验完成后,拆除保温层及控温板,如图2 所示,试样顶部周边的负温区域有显著的结霜现象,霜层厚度在7~10 mm;当将两个试块拆开后,预制垂直裂隙中有显著的冰层生长现象,如图3 所示。此外,试样负温区出现4 条新增裂隙,分别为试块A上的水平裂隙A-1,垂直裂隙A-2及试块B上的水平裂隙B-1 及B-2,这些新增裂隙中均有薄冰层存在,其中3条水平裂隙可能是试块内水分迁移和冰分凝所导致,垂直裂隙则可能是原位冻胀导致。为了判断预制垂直裂隙中液态水迁移高度及位置,马氏瓶中添加了红色荧光染料,由图3可以看出,裂隙壁面上液态水迁移的最大高度为12 cm,尚未到达试样负温区。

图3 试验结束后的预制裂隙壁面冰层及新增裂隙Fig. 3 Ice layer on the wall of the prefabricated fracture and the new fracture after test
1.3.2 试样中的温度变化及负温区范围
从图4 可以看出,在试验开始后的前8 h 内,各个测点的温度曲线斜率很大,表明温度下降迅速,自第10 h开始,各测点的温度变化趋缓,18 h之后各测点的温度基本保持不变,温度曲线接近水平,说明此时整个试样已经与外界之间的热交换达到平衡,试样内部形成稳定的温度场,零度温度线位于2号测点和3号测点之间,即自试样顶部向下约10 cm范围内为负温区。
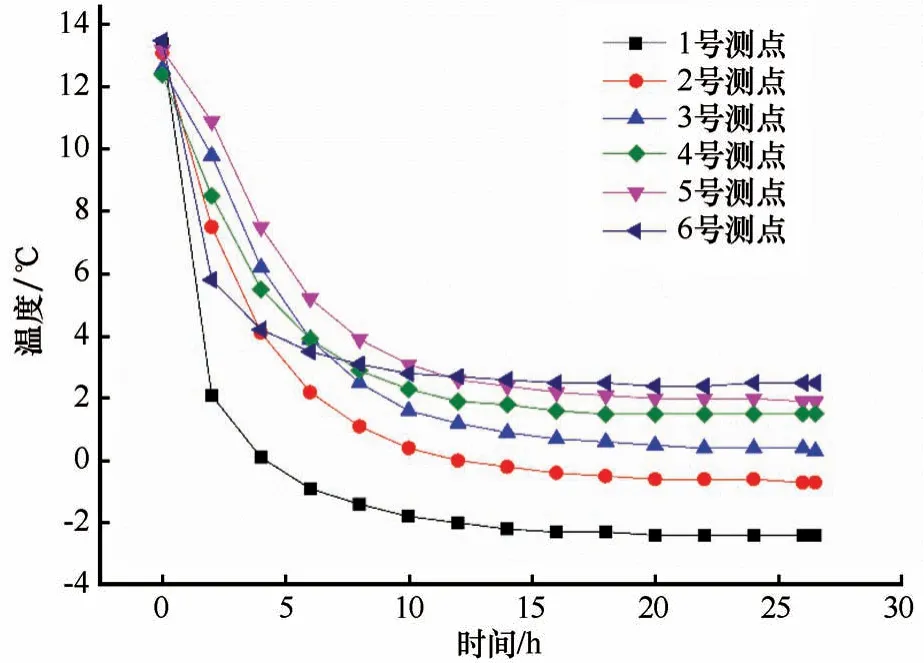
图4 试样中各测点的温度变化Fig. 4 Temperature change of each measurement point in the specimen
1.3.3 马氏瓶中的水位变化及总的迁移水量
在整个试验过程中,马氏瓶中的水位变化如图5所示。可以看出,试验开始的前150 h,即6天多的时间内,水位曲线斜率很大,表明在这个阶段水位下降迅速,试样内的水分迁移速度很快,随着时间推移,迁移速度在逐渐变小;150 h之后水位曲线趋向水平,直到260 h时,即试验进行到第11天左右,水位曲线逐渐接近水平,说明此时马氏瓶内的水位基本保持稳定,变化很小,表明试样内的水分迁移活动基本停滞或是处在一种动态的平衡之中。260 h 对应的水位刻度为5.67 cm,初始水位刻度为76 cm,则在整个试验过程中迁移水量为:(76-5.67)×3.14=221 mL。

图5 马氏瓶中水位变化Fig. 5 Change in water level in Mariotte’s bottle
1.3.4 水分迁移形态分析
对于本试验中的试样而言,水分可能迁移的路径分别为试块本身、试块A 和B 拼接形成的垂直裂隙、试样与有机玻璃罩之间的空隙。
Akagawa 等[14]曾对孔隙率为37.9% 的饱和Welded 凝灰岩试样(直径为29 cm,高为25 cm 的圆柱)进行单向冻结补水试验:试验共进行约1 000 h,试验结束后观察到有明显的水平分凝冰层。当试验进行到20 h 后,底部补水瓶中的液面开始出现下降,说明水分开始不断由试样暖端向冷端迁移,补给分凝冰的不断生长。但在整个试验过程中补水瓶中的液面总共下降了约2.4 cm,对应的迁移水量总计约为6.5 mL。本文试验中水泥试块的孔隙率为14.3%,对照来看的话,水泥试块中的液态水迁移量应该也是<10 mL的,与马氏瓶中最终显示的迁移水量(221 mL)相比,仍然是很少的;对于试块A和试块B 拼接形成的垂直裂隙而言,由于拼接时并未对裂隙进行饱和,因此垂直裂隙是不饱和的,其中应同时存在气态和液态迁移,由图3 可看到液态水迁移的最大高度为12 cm,尚未到达0 ℃线,假设裂隙宽度为1 mm,则裂隙中液态水迁移总量约为10 mL;对于试样与有机玻璃罩之间的空隙而言,试样侧壁与有机玻璃罩之间的距离为1.5~2.5 cm,难以形态液态水迁移通道。另外,试样负温区壁面冰层主要的呈现形态为霜,也可以推断是气态水在此遇冷凝华而成。
综上,对本试验中的试样而言,其水分迁移形态以气态水为主。
2 单个裂隙壁面上的结霜模型
由试验结果可以看出,整个单向冻结过程中,裂隙岩体试样底部的水分主要以气态形式沿着裂隙及岩样周边空隙向顶部迁移,并在试样的负温区凝华成霜。试样表面及裂隙壁面的结霜过程实际上是冷板面在自然对流条件下的传热传质过程。冷板面上霜层的真实生长过程非常复杂,为简化建模过程,进行了以下前提假设:霜层生长被视为准稳态过程[26];霜层生长被视为一维问题:即霜层在垂直冷板的方向生长[27];霜层中给定位置处的气相与固相温度相同[27];将岩石壁面上的霜层视为多孔介质;不考虑重力对霜层生长的影响;冷板及霜层生长空间中周围大气压保持不变,为1 个大气压(101 325 Pa);空气及其中的各组分符合理想气体定律。
尚未降温时,水蒸气在相对封闭的裂隙空间中处于平衡状态,即水蒸气处于饱和。当顶部冷板降温导致部分试样表面及裂隙壁面降至负温时,水蒸气在此遇冷凝华成霜,使得水蒸气迁移通道中的浓度梯度发生变化,导致了水蒸气的进一步迁移,同时也使得霜层不断生长,此时霜层与周围湿空气之间的传热以自然对流为主,当相邻壁面有温度差时,还会有辐射传热。取裂隙一侧的壁面作为分析对象,建立坐标系如图6所示。
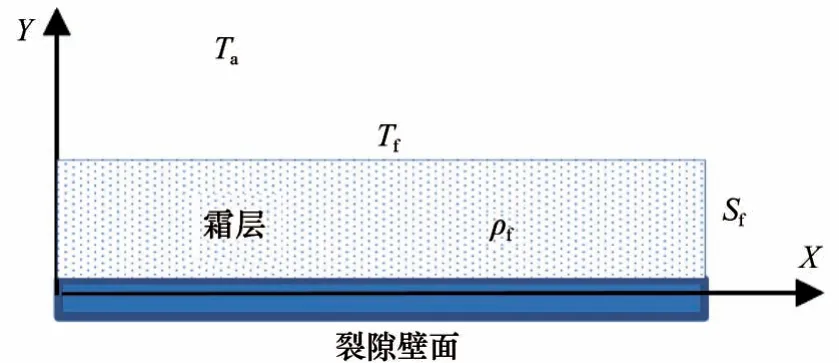
图6 霜层在裂隙壁面上的生长示意图Fig. 6 Schematic diagram of the growth of frost layer on the fracture wall surface
通过霜层的总的热通量(W·m-2)为对流传热、相变潜热及辐射传热的总和[28],即:
式中:h为对流传热系数(W·m-2·K-1);mv为水蒸气的质量通量(kg·s-1·m-2);L为凝华潜热(J·kg-1);σ为Stefan-Boltzmann常数(=5.7×10-8W·m-2·K-4);Ta、Tf和Tp分别为湿空气温度、霜层表面温度及裂隙壁面对面的壁面温度(K)。fr为辐射系数,取决于霜层、霜层对面岩石壁面的辐射系数及二者之间的几何因子,一般取fr= 0.8。
水蒸气传递到霜层的质量通量mv与传质系数hD(m·s-1)有关,表示为:
式中:ρv,a为湿空气中的水蒸气密度(kg·m-3);ρv,f为霜层表面的水蒸气密度(kg·m-3)。
总的热通量q和霜层的有效导热系数kf(W·m-1·K-1)相关,表示为
式中:Tw为冷板的表面温度(K);Sf为霜层厚度(m)。将式(1)~(3)结合起来可得:
其中凝华潜热L为:
最终,在给定时间间隔Δτ内沉积的霜层质量ΔM(每单位面积)为
当给定空气温度、相对湿度和冷板表面温度时,可用式(3)、(4)和(6)确定霜层生长期间冷板上的霜层厚度、霜层表面温度和热通量。
3 计算及验证
3.1 计算过程及计算时长
自然对流传热区分为大空间自然对流和有限空间自然对流。岩体裂隙中的对流传热过程均归属于有限空间自然对流。裂隙夹层内的流动主要取决于以夹层厚度δ为特征尺度的格拉晓夫数Gr。对于竖夹层当Gr≤2 860;对水平夹层(底面为热面)当Gr≤2 430 时夹层内的热量传递依靠导热。当Gr数超过上述数值时,夹层内开始形成自然对流,并且随着Gr数的增加,对流的展开越来越强烈[28]。首先利用格拉晓夫数Gr判断相应的壁面是否符合结霜计算条件:即对于竖夹层Gr>2 860,对于水平夹层(底面为热面)Gr>2 430。当符合结霜条件时,计算对流换热系数,然后计算霜层厚度、霜层表面温度及总的水蒸气通量。利用数值计算软件MATLAB将上述计算过程进行编程。
由图5 可知,当试验进行至约260 h 时,马氏瓶内的液面基本保持不变,也即意味着岩体裂隙试样中不再发生水分迁移,或水分迁移处于一种动态平衡过程。因此,结霜计算时间也取为260 h,每个计算时间步长为1 h,即3 600 s。
3.2 试样中冷表面的构成
试样由试块A 和试块B 拼接而成,试样顶部控温板为-5 ℃,试样底部控温板为+2 ℃,当试样内温度稳定后(约试验开始后18 h),0 ℃等温线约在试样顶部向下10 cm处,即由试样顶部向下约10 cm范围内为负温区。如图7 所示,试块A 在负温区的冷表面有正面c1 面,背面c2 面,侧面d1 面,既有裂隙壁面e1 及顶面f1;试块B 在负温区域的冷表面有正面c3 面,背面c4 面,侧面d2 面,既有裂隙壁面e2 及顶面f2。

图7 试样中的冷表面构成示意图Fig. 7 Schematic diagram of the cold surface composition in a specimen
试块A和试块B的尺寸均为12 cm×5 cm×30 cm(长×宽×高),其中涉及的具体冷表面因所处位置不同,决定了计算总的热通量时是否考虑辐射传热,如冷表面c1~c4、d1、d2 的对面为有机玻璃壁面,冷表面与对面壁面(+2 ℃)之间存在温差,因此需考虑辐射传热;而冷表面e1 与e2 为垂直裂隙的两侧壁面,互相之间无温差存在,不需考虑辐射传热;f1 与f2 虽为冷表面,但不在所模拟的裂隙系统内,水蒸气难以到达,试验结束后也未观察到结霜现象,因此不考虑f1 与f2 面。除此之外,为了保证整个系统处于相对封闭的状态,试样顶部与周围有机玻璃筒之间用胶带进行粘接,胶带面也形成了水平冷表面,试验结束后观察到了霜层的出现。具体冷面积的大小及结霜类型如表2所示。

表2 冷表面的面积大小及结霜类型Table 2 Size of cold surface area and type of frosting
如图3所示,当试验结束后,在试样的负温区出现了4 条新增裂隙,分别为水平裂隙A-1、B-1 及B-2,垂直裂隙A-2。每新增一条裂隙则意味着新增两块冷表面。对于新增水平裂隙中的冷表面而言,其中的格拉晓夫数Gr远小于2 430,即意味着其中基本不存在对流传热,因此裂隙两侧冷表面上也就不可能出现结霜过程,对于垂直裂隙A-2而言,其两侧壁面特性与e1/e2面相似,归为同一类考虑。
3.3 不同冷表面结霜计算结果
3.3.1 垂直冷表面,有辐射传热(I类)
计算结果如图8所示,分别为霜层厚度、霜层密度及单位面积上霜层质量随时间t(h)的变化。可以看出,随着结霜时间的增加,霜层厚度在不断增加,霜层厚度与时间呈线性关系,最终厚度为9.6 mm,与试验结果非常接近;霜层密度初始当设Tf=Tw时计算结果为208.9 kg·m-3,在第2个时间步计算时即有一个大的突变,为368.53 kg·m-3,之后随着结霜过程的进行,霜层密度小幅增加,第260 h 时霜层密度为370.12 kg·m-3;由于在整个结霜过程中密度基本保持不变,而厚度线性增加,则最终单位面积上霜层的质量也呈现为线性增加,最终单位面积上的霜层质量为3.55 kg·m-2。

图8 I类冷表面上霜层厚度、密度及单位面积霜层质量随时间的变化Fig. 8 Variation of frost thickness (a), density (b) and frost mass per unit area (c) on type I cold surface with time
3.3.2 垂直冷表面,无辐射传热(Ⅱ类)
计算结果如图9所示,分别为霜层厚度、霜层密度及单位面积上霜层质量随时间t(h)的变化。可以看出,随着结霜时间的增加,霜层厚度在不断增加,霜层厚度与时间呈线性关系,最终的厚度为5.1 mm,与试验结果有一定差距;霜层密度初始(Tf=Tw)时计算结果为208.9 kg·m-3,在第2个时间步计算时即有一个大的突变,为368.68 kg·m-3,之后随着结霜过程的进行,霜层密度逐渐增加,第260 h 时霜层密度为382.38 kg·m-3;单位面积上累积的霜层质量也呈现线性增加趋势,最终单位面积霜层质量为1.92 kg·m-2。

图9 Ⅱ类冷表面上霜层厚度、密度及单位面积霜层质量随时间的变化Fig. 9 Variation of frost thickness (a), density (b) and frost mass per unit area (c) on type II cold surface with time
3.3.3 水平冷表面,有辐射传热(III类)
计算结果如图10 所示,分别为霜层厚度、霜层密度及单位面积上霜层质量随时间t(h)的变化。可以看出,随着结霜时间的增加,霜层厚度在不断增加,霜层厚度与时间呈线性关系,最终的厚度为17.9 mm,大于试验结果;霜层密度初始(Tf=Tw)时计算结果为208.92 kg·m-3,与前两种工况不同的是:随着结霜过程的进行,霜层密度逐渐减小,第260 h 时霜层密度为186.06 kg·m-3,霜层密度与时间呈现线性递减关系;单位面积上累积的霜层质量呈现线性增加趋势,最终单位面积质量为3.55 kg·m-2。
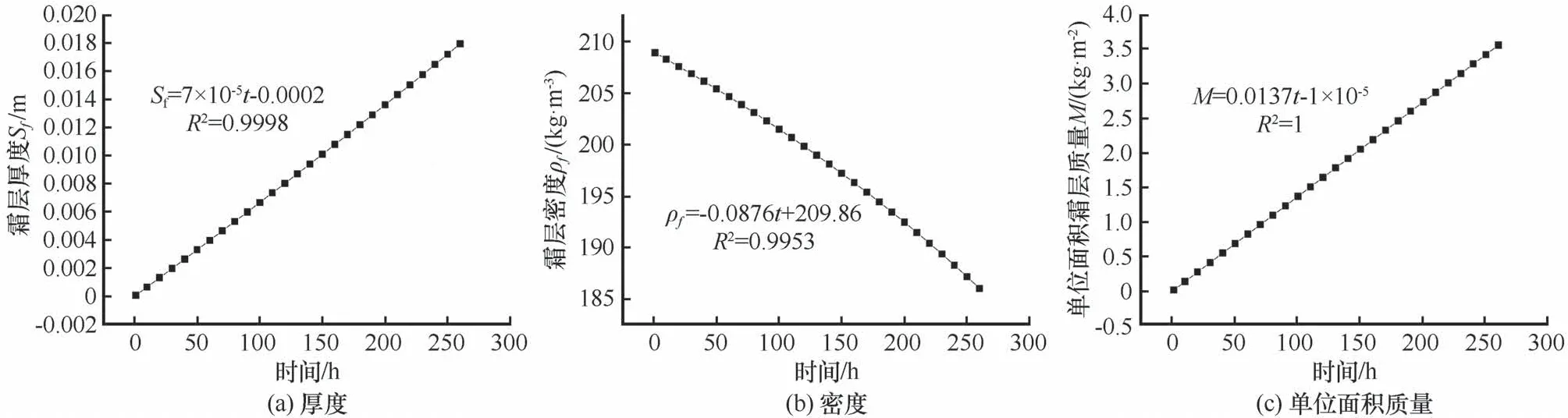
图10 III类冷表面上霜层厚度、密度及单位面积霜层质量随时间的变化Fig. 10 Variation of frost thickness (a), density (b) and frost mass per unit area (c) on type III cold surface with time
3.4 结霜计算结果与试验结果对比分析
3.4.1 结霜厚度对比
由表3 可以看出,对于I 类冷表面,模型计算结果与试验结果吻合良好;对于II、III 类冷表面,霜层计算结果较试验结果偏大。Ⅱ类表面是垂直裂隙的两侧壁面,此类裂隙中冰层生长过程除了结霜作用外,还可能存在复杂的霜冰转换过程:由密度较低的霜层多孔介质向密实的冰层转变,即进入了霜层生长的第三阶段——霜层充分发展阶段,而目前所建的结霜模型中仅将霜层视为多孔介质;对于III类冷表面,即胶带面而言,受重力作用影响显著,但结霜模型中尚未考虑重力效应。因此,II、III类冷面板上计算出的霜层厚度与试验结果相比有较大差距。

表3 冷表面上结霜计算厚度与试验厚度对比Table 3 Frosting calculation thickness and test thickness comparison on cold surface
3.4.2 计算结霜质量与实测水分迁移质量对比
依据试验条件,试样周围环境接近密封,试验过程中可以观察到绝大部分水分以水蒸气形式迁移至试样负温壁面凝华成霜,依据质量守恒定律,水分的迁移量应与结霜模型中计算的累积霜层质量M一致。将试验中记录的水分变化量与结霜质量M表示在图11中,由于自第50 h到第80 h数据采集仪故障,故此部分的水分迁移量缺失。
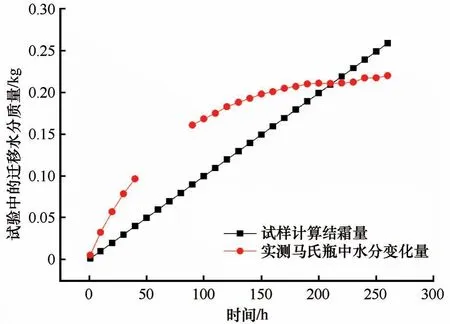
图11 试样计算结霜质量与实测马氏瓶中水分变化量随时间的变化Fig. 11 Variation of the calculated mass of frosting in specimen and the measured amount of moisture change in Mariotte’s bottle with time
由图11 可以看出结霜计算量与时间呈现线性关系,而实际记录的水分迁移量曲线则先增大,后减缓增大趋势直至接近水平,即水分迁移量不再变化。二者之间的趋势是一致的,但存在一定的偏差,可能的原因有结霜模型本身的准确性,另一方面为水蒸气迁移还有别的通路,如通过水膜补给冰层生长等。但大致可以以结霜模型中的霜层累积质量估算气态迁移的水量。
4 讨论
4.1 影响裂隙壁面结霜的直接因素
以结霜模型的计算结果为依据,同时结合两篇综述性文献[29-30]中的相关总结,分析岩体裂隙负温区壁面结霜量及形态的直接影响因素。主要有以下几个方面:
(1)冷壁面温度:岩石裂隙壁面温度越低时,则霜层厚度越大,霜层密度越小,即冷壁表面形成霜层的速度快,但密度较低,霜层相对蓬松;壁面温度越高时,则霜层厚度较小,霜层密度较大,即形成的霜层较为密实。
(2)空气中的相对湿度:相对湿度越大,意味着空气中水蒸气含量越高,则霜层厚度越大,霜层密度越大,一定时间内单位面积内累积的霜层质量越多。
(3)对流传热系数:对流传热系数代表了岩石冷壁附近空间的对流状态,当对流越强烈时,则意味着传热传质过程越强烈,霜层厚度越大,霜层密度越大,水蒸气传递到霜层的质量通量也越大,则一定时间内单位面积内累积的霜层质量越多。
(4)冷壁面面积:即负温区的面积,裂隙中总的累积结霜质量与水蒸气传递到霜层的质量通量、时间及冷壁面面积相关,时间一定时,水蒸气的质量通量一定时,冷壁面积越大,则累积霜层质量越大。
因此,当岩体裂隙中对流传热较为强烈、裂隙中相对湿度较大且负温区壁面面积较大时,一定时间内裂隙冷壁面上的结霜量会比较多,伴随后期的霜冰转化过程,裂隙中的冰层生长会比较显著;裂隙冷壁面上温度(<0 ℃)的高低会直接影响霜层的形态,壁面温度较低时,霜层较为蓬松,壁面温度较高时,霜层较为密实。
4.2 温度梯度的影响
由结霜模型和4.1 节的分析可以看出,低温岩体中的温度梯度在结霜过程中无直接的影响。但实际上,温度梯度是整个结霜过程中的更为本质的因素,温度梯度通过影响4.1 节中的直接因素而影响整个结霜过程。
当地表温度越低时,裂隙沿程的温度梯度越大,一方面会影响裂隙中冷壁面附近的对流传热状况,温度梯度越大,则相同空间中的对流传热系数越大;另一方面,温度梯度越大也即意味着裂隙中负温壁面面积越大。所以,当温度梯度越大时,裂隙中冷壁面上的结霜量会越多,意味着加快了裂隙中的成冰过程。当温度梯度越小时,则裂隙中冷壁面上的结霜量会比较少,即裂隙中的成冰过程比较缓慢。
5 结论
为研究非饱和岩体裂隙中冰层生长及相关影响因素,作者对含有单条垂直裂隙岩体试样进行了底部补水条件下的单向冻结试验。基于热力学基本原理,建立了自然对流条件下单个裂隙壁面上的结霜模型,并利用试验结果对结霜模型结果进行了验证。主要结论如下:
(1)当岩体裂隙负温区壁面所处空间中以对流传热为主时,壁面附近的水蒸气遇冷凝华成霜,可以推断的是随着霜层的生长及后续的霜冰转化,有可能在裂隙中形成比较明显的冰夹层,从而导致裂隙的进一步扩展。这个推断还需将来进一步的研究证实。
(2)基于热力学基本原理建立了岩石冷壁面的结霜模型,依据对流条件将岩体冷壁面分为四类,前三类满足结霜模型的相关条件,然后对这三类壁面进行了结霜计算。计算结果与试验结果吻合良好。
(3)基于结霜模型,分析了影响结霜和水蒸气迁移的相关因素:对流传热条件,裂隙中的相对湿度及负温区壁面面积大小是3 个直接因素,这3 个因素取值越大时,则一定时间内结霜量越多也意味着水蒸气迁移量越大,裂隙中的成冰作用更为显著。裂隙沿程的温度梯度是更为本质的原因,温度梯度越大时,岩体裂隙中的对流传热作用会更为强烈,负温区壁面面积越大,则一定时间内结霜量越多,气态水迁移量越多。

