基于非监督分类和图优化的GNSS多路径误差削弱方法

丁 杨 赵乐文 李飞翔

1 南京信息工程大学遥感与测绘工程学院,南京市宁六路219号,210044 2 江苏省协同精密导航定位与智能应用工程研究中心,南京市宁六路219号,210044 3 自然资源部遥感导航一体化应用工程技术创新中心,南京市宁六路219号,210044

随着多系统GNSS的不断发展,城市环境下的可观测卫星数量显著增加,有助于提高GNSS定位的可用性。但城市环境下GNSS信号传播易受建筑物及树木遮挡,导致接收机观测值受多路径误差干扰,定位精度降低。多路径信号可分为视线(line-of-sight,LOS)和非视线(non-line-of-sight,NLOS)多路径误差,LOS多路径误差是接收机接收到反射/衍射信号所致,对伪距观测值的影响一般为m级,且可以采用扼流圈天线或改进接收机信号跟踪算法进行抑制[1];NLOS多路径效应是非直射路径上的卫星信号通过反射/衍射被接收机接收,根据观测环境的不同其误差可达数十米甚至上百米[2]。

为了削弱多路径信号的影响,有学者提出基于高度角、信噪比等数据质量指标的定权算法[3],然而在复杂区域,由于所选数据质量指标与NLOS多径误差间的相关性难以定量描述,因此该方法改善定位精度的效果并不显著。为此,有学者引入机器学习算法,利用数据质量指标进行GNSS信号分类,以分离直射信号、LOS多路径信号和NLOS多路径信号。常用的机器学习方法包括监督学习和非监督学习,其中监督学习算法需要利用坐标已知的参考站对GNSS信号进行预分类,构造表征信号质量特征的向量进行模型训练,以便用于流动站信号分类。常用的训练模型有支持向量机分类器、决策树算法和神经网络算法等[4-6],但这些算法需要事先建立样本集,难以满足城市环境下不同复杂场景的应用需求。朱斌等[7]对比了K-means++、高斯混合和模糊c-均值3种不同聚类方法的性能后发现,K-means++算法具有较优的分类性能,对伪距定位水平和高程方向的精度提升均达50%以上。

此外,有学者提出利用多传感器融合[8]和抗差估计方法[9]削弱NLOS多路径信号对定位的影响,但在复杂观测环境下,多路径信号会污染观测噪声的零均值分布特性,造成Kalman滤波偏差,甚至发散。图优化作为同步定位与建图(SLAM)领域的主流优化算法,能够对历史信息和多普勒信息进行有效利用,并于2012年被首次应用于GNSS定位[10]。有学者进一步将伪距、载波相位、多普勒观测量添加为因子节点,以提高定位精度[11],结果表明,其对伪距定位和差分定位的精度提升约为20%～40%。

伪距单点定位是GNSS数据预处理的重要环节,可用于异常卫星的识别和剔除,为进一步的载波差分定位和精密单点定位提供精确的初始坐标。非监督分类和图优化方法均能实现对NLOS多路径误差的抑制和剔除,但二者原理不同,且对SPP精度的改善效果不明确。因此,本文基于城市环境下采集的GNSS数据,评估2种算法对SPP精度的改善效果,对城市环境下接收机数据预处理方法的选择具有参考意义。

1 数学模型

GNSS伪距单点定位的观测方程可表示为:

(1)

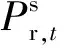
伪距单点定位的误差函数可以表示为:

(2)

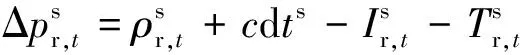
1.1 K均值非监督分类方法

K均值(K-means++)算法是对样本空间中的数据集按照一定特征进行聚类,通过迭代算法查找最优聚类中心,使之满足同一聚类中样本差异小、不同聚类间样本差异大的条件,选择合适的特征向量构建样本空间。本文选取GNSS数据处理中能够表征信号质量的指标,即观测值的载噪比、卫星高度角和伪距定位残差,构建样本空间进行聚类分析。由于不同质量指标存在量纲差异,首先需要进行归一化处理,然后通过迭代算法计算每个聚类空间中样本与聚类中心的误差平方和,当变化最小时停止迭代。K均值分类的目标函数可以表示为:

(3)

式中,K为聚类中心个数,μi和Ci分别为第i个聚类空间中的聚类中心和特征向量的集合。聚类中心的迭代计算方法详见文献[7]。

1.2 图优化方法

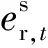
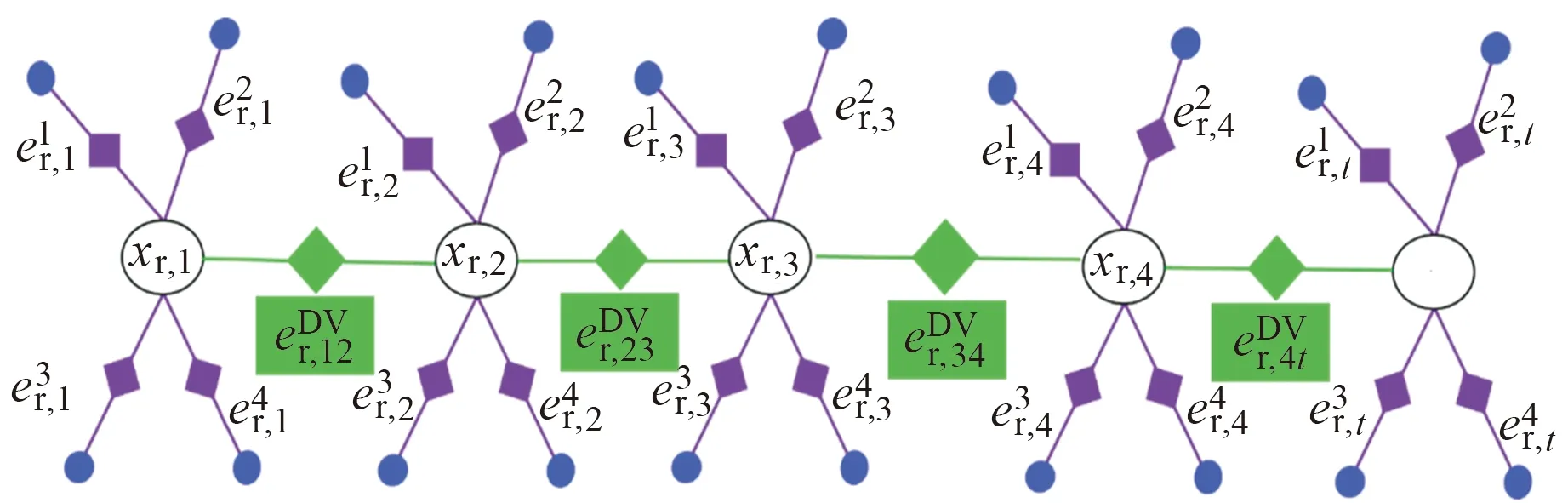
图1 伪距定位的图优化结构

(4)

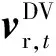
因此,基于图优化的伪距/多普勒融合定位目标函数可以表示为:

(5)

2 实验结果与分析

2.1 数据采集与处理

实验采用多系统、多频率的GNSS接收机模块进行城市环境下静态观测数据的采集。数据采样率为1 s,观测时段为2021-04-15 03:00:00～05:00:00,观测环境及卫星的天空分布如图2所示。由图可见,环境周边存在高楼、树木等遮挡,因此西向和南向数据的可用性和连续性较差。图3为不同系统可见卫星数量的变化情况,观测时段内GPS、Galileo、GLONASS、BDS四系统的平均可见卫星数量分别为6、4、5、11颗,其中BDS的可见卫星数量最多,说明BDS在复杂观测环境下具有显著优势。四系统平均可用卫星数量为25颗,但卫星数量随时间显著变化,主要是由于观测环境的遮挡导致部分卫星信号存在异常。

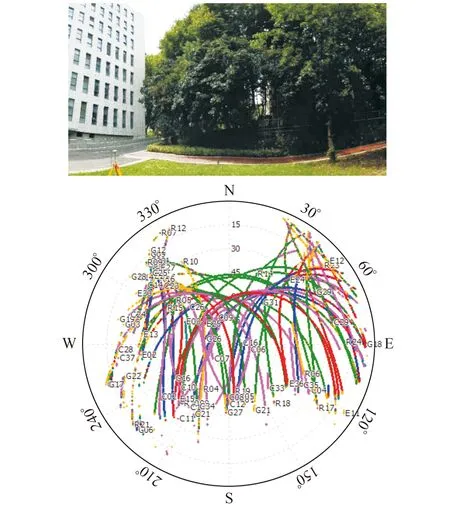
图2 GNSS观测数据采集环境及对应的卫星天空视图

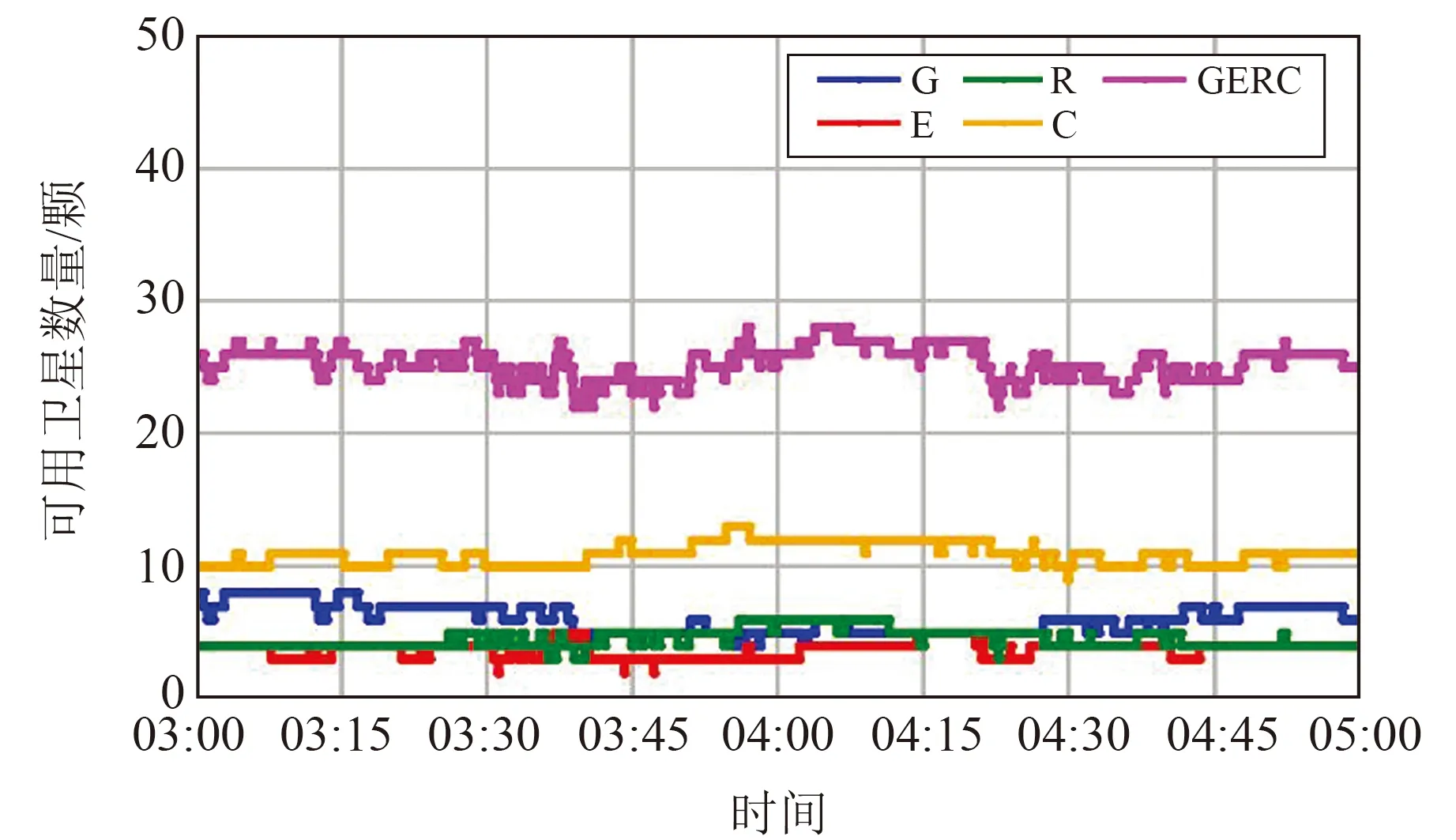
图3 不同GNSS系统可用卫星数量变化情况

基于开源GNSS数据处理软件RTKLIB进行二次开发,实现K-means++非监督分类算法和图优化方法,传统SPP采用多系统、单历元最小二乘方法,为定量评估SPP精度,需要获取高精度参考坐标。选取附近Trimble Alloy接收机作为参考站,进行短基线解算以获取流动站接收机的参考坐标,参考站坐标通过静态PPP解算得到,可以达到mm级定位精度。由于受遮挡环境影响,流动站接收机数据质量较差,因此利用常规手段进行静态差分RTK解算的模糊度固定率和定位精度较差。本文对比了3种不同处理策略的RTK定位精度:1) “15ele”模式,采用15°截止高度角进行RTK解算;2)“50ele”模式,采用50°截止高度角进行RTK解算;3)“15excl”模式,首先基于事后的站间单差伪距残差分布剔除异常的卫星[12],然后以15°截止高度角进行RTK解算。

图4为不同解算模式下的静态差分定位误差序列对比。采用“15ele”模式进行解算的模糊度固定率为0,且定位误差较大,主要是因为低高度角卫星受遮挡环境影响导致信号多路径误差较大。“50ele”和“15excl”模式下的RTK模糊度固定率分别为51.6%和91.2%,表明即便采用大高度角的卫星进行多系统组合解算,模糊度固定率仍然较低,当手动剔除受遮挡环境影响的卫星后,模糊度固定率显著提高。因此,本文以“15excl”模式静态RTK固定解坐标的平均值作为流动站坐标的参考值进行后续伪距定位精度评估。

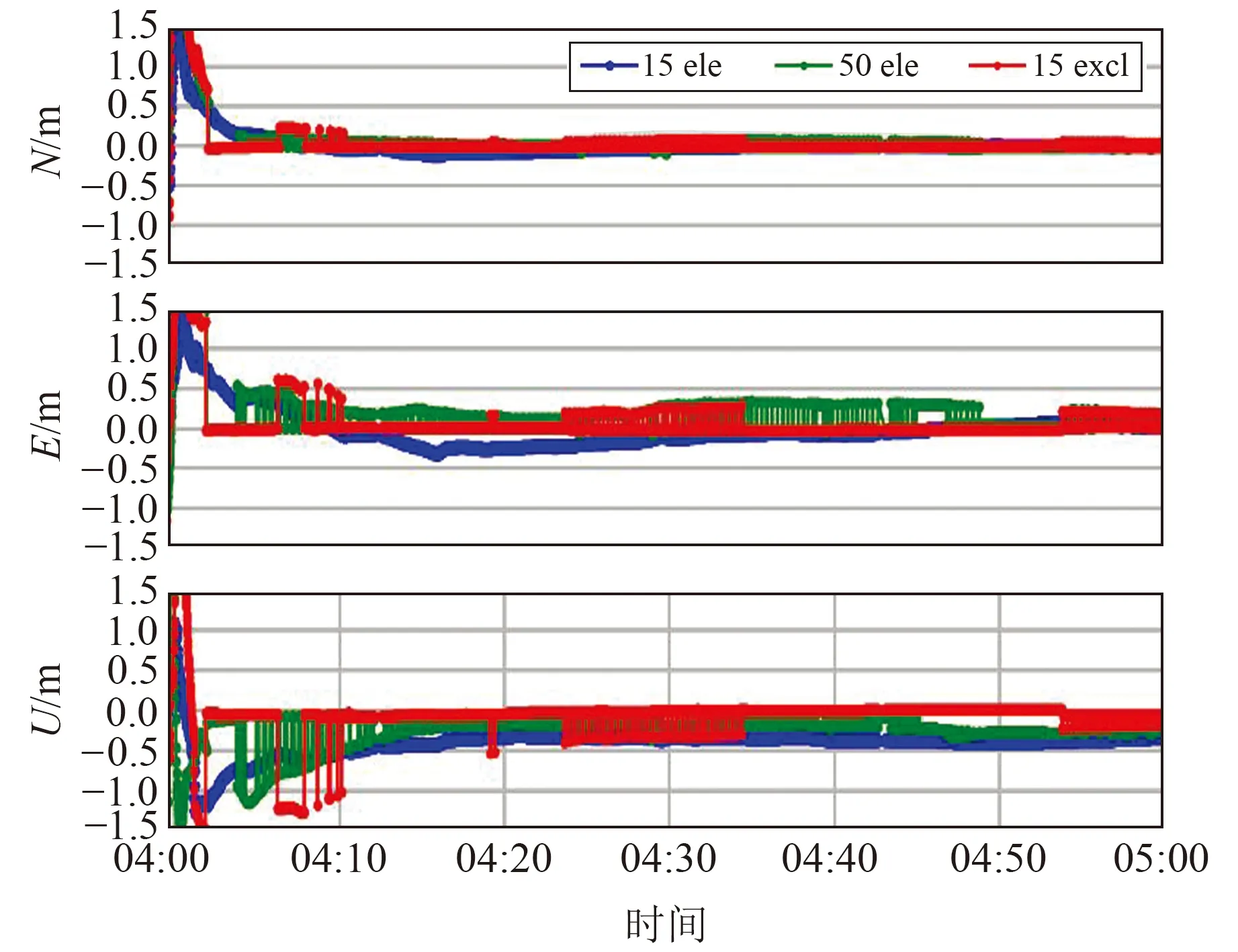
图4 不同定位模式下RTK定位误差时间序列

2.2 基于K-means++算法的伪距定位精度评估

图5为不同解算模式下SPP误差时间序列。由图可见,“15ele”模式下水平方向的定位精度优于20 m,高程方向的定位精度优于50 m,主要是因为NLOS信号会给定位带来一定的系统误差。“50ele”模式对水平方向的定位精度改善较为显著,高程方向的定位精度改善较小,且个别历元在水平和高程方向的精度变差,主要是因为大截止高度角导致可用卫星数量减少,卫星空间几何分布变差。“15excl”模式对SPP精度的改善效果显著,说明剔除多径信号有助于提高伪距定位精度。图6为采用传统算法(“15ele”)和K-means++算法(“15ele-K-means++”)剔除NLOS信号前后定位误差的时间序列,由图可见,通过分类剔除LOS和NLOS多路径观测值后,“15ele-K-means++”模式下SPP水平方向的定位精度显著提升,高程方向的定位结果在04:00～04:45时间段内存在较大偏差,这可能是聚类错误引起LOS可见卫星数量减少、卫星空间几何分布变差所致。

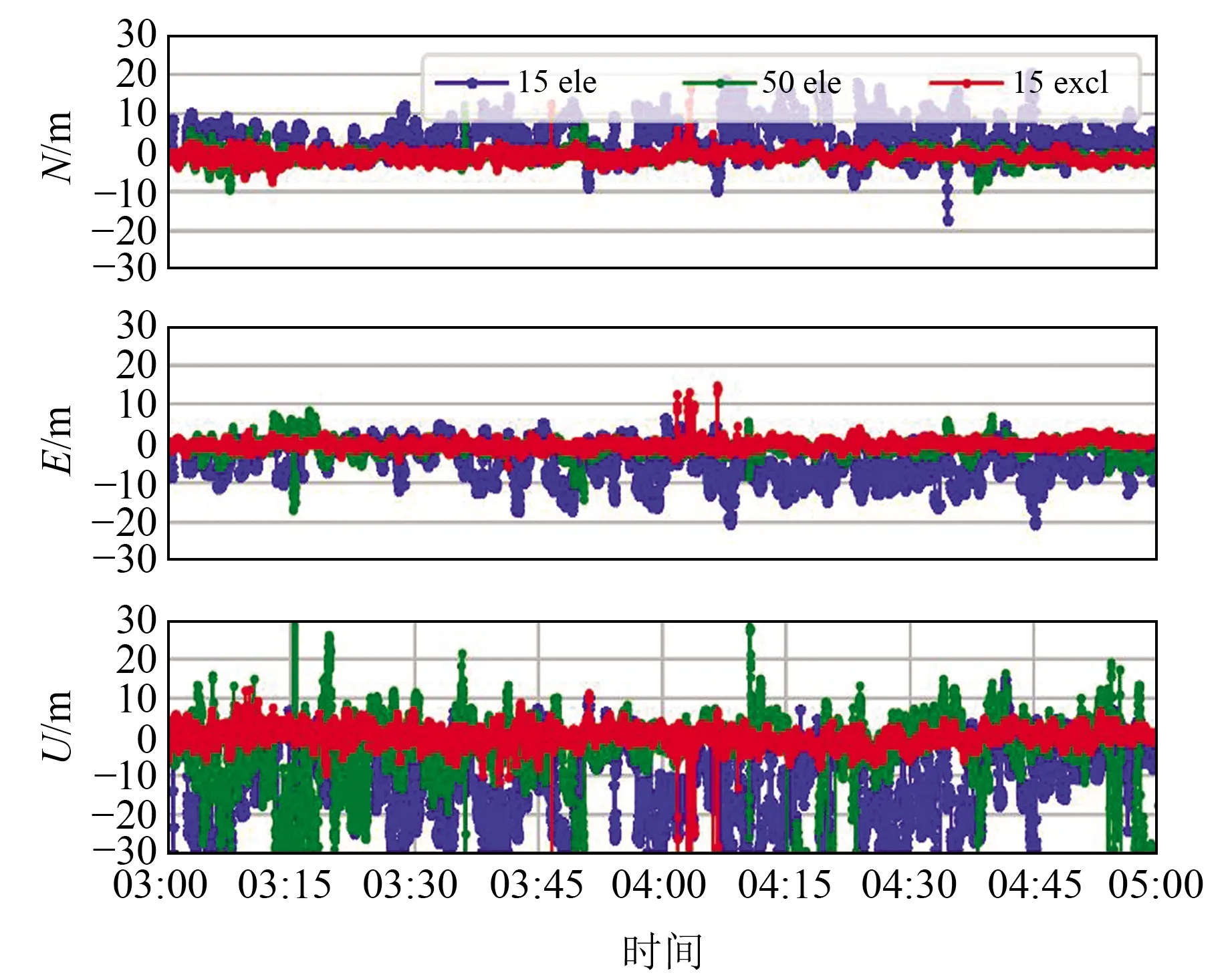
图5 不同定位模式下SPP的误差序列

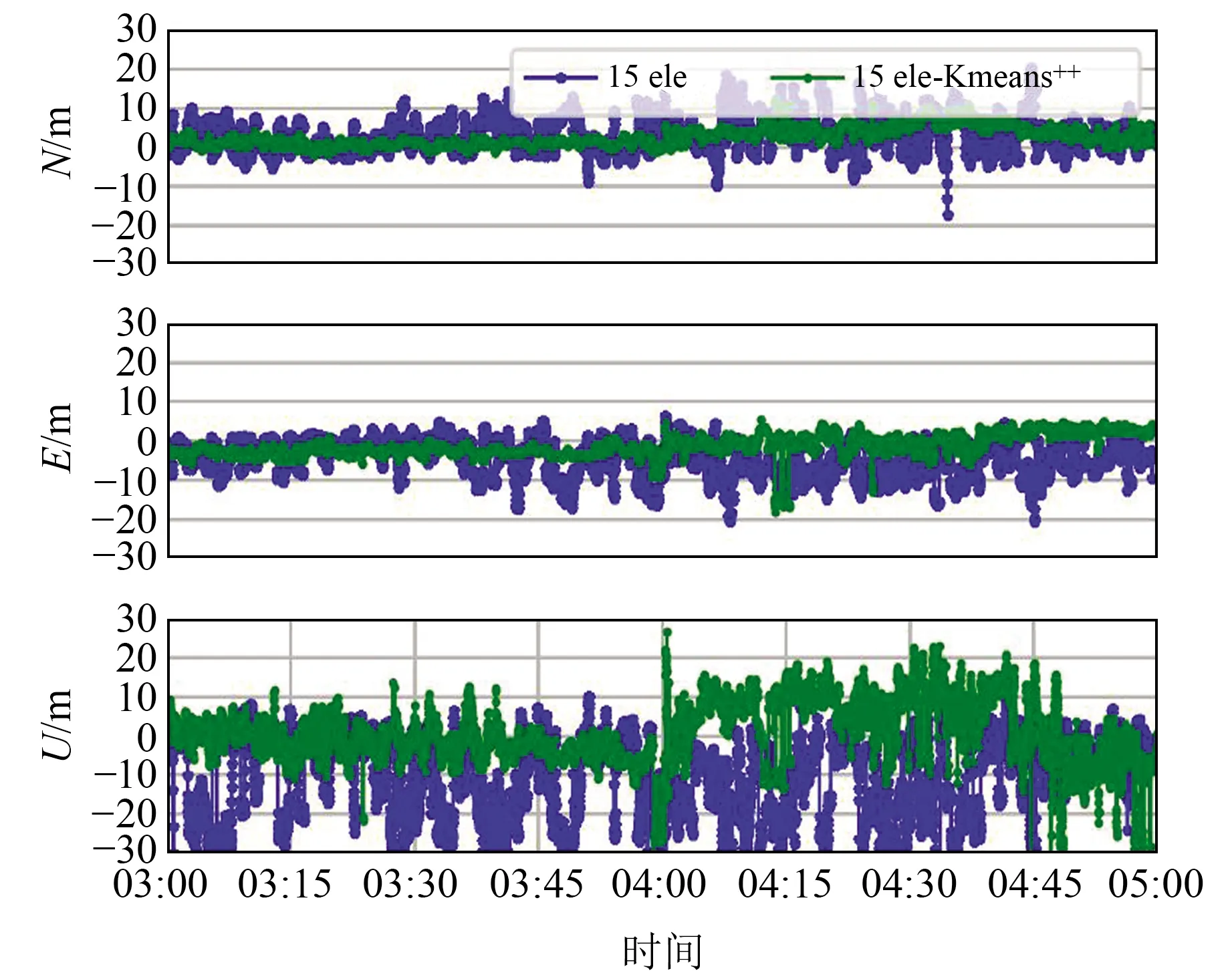
图6 基于传统策略和K-means++算法的SPP定位误差序列

表1(单位m)为不同模式下N、E、U方向的定位误差序列的均方根RMS值。由表可见,采用大高度角“50ele”模式进行定位解算时,N、E方向的定位精度较传统“15ele”模式分别提高71%和62%,U方向的精度提高15%。聚类分析解算 “15ele-K-means++”模式下,水平和高程方向的定位精度较传统“15ele”模式提升约34%～54%,该模式下水平方向精度较“50ele”模式稍差,而高程方向精度优于“50ele”模式,主要是因为“50ele”模式解算中大高度角剔除了部分NLOS观测值,导致可用卫星数量变少,高程方向精度改善有限。“15excl”解算模式中剔除了NLOS信号卫星,其水平和高程方向的定位精度较传统“15ele”模式提升74%～82%,精度显著优于其他解算模式。“15ele-K-means++”模式的解算精度较“15excl”模式差,主要是由于观测值与分类器的特征向量之间不存在强相关性,导致分类精度不高,未能完全剔除多路径误差。

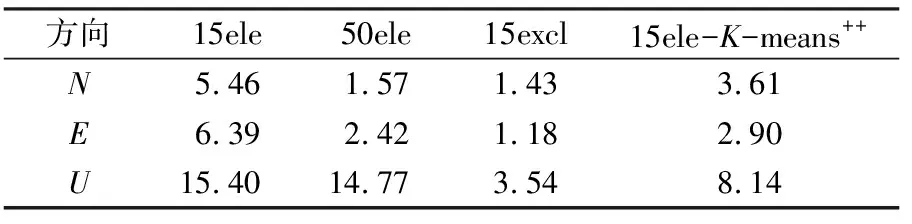
表1 不同模式下SPP的RMS

2.3 基于因子图优化的伪距定位精度评估

图7和8分别为15°和50°截止高度角情况下传统方法和图优化方法的SPP误差时间序列。由图7可知,15°截止高度角情况下图优化方法“15ele-FGO”在N、E、U方向的定位精度分别为5.46 m、6.39 m、15.40 m,较传统SPP“15ele”模式的精度分别提升82.8%、79.0%、82.0%。此外,“15ele-FGO”模式下的定位精度优于“15excl”模式,主要是由于图优化方法在削弱NLOS多路径信号影响的同时,并不减少可见卫星数量。由图8可见,相比于传统“50ele”模式,大截止高度角情况下的图优化方法在高程方向的精度提升显著,水平方向的精度改善较小。“50ele-FGO”模式在N、E、U方向的精度分别为1.03 m、1.23 m、4.64 m,分别提升33.5%、48.8%、69.3%,主要是由于图优化模型中多普勒测速因子的引入减少了历元间坐标的误差变化。

3 结 语

1)受城市环境中高楼和树木等遮挡因素的影响,GNSS信号的连续性和观测值精度会显著下降,导致RTK解算中模糊度固定率较差。通过事后分析剔除受遮挡环境影响的卫星后,RTK模糊度固定率能达到90%以上。

2)通过选取表征观测值质量指标的信号载噪比、卫星高度角和伪距定位残差构成特征向量,利用K-means++非监督分类算法进行NLOS多路径信号的剔除。结果表明,非监督分类算法解算得到的N、E、U方向的精度较传统方法提升34%～54%,其中E方向的精度提升最为显著,U方向的精度提升有限。

3)通过在图优化模型中引入多普勒速度约束因子,利用最优估计方法实现多路径信号和粗差的探测与剔除。结果表明,该算法能够在不显著减少可见卫星数量的情况下提高定位精度,N、E、U方向的精度较传统方法提升78%～82%。即使采用50°大截止高度角进行解算,图优化方法较传统最小二乘算法定位精度提升仍可达30%～66%。

本文分析表明,由于观测值质量与特征向量相关性难以定量描述,导致非监督分类算法对复杂环境下定位精度的提升有限;而图优化方法充分利用多普勒观测值的历元间相关性,通过全局优化减弱多路径信号的影响,优势明显。未来将研究采用图优化算法进行GNSS精密定位预处理,实现复杂观测环境下异常卫星剔除和精确坐标初值获取,提高GNSS定位性能。