油浸式电力变压器维修决策技术的研究
冯 凯
(中海石油(中国)有限公司湛江分公司,广东 湛江 524057)
随着社会对电力使用需求不断增加,越来越多的两级区域电网彼此互联,逐渐形成一个紧密相连的大型联合电网,而这一现象的发展被认为是今后电网继续推进和发展的必然趋势。互联多级电网最显著和最基本的特征是其骨干网络由高压、特高压输电网络构成。当前,大量的电站和用电区域通过高压线路连接而成,在这种架构下,电网彼此相连,构成了一个整体输配电网[1]。大电网的兴起,使长期以来的城市供电模式发生了变化。
油浸式电力变压器是我国输、配电网中的一种非常重要的变电装置,此装置承担着转换、传输能量的功能。变压器一旦发生故障,不仅会导致电网出现供电不稳定的现象,严重情况下,还会造成整个电网发生瘫痪,从而引发一系列的“链式反应”,对市场内的电力企业和国家造成巨大的经济损失,甚至会危及人身安全,引发现场火灾事故[2]。安全、可靠、经济的变压器保护是减少电网发生故障的重要途径[3]。据调查显示,在我国,供电可靠性较高的省份,供电可靠率达到了99.93%,而国外部分发达国家的供电可靠率却可以达到99.998%,通过比较,可以明显看出,国内供电可靠率仍有待进一步提升。为解决这方面问题,该文将在这次研究中,以某油浸式电力变压器为例进行设计。
1 故障树数学模型
在这个过程中,可假设x(t)为底层事件在时间t时的状态,计算,如公式(1)所示。
式中:当x(t)为1时,代表底层事件在时间t时发生,反之,当x(t)为0时,代表底层事件在时间t时不发生。综合上述分析,底层事件在时间t时发生的概率与随机事件的期望值相同,假设随机事件的期望值为pi(t),则有以下计算公式,如公式(2)所示。
式中:E为概率函数。在上述内容的基础上,用M(xt)为顶层事件在时间t时的状态,则有如下计算公式,如公式(3)所示。
式中:当M(xt)为1时,代表底层事件在时间t时发生,反之,当M(xt)为0时,代表底层事件在时间t时不发生。此时,顶层事件在时间t时发生的概率可以通过以下公式计算得到,如公式(4)所示。
式中:X为顶层事件发生的期望值。在上述内容的基础上,建立故障树数学模型,计算对应“门”与“或门”的发生概率。计算如公式(5)、公式(6)所示。
式中:PAND为对应“门”事件的发生概率。POR为对应“或门”事件的发生概率。n为事件的发生次数。i为事件发生条件。
2 构建油浸式电力变压器综合故障树模型
在上述内容的基础上,应明确在当前的电网工程中,变压器是最为重要的部件。就其种类而言,通常会根据其使用的冷却剂,将其划分为油浸式变压器与干式变压器[4]。该所研究的是一种以油水为介质的大型输变电设备。一般情况下,电力变压器可以调节电力输送中的电压、电流,保证输送中的电流损失较小,节约经济费用[5]。为保证构建的故障树模型符合实际,对电力变压器的结构进行剖析,如图1所示。
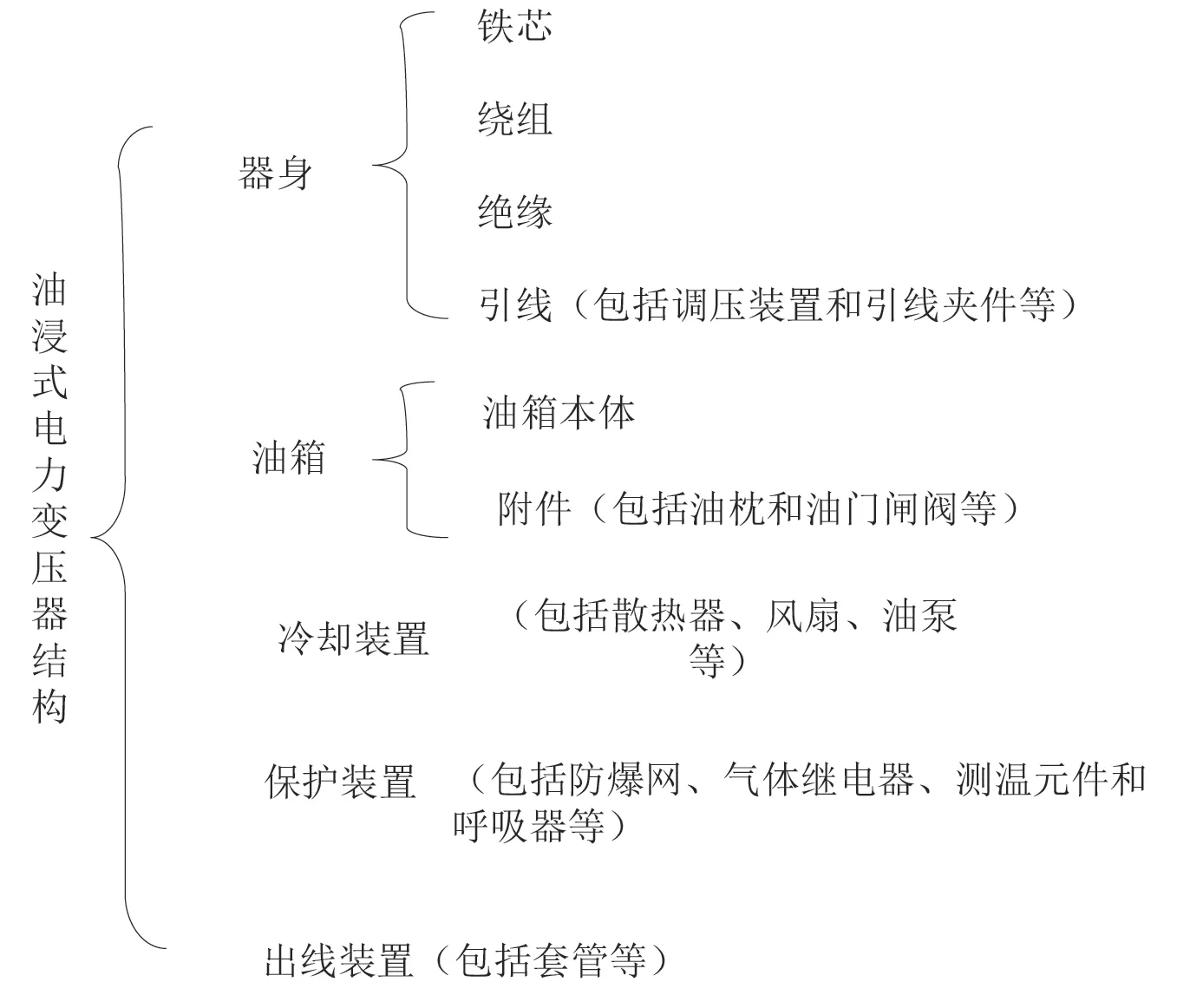
图1 电力变压器的结构
根据故障分析方式,将电力变压器主要故障分为9个种类,见表1。

表1 故障表达方式
将故障形式表示为A1~A9,在此基础上,划分变压器故障树模型中的中间事件、顶层事件、底层事件,建立如图2所示的油浸式电力变压器综合故障树模型。

图2 油浸式电力变压器综合故障树模型
以A1故障、A2故障为例,划分对应的故障树模型子模块,相关内容如图3所示。
图3 设备自身故障模型子模块
参照上述内容,完成油浸式电力变压器综合故障树模型的构建。
3 油浸式电力变压器维修决策
3.1 油浸式电力变压器故障概率计算
在完成对油浸式电力变压器综合故障树模型的构建后,将其作为依据,对油浸式电力变压器故障概率进行计算。在变压器使用的过程中,使用年限不断增加以及在具体操作过程中可能出现的错误操作,都会导致变压器的使用性能下降,其内部各个部件也会出现故障问题[6]。为更好地计算故障发生的概率,将加权法应用到这一过程中,其具体的计算流程如下。
假定当一种故障出现时,在这种故障模式下存在着m个故障特征参量,要想得到故障模式的故障概率,首先要分别得到这些故障参数的故障概率,其次分别与其在设备运行中的权重进行乘以求积,最后将所有故障特征参量的概率相加就可以得到故障模式的故障概率[7]。可以将特定的公式表达如公式(7)所示。
式中:P(Xm)为油浸式电力变压器故障概率。m为变压器在某一种故障模式中的特征参数个数。P(Yi)为某一个故障特征参量出现的概率,i=1,2,……,m。ωi为某一个特征参量在整个故障模式当中的重要性系数,即权重[8]。如果某个特征参数在故障模态中表现正常,那么该参数的权值ω就是0。通过权值的计算,可以得到事故的发生概率,从而得到综合故障的发生概率。
3.2 故障权重划分
当对油浸式电力变压器的不同故障发生时的重要程度进行描述时,借助上述提到的权重ω。在对各项数值进行计算式,结合模糊层次分析法,对不同分层中的方案进行计算,并帮助完成对权重的再次分配。在评价过程中,共设置9个不同标度,其对应的含义也均不相同,9个标度对应基本含义见表2。

表2 9个标度对应基本含义表
表2中A和B均为评价因素。利用一致性检验模糊判断矩阵得到的结果,并对不一致的数据进行校正。在这样的判定中,每一行、每一列所对应的元素,其数值差值均为恒定。该指数是判断模糊评判矩阵是否一致的基础。通常情况下只需要对B=(bij)n×n所对应的行列元素差进行验证,即可判定是否为常数。将各个因素对应的权重代入上述油浸式电力变压器故障概率计算中,根据得到的概率结果完成后续的模糊多属性决策。
3.3 模糊多属性决策
当油浸式电力变压器发生故障时,其产生的部分数据结构清晰,但部分数据结构模糊。针对这些模糊的属性、语言和比重,将其汇总,构成决策集合的模糊参数。模糊指标矩阵的表达如公式(8)所示。
式中:为模糊指标矩阵。针对该模糊指标矩阵,将其与模糊权重指标进行换算,并得到模糊决策指标,如公式(9)所示。
式中:,,…,为变量。为属性比重。根据模糊集合的序列排布方式,对照模糊决策中的变量,从集合当中选取出取值最大结果。具有复杂属性的模糊决策可以通过以下两个步骤来进行操作。首先,计算模糊属性和比重的参数值,并选择有效的算子,将二者进行合理地组合,从而计算方案中最有价值的模糊效应参数。其次,采用模糊排序方法,将各个选项的模糊效应系数进行比较,得到的模糊效应系数最大的就是最满意的选项。采用模糊乐观型决策,这种方法侧重于具体的一种选择,把经济因素作为主要的参考因素,而忽略了其他与此无关或相关性不大的因素。其比例的合理与否,以退化性权值法为基础,而属性参数的取值并不一定是一个唯一的取值,不同的方案所采用的属性参数也不同。
4 结语
在电网中,电力变压器是非常重要的一部分,其具有电能转换和传输的功能,因此,其安全和稳定性对整个电网而言,有非常大的影响。在电力变压器设备中,油浸变压器是最为常见的一种。由于该变电器受工作条件和设备老化等因素的影响,在投产使用后经常会出现故障问题。故障的出现将缩短变压器的使用寿命,但通过对变压器进行适当维护,可以很大程度地提高变压器使用寿命。为增强产品的稳定性和安全性,该文开展了这次研究,对名该确设备故障分析和维护决策,具有十分重要的意义。
经过多年的研发,对变压器的研究不断深入,油浸式变压器的寿命也在逐年增加。关于变压器维护的研究已经取得了丰硕的成果,但仍有许多不足之处。可以在后续的研究中,从变压器风险评价方法上进行创新,不断开发和探索新型风险评估方法,构建更为精确的风险评估模型,以便在今后的变压器运行中,对其状况进行更精准地评估,并对变压器接下来的使用运行情况进行更好地预测。通过建立变压器故障模式与故障树模型,进一步明确变压器故障与其运行之间的关系,在此基础上对变压器进行深入讨论,构建更加详细、完整的细部结构模型,将更多可能的对变压器的安全产生影响的情况都包括在内,以便对变压器故障工况进行及时处理。

