塑性应变能判据在含组合软弱结构面岩质边坡动力稳定分析中的应用
兰 荔,蒋 涛
(1.江西省袁惠渠工程管理局,江西 新余,338000;2.江西省地质环境调查研究院有限公司,江西 南昌,330002)
0 引言
相对于刚体极限平衡法和极限分析法,强度折减法不需要假定滑动面,且边坡岩土体为非均质时仍能适用,因此在边坡的稳定计算中得到广泛的应用[1]。应用强度折减法进行结构稳定分析时,结果的准确性与所选失稳判据关系密切。塑性区贯通、计算不收敛和位移突变判据是目前常用的判据。其中,塑性区贯通无明确客观指标;计算不收敛受迭代次数和迭代容差影响较大;位移突变判据结果与关键点位置关系密切[10]。由于地质构造作用,断层、裂隙及岩层接触面等软弱面往往纵横交错,一处岩质边坡往往在几个软弱结构面的共同作用下发生失稳,其破坏形式与单一软弱结构面的破坏形式有较大差异,尤其是在地震的往复作用下,其稳定性分析十分复杂,需要合适的判据判定其稳定性。考虑到岩土体的破坏过程是塑性区不断发展延伸直至结构失稳的过程,期间伴随着能量的释放和耗散,塑性区应变能表现为先不断增大,然后产生突变,可以通过观察塑性应变能的变化过程来判别结构的稳定状态[10]。张友利等[11]以边坡震后总塑性应变能突变为失稳判别准则对均质边坡在地震作用下的稳定性进行了分析;毕仲辉等[12]基于塑性应变能突变判据对降雨入渗作用下的四川省阿坝州松潘县某岩质边坡稳定进行了分析;李志平等[13]通过构造塑性功与折减系数的尖点突变模型对一阶以及多阶边坡的稳定性进行了分析。但目前还未有学者应用塑性应变能突变判据研究含组合软弱结构面岩质边坡的动力稳定。本文依托于某一实际水利工程设计资料,建立该工程岩质边坡的非线性有限元模型,并在计算中重点考虑断层及岩层层面等软弱结构面的影响,通过建立该含组合软弱结构面岩质边坡震后塑性应变能与折减系数的关系曲线,以塑性应变能突变为判别准则对边坡动力稳定性进行了分析,并将计算结果与常用位移突变、塑性区贯通判据结果进行对比分析。
1 计算理论
1.1 强度折减法
强度折减法固定荷载不变,把边坡现状抗剪强度参数(c、tanφ)等比例折减k 倍,然后用折减之后的边坡抗剪强度参数(c1、tanφ1)进行分析,计算公式如下[14]:
定义边坡达到临界失稳状态时对边坡抗剪强度参数(c、φ)的折减程度k 为安全系数。
1.2 塑性应变能理论
有限元法将结构划分为N 个单元结构,其中第I个单元所拥有的塑性应变能为[10]:
式中:σij、εij分别是单元I 的应力张量和应变张量,VI是单元I 的体积。面设置接触,考虑摩擦力与凝聚力作用,允许接触后分离。具体材料参数见表1。

表1 计算采用的各材料物理力学参数
根据规范反应谱以阻尼比5%,动力放大系数βmax=2.5 拟合了一组水平向峰值加速度为0.2g 和竖向峰值加速度为0.133g 人造地震波[15],地震波持时为20s,如图3 所示。采用粘弹性边界[16]来模拟远域地基辐射阻尼产生的影响。
某一单元结构的塑性应变能发生突变不能表征整个结构的稳定状态,而结构整体塑性应变能的变化过程足以表征结构的稳定状态,将所有塑性变形单元的塑性应变能进行求和得到总塑性应变能E,计算公式为[10]:
2 工程概况及计算模型
某常规水电站为二等大(2)型工程,其泄洪放空洞出口左岸边坡出露的基岩主要为二云石英片岩,岩体破碎,完整性较差,岩层总体产状为NW330°350°/NE∠55°75°。从构造条件来看,主要发育有f12、f13、f11、f14、f9 等5 条小规模断层。边坡采取1:0.3 的坡比进行开挖,最大边坡高度190m。泄洪放空洞出口左岸边坡典型剖面示意图如图1 所示。
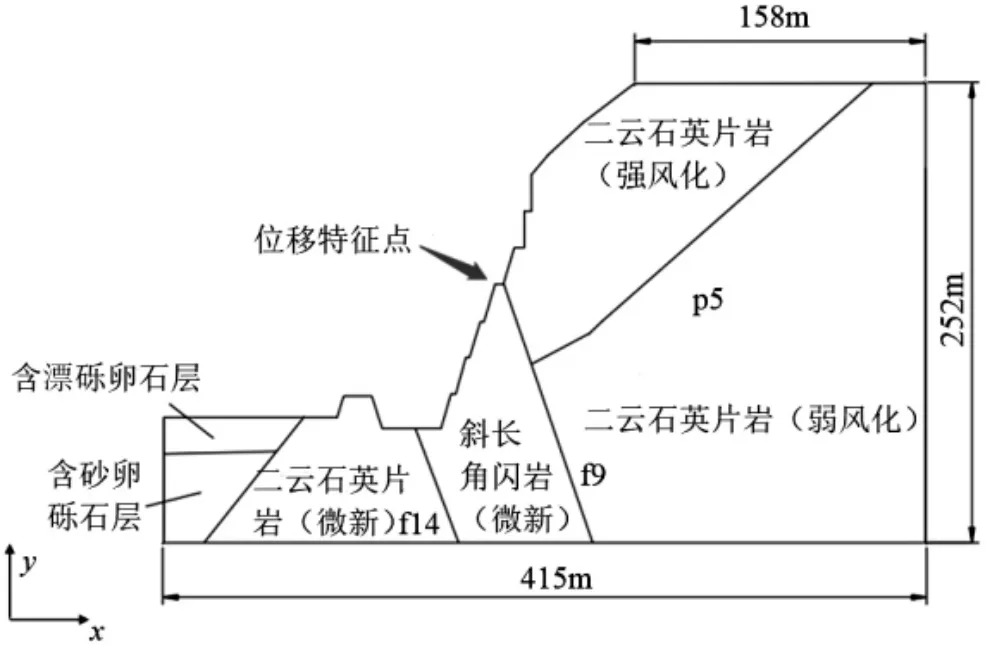
图1 泄洪放空洞左岸边坡典型剖面示意图
按照岩质边坡的材料分区、结构特点等进行网格划分,基于ABAQUS 建立有限元模型,共有节点1585个和单元1467 个。地基深度取62m,边坡向侧面延伸158m。边坡网格划分情况如图2 所示。断层及岩层接触

图2 开挖后泄洪放空洞左岸边坡有限元模型
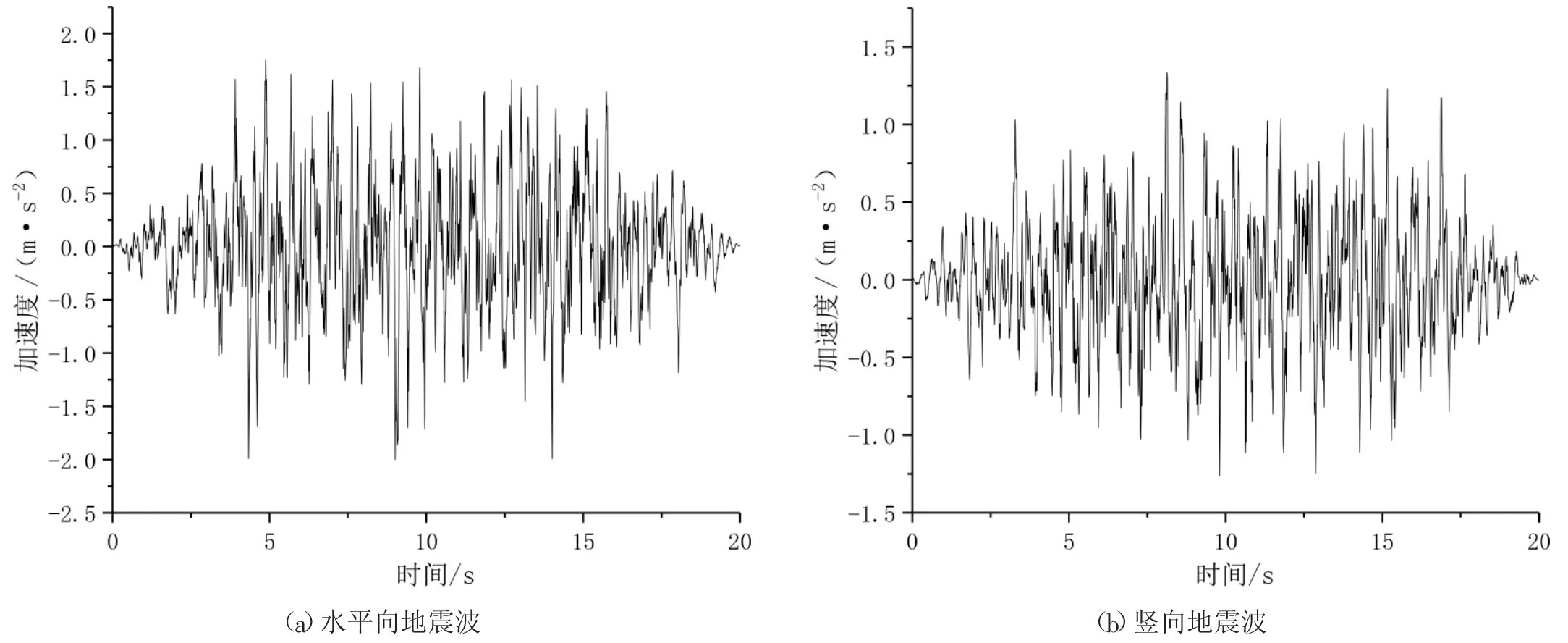
图3 地震加速度时程曲线图
3 结果分析
3.1 塑性应变能突变判据
图4 为折减系数k=2.06 时的边坡塑性应变能随地震动持续时间的关系曲线。从图中可以看出,边坡塑性应变能在随地震动持续时间的增加呈不可逆地增加,提取地震动结束时刻的不同折减系数下的边坡塑性应变能并绘制如图5 所示的关系曲线图。从图中可以看出,边坡震后塑性应变能在折减系数k=2.06 时发生了突变,根据塑性应变能突变判据可以判定,该含组合软弱结构面的岩质边坡的安全系数为2.06。

图4 塑性应变能时程曲线图
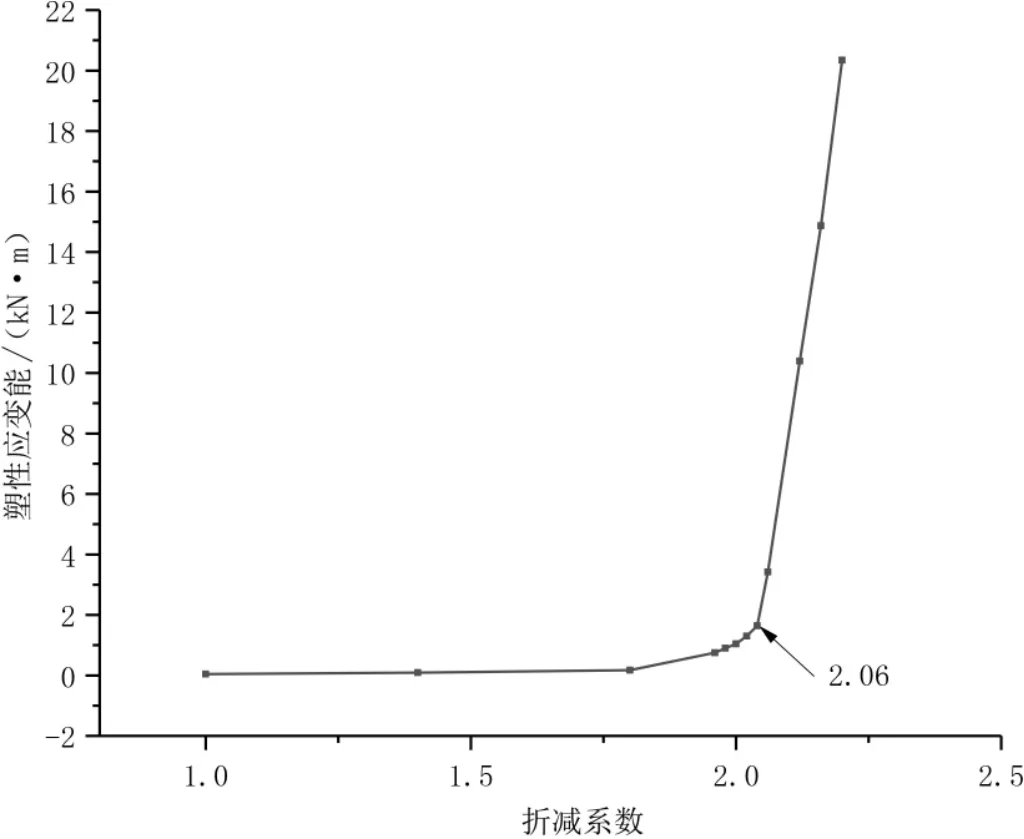
图5 塑性应变能随折减系数变化关系图
3.2 位移突变判据
图6 为折减系数k=2.02 时的边坡特征点位移随地震动持续时间的关系曲线。可以看出,在地震的往复作用下,特征点位移也会随时间发生往复变化,仅以地震发生过程中某一时刻的位移随折减系数的发展情况不足以表征边坡的稳定状态,应以震后残余位移随折减系数的发展情况来判定边坡的稳定状态[17]。提取地震动结束时的不同折减系数下的边坡特征点震后残余位移并绘制如图7 所示的关系曲线图。从图7 中可以看出,边坡特征点残余位移值在折减系数k=2.02 时发生了突变,根据位移突变判据可以判定,该含组合软弱结构面的岩质边坡的安全系数为2.02。

图6 特征点位移时程曲线图
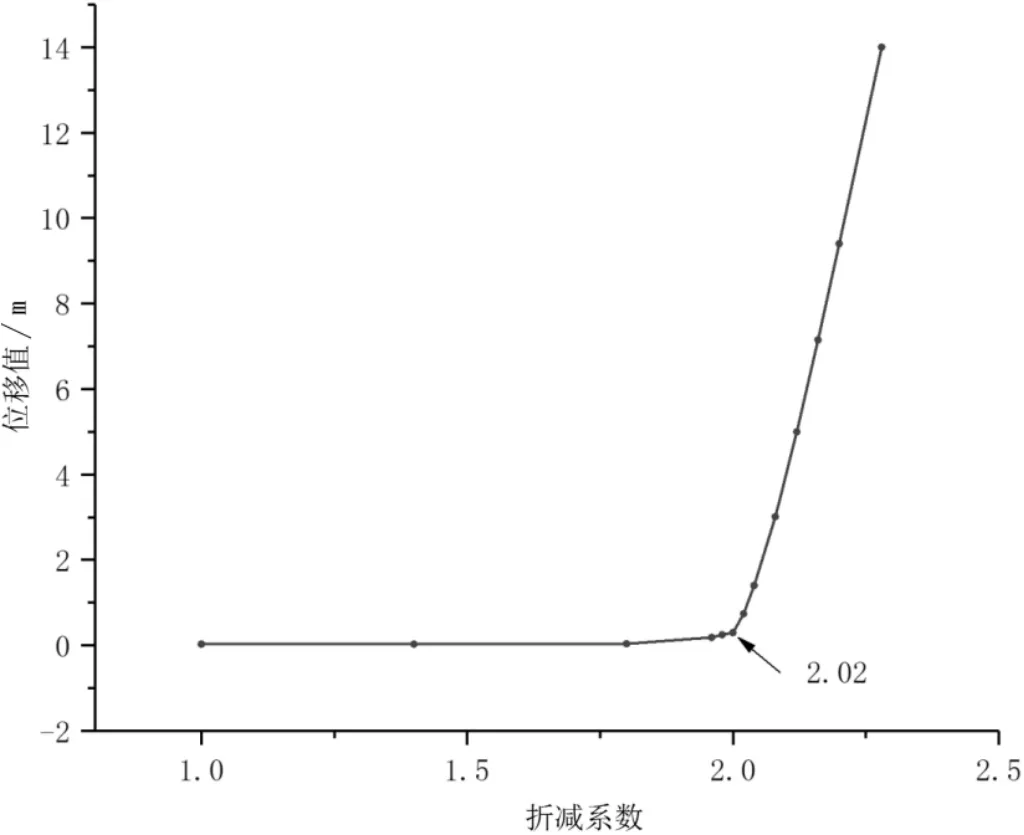
图7 特征点位移值随折减系数变化关系图
3.3 塑性区贯通判据
以上从位移突变的角度对含软弱结构面岩质边坡在地震作用下的稳定性进行了分析,为了佐证以上分析结论的正确性以及更为直观的看到边坡塑性区的发展状态,绘制了边坡在0.2g 地震动作用下对应不同折减系数下的塑性区分布云图,见图8。随着折减系数的增大,岩土材料在不断软化,塑性区从强风化与弱风化的交界面开始产生,之后不断向坡顶以及坡脚进行扩展,当折减系数k=2.05 时,含组合软弱结构面岩质边坡产生了贯通坡顶和坡脚的滑裂面,根据塑性区贯通判据可以判定,边坡在此时发生滑动失稳。

图8 边坡塑性应变区分布云图
3.4 判据汇总对比
将塑性应变能突变判据、特征点位移突变判据以及塑性区贯通判据得到的的结果进行汇总得到表2。从表2 可以看出,根据塑性应变能突变判据得出的该含组合软弱结构面岩质边坡在动力作用下的安全系数为2.06,与根据塑性区贯通判据与特征点位移突变判据得到的结果分别为2.00 和2.02 相差不大,证明了塑性应变能突变判据在含组合软弱结构面岩质边坡动力稳定性分析中的适用性和准确性。

表2 不同判据下的边坡安全系数
4 结论
本文依托于某一实际水利工程设计资料,通过建立该工程含组合软弱结构面岩质边坡震后塑性应变能与折减系数的关系曲线,以震后塑性应变能突变为失稳判别准则对边坡在地震作用下的稳定性进行了分析,并将计算结果与常用特征点位移突变、塑性区贯通判据结果进行对比。主要结论如下:
(1)在含组合软弱结构面岩质边坡动力稳定性分析中,根据塑性应变能突变判据得出的结果与位移突变、塑性区贯通判据得到的结果相近,证明了塑性应变能突变判据在含组合软弱结构面岩质边坡动力稳定性分析中的适用性和准确性。
(2)塑性应变能突变判据以边坡整体塑性应变能这一单值标量为失稳考察量,不会受过多人为因素影响,判定结果唯一,是分析含组合软弱结构面的岩质边坡等受力复杂结构动力稳定性时的较优选择。
(3)本文将含组合软弱结构面岩质边坡的稳定作为平面应变问题进行分析,实际工程中此类边坡的稳定分析十分复杂,在后续研究中可建立组合软弱结构面岩质边坡的三维模型,将塑性应变能突变判据推广到此类边坡的三维稳定分析中。

