考虑电/热需求响应的区域综合能源系统优化调度

薄荣明,蒋 挺,孙立瑶,隋 聪

(1.东北电力大学,吉林 吉林 132012;2.国网通化供电公司,吉林 通化 135000)

0 引言

许多国家正试图调整其能源结构,以减少对传统化石能源的依赖[1-2]。综合能源系统(integrated energy system , IES)的引入为优化能源供应、改善能源效率和生态环境提供了新的方法[3-5]。区域综合能源系统是解决社会能源利用效率低以及可再生清洁能源难以消纳问题的有效途径之一。综合能源系统中多种能量载体可以通过转换、存储和分配满足终端用户的各种能量需求。在此背景下,出现了崭新的商业运营模式,传统的电力供应商发展成为综合能源供应商,能够为能源消费者提供电能、天然气、供热和制冷等[6]。

需求响应(demand response , DR)通过改变终端用户的用能方式削减峰值负荷,分为基于价格的DR和基于激励的DR[7]。DR的概念可以进一步扩展到综合能源系统中,综合需求响应(integrated demand response , IDR)不仅可以调整终端用户耗能的多少,还可以通过能源的价格改变用户耗能的形式[8]。利用不同能源间的互补性,IDR可以提高综合能源系统的可靠性和灵活性[9]。IDR打破了不同形式的能源之间的障碍,使能源用户能够根据不同的能源价格灵活地切换用能方式,例如,用天然气和热能来代替传统的电能,大量的可再生能源可以被进一步利用和再利用[10],进而降低系统的运营成本。

1 综合能源系统模型

1.1 综合能源系统多能流耦合关系

电/气/热多能源系统将不同的能源形式在生产、传输和消费等多个方面进行优势互补。能源中心是以电力系统、燃气系统和热力系统作为典型代表的多能源系统,三者相互耦合、相互关联,无论在多种能源形式的系统中能源耦合形式多么复杂,其都可以简化为3部分,其中包括能源输入、能源输出和多能源系统,见图1。

图1 能源中心输入输出端口

图1中,左侧的P为系统的原始能源输入,右侧的L为需求侧的能源输出。近似数学表达为:

L=f(P)

(1)

式中:f(·)表示多能源系统中各种能源形式的储存、转换、传输和利用等。

由于该系统中的设备只含有能量传输、转换和存储3种,因此可表示为如下关系:

(2)

L=CP

(3)

式中:Le为输出电功率;Lh为输出热功率;Pe为输入电功率;Pg为输入天然气;C为能源耦合矩阵;cij为第i种输入能源与第j种输出能源之间的耦合系数。

内部能量从输入到输出主要分为2个环节,即能源分配和能源转化。能源分配是指能源按特定比例进行能源输送或转化;能源转化是指能源经过能量转换器转换为不同的能源形式,存在一定的能源转换效率。可对式(2)进行进一步的变换:

(4)

式中:ηij为第i种能源与第j种能源之间的转换效率。

进一步表示为:

L=ηNP=CP

(5)

式中:N为分配矩阵;η为效率矩阵。

电/气/热耦合系统可视为一种特殊的能源中心形式,初始输入能源形式有电能和天然气,输出的能源形式有电能和热能,通过电能、天然气和热能的多种能源形式有机结合构成能源中心,实现能源高效利用和满足多类型用户的不同需求。

1.2 综合能源系统能源转换设备模型

1.2.1 CHP机组

热电联产(combined heat and power,CHP)机组的输出功率模型为:

PCHP,e(t)=ηCHP,e·α(t)[Q1·qgas(t)]

(6)

PCHP,h(t)=γCHP,he·PCHP,e(t)

(7)

式中:PCHP,e、PCHP,h分别为机组任意时刻的电、热功率;ηCHP,e为机组的发电效率;α为任意时刻CHP机组的天然气输入比例;Q1为天然气热值,本文取天然气低热值进行计算,其值为35.88 MJ/m3;qgas为任意调度时刻的单位购气量;γCHP,he为机组的热电比,文中的CHP机组采用固定热电比的模式运行。

1.2.2 燃气锅炉

燃气锅炉输出热功率为:

PGB,h(t)=ηGB,h·[1-α(t)]·[Q1·qgas(t)]

(8)

式中:PGB,h为任意时刻燃气锅炉输出热功率;ηGB,h为燃气锅炉的供热效率;1-α为任意时刻燃气锅炉的天然气输入比例。

1.2.3 配电变压器

配电变压器输出的有功功率为:

PT,e(t)=ηT,ePT,grid(t)

(9)

式中:PT,e为任意时刻配电变压器输出的有功功率;ηT,e为配电变压器效率;PT,grid为任意时刻电网侧注入的电功率。

2 电/热负荷综合需求响应模型

电力需求响应是指用户根据价格信号或激励机制做出响应,改变固有用电方式的行为,可分为激励型响应和价格型响应。本文对电负荷构建价格型需求响应模型。同样地,虽然热力负荷也处于终端,但是热负荷不需要像电负荷一样保持绝对的平衡。同时,用户对供热温度舒适度具有一定的模糊性,因此热力负荷可作为一种柔性负荷具有参与调度的价值,基于此,可以在综合能源系统管理中让热负荷参与到调度中。

2.1 电负荷需求响应模型

电能需求体现了电能需求量与电价的关系,即电能需求量与价格的函数关系。需求价格弹性,是用户需求对电价变化的响应程度。根据需求价格弹性,进而分析用户的用电量随电价的变化情况。为了便于描述用电量与电价之间的关系,通常将需求曲线线性化。线性化后,得到用户用电量与电价的函数关系:

(10)

式中:D为电能的需求量;p为电价;ΔD为电能变化量;Δp为电价变化量。

用户在某一时段的用电量与该时段的电价及相邻时段的电价有关。因此,价格弹性分为2种,即自弹性和交叉弹性。需求价格弹性表示负荷变化与电价变化之间的关系,式(11)表示自弹性为电价与相同时段负荷的关系,而式(12)表示交叉弹性为电价与不同时段负荷之间的关系。

(11)

(12)

式中:i,j为不同时间段;hii为自弹性系数(i时段的电量Di与i时段电价pi之间的关系);hij为交叉弹性系数(i时段的电量Di与j时段电价pj之间的关系)。

若Δpi=0,则i时段的hii=0;若Δpj=0,则j时段的hij=0。通常情况下,可采用电量电价弹性矩阵表示用户各个时段的需求响应弹性。选取研究时段总数为n,可以建立n×n维电量电价弹性矩阵。因此,用户的需求弹性表示成矩阵形式:

(13)

响应后用户t时段的用电量:

(14)

2.2 热负荷需求响应模型

热用户对供热舒适度的感知具有一定的模糊性,在一定范围内改变温度值对热用户并没有太大影响,从这方面来讲增加了热负荷的柔性调节能力;另一方面从供热系统热惯性考虑,热网在传输热能过程中具有很大的热惯性。传热介质受比热容和质量的影响,使得受热介质的温度变化在时间上总是滞后于传热介质的温度变化,从热源到用户温度变化的时滞通常为几十分钟到几个小时。

在供热舒适度方面,假设其供暖负荷为室内建筑物采暖,建筑物室内温度可表示为:

(15)

(16)

式中:k=e-Δt/τ。

根据人体舒适度的温度范围,对于室内温度有如下约束:

(17)

式中:Tmin、Tmax分别为人体舒适度可接受的最低室温和最高室温。

式(15)—式(17)共同构成了热负荷需求响应模型,不考虑人的主观意愿影响因素,该模型表明了热负荷可以作为柔性负荷在一定范围内具有可调度价值,即本文提出的热力需求响应。

3 综合能源系统优化调度模型

3.1 目标函数

综合能源系统的优化目标包含CHP机组消耗天然气的成本、燃气锅炉消耗天然气的成本、向电网购电成本、各设备单元的运行维护成本。以一个调度周期为例,通过综合需求响应合理地安排各机组出力,使综合能源系统的收益达到最大。综合能源系统的收益是指其向用户售能所获收入与自身运行成本之差,即:

Rop=Csale-Cbuy-Cop

(18)

式中:Rop为综合能源系统的收益;Csale为综合能源系统售能收入,具体来源于向其他负荷销售电能、热能所获得的收入;Cbuy为综合能源系统从电网公司和天然气公司购能成本,假设在调度周期内购电价格和购气价格是恒定的;Cop为综合能源系统售能的设备运行维护成本,由电运行成本和热运行成本构成。

3.2 约束条件

综合能源系统约束条件由系统能量平衡约束、设备出力约束、设备爬坡约束、配电变压器容量约束等组成。

3.2.1 系统能量平衡约束

综合能源系统向外界供能的电能Pe(t)和热能Ph(t)应与自身各产能设备的输出功率保持实时平衡,即:

(19)

3.2.2 CHP机组出力约束

任意时刻CHP机组应满足功率上下限约束:

(20)

3.2.3 CHP机组爬坡约束

任意时刻CHP机组应满足机组爬坡约束:

(21)

3.2.4 燃气锅炉出力约束

任意时刻燃气锅炉应满足功率上下限约束:

(22)

3.2.5 燃气锅炉爬坡约束

任意时刻燃气锅炉应满足爬坡约束:

(23)

3.2.6 配电变压器容量约束

任意时刻配电变压器应满足最大有功功率约束:

(24)

4 求解算法

对文中所提出的电/热需求响应的综合能源优化调度模型采用粒子群算法求解,求解流程见图2。

图2 模型求解流程

5 算例分析

5.1 基础数据

为了验证模型的有效性,选取我国某地区某一园区综合能源系统。以一天24 h为调度时间,单位调度时间是0.5 h。系统电负荷和热负荷曲线见图3,峰谷平分时电价参数见表1,综合能源系统主要设备参数见表2。电力价格型需求响应自弹性系数取-0.2,交叉弹性系数取0.03,热力需求响应中建筑物的热阻均取18° C/kW,建筑物的室内最佳温度是21 ℃,最低温度是18 ℃,最高温度是24 ℃,电价为0.4元/kWh,天然气价格为2.5元/m3。

表1 峰谷平分时电价参数

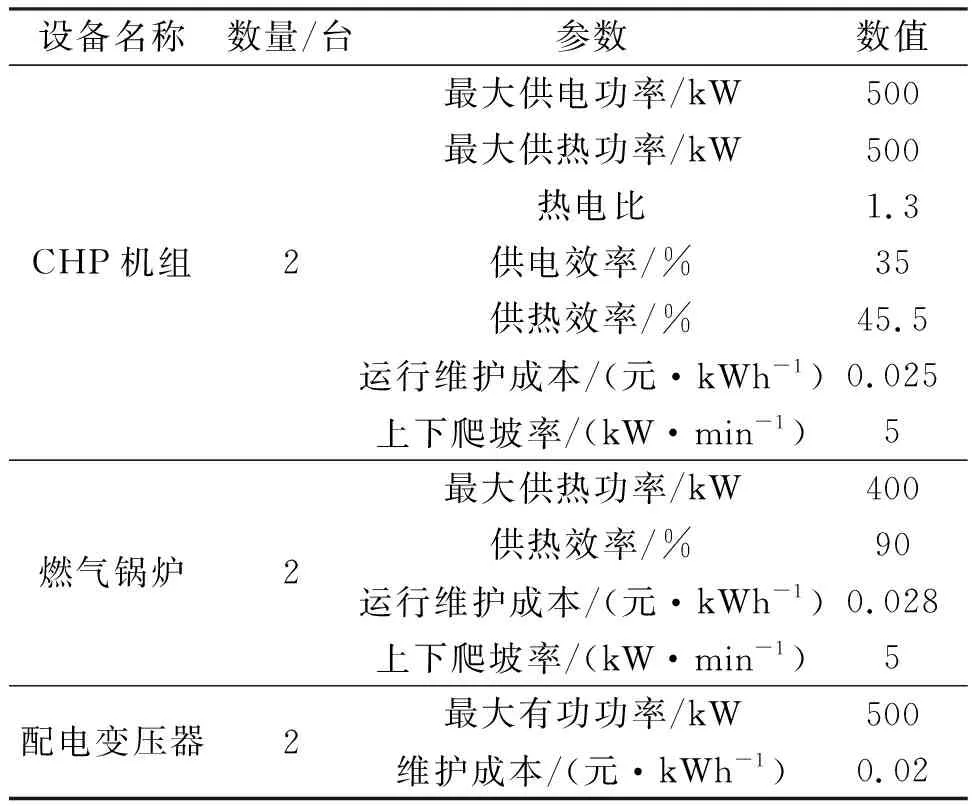
表2 综合能源运营商主要设备参数

图3 电/热负荷预测曲线

5.2 仿真结果

基于已建立的需求响应模型和综合能源运行优化模型进行仿真分析。仿真过程中进行负荷响应和调节,综合能源系统收益最大为优化目标,为了验证该系统考虑电/热多种负荷综合需求响应的优势,设置了以下几种场景方案进行对比。

1) 方式1:未考虑综合需求响应。

2) 方式2:仅考虑了电负荷需求侧响应。

3) 方式3:仅考虑了热负荷需求侧响应。

4) 方式4:考虑了电力与热力综合需求响应。

不同运行方式下需求响应侧电负荷优化曲线见图4,不同运行方式下需求侧热负荷的优化曲线见图5。

图4 不同运行方式下需求响应侧电负荷优化曲线

图5 不同运行方式下需求侧热负荷的优化曲线

从图4和图5中可以看出,在综合能源管理中,考虑多种负荷综合需求响应比未实行需求响应以及实行电负荷需求响应或实行热负荷需求响应的单一负荷需求响应起到更好的削峰填谷作用,更有效地降低了峰谷差。

不同运行方式下CHP机组电出力曲线见图6,不同运行方式下CHP机组热出力曲线见图7。

图6 不同运行方式下CHP机组电出力曲线

图7 不同运行方式下CHP机组热出力曲线

从图6与图7中可以看出,运行方式4中CHP机组的电出力和热出力比较平稳,波动较小,在2～10时段,未考虑需求响应时CHP机组出力波动较大,其机组灵活性较低,考虑综合需求响应,电力负荷受价格型需求响应的影响以及热力负荷受供热传输延迟和供热舒适度模糊性的影响,能够有效提高CHP机组的灵活性。

不同运行方式下综合能源系统运行成本、购能成本、售能收入见表3。

表3 不同运行方式下综合能源系统经济性对比 单位:元

从表3看出,未实行需求响应时,综合能源系统运行成本为8 550.538元,实行综合需求响应系统后运行成本为7 940.228元,运行成本有所下降。未实行需求响应时,综合能源系统购能成本为5 411.612元,实行综合需求响应后系统购能成本为4 895.399元,购能成本有所下降。综合需求响应的应用提高了区域综合能源系统电/热生产的灵活性,考虑电/热多种负荷综合需求响应相比于单一考虑需求响应,可有效地降低需求侧用户的总能源消耗成本以及系统的运行成本。

6 结论

随着电/热负荷日益联系密切,在综合能源管理中热力负荷同样也具有可调度价值。针对现有研究较少考虑需求侧各类负荷的可调度性的情况,基于电力需求侧响应在削峰填谷、消纳新能源方面起到了重要的作用,在电力负荷价格型需求响应的基础上,根据热力负荷在传输时具有延迟性以及热用户对供热舒适度具有模糊性的特点,可以将热力负荷作为柔性负荷参与到优化调度中,建立了热力负荷需求响应模型。在综合能源系统优化时,综合考虑电负荷与热负荷间的优势互补,提高能源利用效率,协调网内电源优化,使CHP机组更加灵活地运行,节约了综合能源系统能源消耗成本。