平抑风光功率波动的混合储能功率分配策略

黄利祥, 张新燕, 梁帅, 施锐, 廖世强, 张光昊

(新疆大学电气工程学院, 乌鲁木齐 830017)

微电网的产生,一定程度上增强了电网对分布式风电、光伏的接纳能力[1]。由于风光出力存在随机性、波动性和间歇性,直接并网会导致电网的安全稳定运行遭受影响[2]。

通过在风电、光伏系统中配置储能系统,可有效平抑风光输出功率波动[3],提升微电网并网运行能力和电力系统的稳定性。储能装置包括能量型和功率型[4],能量型储能的代表有:抽水蓄能、蓄电池、全钒液流电池等,其能量密度较大,功率密度较小,且循环寿命较短,不宜频繁充放电;功率型储能以超级电容、超导储能和飞轮储能等为代表,能量密度较小,功率密度较大,频繁充放电不会损害其性能。由于单类型的储能难以同时满足功率和能量的需求,因此采用功率型和能量型组成的混合储能系统(hybrid energy storage system, HESS)弥补单一储能装置的不足,延长储能元件的使用寿命,提高电力系统运行经济性[5],还能快速充放电,使风光波动功率得到有效平抑。由于全钒液流电池安全性高、充放电持续时间长,是能量型储能的代表;超级电容使用寿命长、响应速度快,是功率型储能的代表[6],因此选用全钒液流电池和超级电容构成混合储能系统。

为了充分发挥能量型储能和功率型储能的优势互补,对混合储能系统进行合理的功率分配是当前研究的热点。关于混合储能功率分配策略的研究,国内外学者常用的方法有:低通滤波、小波变换、小波包分解和经验模态分解(empirical mode decomposition,EMD)等[7]。文献[8-9]利用低通滤波算法对混合储能系统进行功率分配,但其滤波过程存在时间延迟,影响功率分配结果的准确性。文献[10]采用一种基于小波变换的功率分配方法合理划分高低频分量,但小波基的选取和分解层数关系到小波变换的结果。文献[11]直接将原始风电功率用小波包分解,所得低频信号用于并网,再通过HESS平抑中高频功率信号,但小波包分解的结果受基波影响。文献[12]采用EMD与希尔伯特相结合的方法分析间歇性负荷的频域特性,从而确定蓄电池和超级电容各自响应的部分信号,但EMD在分解过程中存在严重的模态混叠现象和端点效应问题。由Dragomiretskiy等[13]提出的变分模态分解算法(variational mode decomposition, VMD)可以自适应地确定各模态分量对应的中心频率和带宽,实现信号的准确分离,克服了采用EMD分解信号产生的模态混叠现象[14],广泛应用于信号分析领域。文献[3]为使得风光出力平滑并网,采用VMD分解风光波动功率信号,实现HESS功率合理分配,但主观确定VMD分解模态数K和惩罚因子α可能导致信号分解不合理,此外,直接忽略了VMD分解剩余量中可能含有的重要信息,影响风光输出功率的平抑效果,不利于微电网可靠并网。

综上所述,考虑到VMD算法人为确定参数以及忽略其分解余量影响所存在的不足,现针对微电网中风光输出有功功率波动问题,提出一种基于鲸鱼优化算法(whale optimization algorithm, WOA)优化VMD参数K和α,并考虑其分解余量的混合储能改进功率分配策略。首先,利用移动平均算法选取合适的滑动窗口长度,得到符合国家风光并网标准的并网功率,计算出混合储能系统待平抑的风光波动功率;然后,确定鲸鱼算法的适应度函数,完成VMD参数K和α的寻优过程,将得到的最佳参数K和α代入VMD算法分解风光波动功率,得到一系列按中心频率从低到高排列的固有模态分量(intrinsic mode functions,IMF)和分解余量RES,再对RES进行VMD分解,得到第二组模态分量imf和分解余量res,再根据不同类型储能的特性,完成HESS的初级功率分配;最后,考虑到超级电容容量较小,为避免其过度充放电,利用模糊控制进行功率二次分配,优化储能荷电状态(state of charge,SOC)维持在安全范围。

1 鲸鱼算法优化VMD参数

1.1 VMD算法原理

变分模态分解(VMD)算法首先通过构造变分模型,预设模态分解数K和二次惩罚因子α,然后迭代搜寻模型的最优解,自适应分离各模态分量IMF。算法分解的本质是维纳滤波降噪,每个IMF都可以作为调频-调幅信号,表达式为

uk(t)=Ak(t)cos[φk(t)]

(1)

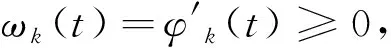
步骤1VMD变分模型构造。将初始信号f分解为K个IMF分量uk(t),各uk(t)都有相应的带宽和中心频率,使带宽和最小,约束条件设为各uk(t)的和等于f,表达式为

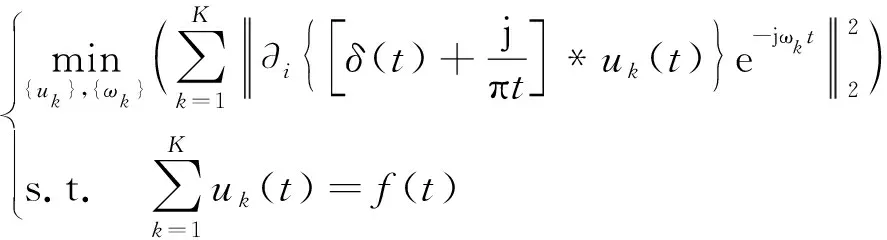
(2)

式(2)中:*为卷积运算;{uk}={u1,u2,…,uk}为全部IMF分量;{ωk}={ω1,ω2,…,ωk}为各IMF对应中心频率;δ(t)为单位冲激函数。

步骤2VMD变分模型求解。首先将约束变分模型转换为非约束变分模型,增设拉格朗日(Lagrange)乘子λ,构造函数为

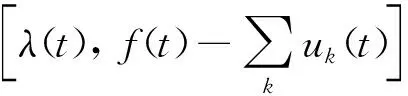
(3)

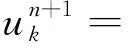
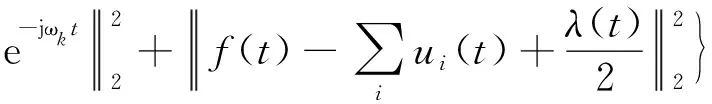
(4)

将式(4)通过Parseval/plancherel变换到频域,可得

(5)

将式(5)改写成非负频域的半空间积分,可得

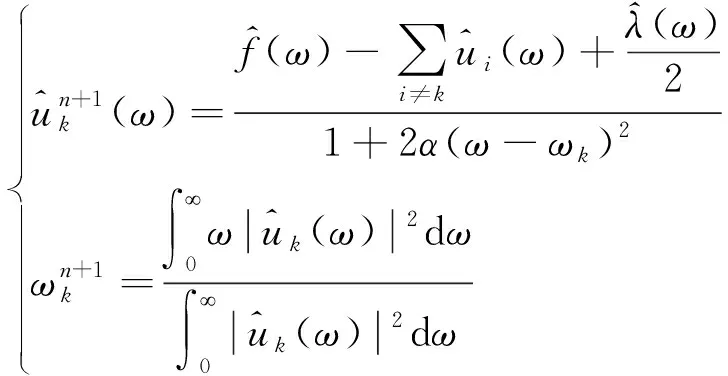
(6)

1.2 鲸鱼优化算法

鲸鱼优化算法(WOA)最大的特点就是利用随机个体或者最优个体来模拟座头鲸的捕食行为。对比粒子群算法、遗传算法等方法,WOA具有简单易实现、参数少、寻优速度快、全局收敛性强且优化精度高等优点。鲸鱼捕食分3个阶段进行。

第一阶段:包围猎物捕食。这个过程中鲸鱼位置更新的数学模型为

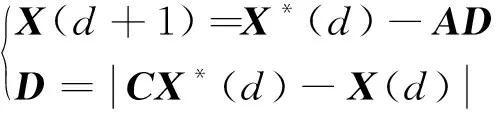
(7)

式(7)中:d为迭代次数;X(d)为鲸鱼位置;X*(d)为最优鲸鱼位置;D为鲸鱼个体到最优位置的距离;AD为包围猎物时的移动步长;A、C为系数矩阵,矩阵中元素的计算公式如式(8)所示。

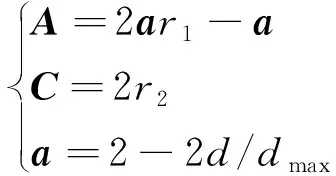
(8)

式(8)中:dmax为最高迭代次数;a代表收敛因子;r1和r2在[0,1]上随机分布。

第二阶段:螺旋搜索气泡捕食。此过程对应的数学模型为

(9)

式(9)中:b为螺旋形常数;D′为鲸鱼种群到最优位置的距离;l为[-1,1]随机分布的常数。

由于鲸鱼在螺旋上升搜寻猎物的同时会缩小包围圈,假定鲸鱼执行上述两种捕食行为的概率均为50%,为了保证两个动作能够同时进行,引入[0,1]上随机分布的数p。更新后的鲸鱼位置为

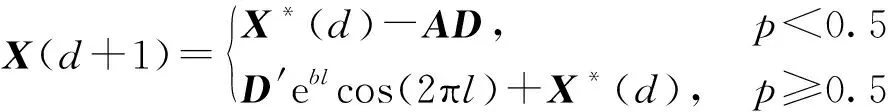
(10)

第三阶段:随机搜索捕食。若|A|<1,表明该鲸鱼采用螺旋包围方式搜索猎物,其数学模型如式(10)所示;反之,若|A|≥1,表明该鲸鱼随机搜索猎物,对应数学模型为

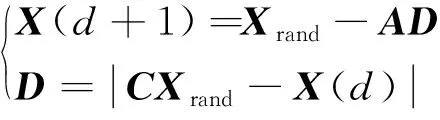
(11)

式(11)中:Xrand为一个随机的鲸鱼位置向量。

最后,将鲸鱼捕食的3个阶段相结合便构成鲸鱼优化算法。

1.3 WOA优化VMD参数

VMD的分解效果取决于模态数K和惩罚因子α的大小。在进行传统的VMD分解之前,需要预设参数K和α,合适的K、α值可以提升信号分解的效果。

最初有关VMD的研究中,众多学者利用中心频率观察法,对比不同K值下各IMF中心频率的分布情况人为确定合适的K值,这种方式主观性较强,且无法确定α的取值。后来便有学者提出利用粒子群算法、遗传算法等方法优化VMD参数K和α,提升其分解效果。目前有关VMD参数优化尚未统一理论,更没有最好的方案。以包络熵[15]极小值作为WOA的适应度函数优化VMD参数[K,α],建立WOA-VMD参数优化模型。包络熵的大小决定了原信号特征信息的多少,包络熵值越大,表明原信号中无用信息较多,反之,包络熵值越小,表明特征信息较多[16]。WOA优化VMD参数设置如表1所示,算法步骤流程如图1所示。包络熵的数学模型为

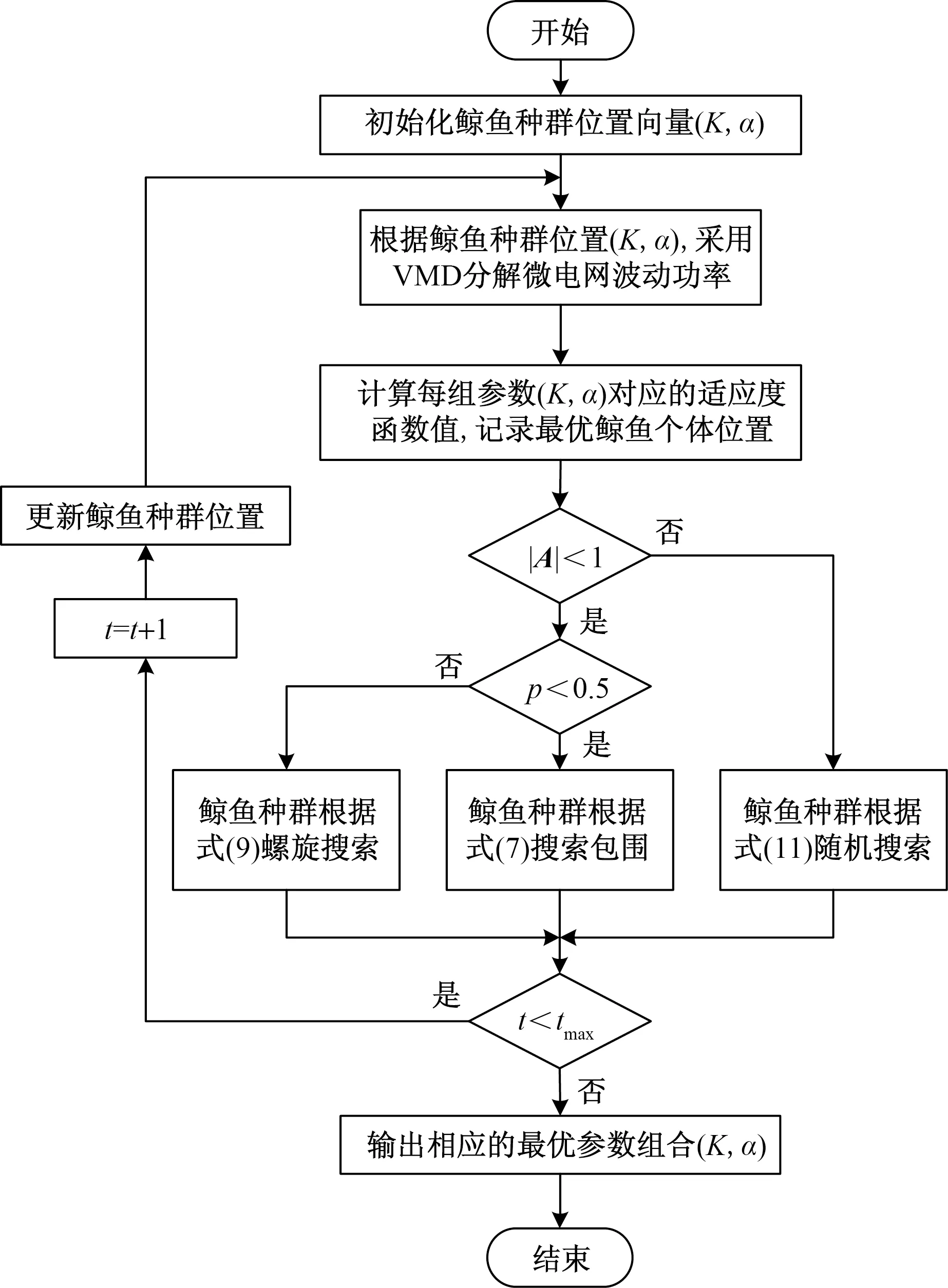
图1 WOA优化VMD参数流程Fig.1 WOA process for optimizing VMD parameters

表1 WOA优化VMD的参数设置Table 1 WOA optimized VMD parameter settings

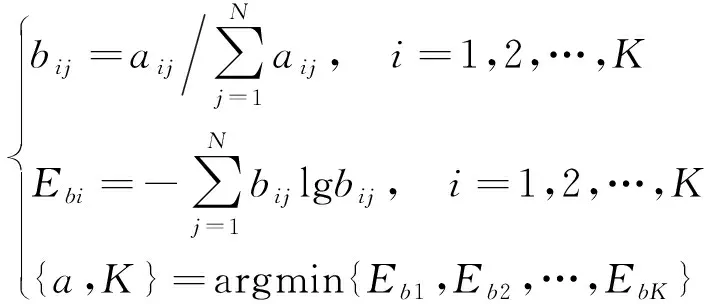
(12)

式(12)中:N为信号采样点数;K为模态分量的个数;aij为各模态分量经调制后得到的包络信号;aij经归一化处理后得到bij,计算其熵值即为包络熵Ebi。

2 风光互补HESS功率分配策略

2.1 风光波动功率

以并网型风光互补发电系统作为研究对象。为了使风光输出功率波动得到有效平抑,保证微电网系统可靠并网,持续稳定地提供电能,需增设全钒液流电池和超级电容器组成的HESS,充分利用二者的优点,提升储能系统的性能。风光互补并网结构如图2所示。

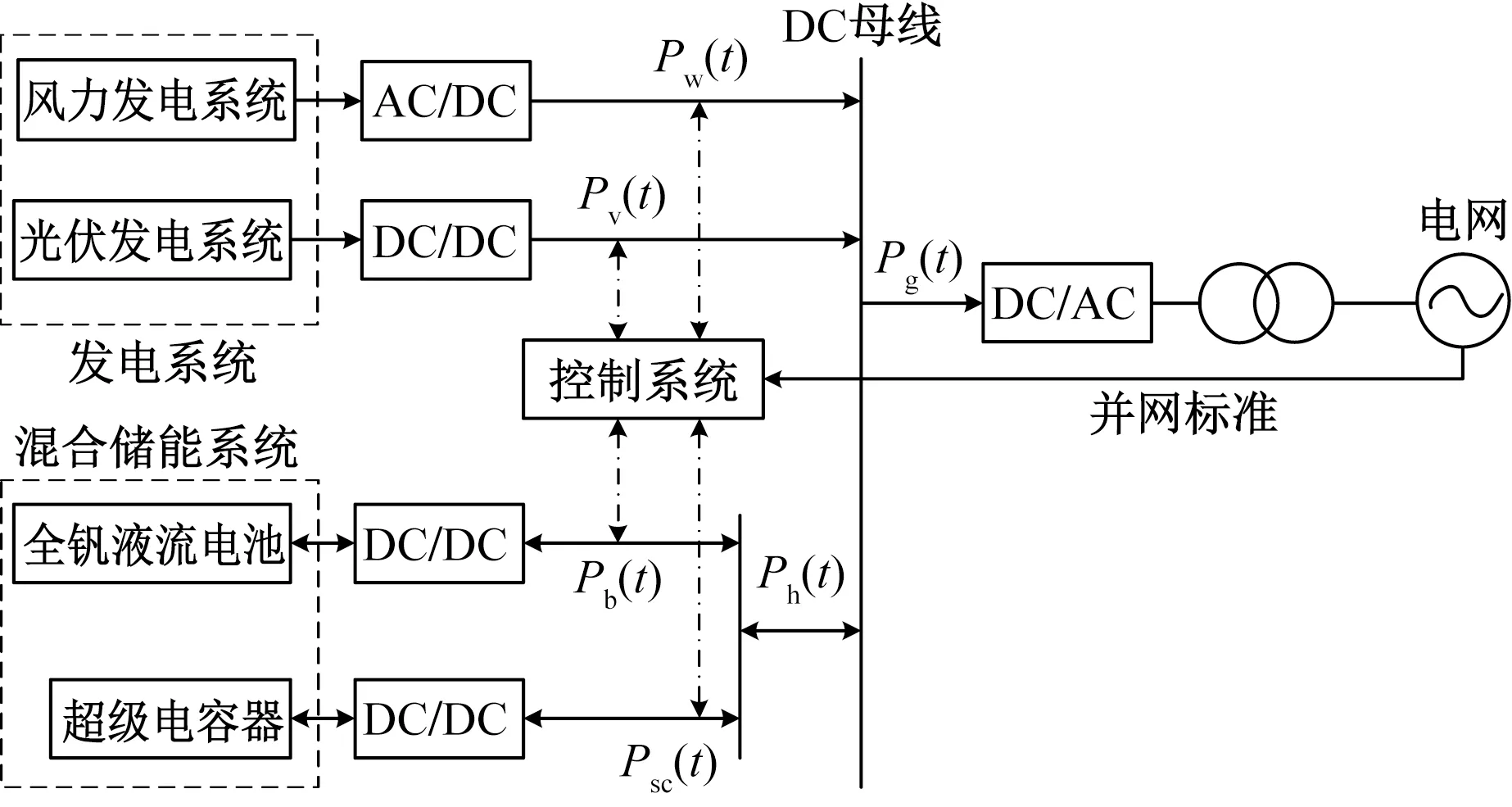
Pw(t)、Pv(t)分别为风电、光伏输出有功功率;Pg(t)为并网功率;Ph(t)为HESS参考功率;Pb(t)为全钒液流电池吞吐功率;Psc(t)为超级电容吞吐功率图2 风光互补并网结构Fig.2 Grid-connected structure of solar wind

图2中,Ph(t)即为待平抑的风光出力波动功率,数学模型对应式(13)。规定Ph(t)>0时,HESS充电;Ph(t)<0时,HESS放电。

Ph(t)=Pw(t)+Pv(t)-Pg(t)

(13)

关于并网功率Pg(t)的获取,现有研究中使用较多的是利用EMD、VMD、小波分析、小波包分解等方法直接对原始风光功率信号进行分解,将得到的低频信号作为并网功率信号,这样可能导致风光功率平抑不足或者过平抑的现象。因此,根据我国风电和光伏并网标准[17-18],利用移动平均滤波算法选取适当的窗口长度L,得到符合要求的并网功率Pg(t),再根据式(13)计算出HESS的参考功率Ph(t),该方法可有效避免波动功率平抑不足或者过平抑现象。移动平均算法流程如图3所示。

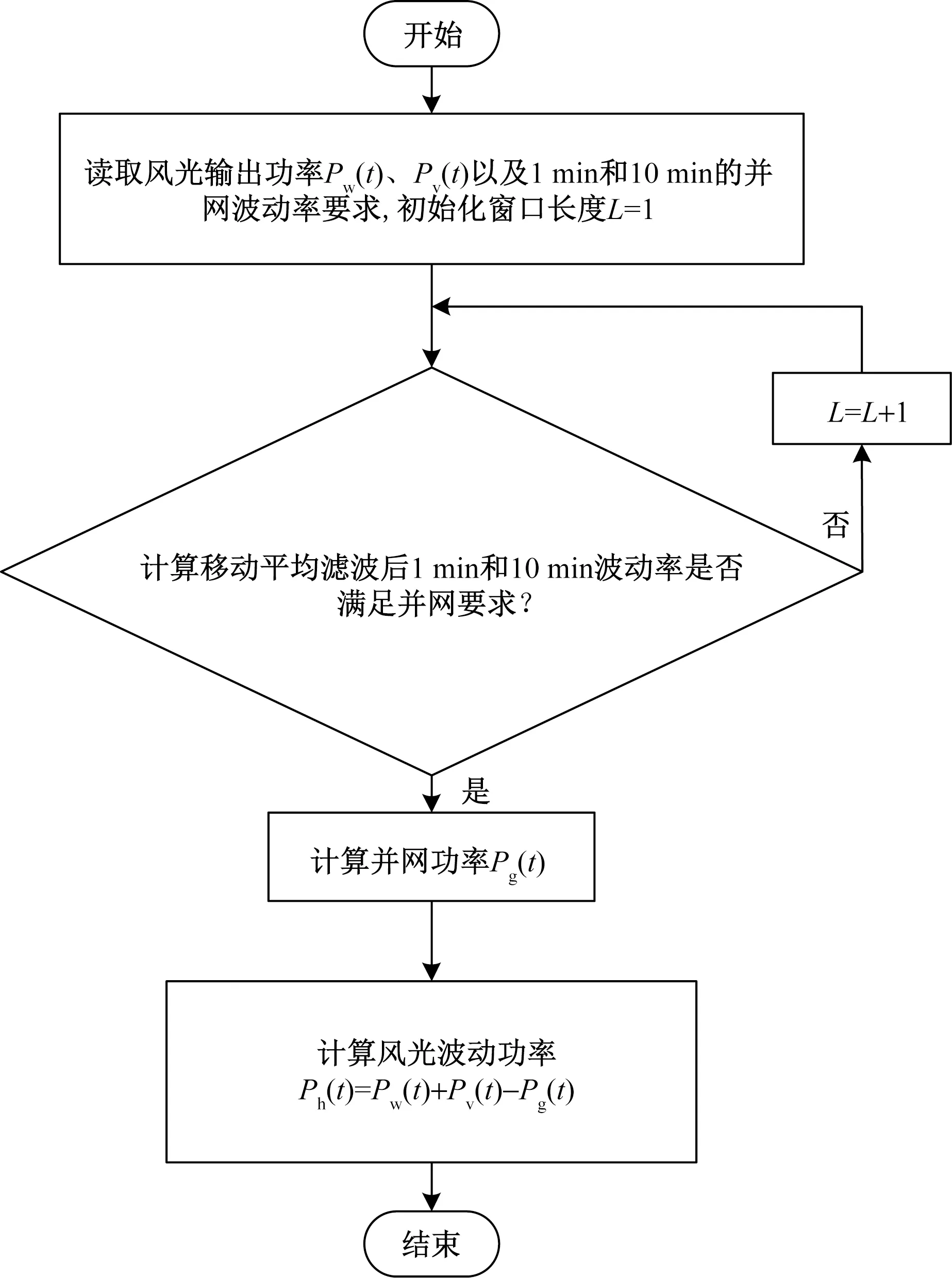
图3 移动平均算法流程Fig.3 The flow of moving average algorithm

2.2 基于WOA-VMD双层分解的改进功率分配策略

采用WOA-VMD算法将HESS的参考功率Ph(t)自适应地分解为一系列按频率由低到高排列的K个模态分量IMF和分解余量RES,再对RES进一步分解,得到k个模态分量imf和余量res。在以往的研究中,全钒液流电池和超级电容器功率分配的合理性取决于各IMF分量的高低频划分界限,没有考虑VMD分解后剩余量RES中可能包含的丰富信息,直接忽略了剩余分量的影响,这样可能导致HESS的配置容量偏小,波动功率平抑不足,甚至加快储能装置的充放电频率,缩短其使用寿命。因此,提出在WOA-VMD分解风光波动功率的基础上,充分考虑分解余量RES中包含的丰富信息,再次利用VMD对RES进行分解,然后分别对VMD分解风光波动功率得到的各模态分量IMF和分解RES得到的各模态分量imf进行频谱分析,完成HESS的初级功率分配。根据首次VMD分解所得IMF的混叠程度,确定高低频率分界点,对应的频率值作为第二次VMD分解所得imf的高低频率划分依据,将两次VMD分解产生的高低频信号分别重构后依次分配给超级电容和全钒液流电池。此外,第二次VMD分解仍然会有些许剩余量res,包含全频段的功率信息,考虑到应尽可能减少电池的充放电频率,延长其寿命,因此,将第二次VMD分解产生的余量res充当高频分量分配给超级电容器。

采用VMD分解的混合储能传统功率分配策略对应的数学模型如式(14)所示。

(14)

改进功率分配策略对应的数学模型为

(15)

式中:M、m分别为两次VMD分解后的高低频分界点;K、k分别为两次VMD分解产生的模态分量数;N、n分别为第N个IMF分量和第n个imf分量;res为第二次VMD分解产生的剩余量;Pbat1、Psc1分别为采用传统初级功率分配策略分配给全钒液流电池和超级电容的功率指令;Pbat、Psc分别为采用初级功率分配策略分配给全钒液流电池和超级电容的功率指令。

2.3 基于模糊控制的混合储能功率二次分配

由于超级电容等功率型储能容量较小,在充放电过程中容量很容易达到额定值,超出安全充放电范围,难以有效平抑风光输出功率波动。因此,有必要将超级电容的剩余容量控制在一定范围内。通常用荷电状态(SOC)描述储能装置的剩余容量,超级电容充放电时对应的SOC数学模型如下。

(16)

式(16)中:Psc(t)为t时段结束时超级电容的功率,Psc(t)>0表示充电,Psc(t)<0表示放电;SOCsc(t)、SOCsc(t-1)分别为t时段和t-1时段结束时超级电容的SOC;Δt为时段长度;ρsc为超级电容的自放电率;Esc表示超级电容额定容量;ηc、ηd分别为超级电容的充放电效率。

利用模糊控制的方法对超级电容的SOC进行自适应控制,避免其出现过充过放现象。当SOCsc(t)适中时,超级电容按照初始功率指令进行充放电;当SOCsc(t)较小时,若此时超级电容处于放电状态,则须分配部分功率指令给全钒液流电池承担,避免出现过放现象,若处于充电状态,则无须进行调整;同理,当SOCsc(t)较大时,若此时超级电容处于放电状态,则无须进行调整,反之,若处于充电状态,则须分配部分功率指令给全钒液流电池承担,避免出现过充现象。

控制器选用双输入单输出的模糊控制器,输入、输出隶属度函数选择常用的三角形和梯形隶属函数,反模糊化采用重心法。输入一为t-1时段结束时超级电容的荷电状态SOCsc(t-1),模糊论域为[0,1],模糊集为{VS,S,M,B,VB },对应超级电容SOC为{很小,小,中,大,很大};输入二为t时段超级电容SOC变化量Dsc(t),模糊论域为[-1,1],模糊集为{NB,NM,NS,PS,PM,PB},分别表示超级电容SOC的变化为{负多,负中,负少,正少,正中,正多};输出为t时段超级电容的功率调整系数Ksc(t),模糊论域为[0,1],模糊集为{VS,S,MS,MB,B,VB},分别对应Ksc(t){很小,小,较小,较大,大,很大}。模糊控制的输入、输出隶属度函数和模糊规则分别如图4和表2所示。

图4 模糊控制的输入输出隶属度函数Fig.4 Input and output membership functions of fuzzy control

表2 模糊控制规则Table 2 Fuzzy control rule

经模糊控制优化后,超级电容和全钒液流电池的功率如式(17)所示。

(17)

3 算例分析

以新疆哈密地区微电网(风电额定功率300 kW,光伏额定功率200 kW)某天(1 440 min)的实际有功输出作为风电、光伏出力曲线,采样时间间隔1 min。采用全钒液流电池和超级电容器构成HESS平抑风光功率波动。相关参数如表3所示。

表3 混合储能系统相关参数Table 3 Related parameters of hybrid energy storage system

为满足中国风光并网标准[17-18],采用移动平均滤波平滑风光输出功率,确定并网功率Pg(t),由式(13)计算HESS参考功率Ph(t)。图5为初始风光功率和平抑后的并网功率曲线;图6、图7分别表示移动平均前后1 min和10 min的功率波动率,符合国家标准;图8为风光波动功率。

图5 风光功率和并网功率Fig.5 Wind-PV power and grid-connected power

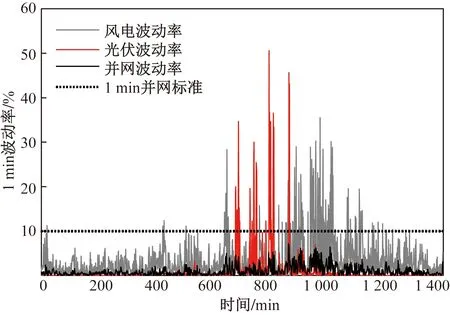
图6 平抑前后1 min波动率Fig.6 The fluctuation rate of 1 min before and after suppression

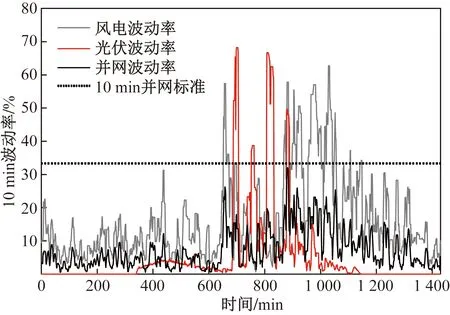
图7 平抑前后10 min波动率Fig.7 The fluctuation rate of 10 min before and after suppression

图8 风光波动功率Fig.8 The fluctuation power of wind-PV

为了验证WOA优化VMD参数的优势,与遗传算法(GA)优化VMD参数进行对比,图9为两种算法的迭代寻优过程。显然WOA在第8次迭代时获得最小适应度函数值9.615 7,而GA的最小适应度函数值9.616出现在第14次迭代。迭代寻优结果表明,WOA相对于GA而言,其寻优速度快且计算精度高。

为了验证VMD分解信号的优势,分别采用VMD和EMD分解Ph(t),将产生的IMF作频域分析,观察模态间的混叠程度。WOA优化VMD所得最优参数组合[K,α]=[8,2 653],Ph经VMD分解后的8个IMF分量和余量RES如图10所示,将图10中的各IMF作频域变换,得到图11所示频谱。观察图11可知,各IMF的特征频率易于分辨。Ph经EMD分解后,再经FFT变换到频域如图12所示,各IMF混叠现象尤为明显, IMF1几乎分布于全频段,高低频分量较难区分。因此VMD对比EMD,更便于观察各IMF的混叠程度,确定高低频分界点,完成HESS功率的合理分配。

图10 波动功率经VMD分解后的结果Fig.10 The result of VMD decomposition of fluctuating power

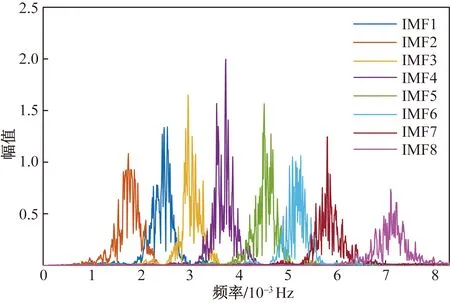
图11 经VMD分解后的各IMF对应频谱Fig.11 The corresponding spectrum of each IMF after VMD decomposition

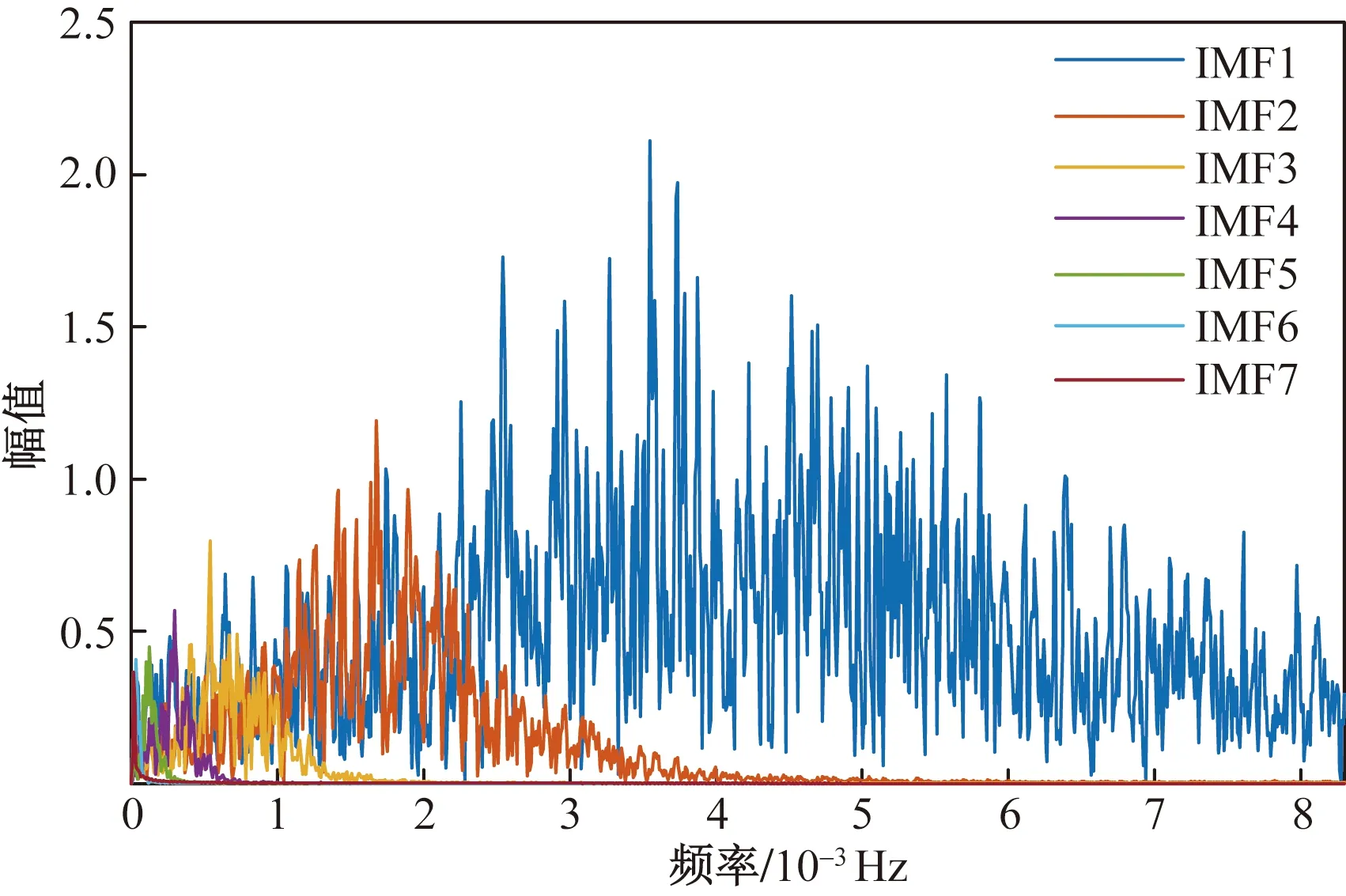
图12 经EMD分解后的各IMF对应频谱Fig.12 The corresponding spectrum of each IMF after EMD decomposition

从图10可以看出,余量RES中仍包含重要信息,再次利用WOA-VMD分解RES,得到如图13所示的7个imf分量和余量res,此时res中仅包含少量信息,对imf作频域变换得到图14所示频谱。

图13 RES经VMD分解后的结果Fig.13 The result of VMD decomposition of RES

图14 各imf对应频谱Fig.14 Each imf corresponds to the spectrum

根据图11中各模态的混叠程度可知,IMF7与IMF8之间的模态混叠尤为轻微,确定分界点处的频率为6.5×10-3Hz,作为imf的高低频判断依据。将IMF1～IMF7和imf1～imf5作为低频功率信号分配给全钒液流电池,IMF8和imf6、imf7以及res作为高频功率信号分配给超级电容,初步完成HESS的功率分配。利用所提改进功率分配策略对比传统功率分配策略所得全钒液流电池和超级电容的功率曲线分别如图15和图16所示。

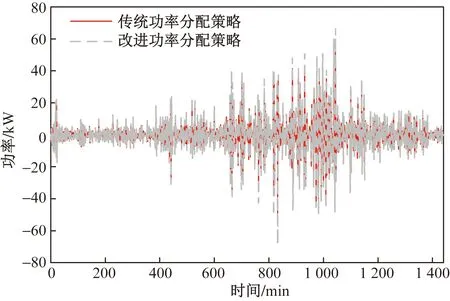
图15 全钒液流电池功率曲线Fig.15 Power curve of all vanadium flow cell

图16 超级电容功率曲线Fig.16 Power curve of the supercapacitor

为避免超级电容SOC越限,对HESS功率的初级分配经模糊控制进行修正。图17和图18分别对比了模糊控制前后全钒液流电池和超级电容的SOC变换情况;图19为模糊控制后的HESS功率曲线。

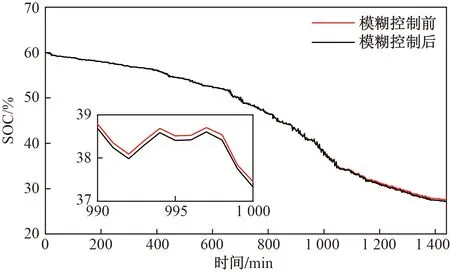
图17 全钒液流电池SOCFig.17 All-vanadium liquid flow battery SOC

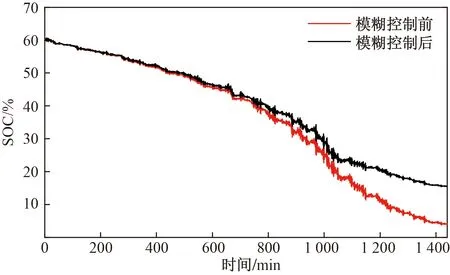
图18 超级电容器SOCFig.18 The SOC of the supercapacitor

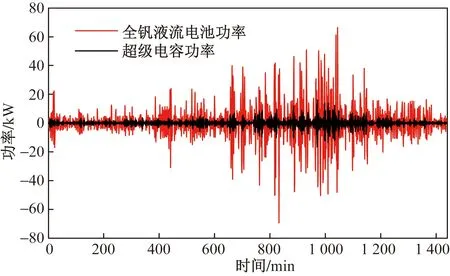
图19 二次分配后HESS功率曲线Fig.19 HESS power curve after secondary distribution

分析图17和图18可以得出全钒液流电池和超级电容SOC变换情况,如表4所示。全钒液流电池的SOC经模糊控制前后均处于20%～80%的合理范围;超级电容的SOC经模糊控制后从3.7%～60.7%变为15.4%～60.6%。结果表明超级电容经模糊控制优化后的SOC可以维持在合理范围内,避免了过度充放电现象。

表4 模糊控制前后SOC变化范围Table 4 Variation range of SOC before and after fuzzy control

4 结论

针对风电、光伏输出有功功率波动问题,以超级电容器和全钒液流电池构成HESS作为研究对象,提出一种基于WOA-VMD双层分解的改进功率分配策略,并得出下列结论。

(1)采用WOA对VMD参数[K,α]寻优,以包络熵极小值作为适应度目标函数,经迭代计算得到最优参数值,相对于GA的迭代结果,WOA搜索速度更快且寻优精度更高。

(2)采用WOA-VMD分解风光波动功率信号,考虑到分解余量RES中可能包含有重要信息,再对RES进一步分解,然后结合不同类型储能装置特性,完成HESS初级功率分配,避免了EMD分解产生的严重混叠现象,并且文中所提改进功率分配策略相对于单层VMD分解的传统功率分配策略而言,其结果更为精确。

(3)将储能SOC经模糊控制优化,完成HESS功率二次修正,维持储能SOC在允许充放电范围内,有效避免过度充放电现象。