基于改进扩展卡尔曼滤波的爬架运行安全姿态估计

周豪, 韩志刚*, 胡锦仁

(1.中南林业科技大学机电工程学院, 长沙 410000; 2.湖南中模云建筑科技有限公司, 株洲 412200)

爬架(附着式脚手架)作为高层建筑施工的多节点承载平台,安全性是其运行过程中最重要的指标,一直以来是设计和使用过程中的基准[1]。目前爬架主要通过各个机位载荷和水平高差限值对架体运行的均衡程度进行安全判定和同步控制。在爬架系统整体升降过程中,由于受电机个体差异或故障、外部阻力、风载荷等因素综合影响,除了可能出现水平高差外,还可能会出现内外倾斜,利用载荷或水平高差限值可以保证架体的基本运行安全,但对架体的整个运行过程无法进行有效监管,对风载荷等侧向作用的载荷也无法进行监测,不能完全满足施工安全性和智能化的需要[2]。姿态监测是导航和制导领域常用的一种高精度安全监测方法,在相关工程领域有着广泛的利用。杜署明[3]将捷联惯性传感技术引入吊钩姿态估计系统中,在分析吊钩三维运动模型基础上,采用数据融合算法,实现姿态实时检测;陆晨等[4]基于MEMS传感器设计了一种轨道坍塌监测系统,用卡尔曼滤算法进行传感器的数据融合,用于监测采矿区轨道塌陷,保证安全生产;曹丽琴等[5]设计了杆塔倾斜姿态实时监测方法,通过卡尔曼滤波对MEMS传感器进行融合得到杆塔倾斜姿态角。卡尔曼滤波算法已成为姿态估计中的常用方法,但如果在进行融合滤波时未考虑时变噪声对MEMS传感器的影响,在复杂的环境中会出现测量精度下降的问题。

扩展卡尔曼滤波(extended Kalman filter,EKF)在对MEMS传感器进行数据解算融合时认为噪声是高斯白噪声,而实际的噪声是时变的,当系统的噪声协方差矩阵与实际不相符合时会出现滤波发散。因此,针对复杂噪声干扰下的爬架姿态估计问题,现提出一种改进的Sage-Husa扩展卡尔曼滤波算法,引入爬架实时运动速度改进滤波异常判定条件,提高滤波算法的自适应性,以期实现在时变噪声下姿态准确估计。

1 爬架运行姿态模型

1.1 姿态描述

MEMS传感器是一种应用于机器人、飞行器、杆塔倾斜、空中作业平台等姿态监测的新型传感器,具有体积小、成本低、精度高等特点[6]。爬架架体是由立杆、横杆、斜撑等组成的框架结构,在工作时受多种干扰的影响会出现倾覆、扭转、不同步等危险因素,利用MEMS传感器监测爬架工作过程中三维空间姿态角的变化,从而精准的反馈架体运行时的姿态变化,能有效提高爬架运行过程的安全性。

如图1所示,定义爬架的坐标系(b系)为载体坐标系,其中zb轴方向为爬架上升方向,yb轴指向右侧,xb轴与zboyb组成的平面垂直,地理坐标系(n系)zn轴方向指向天空,yn轴向右,xn轴与znoyn组成的平面垂直。俯仰角θ表示倾覆程度;横滚角φ表示运行出现的不同步程度;偏航角ψ表示运行时出现的架体扭转情况。

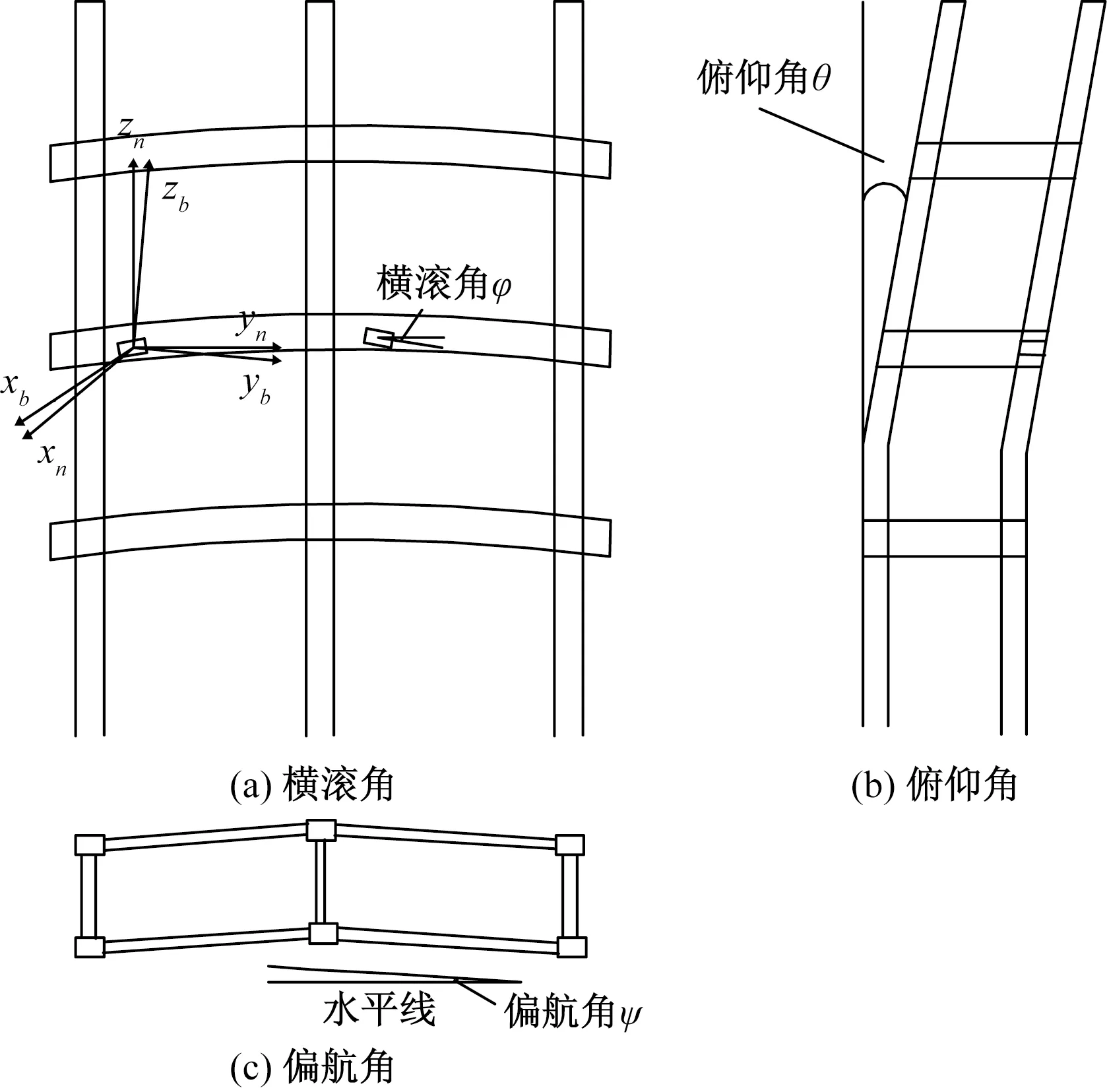
图1 坐标系与姿态角定义Fig.1 Definition of coordinate system and attitude angle

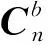
载体坐标系与地理坐标系的转换关系为

(2)

式(2)中:XbYbZb表示地理坐标系;XnYnZn表示载体坐标系。定义四元数为q,表达式为

(3)

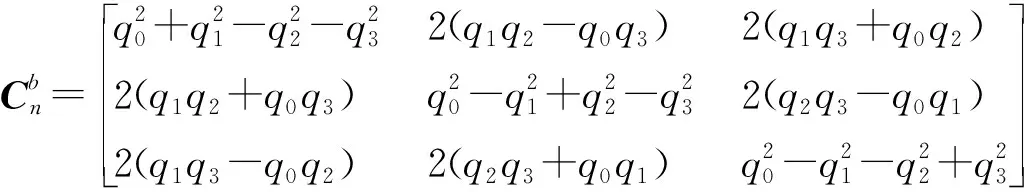
(4)

由式(1)～式(4)可得姿态角为

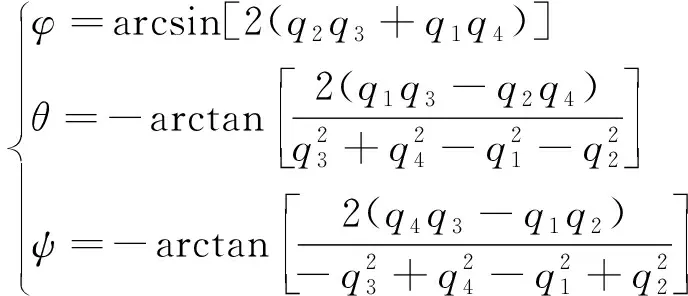
(5)

(1)

(6)

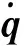
(7)

式(7)中:ωx为x轴方向角速度分量;ωy为y轴方向角速度分量;ωz为z轴方向角速度分量。

由式(6)和式(7)可得

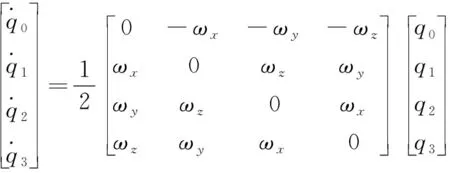
(8)

采用一阶龙格库塔法对方程进行求解可得

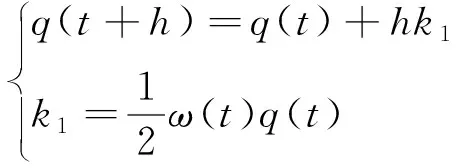
(9)

经过更新后得到的四元数为

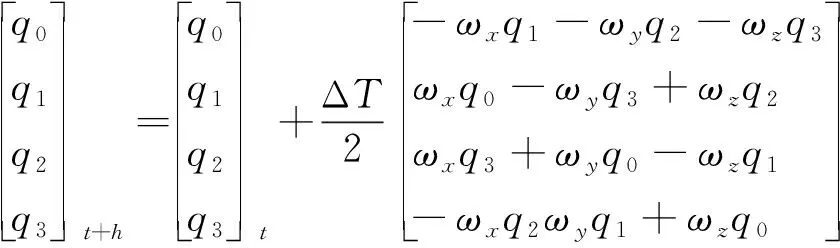
(10)

1.2 传感器误差模型

对爬架进行姿态估计时,由于爬架的安装误差时随机的,在安装MEMS传感器时对传感器进行了调零校准,因此忽略架体安装误差,只考虑传感器的误差。常用的MEMS传感器为陀螺仪、加速度计、和磁力计。陀螺仪在短时可以获得较精准的姿态信息,但由于陀螺零偏的存在,在长时间下会产生较大的误差;加速度计在静止时可获得较高的测量的精度,一旦目标载体开始运动,就会导致测量的精度下降;磁力计在测量姿态信息时容易受到磁场变化的影响,任何单一的传感器都不能获得高精度的姿态信息[9]。综合各传感器的特点,对传感器采集的信息进行数据融合,因此在进行融合前需对传感器的误差进行分析。

陀螺仪测量模型为

ω=ωm-ωb-ωn

(11)

式(11)中:ω为真实值;ωm为角速度的测量值;ωb为陀螺仪噪声;ωn为角速度测量噪声向量。

加速度计的测量模型为

a=am-ab-an

(12)

式(12)中:a为比力真值;am为加速度测量值;ab为漂移误差;an为加速度测量噪声向量。

磁力计的测量模型为

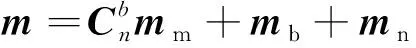
(13)

式(13)中:mb为漂移误差;mn为测量噪声;mn为磁力计测量噪声向量。

2 基于扩展卡尔曼滤波的数据融合误差补偿算法

2.1 扩展卡尔曼滤波算法

姿态解算是建立在MEMS传感器数据融合的基础上,扩展卡尔曼滤波算法(EKF)是常用的数据融合方法。由于陀螺仪存在飘移,将四元数和陀螺零偏作为EKF状态量,加速度计和磁力计作为EKF测量变量,以消除陀螺仪的误差。

建立EKF模型为

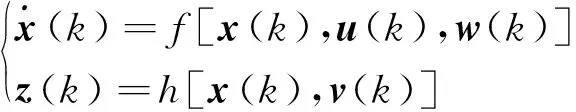
(14)

式(14)中:x(k)为系统的状态量。

x(k)=[q0q1q2q3bgxbgybgz]T

(15)

式(15)中:q=[q0q1q2q3]T为姿态信息的四元数;bg=[bgxbgybgz]T为陀螺仪角速度测量偏差。

采用姿态四元数作为测量变量z(k),即

z(k)=[q0(k)q1(k)q2(k)q3(k)]T

(16)

通过加速度计和磁力计输出的姿态四元数作为测量变量,爬架在运行时速度较慢,故加速度计的零偏不计,磁力计在测量时易受架体材料的干扰。因此,在建立测量方程时参考文献[10]给出的向量正交法,在获得姿态四元数的同时减少地磁干扰。

设旋转矩阵由三维向量i、j、k组成,分别代表机体的X、Y、Z轴向量。故有

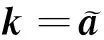
(17)

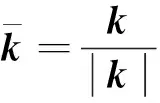
(18)

加速度计的输出用于构造机体坐标系的Z轴,将X轴强制与Z轴垂直,可以计算出i为

(19)

(20)

(21)

由此可得四元数的测量值为

z(k)=h[x(k)]=qk+1

(22)

扩展卡尔曼滤波算法步骤如图2所示。

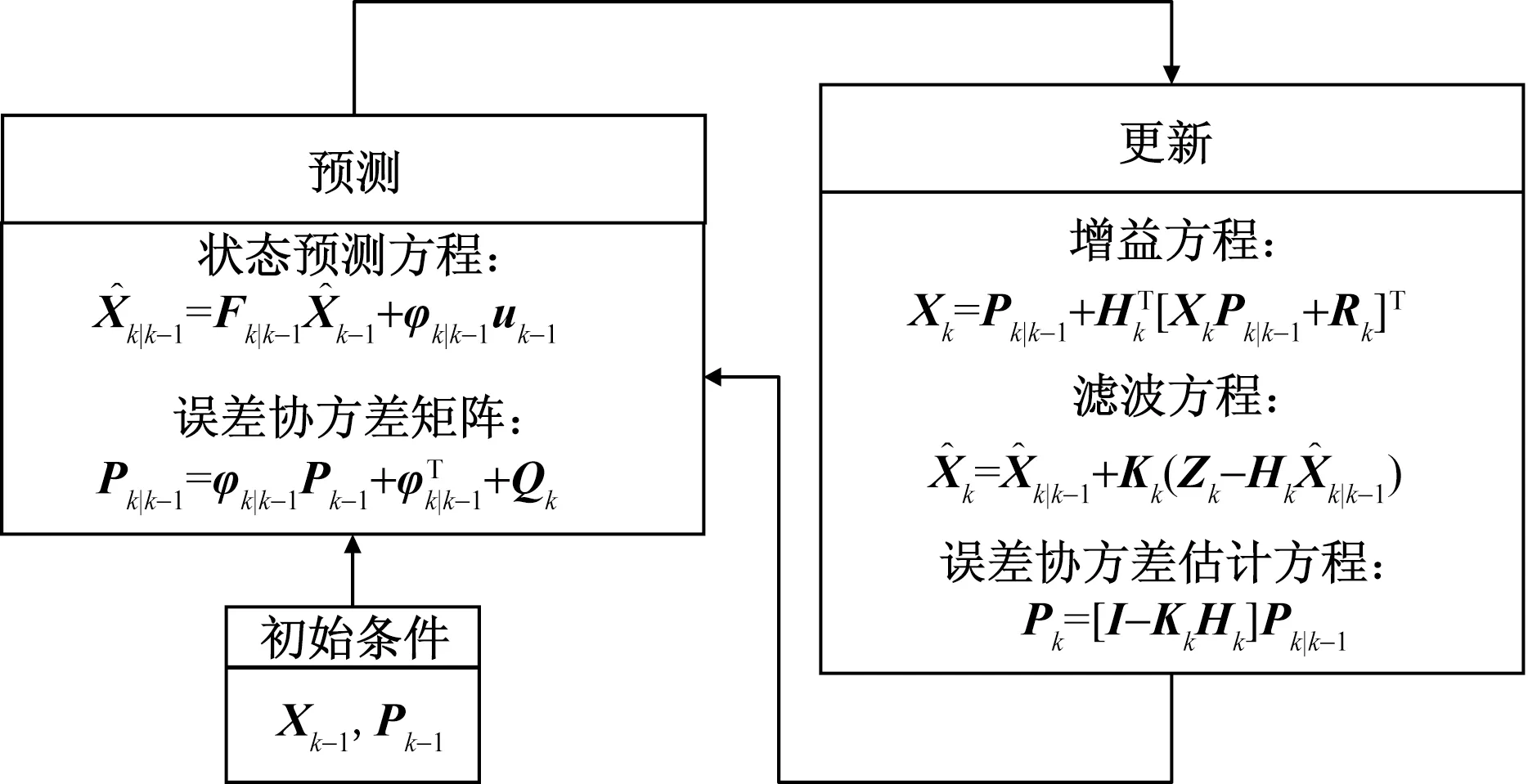
图2 扩展卡尔曼算法流程图Fig.2 Flow chart of extended Kalman algorithm

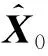
2.2 改进扩展卡尔曼滤波算法

EKF在融合MEMS传感器数据时的噪声通常被认为是均值为零的高斯白噪声。而爬架在实际应用场景中完成一次爬升的时间长,工作环境较复杂。传感器在测量时的噪声来源广泛多变,若不对噪声进行调节将会导致滤波发散,影响架体姿态的测量精度。

Sage-Husa扩展卡尔曼滤波算法(SHEKF)是EKF的衍生,可以新息自适应更新Qk和Rk调节卡尔曼增益系数,使EKF根据噪声的变化进行自适应的调节,保持高精度滤波效果[11]。其包含迭代估计和噪声更新两部分,迭代估计部分和EKF一致,噪声更新部分如下。

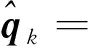
(23)

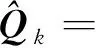
(24)

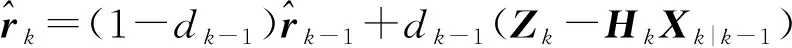
(25)

(26)

(27)

式中:b为遗忘因子,通常为0.95～0.99。

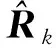
(28)

SHEKF在进行噪声统计时,对初值是否准确要求较高,当初值不准确时会导致滤波发散。因此,通过协方差匹配思想对滤波是否发散进行判定,提高滤波器的实时性和准确性。协方差匹配的思想是:判断实际新息与理论是否一致,在不一致时进行调节,爬架在爬升过程中姿态获取滤波异常的判定条件[15]如下

(29)

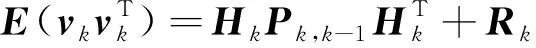
(30)

式中:γ为调节因子。

当式(29)、式(30)成立时,说明系统滤波异常,此时需对观测噪声进行调节。

爬架处于作业状态时,由于卸荷顶撑连接架体与建筑结构之间形成稳定的结构,相关的承载力也传递给建筑结构,此状态下姿态变化很小。当爬架进行爬升作业,需松开卸荷顶撑,此时整个架体相当于悬挂在空中,除了导轨限位以外,再无其他结构的支撑,架体姿态最容易发生变化且变化幅度较大。据统计爬升阶段最易出现安全事故,需要加强在爬升阶段的运动感知。

为提高爬架在不同运行状态滤波的精准性和自适应性,通过爬架的运动状态的判定实现对SHEKF的自适应调节,当爬架处于运动状态时加强滤波发散严格判定依据。因此,引入爬架运动速度对调节因子γ进行优化。

γ=100Avx+C

(31)

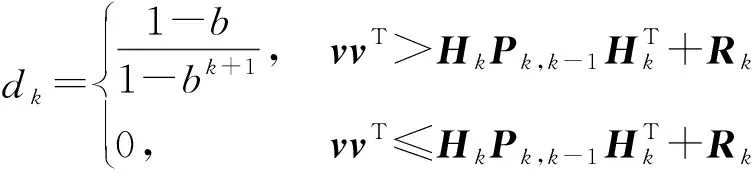
(32)

式中:vx为爬架沿导轨运动的速度;A和C为常数,可以根据实际滤波精度进行调节。

改进Sage-Husa扩展卡尔曼滤波算法如图3所示。

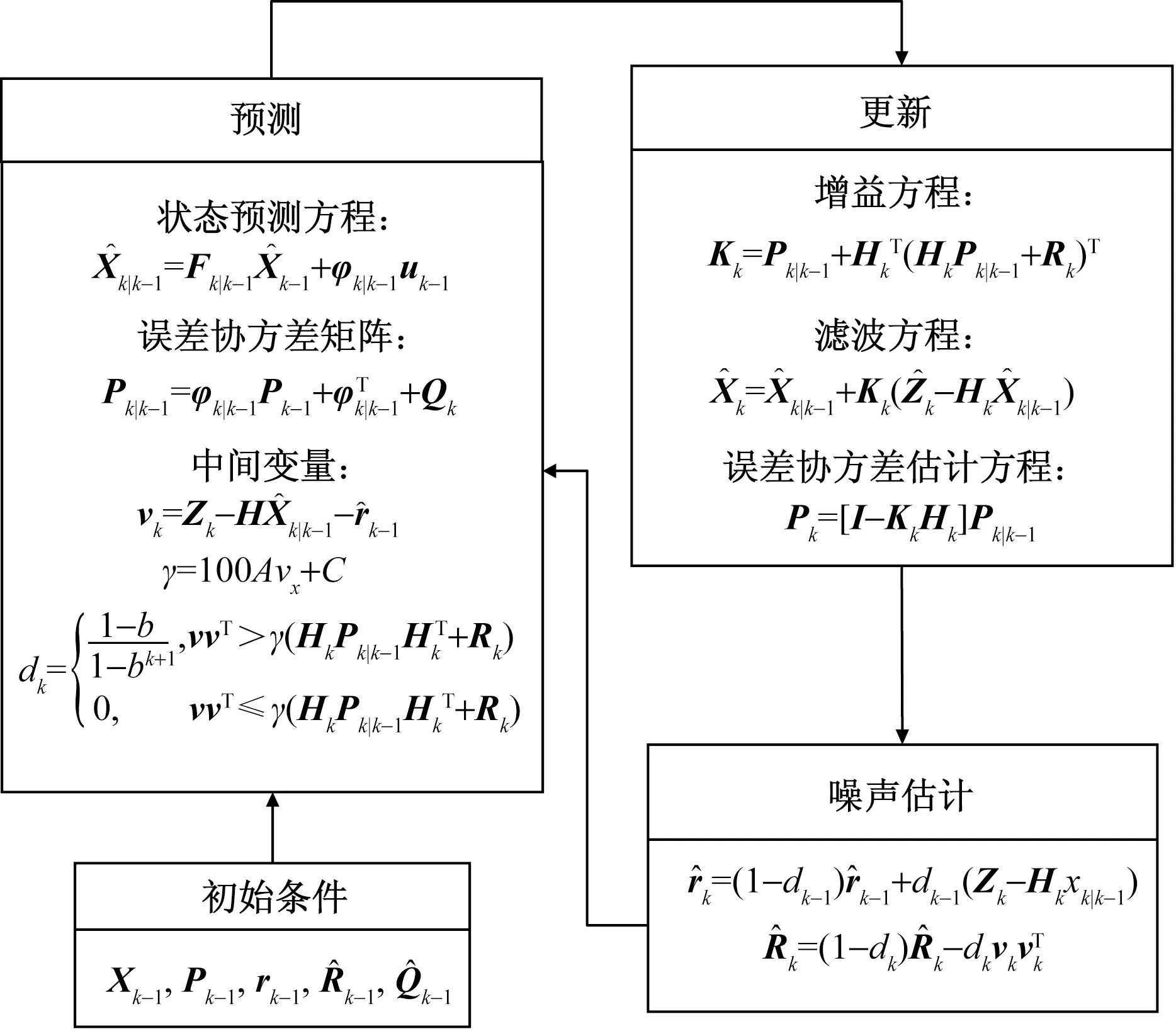
图3 改进Sage-Husa扩展卡尔曼滤波算法流程图Fig.3 Improved flow chart of Sage-Husa extended Kalman filtering algorithm

3 实验与验证

3.1 系统硬件设计

为了验证该方法的可行性,进行实验验证,爬架姿态估计实验如图4所示。实验开发环境为C/C++,开发软件为keil5和origin,实验设备主要由传感器模块、处理器模块、通讯模块、上位机组成。传感器采用Mpu9250集成了三轴加速度计、三轴磁力计、以及三轴陀螺仪,处理器采用野火指南者STM32F103CT86开发板。

图4 爬架姿态估计实验Fig.4 Experiment on attitude estimation of a climbing frame

将实验设备固定于爬架的样架上进行实验验证,考虑综合因素,从爬架一榀中任选3个机位进行试验,在传感器安装时对传感器在基面进行校零,如图4所示。

3.2 静态实验

经过试凑法确定ISHEKF的调节因子γ中取A=0.8,C=0.4,取遗忘因子b=0.98。准备3组相同的传感器,在keil5中进行相关算法代码的编译,在对应的单片机中烧录不同的算法程序。将传感器安装在架体的同一位置,置于架上静止不动。对mpu-9250初始值再次进行校准,设置mpu-9250采样频率为50 Hz,采样时间为40 s,采集到的姿态角信息如图5～图7所示。

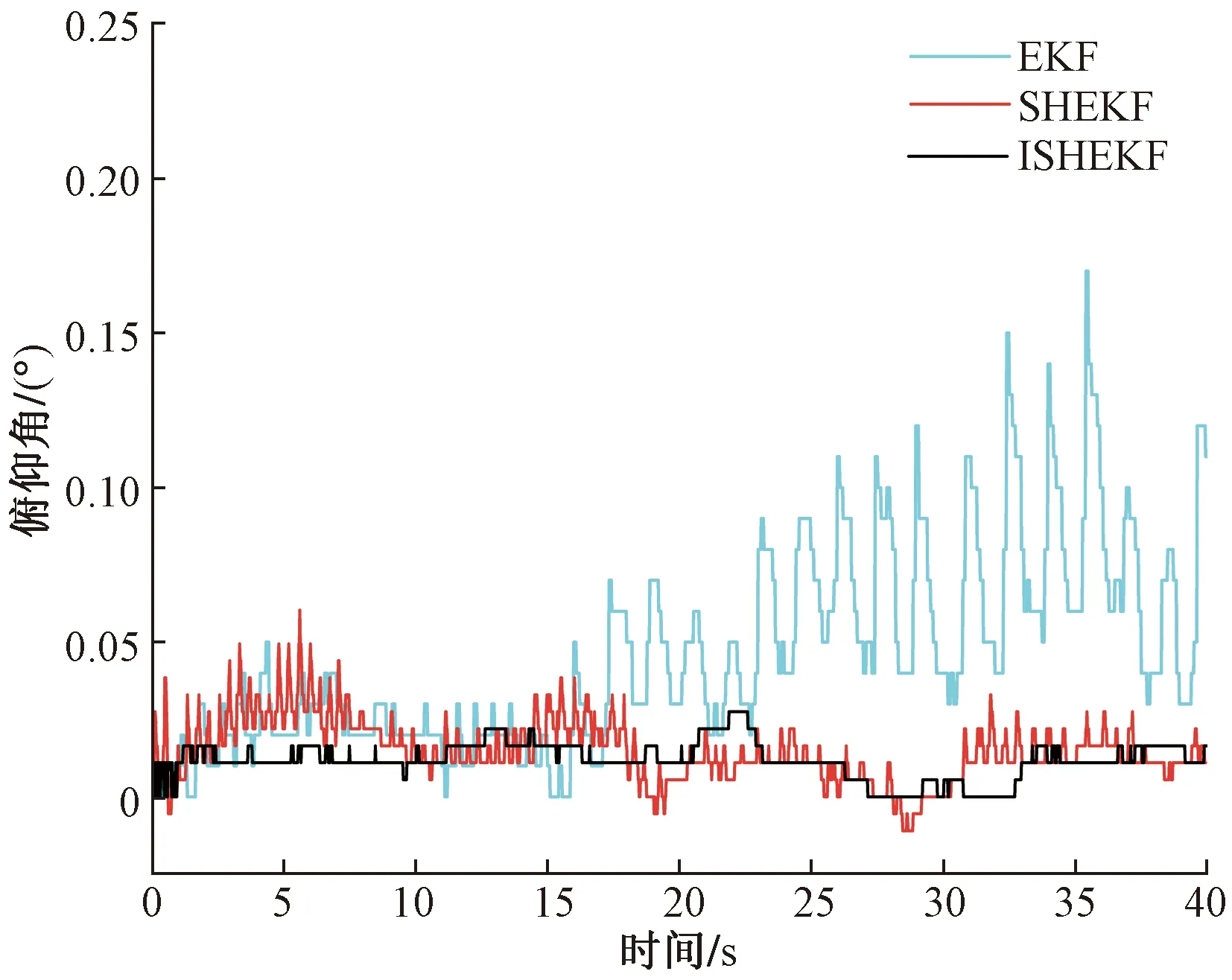
图5 俯仰角Fig.5 Pitching angle

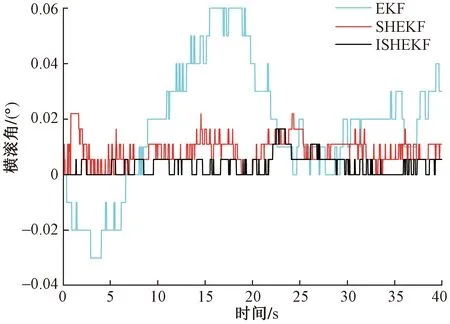
图6 横滚角Fig.6 Roll angle

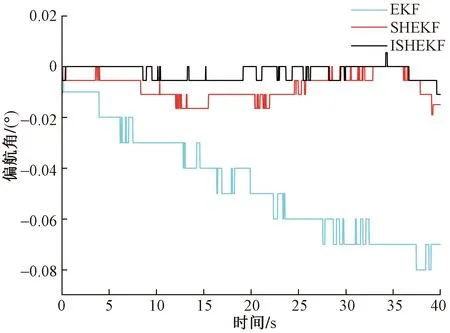
图7 偏航角Fig.7 Yaw angle

由图5～图7可知,在静止工况下,姿态角的理想的输出为0°,受环境噪声的影响,姿态角都出现了不同程度的变化。以横滚角为例,验证算法的鲁棒性,EKF的波动范围为-0.03°～0.06°,其最大误差为0.6%;SHEKF波动范围为0°～0.022 4°,其最大误差为0.224%;ISHEKF的波动范围为0°～0.017 5°,其最大误差为0.175%。ISHEKF的最大误差较SHEKF减少了21.9%,较EKF最大误差减少了70.8%。静态实验不同算法的误差性能指标评价如表1所示。

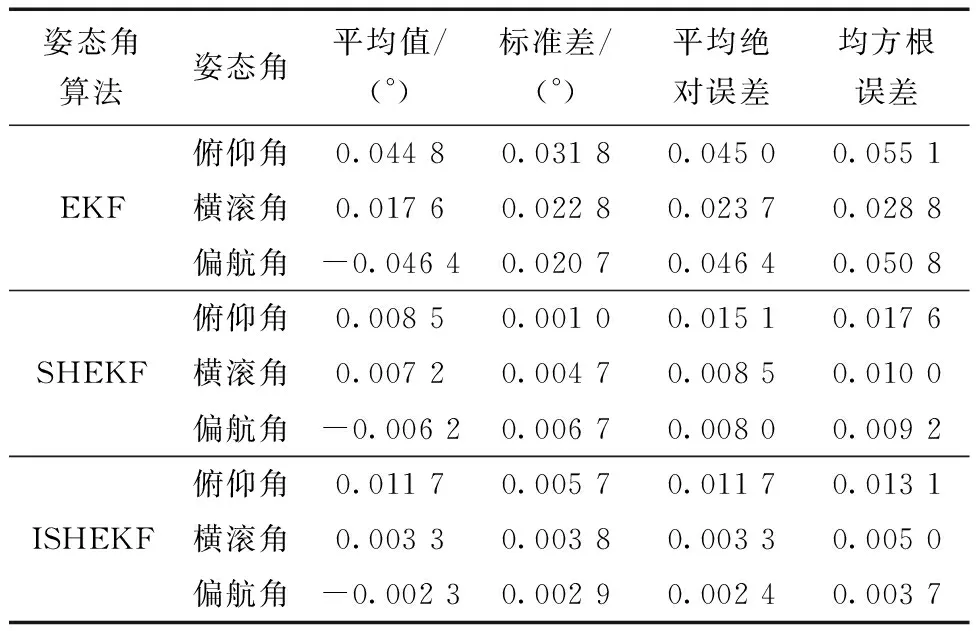
表1 静态实验不同算法误差性能比较Table 1 Comparison of error performance of different algorithms in static experiment

如表1所示的4种误差性能指标综合评价可以得出,ISHEKF在静态工况下受环境噪声的干扰最小,姿态角的输出的鲁棒性最高,更接近实际值。

3.3 动态实验

根据《建筑施工附着式脚手架安全技术规范》(JGJ 202—2010)规定相邻机位的升降不同步量应不大于30 mm[16]。整体不同步量不大于80 mm。实验样架两机位的间距为3.5 m,即理想相邻两机位横滚角的变化量为0.49°。为能更好地体现本方法的可行性,模拟运行可能出现的极端情况,在极端情况下可更直观地体现监测效果。在无外界干扰下,由于实验设备和相关条件的限制,扭转、倾覆等情形较难人为复现。不同步主要导致横滚角出现变化,短时间内俯仰角和偏航角在无外界干扰的条件下变化很小,故只采用横滚角的变化反映架体运行时的不同步姿态信息。数据采集传感器为3组,将传感器安装于架体上,对传感器进行再次校准。设置传感器采样频率为50 Hz,采样时间为15 s,根据爬架实际运行情况出现的不同步情况,设置不同测试条件。

3.3.1 模拟相邻不同步状况

假定机位1、机位3所在的葫芦出现故障不动,对机位2所在的葫芦进行提升。架体姿态变化结果如图8和图9所示。

图8 机位1和机位2之间架体横滚角变化Fig.8 Change of frame roll angle between position 1 and position 2

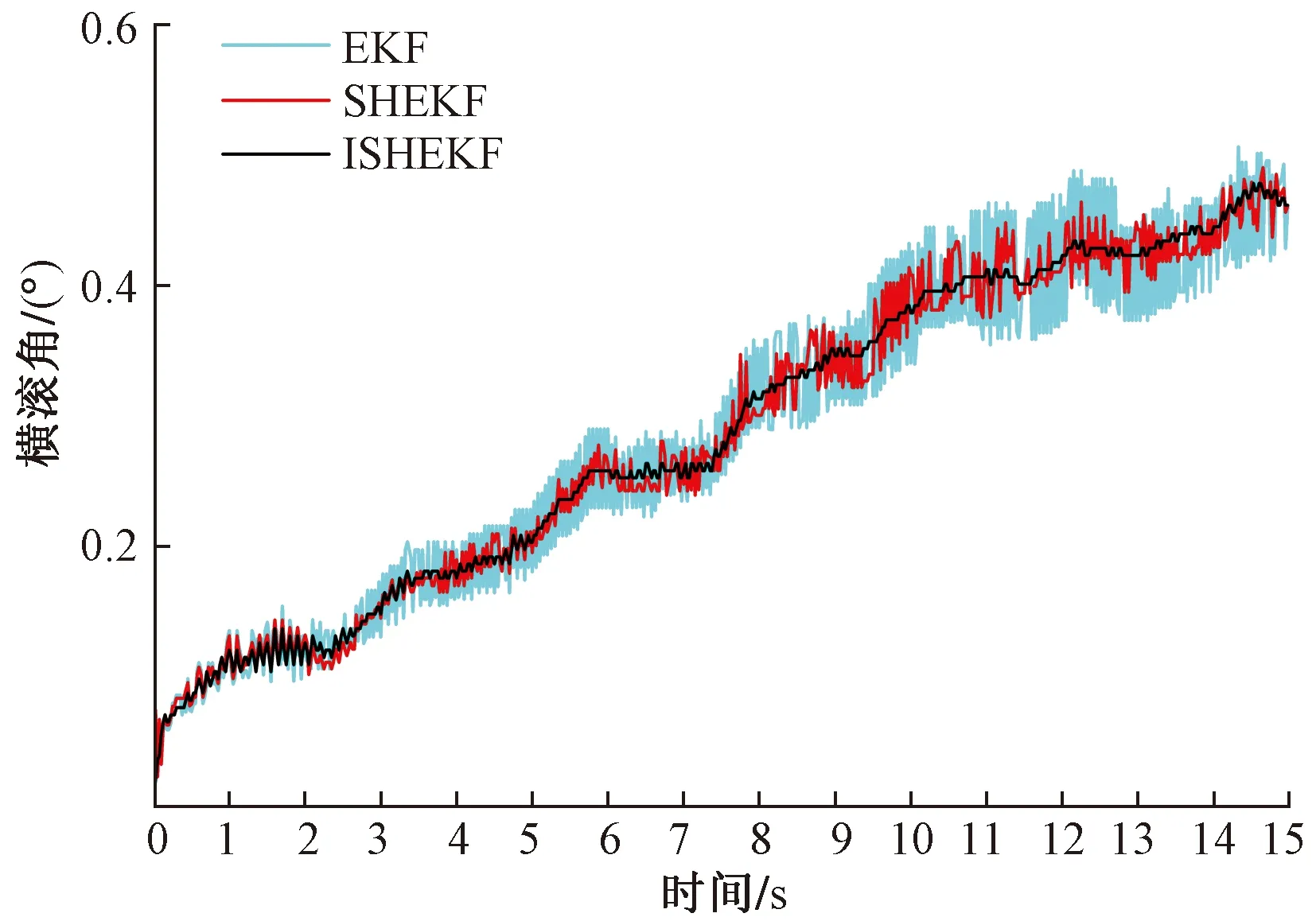
图9 机位2和机位3之间架体横滚角变化Fig.9 Change of frame roll angle between position 2 and position 3

3.3.2 模拟整体不同步状况

假定机位2所在的葫芦出现故障不动,机位1号所在的葫芦进行提升,机位3号所在的葫芦进行下降。其姿态变化结果如图10和图11所示。

图10 机位1与机位2之间架体横滚角变化Fig.10 Change of frame roll angle between position 1 and position 2

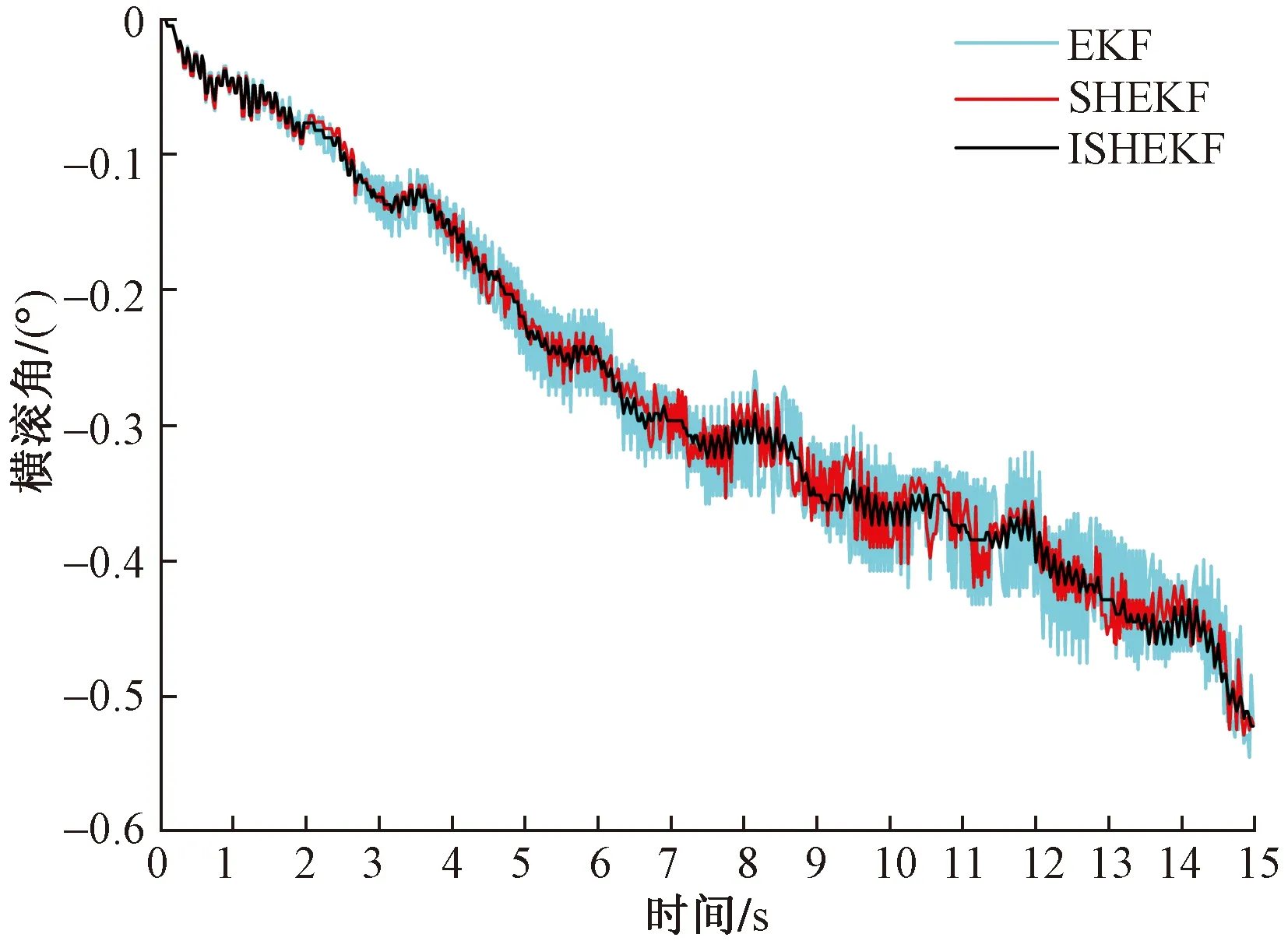
图11 机位2于机位3之间架体横滚角变化Fig.11 Change of frame roll angle between position 2 and position 3

由图8～图11可知,在动态实验时的初始2 s内,3种算法的姿态输出差别不大,随着架体继续运行,EKF受环境噪声的干扰出现了较大程度的滤波发散,SHEKF能调节噪声的变化,减少受环境噪声影响滤波发散的情况;ISHEKF能有效减少环境噪声的影响,且在架体运动时提高滤波异常判定的严格程度,较SHEKF减少了滤波发散的程度,姿态角的输出精度更号,较为真实地反映了架体姿态变化的情况。以机位2于机位3之间架体横滚角变化为例,不同算法的误差性能评价如表2所示。

表2 不同算法误差性能比较Table 2 Comparison of error performance of different algorithms

从表2可知,动态实验中ISHEKF的4种误差评价指标均优于SHEKF和EKF,说明ISHEKF具有更好的动态响应精度及鲁棒性。在经过15 s的运行后横滚角的变化范围为0.48°～0.52°,与理想值的最大误差为6.1%,证明了该方法用于爬架安全监测的可行性。

4 结论

针对爬架运行中状态感知问题,提出一种基于改进Sage-Husa扩展卡尔曼滤波算法的爬架姿态估计方法。在样架上进行了实验,对ISHEKF、SHEKF、EKF 3种算法进行了比较。在静态试验下,以横滚角为例:ISHEKF的最大误差为0.175%,SHEKF的最大误差为0.224%;EKF的最大误差为6%。说明ISHEKF有较高的鲁棒性。在动态试验下,ISHEKF能准确反映运行时的姿态角变化,传感器在ISHEKF算法下的误差性能评价指标最优。从以上结果可得出所提的ISHEKF算法能更有效地反映爬架运行姿态,减少噪声造成的误差影响,为提高爬架运行安全监测能力提供了参考价值。