岩石力学课中软岩地基极限承载力计算方法的推演与教学设计
周晓军
(西南交通大学 土木工程学院,成都 610031)
岩石力学是西南交通大学面向土木工程专业、城市地下空间工程专业和工程地质专业本科生而开设的一门必修专业基础课程。通过本课程的学习使学生能够了解和掌握岩石力学中的基本概念、基本理论和计算方法,为学生今后从事土木工程、城市地下空间工程中与岩石力学相关的工程设计和施工以及学术深造奠定坚实的基础。岩石力学课程的教学内容较多,其中软岩地基承载能力的计算是课程教学中的一个重要内容,如何使学生能够较好地理解和掌握软岩地基承载力的计算方法,是岩石力学课程教学设计和讲授方法中需要探讨和研究的问题之一。就国内目前使用的岩石力学教材[1]而言,对软岩地基极限承载力计算方法的讲解并不完整和详实,仅在教材中简要列出了岩石地基承载力的计算表达式[2-5]。在对本内容的教学过程中发现学生无法了解具体的力学模型和详尽的推演过程,因而不能明确理解和掌握软岩地基承载力的计算方法,给课程内容的教学和学生的学习均带来不便,难以实现和达到教学目标。本文结合岩石力学课程的教学实践,就软岩地基极限承载力计算方法的推演过程和相应教学内容的教学设计进行总结与分析,通过对课程讲授内容的教学设计和实践,取得了良好的教学效果。
一 岩石基地承载力计算模型的建立
为便于本科生理解和掌握软岩地基极限承载能力的计算方法,在课堂讲授此部分内容时主要从软岩地基剪切破坏的力学模型、基本假设、应力与作用力转换与分析、二维坐标系中静力平衡以及Mohr-Coulomb 强度准则的应用等开展。首先需要建立分析软岩地基承载能力的力学模型,而模型的建立需要引导学生学会应用已经讲授过的Mohr-Coulomb 强度准则。为便于学生理解和掌握,建立如图1 所示的计算和分析软岩地基承载力的力学模型。

图1 软岩地基极限承载力的力学模型
结合图1 的力学模型,需要向学生讲解软岩地基发生破坏的模式和相关的计算参数,为便于推演软岩地基的极限承载能力,主要设计的教学内容如下。
岩石地基的宽度为b,其所承受的均布荷载为ql。临近地基的附加荷载为qs。当软岩地基在均布荷载ql作用下发生剪切破坏时,地基内的岩石则会形成两个相互垂直的平直剪切面AB 和BC,而AC 平面即为岩石地基所在的地面。由此△ABC 所包围的岩石即为受剪切破坏的岩石地基,而此时的均布荷载值ql即为岩石地基的极限承载力,也是需要求解的未知量。在△ABC 中AC 边上的高h 即为岩石地基发生剪切破坏的垂直深度。
为便于分析,将△ABC 所包围的岩石块体以AC边上的高所在的边BD 划分为△ABD 和△BCD 2 个区域,并将△ABD 视为主动破坏区,而△BCD 则视为被动破坏区,△ABD 所包围的岩石的黏聚力和内摩擦角分别为c1和φ1,其容重为γ1,对应的岩石块体重量为W1,而△BCD 所包围的岩石的黏聚力和内摩擦角分别为c2和φ2,其容重为γ2,所对应的岩石块体重量为W2。
△ABC 内的岩石沿剪切面AB 和BC 走向上的厚度远大于剪切面AB 和BC 所在边的长度,因而岩石地基属于弹性力学中的平面应变问题,在分析中可取其单位厚度进行计算。同时可将△ABC 内的岩石视为均质岩石,且在平面AC 上无剪应力,在DB 面上也无剪应力。
岩石地基的剪切破坏面AB 与水平面AC 之间的夹角为α。
根据上述力学模型和采用的相关参数即可对岩石地基中主动区和被动区岩石的静力平衡状态以及岩石承载力的计算方法进行分析与推演。
二 岩石地基极限平衡状态及其应力分析
根据图1 所建立的岩石地基剪切破坏力学模型,当地基的荷载ql达到地基极限承载能力时,主动区△ABD内的岩石受压沿剪切面AB 破坏后挤压被动区△BCD内的岩石,并且使被动区△BCD 内的岩石沿剪切面BC发生剪切破坏。由此,主动区岩石会对被动区岩石施加水平挤压应力σm,而被动区岩石又会对主动区岩石施加水平顶推应力σm,两者数值相等,方向相反,均以法向应力的方式作用于BD 面上,如图1 所示。由于岩石地基AC 面和BD 面上无剪应力,因此这2 个平面为主平面,且其上的法向应力即为岩石地基的最大或最小主应力。
为便于学生理解,首先以主动区△ABD 为研究对象,对其在各个面上的应力进行分析。AD 面上承受的应力即为地基的极限承载力ql,也是需要求解的未知量。BD 面上的应力即为被动区△BCD 的顶推应力σm,剪切破坏面AB 上则有法向压应力σAB和剪切应力τAB,由此可得到主动区△ABD 各面上岩石所承受的应力及其分布状态如图2 所示。

图2 主动区岩石的应力状态
为便于在课堂讲授,并使学生理解和掌握应力的分析方法,先分析主动区△ABD 所包围的岩石静力平衡状态。为此,在图2 所示的主动区△ABD 中建立平面二维坐标系Oxy,并将剪切面AB 上的法向应力σAB和剪切应力τAB所对应的法向和切向作用力沿x 轴和y 轴方向进行力的矢量分解,即可得到主动区△ABD 内岩石的静力平衡关系式。在此,需要向学生强调的是剪切面上的应力和作用力是不同的概念。需要将剪切面上的应力换算成相应的作用力。经过转换主动区△ABD 中各个面上引起应力的作用力如图3 所示。图3 中,F1代表AD面上的作用力,F2代表BD 面上的作用力,剪切面AB 上的法向作用力为N,其在x 轴和y 轴方向上的分量分别为Nx和Ny,剪切面AB 上的剪切力为T,其在x 轴和y轴方向上的分量分别为Tx和Ty。
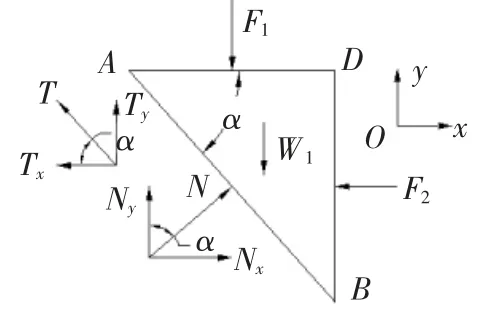
图3 主动区岩石受力
在Oxy 坐标系中法向作用力N 与其在x 轴和y 轴方向分量之间的关系式为
而切向作用力T 与其在x 轴和y 轴方向分量之间的关系式为
主动区△ABD 各面上的作用力和应力之间的换算关系为
对于式(3)而言,在讲授时需要向学生说明,式(3)中的SAD、SBD和SAB分别代表各面的面积。此处的面积实际上分别为△ABD 各边的边长与岩石地基沿其走向上单位厚度的乘积。
将主动区△ABD 各面上的应力转换为作用力后,即可在Oxy 二维平面坐标系中进行静力平衡分析,并分别沿x 轴和y 轴方向建立静力平衡关系式,即ΣFx=0 和ΣFy=0,由此得到
式(4)中W1为△ABD 包围的岩石重量,根据直角△ABD 的几何关系,可求得其重量W1为
将式(1)、式(2)、式(3)和式(5)分别代入式(4)中,并经过化简后得到以应力表示的主动区△ABD 内岩石的静力平衡方程为
由式(6)即可求得剪切破坏面AB 上的法向应力σAB和剪应力τAB的表达式为
对于主动区△ABD 内的岩石而言,其发生剪切破坏时破坏面AB 上的法向应力和剪应力应当满足Mohr-Coulomb 强度准则,即
将式(7)代入式(8)可得
从式(9)可以看出,软岩地基的极限承载力ql水平挤压应力σm、主动区△ABD 内岩石的黏聚力c1、内摩擦角φ1、岩石容重γ1、剪切面AB 与水平面之间的夹角α以及岩石剪切破裂深度h 的影响。
由于式(9)中尚未求出水平挤压应力σm,因此还需要借助被动区△BCD 来进行分析。设被动区△BCD 所包围的岩石受主动区挤压而沿剪切面BC 发生剪切破坏,则剪切破坏面BC 上的法向应力为σBC而剪切应力为τBC。主动区△ABD 内的岩石施加在被动区△BCD 岩石中BD 面上的水平挤压应力为σm,由△BCD 所包围的岩石重量为W2。为便于分析,在△BCD 区域内建立Oxy二维平面坐标系,如图4 所示。

图4 被动区岩石的极限应力状态
与前文中分析主动区△ABD 内的岩石静力平衡关系式的方法相同,将被动区△BCD 内剪切面BC 上的法向应力σBC和剪应力τBC换算成相应的作用力,并对其沿x 轴和y 轴方向上分别进行力的矢量分解,由此可得到被动区△BCD 中以应力表示的岩石静力平衡方程式为
由式(10)即可求得剪切面BC 上的法向应力σBC和剪切应力τBC,即
对于被动区△BCD 内的岩石而言,其黏聚力和内摩擦角分别为c2和φ2,当其沿剪切面BC 发生剪切破坏时,剪切面上的法向应力σBC和剪应力τBC也应当满足Mohr-Coulomb 强度准则,即
将式(11)代入式(12)可得
由此便得到了主动区和被动区之间的相互间的水平挤压应力σm。将式(13)代入式(9)即可得到岩石地基的极限承载力ql的表达式为
式(14)就是完整软岩中岩石地基极限承载力的计算表达式。根据式(14)分析,软岩地基极限承载力受被动区地面上的附加荷载、岩石黏聚力与内摩擦角、岩石容重和岩石剪切破坏深度等因素的影响。
就式(14)而言,其中涉及的参数较多,在实际计算中较为繁琐。为便于工程应用,可设主动区△ABD 和被动区△BCD 所包围的岩石黏聚力相同,即c1=c2=c;两者的内摩擦角相同,即φ1=φ2=φ;使岩石的容重也相同,即γ1=γ2=γ,由此式(14)可简化为
根据Mohr-Coulomb 强度准则,岩石发生剪切破坏时破坏面AB 与最大主平面AD 之间的夹角α 应满足
将式(16)代入式(15)可得
再利用主动区△ABD 中角α 的正切关系式可得 h=btanα,将其代入式(17)可得
为便于实际应用,可将式(18)改写为
式(19)中的3 个系数分别为λr,λc和λq将其称为岩石地基的承载力系数,3 个系数分别为
至此,经过上述的推演所得到的式(19)即为完整软岩地基极限承载力的计算公式。为便于在实际工程中应用,可在极限承载力计算值的基础上考虑一定的安全系数Fs,便可得到完整软岩中地基承载力的容许值qa,即
式(21)中的安全系数Fs一般可取为2~3。当岩石地基考虑地震和风荷载时安全系数取2,当基础承受最大活荷载时安全系数取3。
三 讨论与分析
在得到软岩地基极限承载力计算表达式以后,为使学生更深入地掌握其用法,还可结合实际对计算公式在特殊工程条件下的应用进行讨论与分析。主要讨论的内容包括2 个方面。
当被动区岩石在AC 面上无附加荷载即qs=0 时,则式(19)即可简化为
由式(22)可得,此时软岩地基的极限承载力受岩石内摩擦角、黏聚力、岩石容重和岩石地基的宽度控制。
当被动区岩石在AC 面上无附加应力即qs=0,且不考虑岩石块体的自重时,则式(19)可简化为
此时,软岩地基的极限承载力仅由岩石的黏聚力和内摩擦角提供。由式(23)可使学生进一步明确岩石黏聚力c 和内摩擦角φ 对岩石地基工程的实际意义。
通过以上对软岩地基极限承载力计算过程的推导和教学设计,使岩石地基承载力的概念和计算方法的分析思路更加清晰和明确,有利于学生理解和掌握所讲授的知识点和推演方法。将上述推演方法和教学设计通过2020—2022 年间西南交通大学开设岩石力学课程中的教学实践表明,选修该课程的本科生中经考核约90%的学生均能理解和掌握软岩地基承载力的计算方法,教学效果良好,达到和实现了课程教学大纲中对学生应掌握软石地基承载力计算方法的教学目标和要求。
四 结束语
软岩地基极限承载力的计算一直是岩石力学课程中重要的讲授内容,但现有的教材和参考文献中对推演过程和计算方法的讲解并不明确与详实,不便于学生的学习和理解。本文结合对此内容的具体教学实践,给出了软岩地基极限承载力及其容许值的推演过程和计算方法的教学设计。通过对软岩地基剪切破坏的力学模型、主动区和被动区岩石应力、剪切面应力与作用力之间的换算、岩石发生剪切破坏的极限平衡条件以及岩石Mohr-Coulomb 剪切强度的讲解和推演,使学生更容易理解和掌握相应的力学原理与计算方法,因而可实现良好的教学效果。

