海洋条件下小型堆稳压器液位智能预测研究

魏天一, 张彪, 李东阳, 谭思超, 陈佳睿, 王拓

(1.黑龙江省核动力装置性能与设备重点实验室, 黑龙江 哈尔滨 150001; 2.核安全与先进核能技术工业与信息化部重点实验室, 黑龙江 哈尔滨 150001; 3.中国原子能科学研究院, 北京 102413)

浮动核电站是小型反应堆技术与船舶工程的有机结合。液位遥测系统是船舶自动化系统的关键组成部分,事关船舶航运的安全[1]。浮动核电站对液位测量有更为严格的管控标准[2],差压法在浮动堆稳压器等储液设备的液位测量中应用广泛[3],但海洋条件将引入附加加速度干扰压差测量,液面晃荡会造成液位信号波动并引发抨击载荷[4]。因此开展液位预测研究具有工程需求和实际意义。在测量实验方面,Wei等[5]搭建运动平台并通过PLIF技术得到了运动条件下容器液面波动和压差变化情况,提供了实验研究思路;Pistani等[6]开展了矩形液舱在晃荡条件下的压力测量实验,描述了海洋条件下的压力分布特性;Cheng等[7]以核工程设备为对象,对SFR堆芯破裂过程中堆芯熔融燃料池的晃动进行了研究。但实验研究多侧重于运动条件下的压力波动和晃荡特性,并未深入讨论或提升现有测量技术。在测量优化方面,研究人员普遍关注传感器精度的提升[8]和信号处理技术改进,在考虑海洋条件引入测量偏差时多聚焦于垂荡和倾斜等运动,不能完整包络外部激励对液位测量干扰。新兴智能算法可作为辅助或优化液位测量方案的选择。谭季秋等[9]通过BP网络进行了液位信号时间序列预测,刘江莉等[10]使用卡尔曼滤波,基于液面运动公式和传感器融合得到高精度测量方案。但其研究多从信号本身或时间序列预测展开,未考虑运动激励等因素同结果的关联,在工程应用上具有一定局限性。

因此,本文对稳压器模型开展液位测量实验,基于系统参数、实验数据和人工智能,建立运动姿态等海洋条件外部激励因素与液位信号的回归预测模型,以期对实际的液位测量方案辅以参照。

1 实验研究

1.1 实验系统

海洋条件产生含垂荡、摇摆等运动的多种运动形式,垂荡通常不影响晃动特性,且实际场景中横/纵荡运动远离固有频率,对液位测量影响有限。如图1所示,实验本体为浮动堆稳压器的缩比模型,其立式储罐结构具有代表性。实验基于摇摆平台模拟海洋环境,通过变频器控制电机转速改变运动频率,曲柄机构带动摇摆台实现往复运动。实验系统可实现摇摆角度分别为7°、15°、22.5°,运动激励均为正弦信号。

图1 海洋条件下稳压器液位测量实验系统

1.2 液位测量

如图1所示,实验采用平面激光诱导荧光技术[12]捕捉摇摆条件下自由液面晃动过程,向去离子水介质中加入RhB,RhB溶液受激光照射形成激发态,并在退激过程中释放荧光,高速摄像机垂直激光面进行拍摄,经二值化处理和边缘检测[13]得到清晰气水界面和液位高度,对比并明确了液位变化和压力波动一致性。

典型压力数据如图2所示,受摇摆运动影响,压力整体上呈周期性波动,但是不同测点的压力规律差别明显且波动振幅与周期皆不同;从单一测点来看,其变化规律不易通过数学模型精准描述。

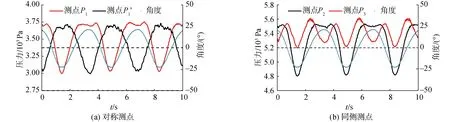
图2 压力测量结果

2 理论模型

2.1 极限学习机

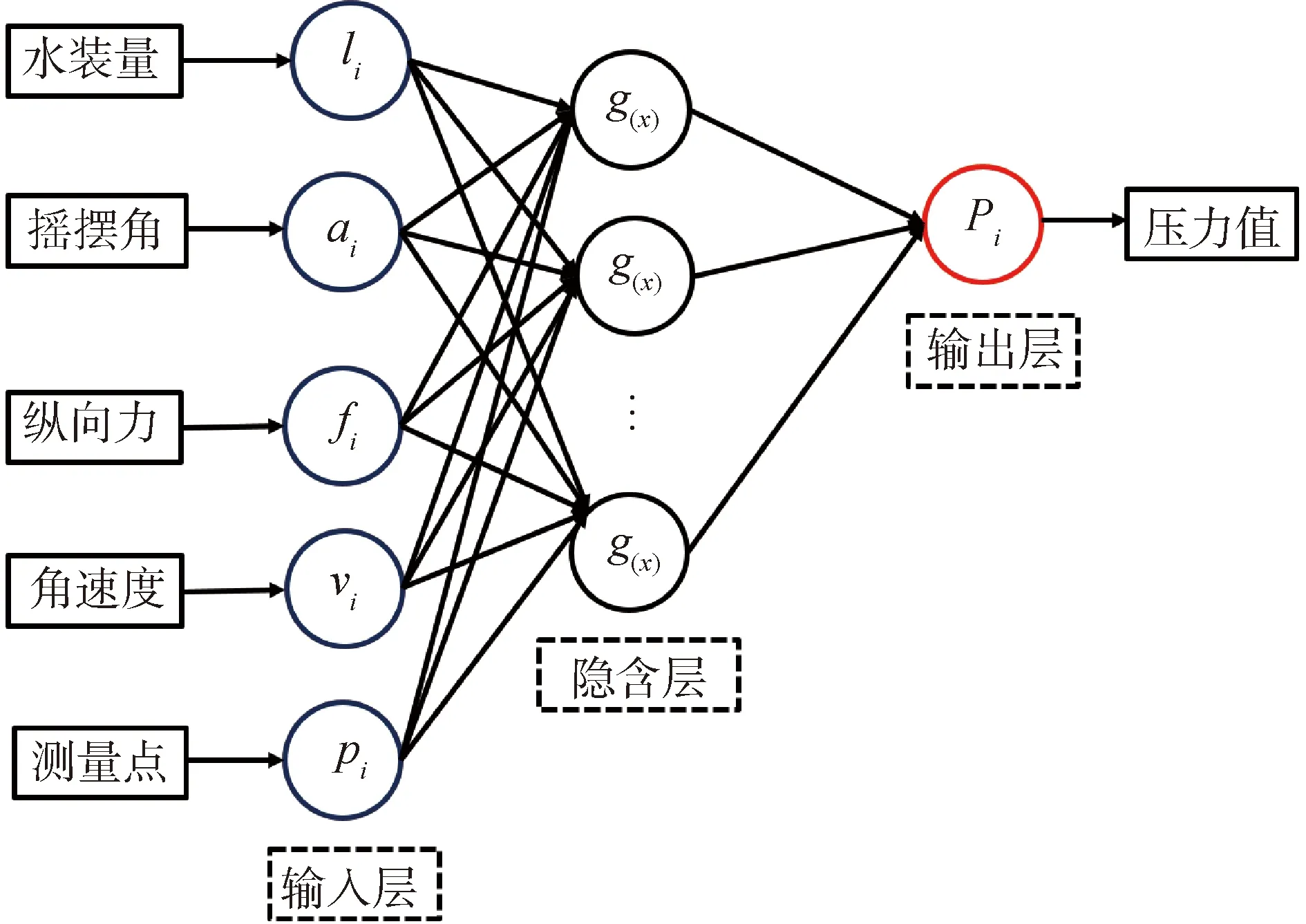
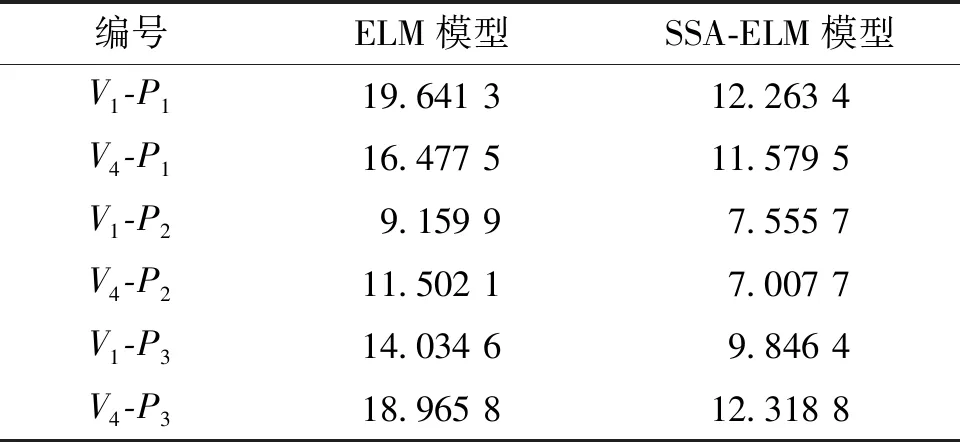
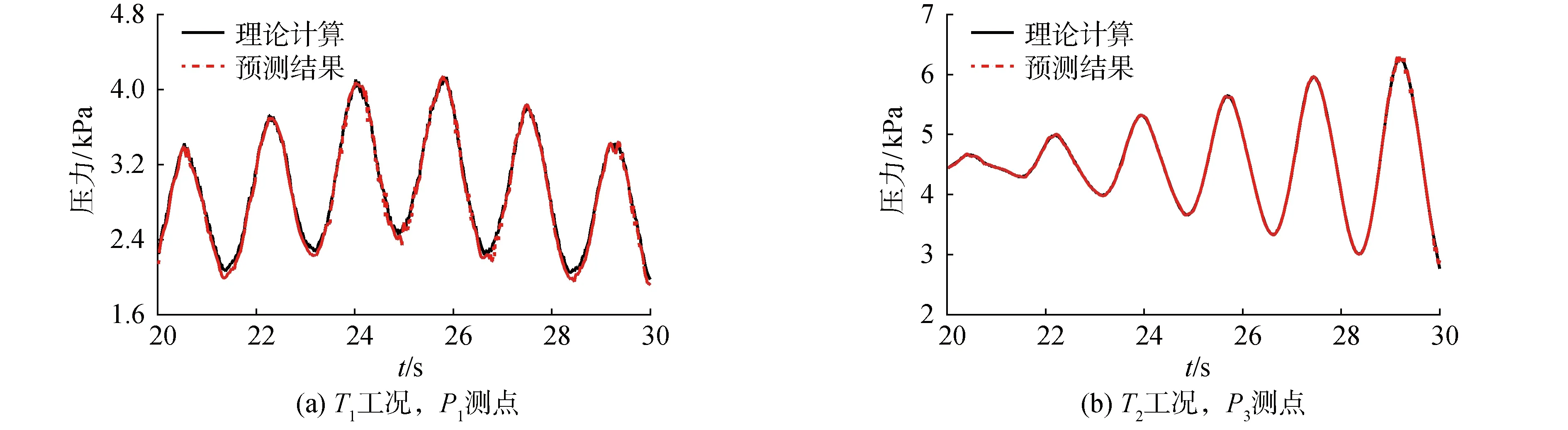
极限学习机算法[14](extreme learning algorithm,ELM)是Huang提出的一种简单高效的单隐层前馈神经网络算法。与传统神经网络不同,ELM模型将所有隐层节点的参数进行随机化处理,通过最小化由训练误差项和输出层权重范数的正则项构成的损失函数,依据Moore-Penrose广义逆矩阵理论解析求出输出权重。假定存在Q个样本(xi,ti) (i=1,2,…,Q),设输入向量和输出向量分别为xi=[xi1xi2…xin]T和ti=[ti1ti2…tim]T。可证明此时有K(K

H×β=T

(1)

设wk是输入层到第k个隐层节点的权值矩阵(weight)且k=(1,2,…,K),bk是第k个隐层节点的阈值(limen),则有:

(2)

(3)

式中:g(x)为定义激活函数,它是满足ELM通用逼近能力的非线性分段连续函数,βk是第k个隐层节点到第j个输出层节点的权值,T=[t1t2…tQ]T为输出矩阵。ELM的目标是最小化实际输出和预测值间的误差,在随机初始化连接权值及阈值后,基于最小范数的最小二乘解形式求解式(1)所述的线性系统,得到最优解:

(4)

式中H†是矩阵H的Moore-Penrose广义逆矩阵,可证明解的范数最小且唯一存在[15],计算过程不需反复修正权值和阈值。此外为了使模型具有更好的泛化性能,可以添加L2正则项,则上述求解转化为:

(5)

2.2 麻雀搜索算法

麻雀搜索算法[16]是Xue近年提出的一种新型智能优化算法,其具有参数少,寻优性能强等优点,迅速被用于优化ELM等神经网络模型[17]。在麻雀种群更新优化过程中,通常将其划分为3类角色,其中探索者寻找食物且决定种群觅食区域和方向,追随者根据探索者提供的信息觅食,预警者发现危险并决定是否撤离区域。其步骤如下:

1)初始化种群位置,确定麻雀数量n,搜索区域[ub,lb],最大迭代次数it,求解维度d及适应度函数。

2)设定示警信号为R2,种群警报阈值为ST,探索者视两者大小引领种群全局搜索或避敌转移且其根据式(6)更新位置,

(6)

(7)

(8)

3)更新麻雀种群中三者位置并计算更新后的适应度,与之前适应度值比较且标定种群最佳位置和欠佳位置,在迭代次数内重复步骤2)直至输出最优参数。

2.3 预测模型

表1 数据集设置

图3 极限学习机网络结构

极限学习机具有训练速度快和不易过拟合等优点,但随机选择权重和阈值参数的过程易造成预测模型不稳定。故本文使用全局搜索能力较强、运算用时较短的麻雀搜索算法对极限学习机改进并设计ELM-SSA模型,首先定义均方根误差(ERMS)为适应度函数:

(9)

式中Yi-f(xi)是衡量预测值与真实值之间的偏差,对数据中的异常值较为敏感。如图4所示,将初始种群位置以矩阵的形式构造为极限学习机的weight和limen,weight和limen不随极限学习机的重复训练随机更新,而是通过麻雀种群算法逐代进化,当达到验收标准后停止,此时得到最优的隐含层参数,进一步增强极限学习机的稳定性和泛化能力。

隐含层节点数目(nodes)对极限学习机的预测精度和训练速度产生重要影响。根据经验取nodes数目范围为[1∶100],选择数据集全部6 000组数据作为样本,为避免周期性数据的内在规律影响学习能力,对所有数据进行随机处理,按照[66%,33%]的比例划分为训练集和验证集,将训练集预测值和测量值的均方根误差作为评价指标,对比得到最佳隐含层节点数目,如图5(a)所示,节点数在[50,55]之间时ELM的整体性能较佳,验证结果的均方根误差控制在0.019 5附近,故本文在后续验证和测试中固定隐含层数目为50。

图5 参数选取对预测结果影响

在最佳节点基础上,经试算确定麻雀种群数量为20,最大进化次数为50,搜索者和追随者比例分别是[20%,50%],预警值ST为0.6。如图5(b)所示,对验证集乱序处理后对比预测值和实验数据偏差,直观体现了麻雀搜索对预测性能的提升,表明SSA-ELM可缩小偏差范围,提升模型精度且避免异常预测点出现。

3 结果讨论

将每组数据集前20 s的压差时序数据设定为学习样本,选择V1和V4验证集典型预测结果为例讨论。如图6所示,海洋条件下的压差信号受空间位置变化和附加惯性力作用发生显著波动,此时流体发生动势能转化,液面晃动且测量对象偏移。P1处压差信号在低载液率下对摇摆方向极敏感,呈脉冲信号特征,且随载液率增加逐步转为不规则余弦波;P2处信号整体较为规律,其波峰区域随液位的增加逐步演化为“凹谷”,体现出明显的非对称性;测点P3由于位置特殊性,其压差信号频率为运动频率的2倍,相邻周期内波型和振幅差异明显。

表2为ELM和SSA-ELM预测结果的均方误差对比,表格中的编号顺序与图6的排列顺序一致,V1-P1代指验证集V1中测点P1的预测结果且依此类推。结合图6可知,SSA-ELM模型短时得到的预测数据与测量信号高度一致,两者波峰波谷区域的局部细节吻合较好,证明预测值能够复现压差的不规则扰动,其中验证集最大均方误差均控制在19.65以内,通过SSA优化可在此基础上使验证结果的均方根误差平均下降40%左右。表明SSA-ELM模型可较好反馈运动激励、测点位置和载液率等因素对液位测量的影响,弥补数理模型表征不规则曲线的缺陷,为反应堆运维及诊断提供参考。此外在历次试算和调参中,预测输出过程(已知输出权重和输入设置后运算求解)耗时控制在0.156 s附近,即单个信号输出耗时约为0.000 312 s,完全匹配50 Hz的采集频率且具备实时预测能力。

表2 验证结果均方根误差对比

实际海洋条件较为复杂,为检验SSA-ELM对新鲜样本的适应性和广泛场景下的泛化能力,明确模型所构建输出与输入变量之间关联合理性,本文设置与训练样本差异明显的2组集合T1和T2进行测试,测试集均受到15°-3.5 s的摇摆运动激励,此外如表3所示,T1表示流量波动时稳压器载液率发生变化,T2表示受到加速度幅值变化的垂荡运动影响。

表3 测试集设置

如图7(a)所示,SSA-ELM在液位数据样本匮乏的状态下可对流量波动瞬态做出较准确的液位信号预测,其预测精度较单一ELM模型有大幅提升且将均方根误差降低至48.649 6,求解M-P广义逆矩阵耗时大约1.346 s,预测输出过程耗时约0.154 s,证明预测模型可构建起载液率和压差信号的准确关联且SSA-ELM经过小样本的训练后可适应于更广泛的工作场景。如图7(b)所示,此时测点P3的压力变化主要受到垂荡运动支配,其规律与重力方向附加加速度高度相似,即为振幅递增的正弦波动,预测值同理论计算曲线的波型一致且两者均方根误差控制在3.241 4附近。

图7 SSA-ELM测试结果分析

4 结论

1)针对浮动反应堆稳压器的液位测量问题,设计并搭建了摇摆条件下稳压器压差和可视化测量系统,得到摇摆条件下的测点压力波动规律,明确压力波动和液面位置相对变化的一致性。

2)为弥补传统数理模型在表征海洋条件等强非线性因素对液位测量的影响等方面的不足,提出应用极限学习机(ELM)构建液位压差信号同典型外部激励的回归预测模型,进行信号实时预测。

3)通过麻雀搜索方法(SSA)控制极限学习机权值和阈值更新过程,增加了预测模型精确度和稳定性,验证结果中均方根误差小于12.318 8,且单个信号平均运算耗时控制在0.000 312 s附近,表明SSA-ELM模型具备高精度同步预测功能,能够避免预期内的液位测量数据波动引起信号误触发,可为浮动核电站液位遥测和状态分析提供参考。