基于能量有限元法的耦合层合梁振动分析

陈校锋, 朱翔,3, 李天匀,3, 陈梅英

(1.华中科技大学 船舶与海洋工程学院, 湖北 武汉 430074; 2.船舶与海洋水动力湖北省重点实验室, 湖北 武汉 430074; 3.高新船舶与深海开发装备协同创新中心, 上海 200240; 4.中国舰船研究设计中心, 湖北 武汉 430064)

随着科技的进步和人们对产品舒适性要求的提高,结构在全频段内的振动和噪声越来越受到关注。传统的振动和噪声数值计算方法主要有有限元法(finite element analysis, FEA)和统计能量法(statistical energy analysis,SEA),其中有限元法在分析结构的中高频振动时,对模型的要求非常精细,这使得模型的单元和节点数目过于庞大、计算成本较高。统计能量法虽然适用于高频范围内的分析,但要求子系统有较高的模态密度,且只能得到子系统能量的均值,无法预测子系统中能量的空间变化。能量有限元法(Energy finite element analysis,EFEA)以波动理论为基础,通过建立能量密度与功率的关系,得到一个类似于热传导方程的以能量密度为基本变量的微分方程,并且可以通过类似有限元的离散对方程进行求解,适合预测结构的中高频振动响应[1-2]。

目前,已有学者将能量有限元法成功应用于各种结构中高频的声振分析。Zheng[3]和潘德阔[4]等将结构的隔声效应引入EFEA中,预测和分析了不同外部激励对高速列车结构的内部噪声响应的能量贡献,并对轮轨噪声激励进行了优化,有效降低了车内的高频段噪声。王怀志等[5]建立了航天领域中某仪器舱结构的能量有限元模型,用于振动环境的预测,其结果相比SEA模型更接近于实测值。尚保佑[6]和王迪[7]等分别利用EFEA分析损伤充液管道和损伤板的振动,通过计算损伤前后单元的能量差值准确判断了结构的损伤位置。2008年后,有学者开始将能量有限元法应用于复合材料结构。Yan[8]根据经典层合板理论,对传播波的群速度进行平均化处理,将层合板简化为各向同性板,利用EFEA较好地预测了层合板的高频振动能量密度分布。蔡忠云[9]针对含有脱层损伤的复合材料层合梁振动问题,提出了能量密度分析方法,分析了脱层处的能量传播特点和能量密度分布以及轴向冲击对损伤层合梁动态屈曲行为的影响。Vlahopoulos[10]采用谱有限元法评估材料性能和功率传递系数,以用于复合材料结构系统建模的EFEA公式,对复合材料加筋圆柱壳的模拟结果与测试数据取得了很好的一致性。Liu等[11]建立了功能梯度梁的能量密度控制方程,以此研究了功能梯度梁中金属材料和陶瓷材料占比对梁的动力学特性的影响。Xie等[12]基于薄板理论推导了正交各向异性加筋板的能量有限元方程,预测该结构的高频动力响应,并进行了相应的测试验证EFEA模型的准确性。

从目前的研究来看,对复合材料的能量有限元分析大多基于经典层合板理论,未考虑转动惯量和剪切变形效应的影响,这对于较厚板梁结构的振动响应预测会产生一定误差。本文基于一阶剪切变形理论,推导了复合材料对称层合梁的能量有限元方程,建立耦合节点处的连接矩阵来构建耦合层合梁的整体矩阵。计算层合梁的能量密度,将EFEA的计算结果与波传播法的结果进行了对比验证,分析了不同细长比下Timoshenko梁模型与Euler梁模型的能量密度分布和耦合角度对耦合层合梁能量密度分布的影响,并讨论了EFEA的适用频率范围。

1 层合梁的能量密度控制方程

1.1 能量密度和功率

复合材料耦合层合梁结构如图1所示,根据一阶剪切变形理论,对称层合梁的运动方程为[13]：

图1 复合材料耦合层合梁结构

(1)

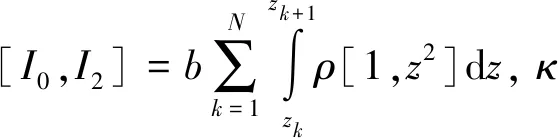
式(1)的通解可假设为:

(2)

式中:各项的系数均为复系数;klc为纵波复波数;kbc为弯曲主导弯曲波(BDFW)复波数;ksc剪切主导弯曲波(SDFW)复波数,其定义为[15]：

(3)

层合梁的时间平均远场能量密度和功率分别为:

(4)

(5)

考虑小阻尼结构η≪1时,复波数的虚部会远小于实部,因此可以忽略能量密度和功率中的二阶小量,再取其空间平均值,得到时间平均和局部空间平均的远场能量密度和功率:

(6)

(7)

1.2 能量有限元方程

比较式(6)和式(7),可以发现能量密度和功率之间存在一定的关系,以弯曲主导的弯曲波为例,该传播波的能量密度和功率有:

(8)

式中:

(9)

而对于Euler梁模型,弯曲波的能量密度与功率的关系为:

(10)

式中cgE为弯曲波的群速度,其表达式为:

(11)

(12)

利用Galerkin加权残值法对能量密度方程进行求解,可以得到:

(13)

(14)

写成矩阵形式,即能量有限元方程:

(15)

层合梁中的纵波和剪切主导弯曲波同样可以得到类似的方程,其中剪切主导的弯曲波在临界频率以下为耗散波,其能量密度在远场中可以忽略不计。

2 耦合层合梁连接矩阵

2.1 功率传递系数

实际工程中多个梁往往耦合在一起,考虑多梁耦合的模型,此时能量密度在结构耦合处不连续,需要通过功率流的连续性建立耦合节点间的联系,即连接矩阵[17],进而得到系统的整体矩阵,求解整个结构的能量密度。考虑同一平面内由N根半无限梁组成的耦合梁结构,且假设只有梁1受到外载荷激励,定义其为入射梁,如图2所示。

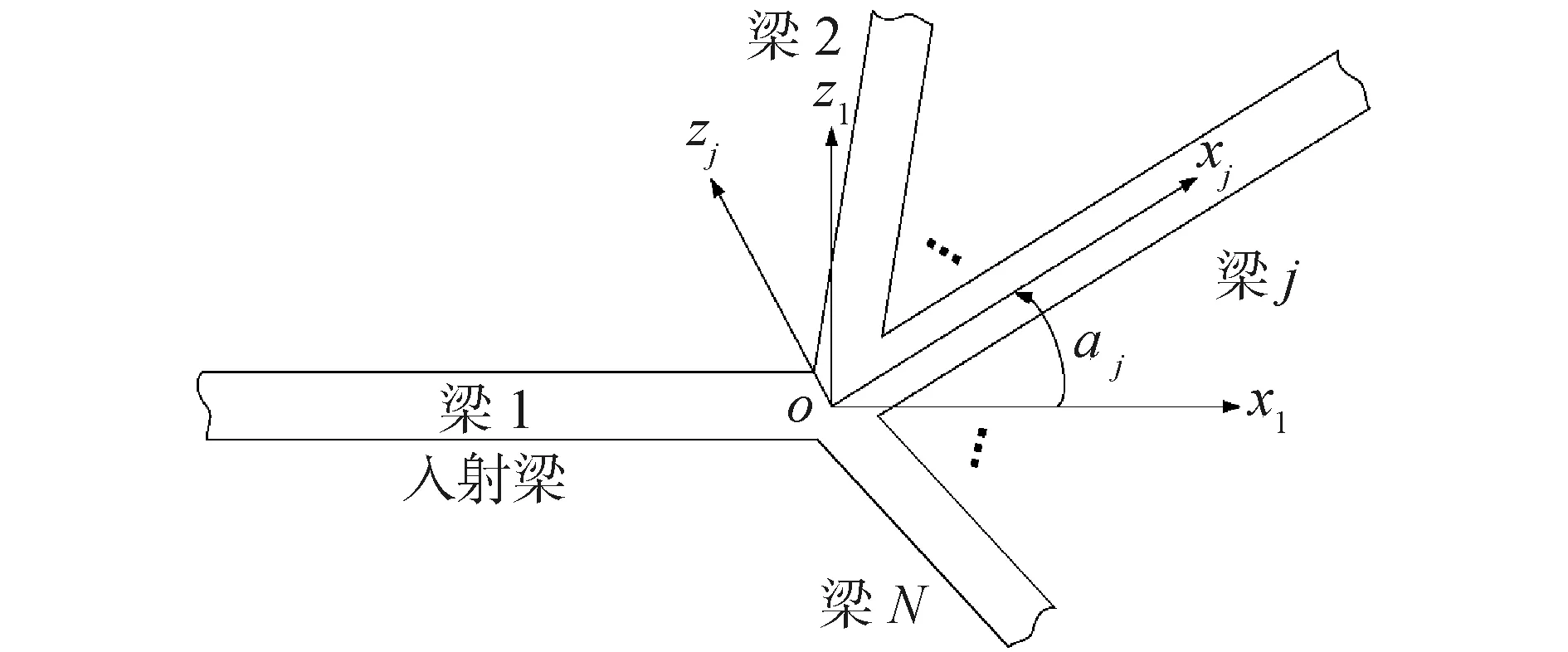
图2 半无限耦合梁结构

(16)

(17)

(18)

式中:含右上标(j)的表示梁j的参数。式(17)和式(18)中的各未知系数可根据耦合节点处的平衡条件和位移连续条件求得。分别计算式(17)和式(18)中各项与式(16)的比值,即可得到功率流反射系数和透射系数:

(19)

(20)

2.2 连接矩阵

能量密度与功率流在耦合节点处存在关系:

(21)

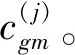
(22)

将式(21)代入式(22)并利用功率的反射和透射关系可以得到:

(23)

(24)

同样将式(21)代入式(24)并利用功率的反射和透射关系可以得到:

(25)

I=Je

(26)

式中连接矩阵:

J=PQ-1

(27)

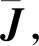
(28)

求解能量有限元方程式(28),即可得到单元的能量密度,从而进一步得出结构振动响应。

3 验证分析和讨论

3.1 算例验证

考虑图1所示的耦合梁结构,梁1与梁2的材料、铺层方式和几何特性相同,梁长l1=l2=1 m,横截面宽为b1=b2=0.01 m,高为h1=h2=0.01 m,铺层方式为[0°/60°/-60°]2 s,单层材料参数如表1所示。在层合梁1的中点x0=l1/2处施加F=1 N的横向点谐激励力,EFEA模型的单元大小为0.1 m,形函数为二次Lagrange插值函数。

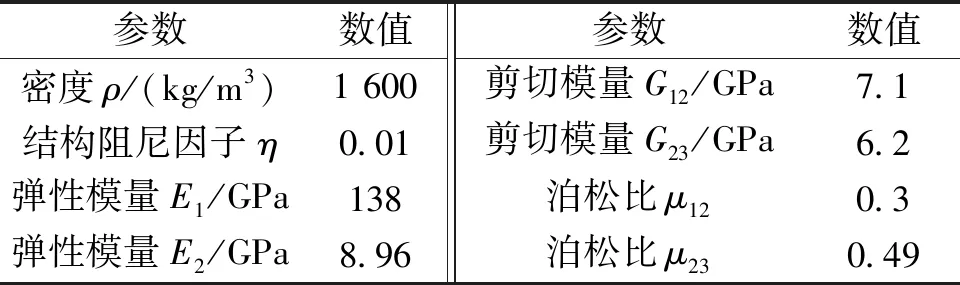
表1 耦合层合梁材料参数

将计算得到的耦合梁能量密度分布与波传播法的结果进行比较,并且均取1/3倍频程内的均值作为中心频率的能量密度:

(29)

当中心频率f=10 kHz,梁1与梁2的耦合角度α=45°时,耦合层合梁的能量密度分布如图3所示。其中能量密度的参考值为1×10-12J/m,横坐标x的区间[0,1]表示梁1的计算结果,区间[1,2]为梁2的结果,x=1为耦合节点位置。

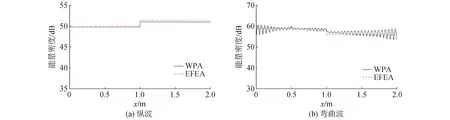
图3 耦合层合梁能量密度分布(f=10 kHz,α=45°)

从结果可以看出,2种方法得到的能量密度分布吻合得较好。EFEA计算的纵波能量密度比WPA法稍大0.5 dB左右,而EFEA的弯曲波能量密度则大致处于WPA法的均值处。在耦合节点处,能量密度出现了明显的突变,表明能量密度在结构的突变位置是不连续的。2种方法计算的弯曲波能量密度在耦合梁的两端和激励点有较大的差异,主要是因为WPA考虑了近场耗散波的影响,而EFEA则忽略了近场效应。

若根据EFEA模型单元的大小,对WPA法计算的结果取单元内均值,其结果如表2所示。结果表明EFEA得到的耦合梁能量密度与WPA法的均值结果相差1 dB以内,说明了采用EFEA预测耦合层合梁的中高频振动特性是可行且准确的。

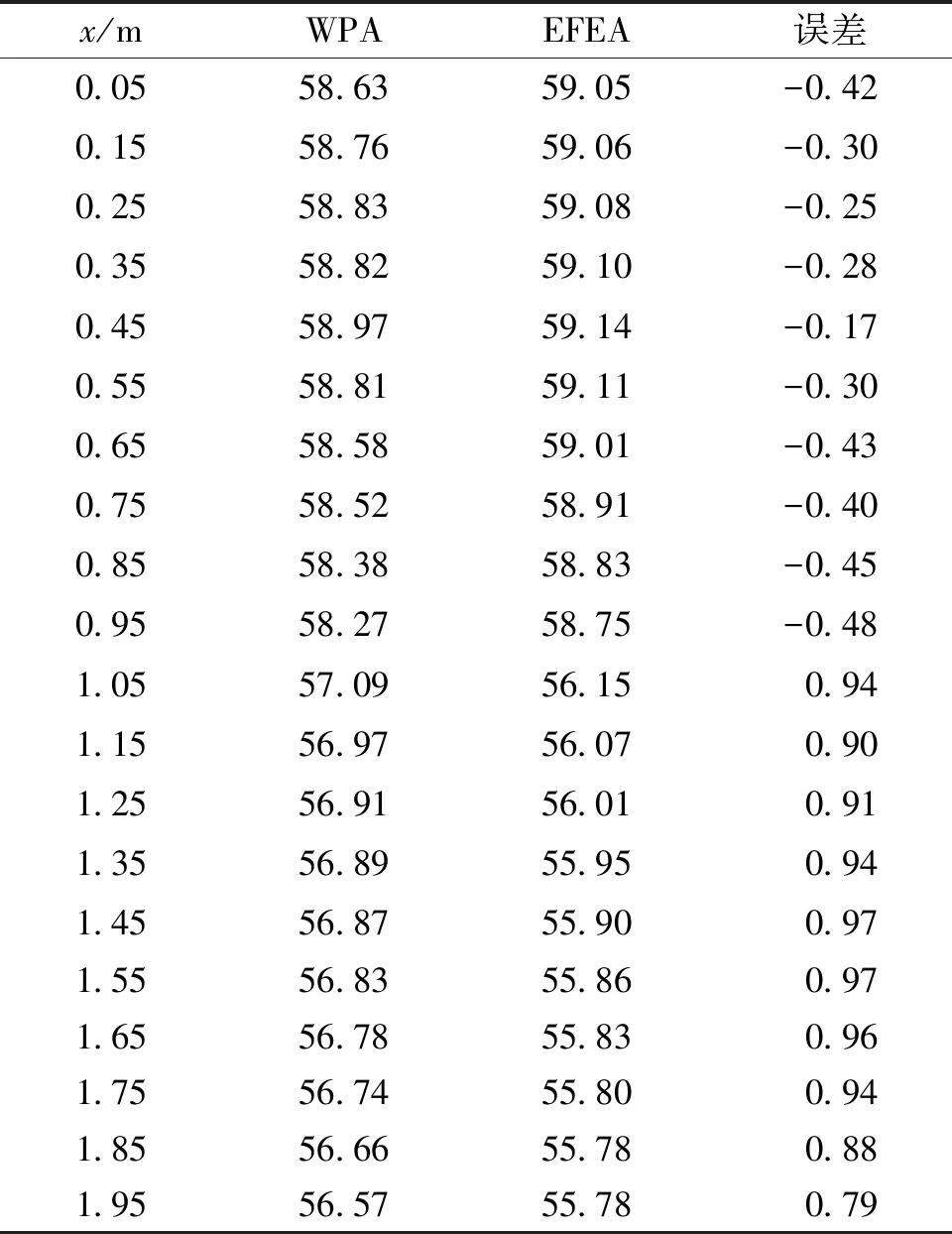
表2 耦合梁弯曲波能量密度均值

3.2 细长比

图4为层合梁的物理模型,其材料参数与表1相同,梁长l=1 m,令梁宽和高分别为b=h=0.01、0.05、0.1 m,即层合梁的细长比分别为100、20和10。比较Timoshenko梁模型和Euler梁模型的能量密度分布,以此来探讨转动惯量和剪切变形效应对层合梁振动的影响。

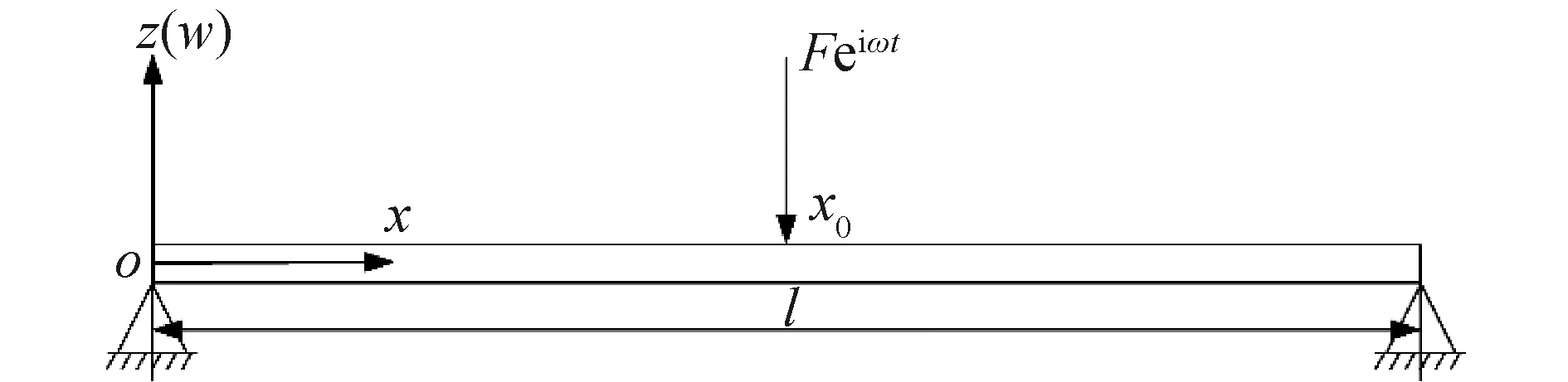
图4 复合材料层合梁物理模型

在层合梁中点处施加F=1 N的横向点谐激励力,求取不同细长比的梁在5 kHz和50 kHz激励下的能量密度分布,分别如图5和图6所示。计算结果表明,随着激励频率的增大或层合梁厚度的增加,Timoshenko梁模型和Euler梁模型能量密度分布的差异也在逐渐增大。

图5 层合梁能量密度分布(f=5 kHz)

图6 层合梁能量密度分布(f=50 kHz)

在较高频率激励下和较厚的层合梁中,Timoshenko梁模型WPA解的能量密度分布趋于平稳,逐渐逼近EFEM解,说明此时结构的能量密度分布是较为均匀的,而Euler梁模型的WPA解则始终处于随位置波动的分布特性。另一方面,层合梁的能量密度分布呈现从梁的中点即激励点向梁的两端逐渐衰减的态势,且Timoshenko梁模型的能量密度比Euler梁模型衰减得更快。该结果与文献[15]中各向同性介质梁的结果相一致,这主要是由于剪切变形效应会导致结构的能量阻尼变大,从而使得能量密度的衰减加快。因此,随着激励频率的增大和层合梁厚度的增加,转动惯量和剪切变形效应的影响会变得更加重要,对能量密度的计算结果将会产生较大的影响。

3.3 耦合角度

在耦合层合梁上作用横向点谐激励力时,激起的传播波主要为弯曲波。而弯曲波传播到耦合节点发生波的反射、透射和波形的转化则主要受耦合角度的影响。根据图1所示的耦合层合梁结构,计算不同耦合角度下耦合层合梁的能量密度分布,结果如图7所示。

图7 不同耦合角度层合梁的能量密度分布(f=10 kHz)

从图7中可以看出,梁1中纵波和梁2中弯曲波的能量密度随着耦合角度的增大而减小,梁2中的纵波能量密度则呈现相反的趋势,有了明显的增加。并且梁1和梁2中同种波形能量密度之间的差值也随着耦合角度的增大而增大。该结果说明,在耦合角度较小时,耦合节点处主要发生同种波形之间的反射和透射,不同波形之间的转换则较少;当耦合角度增大后,梁1的弯曲波传播到节点时,会有更多的成分转换为梁2中的纵波,弯曲波则相应的减小。耦合角度达到90°时,梁2的纵波能量密度(52.9 dB)甚至高于其弯曲波能量密度(50.8 dB)。

为了探讨本文层合梁能量有限元法的适用频率,本文计算了耦合层合梁在不同频率下的能量密度分布,给出了层合梁2点x=1.55 m处的能量密度,如图8所示,其中WPA法的结果为点x=1.55 m所在EFEA单元的均值。结果表明,中高频段下EFEA的计算结果较为准确,与WPA法吻合得较好。相比纵波,弯曲波能量密度在较低的频率下就有了较好的结果,其原因是层合梁的弯曲波波长较短,而纵波的波长则较长。图9给出了层合梁纵波与弯曲主导弯曲波的无因次波长(λ0=λ/l)。可以看出,在接近6 kHz时,纵波的无因次波长才小于1,即纵波波长小于层合梁的长度,弯曲波波长则在200 Hz左右便小于梁长。对照图8可以发现,弯曲波能量密度在200 Hz以上的频段就取得了较好的结果,只在个别频率下与WPA法有较大的差异。其原因可能是此时纵波的无因次波长较大,而耦合梁又存在弯曲波和纵波2种波之间的转换,使得纵波的误差影响到了弯曲波的结果。而在6 kHz以上,EFEA计算的2种波形的能量密度都更接近与WPA法的结果,具有更好的准确性。

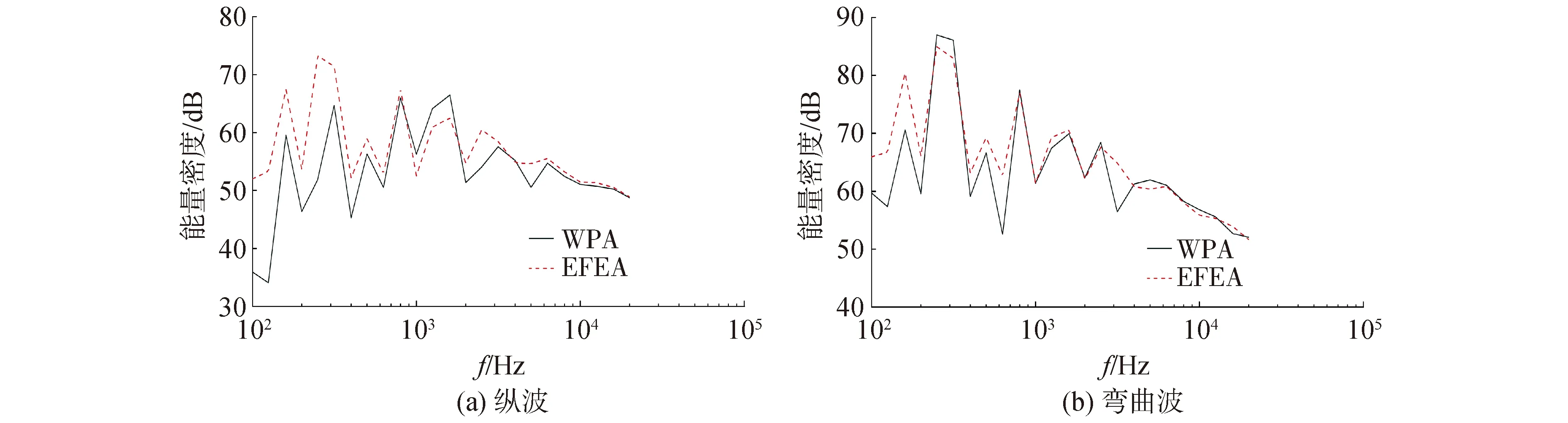
图8 层合梁2点x=1.55 m处的能量密度(α=45°)

图9 纵波与弯曲主导弯曲波的无因次波长

能量有限元法求取的能量密度是均值,当传播波的波长大于梁的长度时,即无因次波长大于1时,均值就无法很好地表示层合梁各点的响应结果,会产生较大的误差。因此,至少在传播波的波长大于梁长所对应的频率以上,EFEA才能较好地预测耦合层合梁的中高频振动。

4 结论

1)采用EFEA预测耦合层合梁结构的中高频振动响应是准确的,并且在传播波的波长小于梁长的频率下能取得更好的结果;

2)不同细长比下Timoshenko梁模型与Euler梁模型的能量密度分布的结果表明,在高频激励下和短粗梁中,转动惯量和剪切变形效会对结果产生显著的影响。

3)层合梁中的振动波传播到耦合节点处发生的反射、透射和不同波形之间的转换会受到耦合角度的影响。