气体超声换能器动态性能测试方法研究

章圣意,姚海滨,林 恒,卜勤超,赵伟国

(1.浙江苍南仪表集团股份有限公司,浙江 苍南 325800;2.上海裕达实业有限公司,上海 200240;3.中国计量大学计量测试工程学院,浙江 杭州 310018)

0 引言

超声流量计是通过超声波信号在流体中的信号变化来计算流速的流量仪表,具有低压损、高精度和宽量程比的特点[1-2]。超声时差法是目前超声流量计中应用较为广泛的方法[2]。然而,超声波换能器的性能很大程度上决定了超声流量计的测量精度以及稳定性。因此,准确测量超声换能器的性能对超声流量计的性能提升具有重要的意义。

超声换能器的性能研究可分为稳态性能和动态性能。超声换能器稳态性能主要为阻抗特性,包括机电耦合系数、机械品质因数和频率特性等。动态性能主要是超声换能器在工作状态下的性能指标,包括灵敏度和波形特征[3]。在稳态性能方面,李家宽等基于虚拟仪器技术设计了新型压电器件阻抗测试分析系统[4]。陆飞、郭建中等研究了基于计算机控制以及虚拟仪器设计在相位检测原理下实现的超声换能器阻抗分析仪的设计[5]。在动态性能方面,陈思从换能器灵敏度和频率特性等方面分析换能器一致性[6]。其侧重于对换能器进行仿真分析。

综上分析可知,超声流量计的性能指标与测量中回波信号的特征密切相关。对此,本文提出了1种超声换能器动态性能测试方法,设计了自动测试系统。该方法采用高斯模型对回波信号进行建模,以获得回波信号的特征参数,实现对超声换能器的动态性能评价。

1 测量原理

超声波回波信号的响应特性不仅与超声换能器的设计结构(包括背衬、压电晶体、匹配层等)有关,还与脉冲激励信号的波形、频率以及激励个数有关[7]。

超声换能器回波波形如图1所示。

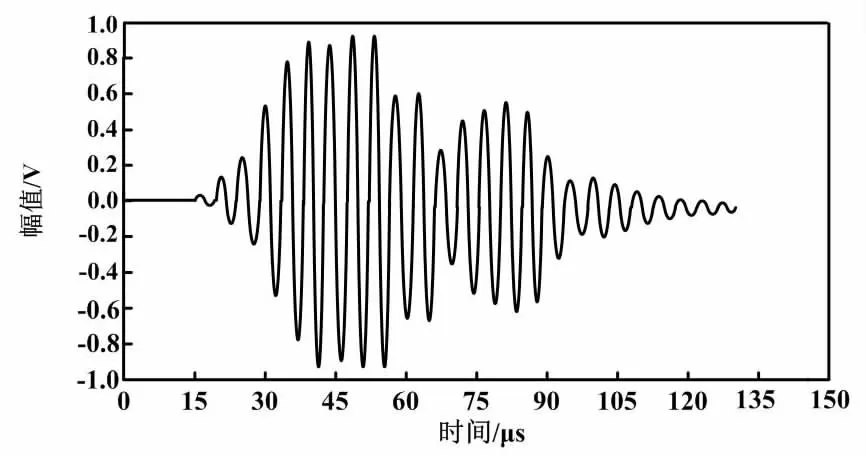
图1 超声换能器回波波形

通过回波信号建立的数学模型为:

s(θ,t)=g(θ)u(t)

(1)

式中:s(θ,t)为回波信号,V;θ为特征参数向量,包括回波信号幅值β、带宽因子α和回波信号中心频率fc参数;t为时间,s;g(θ)为传递函数模型;u(t)为激励信号,V。

其中:α既反映了回波信号的带宽范围,又反映了回波信号在时域中的持续时间;fc与换能器本身的中心频率以及传输路径的频率特性有关。

回波特征参数最优解需要以实际回波信号采样数据与基于高斯模型的回波信号之间的差异大小作为判断依据。本文引入基于最小二乘法的目标函数式,以求取基于高斯模型的回波信号的最优解。

本文以人工鱼群算法搜索回波信号的特征参数,通过目标函数的最小值求取回波信号的最优解。目标函数是采样回波数据与回波信号模型的平方差[7]。

(2)

式中:x(n)为采集超声换能器的回波数据,V;N为离散回波采样点数量;θ(k)为第k次迭代时的回波参数向量估计值;s(θ(k),n)为第k次迭代时的高斯模型,V;f(θ(k))为第k次迭代时的目标函数值,V2。

本文计算θ的欧式距离,并以其作为超声换能器动态性能的一致性准则。欧式距离计算式为:

(3)

式中:θ1、θ2分别为超声换能器1、超声换能器2经归一化处理后的特征参数向量;d(θ1,θ2)为超声换能器1、超声换能器2的欧式距离;θ1i、θ2i为参数向量中的第i个参数向量。

本文由式(3)计算被测超声换能器之间的欧式距离,并将其作为比较超声换能器之间动态性能一致性评估的依据。欧式距离越小,则超声换能器的动态性能一致性越好。

2 回波信号建模

针对回波信号模型的相关研究,常用的数学模型分别为高斯模型[8]和混合指数模型[9]。本文对两种回波模型进行研究,从而得到最优模型。

高斯模型的换能器回波信号为1个由信号幅值、带宽因子、到达时间、中心频率以及相位这4个参数决定其性能的非线性函数[8]。因此,换能器回波信号可由s(θg,t)表示。

s(θg,t)=βe-α(t-τ)2cos[2πfc(t-τ)+φ]

(4)

式中:θg为高斯模型的参数向量,θg=[βατfcφ];τ为回波信号到达时间,s;φ为回波信号初相位,rad,其值一般取0。

高斯模型的参数向量为θg=[1.08 V 0.003 8(kHz)28.9×10-5s 208 kHz 0]。

基于高斯模型的回波信号如图2所示。

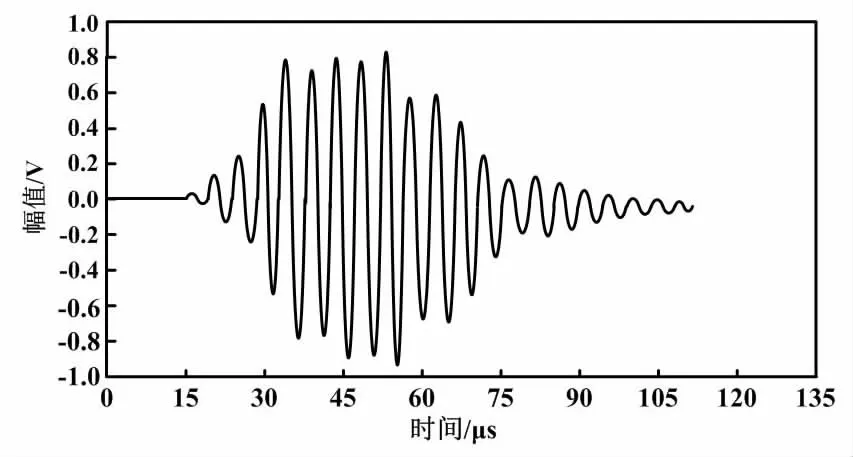
图2 基于高斯模型的回波信号

由图2可知,基于高斯模型的回波信号振荡小波较多且回波峰值上升沿与下降沿的变化速率相近。对比基于高斯模型的回波信号与实际对射回波信号可知,基于高斯模型的回波信号的上升沿部分回波台阶变化与实际波形较为接近,但下降沿部分变化速率过快。

相比于高斯模型混合指数模型的上升沿与下降沿为非对称变化,高斯模型上升沿部分变化速率较快而下降沿部分变化速率较慢。

混合指数模型表达式为[9]：

(5)

式中:θh为混合指数模型的回波特征参数向量,θh=[βTmτfcφ];m为整数,决定了回波信号能量的集中程度,取值范围一般为[1,3];T为回波信号的存在时间,s。

回波特征参数向量为θh=[1.0 V 1.3×10-5s 2.0 3.8×10-5s 200 kHz 0]。

基于混合指数模型的回波信号如图3所示。

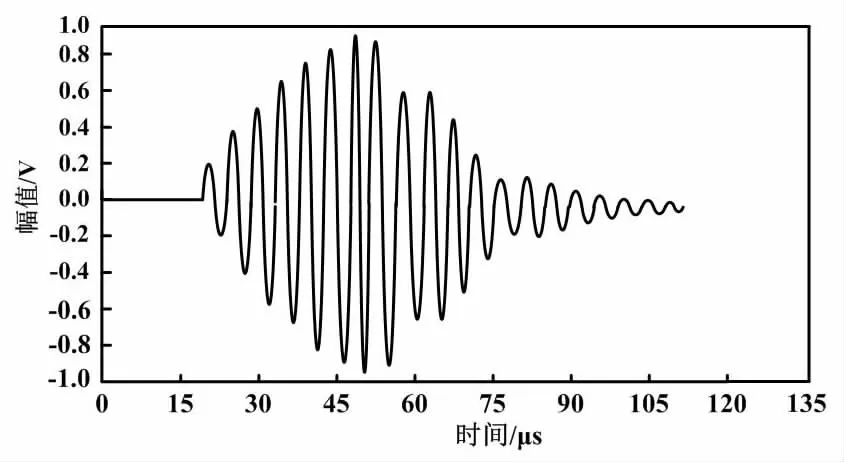
图3 基于混合指数模型的回波信号

由图3可知,基于混合指数模型的回波信号在时域上为非对称信号,回波信号到达时快速振荡在下降沿部分缓慢衰减。基于混合指数模型的回波信号近似于实际回波信号,但还有一定的差别。这主要是回波信号到达时回波各峰值的幅值变化速度较快,而回波下降沿部分变化则过于缓慢。

从以上对2种模型的仿真回波信号与实际回波信号的分析比较可知,2种模型都不能完全反映实际的回波信号。虽然在上升沿部分都近似于实际的回波信号,但其下降沿都有所差异。结合阈值法测量回波信号到达时间原理,回波上升沿部分的峰值特征用于确定其到达时间,而回波下降沿的波形变化并不影响测量。因此,本文考虑2种模型的仿真回波信号与实际回波信号的上升沿部分的相似度。

为了直观地量化分析2种模型与实际回波信号的相似程度,以得到回波信号特征参数的最优模型,本文应用最小二乘法构建目标函数。其表达式为:

(6)

式中:f(θ)为目标函数,V2;x(i)为采集得到的实际回波信号,V;s(θ)为2种模型最优估计后的仿真回波信号,V。

本文随机选取超声换能器1,采集其对射回波波形,基于高斯模型和混合指数模型分别建立其最优仿真回波信号,并计算2种仿真模型和实际回波信号的差异。通过计算可知,基于高斯模型的回波信号的目标函数值是0.27 V2,远小于基于混合指数模型的目标函数值0.58 V2。由此可知,高斯模型建立的仿真回波信号更近似于实际的超声波换能器对射回波信号。因此,本文采用高斯模型建立回波信号的模型。

3 回波特征参数的估计

基于高斯模型的回波信号特征参数向量为θ=[βατfc]。其中,回波信号到达时间τ主要受声速和环境变化的影响,因此不作为一致性分析的主要特征参数。回波放大电路中的增益值G可代替回波峰值。因此,本文以超声波回波特征参数向量θ′=[αGfc]作为气体超声换能器一致性评价的依据。3个特征参数都决定回波信号的特征。α作为带宽因子,决定回波信号在时域中的持续时间。α越大,则持续时间越短;反之,则持续时间越长。同时,α也体现了回波信号幅值变化的速度。G作为回波信号增益值,反映了超声波换能器的对射灵敏度。G越大,则对射灵敏度越小。

基于非线性模型的参数估计方法主要有高斯-牛顿算法和模拟退火算法。高斯-牛顿算法极大地依赖于初始值的设定,极易陷入局部最优解。模拟退火算法收敛速度慢、计算耗时长。人工鱼群算法是在动物群体智能行为研究基础上提出的1种新型优化方法,采用自下而上的设计方法。人工鱼群算法具有较好的全局寻优能力,能避免陷入局部最优解;对初始参数设定的敏感性较低,允许范围较大[10]。因此,本文将人工鱼群算法应用于超声换能器回波信号特征参数的最优估计。

人工鱼群算法流程如图4所示。

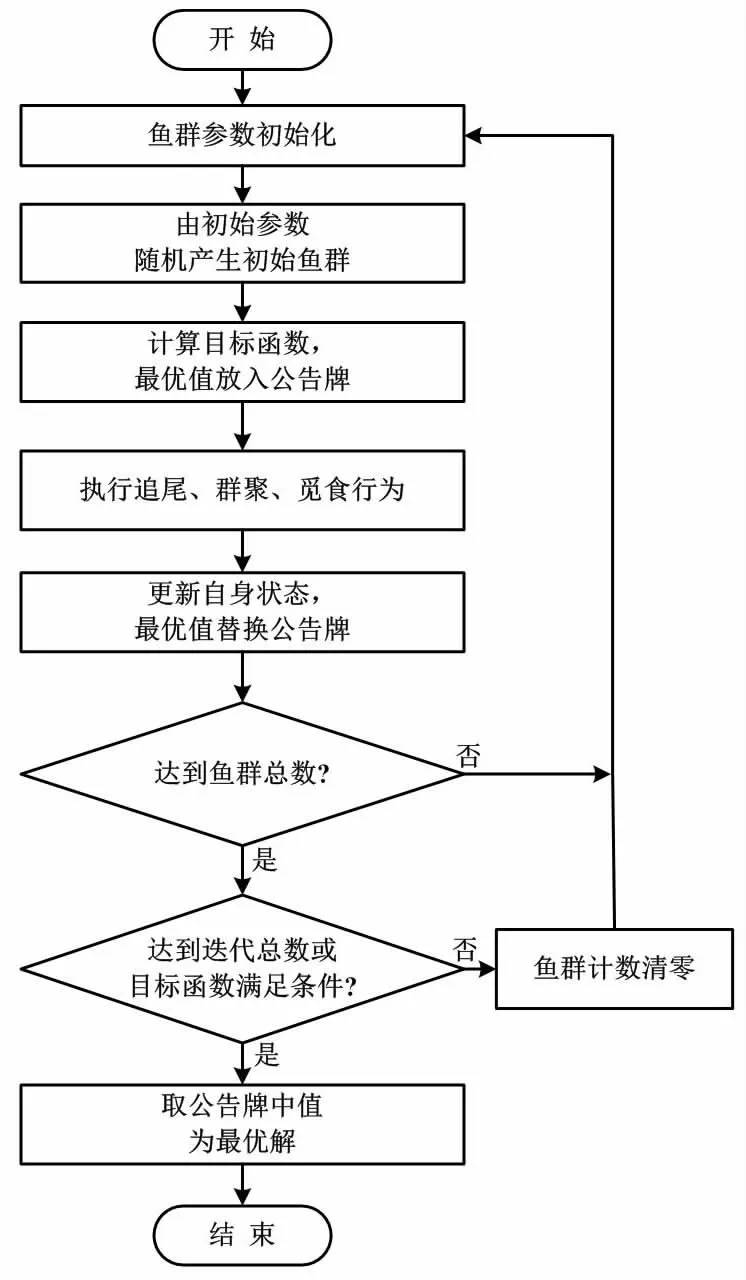
图4 人工鱼群算法流程图

4 方法实施

4.1 硬件设计

超声换能器动态性能测试系统硬件如图5所示。

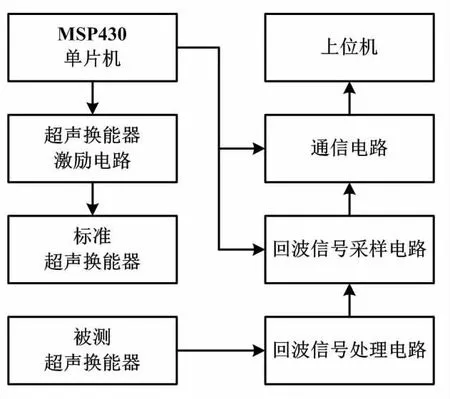
图5 超声换能器动态性能测试系统硬件框图

超声换能器动态性能测试系统采用MSP430单片机控制,主要包括激励电路、回波信号处理电路、回波信号采样电路和通信电路。由于超声波信号在气体中的衰减较大,需要较高的电压激励超声换能器。直流升压电路将电压升至20 V,激励的脉冲信号由TDC-GP22芯片产生。脉冲信号的频率和个数可根据需要更改。脉冲信号通过控制场效应管以驱动变压器。由于回波信号仍难以满足测量要求,其接收后还需要先经过差分放大、滤波和二级放大处理,再经过高速采样电路,最后将回波数据发送给上位机。

根据香农采样定理,采样频率必须高于信号频率2倍以上,并且采样频率越高则信号失真度越小。由于超声波回波信号的频率为200 kHz左右,采样电路的采样频率为5 MHz。高速模拟/数字(analog-to-digital,A/D)采样电路由复杂可编程逻辑器件(complex programmable logic device,CPLD)控制。当接收到单片机发出的采样信号后,CPLD控制A/D采样芯片采集回波信号,并将数据存储于存储芯片之中。采样结束后,CPLD将数据传送至单片机。单片机通过串行通信电路将数据传输至上位机。A/D采样芯片选用AD9237芯片。该芯片的采样频率可达20 MHz。CPLD芯片选用EMP240T100C5芯片。晶振频率选用50 MHz。

4.2 软件设计

软件设计包括单片机软件与上位机软件设计。

单片机程序主要包括回波信号处理、采集以及传输。单片机程序流程如图6所示。

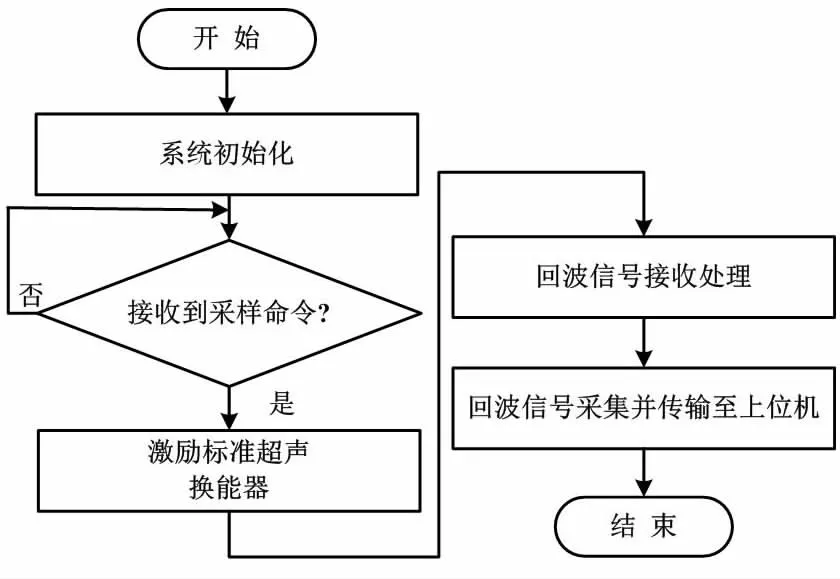
图6 单片机程序流程图

上位机采用Matlab软件进行编程。程序主要由串口通信模块、回波参数估计模块和超声换能器一致性匹配模块3个部分构成。超声换能器一致性匹配模块根据各超声换能器回波参数计算出欧式距离,并作为超声换能器的一致性判断标准,获得回波参数一致性较好的换能器配对以及显示其编号。

5 试验验证

超声换能器回波信号特征参数如表1所示。

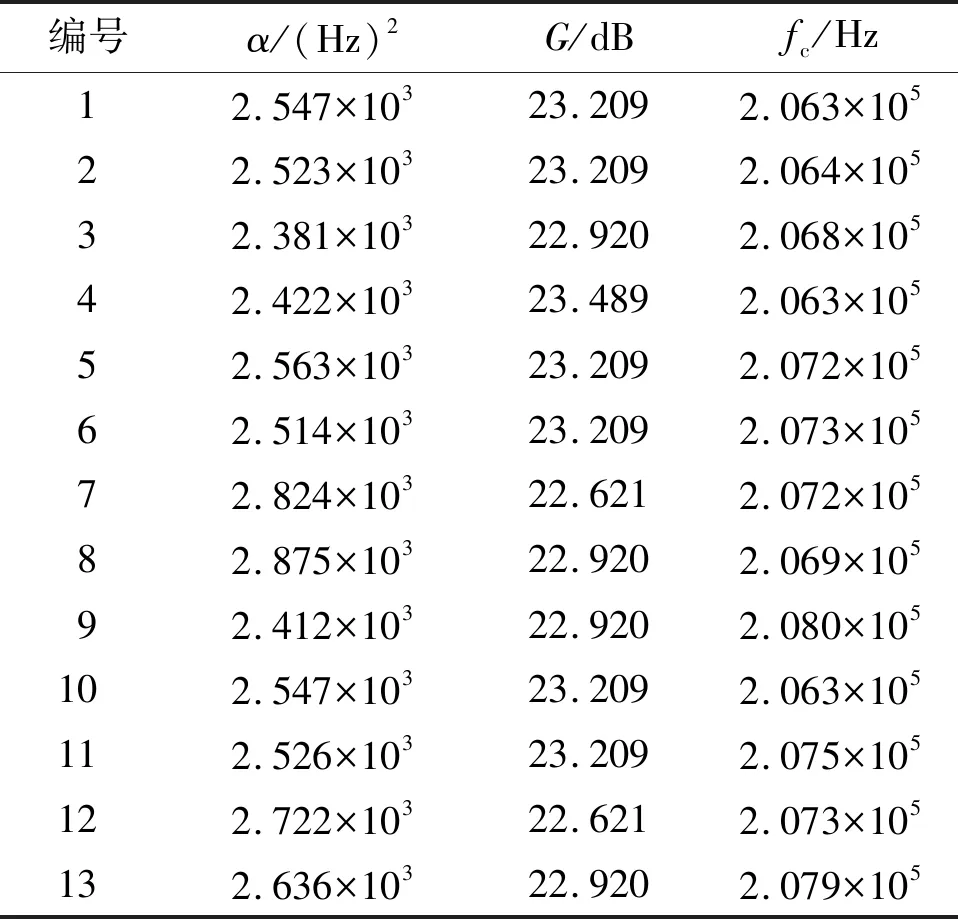
表1 超声换能器回波信号特征参数

本文选用编号为1～13号的共13只超声换能器进行动态性能测试。试验在温度为25 ℃、压力为101 kPa的空气环境下进行, 测量1～13号超声换能器的回波信号,并由人工鱼群算法得到回波信号特征参数。

由表1可知α、G、fc这3个特征参数的量级差距,因此在对换能器特征参数进行比较之前需要对参数进行归一化处理。

本文将被测超声换能器的带宽因子α合并为数组[α1,α2,…,α13],则α的归一化处理表达式为:

(7)

G和fc的归一化处理方法与α一致。

试验选取7号超声换能器,通过式(3)计算7号超声换能器与其他12个超声换能器的欧式距离。7号超声换能器与其他超声换能器的欧式距离如表2所示。

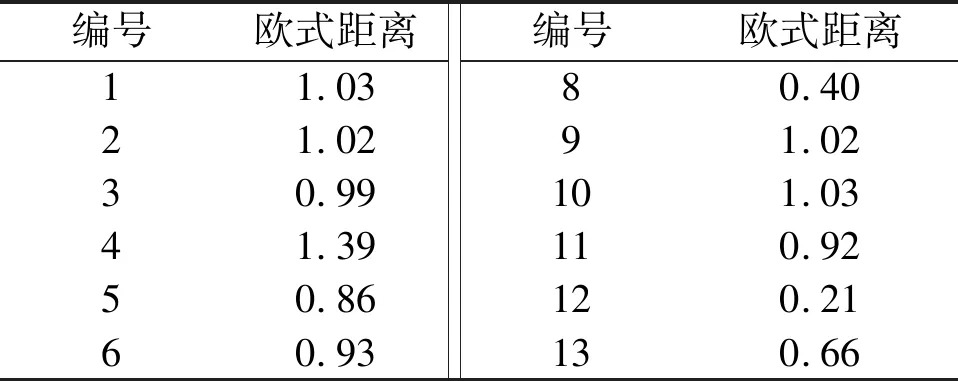
表2 7号超声换能器与其他超声换能器的欧式距离

由表2可知:7号超声换能器与12号超声换能器的一致性最好;7号超声换能器与4号超声换能器的一致性较差。因此,本文采用以上2组超声换能器分别进行流量测量试验。试验管径为DN50,安装角度为45°。试验流量测量装置为LQB-1000临界流文丘里音速喷嘴装置。装置的精度为0.3级,测量范围为0.9～2 500 m3/h。

按照《超声流量计检定规程》(JJG 1030—2007)要求[11],本文对2组超声换能器组成的流量计样机进行各流量点的重复3次流量试验。重复性的计算式为:

(8)

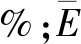
超声换能器流量测量结果如表3所示。

表3 超声换能器流量测量结果

由表3可知,动态性能较好的7号和12号这对超声换能器流量测量的误差和重复性优于动态性能较差的7号超声换能器和4号超声换能器。尤其在小流量的测量中,7号超声换能器和12号换能器的重复性更优。这是因为超声换能器的动态性能越接近,静态时差随工况变化和零漂越小,小流量测量的误差与重复性越好。

6 结论

本文提出了1种超声换能器动态性能测试方法。该方法根据回波信号的特征,首先建立回波信号的高斯模型,通过人工鱼群算法计算出高斯模型的最优特征参数;然后,将最优特征参数进行归一化,计算超声换能器间的欧式距离,以评价超声换能器的动态性能一致性。本文设计了超声换能器动态性能测试系统并进行相应试验研究。试验结果表明,动态性能一致性较优的超声换能器,其流量测量误差以及重复性均优于动态性能一致性较差的超声换能器。