融合MobileNetV3特征的结构化剪枝方法

刘 宇, 雷雪梅

(内蒙古大学 电子信息工程学院, 呼和浩特 010021)

近年来,深度神经网络(Deep Neural Network, DNN)已经成为解决各种计算机视觉任务的主要方法,例如图像分类[1]、目标识别检测[2-3]、语义分割[4-5]等.随着大数据时代的到来,数据集规模不断扩大,计算硬件图形处理单元(Graphics Processing Unit, GPU)的飞速发展使得前所未有的大型DNN模型可以被开发.深层的大型DNN模型虽然有较强的表达能力,但对计算和存储资源提出很多要求,导致其难以应用到硬件系统和移动设备中.为解决这些问题,模型压缩[6-7]得到快速发展.

目前主流的网络压缩方法有参数量化与共享[8]、低秩近似[9]、知识蒸馏[10]、设计轻量级的模型[11-16]和网络剪枝[17-26]等,其中网络剪枝是基于某种准则判断网络参数的重要性,删除冗余参数.针对网络剪枝, Yann等[17]和Hassibi等[18]最早提出用loss函数的Hessian矩阵来确定网络中的冗余参数,然而Hessian矩阵的计算本身就消耗大量时间.Han等[19]提出根据神经元连接权值的范数大小删除范数值小于阈值的连接.Chen等[20]提出HashedNets模型,该模型使用低成本的哈希函数实现参数剪枝.上述方法都是非结构性剪枝,修剪网络中权重小的不重要连接,得到的网络权值大多为0,因此可以利用稀疏格式存储模型来减少存储空间.然而这些方法只能通过专门的稀疏矩阵操作库或硬件来实现加速,运行时内存节省也非常有限.Li等[21]提出计算滤波器的L1范数,剪掉范数较小的滤波器.Chen等[22]提出使用Eyeriss处理器计算每一层能耗,优先删除能耗较大的层.Liu等[23]提出将批量归一化层(Batch Normalization, BN)的缩放系数γ作为判断滤波器重要性的依据,删除γ值小的滤波器.然而,这些方法只单独使用网络中的一部分参数,可能会导致对冗余参数的判定不够准确.韦越等[24]提出对模型进行稀疏化训练,然后将滤波器权重L1范数和BN层缩放系数γ的乘积作为判定依据.卢海伟等[25]提出将注意力机制和BN层的缩放系数γ相结合来判断滤波器重要性.上述方式可以更加准确地判断滤波器重要性.但相比于L1范数和注意力机制,Liu等[26]使用的稀疏性公式可以准确地表示卷积层中的提取到的参数信息.

为了适用于移动设备,出现了一些构造特殊结构的滤波器、网络层或网络具有存储量小、计算量低和网络性能好等特点的轻量级模型,如Mobile～Net[11-13]、Xception[14]、NestedNet[15]、MicroNet[16]等.其中,谷歌提出的MobileNetV1采用深度可分离卷积结构代替普通卷积操作,在参数量、计算量大幅度减少的同时,在ImageNet数据集上取得与视觉几何组(Visual Geometry Group, VGG)神经网络相当的准确率,得到学界的广泛关注.为提高准确率,MobileNet逐步从MobileNetV1发展到Mobile～NetV3,但模型体积越来越大,所需计算资源也越来越多,对移动设备中的资源要求越来越高.相较于传统DNN,轻量级网络设计更巧妙、结构更紧凑、计算方式更复杂,但可压缩的部分越来越少,给深度学习模型压缩的研究带来新的挑战.另一方面,不同轻量级模型具有不同网络结构特点,如何准确选择冗余结构,是对轻量级网络模型进行压缩的关键,是本文研究的主要目标之一.因此,为了进一步降低Mobile～NetV3对移动设备的硬件资源要求,使其可以部署到低功耗、低延时的应用场景中,基于Mobile～NetV3的网络结构特点提出一种新的模型压缩剪枝方法.

采用轻量级模型MobileNetV3-Large[13]与结构化剪枝相融合的方式,对网络进行压缩,提出一种新的剪枝准则.该方法令每个滤波器的稀疏值与BN层缩放系数相结合,从而对整体通道的重要性进行判别.首先,使用L1正则化对模型进行稀疏训练,然后利用稀疏性公式[26]和BN层缩放系数[27]得到滤波器的重要性函数,利用重要性函数作为判定依据,删除冗余滤波器.实验证明:在相同剪枝率的情况下,对比4种剪枝方式,本文的方法在压缩率相同的情况下具有更高准确率.

1 MobileNetV3

MobileNetV3[13]是谷歌在2019年提出的轻量级网络架构,除了继承MobileNetV1[11]和MobileNetV2[12]的特性之外,又拥有许多新特性.MobileNetV3使用的网络架构是基于神经网络架构搜索(Neural Architecture Search, NAS)实现的MnasNet,引入V1的深度可分离卷积、V2的具有线性瓶颈的倒残差结构和压缩激励模块(Squeeze and Excite,SE)结构的轻量级注意力模型,使用ReLU6函数和一种新的激活函数h-swish(x),如图1所示.图中:Dwise表示深度卷积,NL表示使用非线性激活函数,FC表示全连接运算,Pool表示下采样,hard-α表示NL激活函数的“hard”形式.该结构首先采用1×1点卷积对输入数据的维度进行扩充,然后进行逐深度卷积,再添加轻量级SE模块提升模型对通道的敏感度,最后使用1×1点卷积对维度进行压缩.其中V1的深度可分离卷积如图2所示,V2具有线性瓶颈的倒残差结构如图3所示.图中:C为滤波器层数(输入);k为卷积核大小;N为滤波器数量.在MobileNetV3-Large中基本网络单元占用大部分参数量计算量,具体如表1所示.MobileNetV3中使用ReLU6激活函数代替常规的线性修正单元(Linear rectification function, ReLU)函数,使激活函数输出参数分布的更加均匀[28],适合使用稀疏性公式进行判别.

表1 MobileNetV3-Large主要资源占用Tab.1 Main resource occupation of MobileNetV3-Large

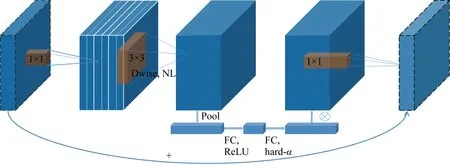
图1 MobileNetV3基本网络单元Fig.1 Basic network unit of MobileNetV3

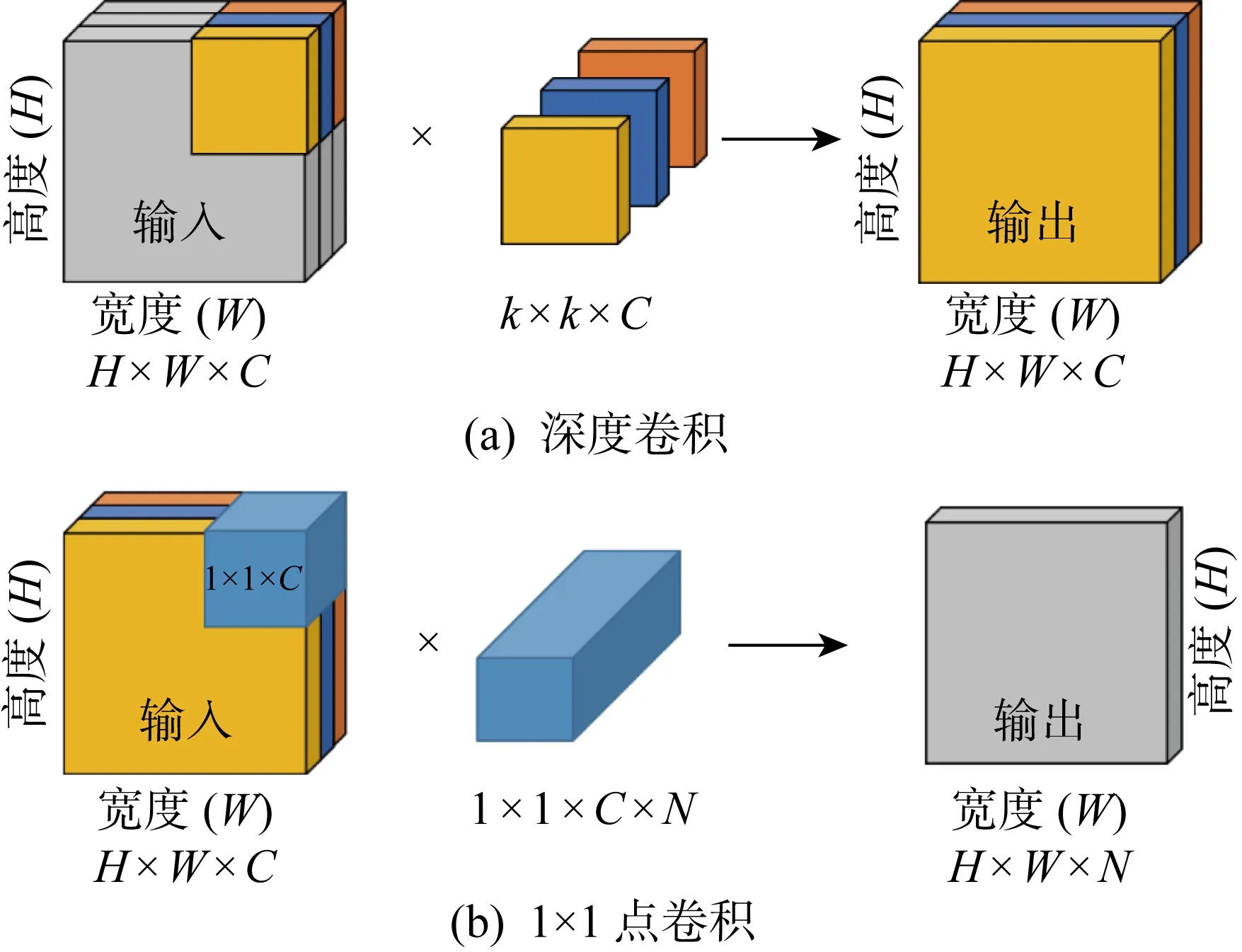
图2 深度可分离卷积示意图Fig.2 Depthwise separable convolution

图3 MobileNet-V2基本网络单元Fig.3 Basic network unit of MobileNet-V2

2 结构化剪枝方法

根据MobileNetV3的结构特点,在不破坏原始网络结构的情况下,减少卷积层滤波器可以大幅度减少网络的计算量和参数量,提高网络运算速度.因此,首先使用L1正则化对模型进行稀疏化训练,再利用卷积层和BN层两层的参数信息对网络进行修剪,提出将缩放系数和稀疏值的乘积作为滤波器重要性的判断标准,对网络进行以滤波器为最小单位的结构化剪枝.

2.1 稀疏训练

模型稀疏化是一种提升模型剪枝的有效方法,已有许多方法可使神经网络变得稀疏,不仅可以得到稀疏的网络参数,加快模型收敛速度,同时还可以保持网络精度,得到更紧凑的网络模型[29].稀疏化的方法有训练中使用稀疏表示[30]、稀疏代价函数[31]、稀疏正则化[32]等.

由于易于实现且不会对网络引入额外的开销,所以选择L1正则化对神经网络进行稀疏训练,惩罚一些不重要的参数,使得滤波器中的参数稀疏化.使用的损失函数如下:

L=LCE+λR(γ)

(1)

式中:LCE为交叉熵损失函数,对于特征缩放系数γ,R(γ)=|γ|;λ为一个超参数,λ越大惩罚的参数越多,BN层中的参数就会越接近0.

2.2 特征缩放系数

大多数卷积神经网络都使用BN[27]结构,它是一种可以实现快速收敛和更好泛化能力的标准方式,一般置于卷积层的后一层,对卷积层的输出进行归一化处理.BN层有两个可学习的参数γ和β,可以使特征值学习到每一层的特征分布.BN层输入输出关系如下:

(2)

式中:Zin和Zout分别为输入、输出;μc和σc分别为对应激活通道c的均值和方差;ε为一个添加到小批量方差中的常数,用于数值稳定性;β为对应激活通道的偏移系数.缩放系数γ与通道的激活程度一一对应,间接反映对应滤波器的重要性,可以作为判定滤波器重要性的依据,而且不会给网络带来额外开销.

2.3 稀疏性公式

基于Liu等[26]提出的稀疏性公式,根据下式计算滤波器稀疏值:

(3)

式中:n、c、w、h为组成卷积核4维张量的参数,n为滤波器数量(输出),c为滤波器层数(输入),w和h分别为滤波器宽度和长度;n,c,w,h为正整数且n∈[1,N],c∈[1,C],h∈[1,H],w∈[1,W];σ(x)为公式Sl(n)中的一个变量,用于计算Sl(n);kl,nchw为卷积核权重.Sl(n)表示第l层中第n个滤波器的稀疏性,如果一个滤波器有越多系数小于该层的平均值Ml,那么Sl(n)越接近0,表示该滤波器与该层的其他滤波器相比更冗余.Ml是一个阈值,式(3)中Ml表示第l层卷积核权重平均值,根据下式计算:

(4)

相比于每个滤波器的L1范数平均值,以所有滤波器权重范数和的平均值Ml作为Sl(n)的阈值,计算每个滤波器的稀疏值,更能体现每个滤波器在整个网络中的重要性.前者通过一个滤波器中的参数判定滤波器重要性,后者通过整个网络中所有滤波器的参数来判断一个滤波器对整个网络的影响,后者不仅更加准确,也更适合全局阈值修剪网络的方法.

2.4 滤波器重要性判定依据

利用卷积层的参数Sl(n)和BN层参数γ两部分结合,作为滤波器重要性的判定依据,得出重要性判定函数如下:

mi=γiSi

(5)

式中:mi为第i个滤波器的重要性评分;γi为第i个滤波器对应的BN层缩放系数;Si为利用式(3)计算出的第i个滤波器的稀疏值.

根据重要性判定依据mi对网络进行修剪.图4是本文使用的剪枝方法图,具体步骤如算法1所示,其中d表示权重的维度,一般情况下为4.

图4 结合Sl(n) 与缩放系数γ的结构化剪枝方法图Fig.4 Structured pruning method combining Sl(n) and scaling factor γ

算法1本文使用的剪枝方法

1: 使用随机权重W0∈Rd初始化一个网络,初始化剪枝掩码θ=1d.

2: 作用参数λ训练W0共200次,得到权重W1.

3: 从W1中计算mi,按顺序排列mi得到一个索引index.

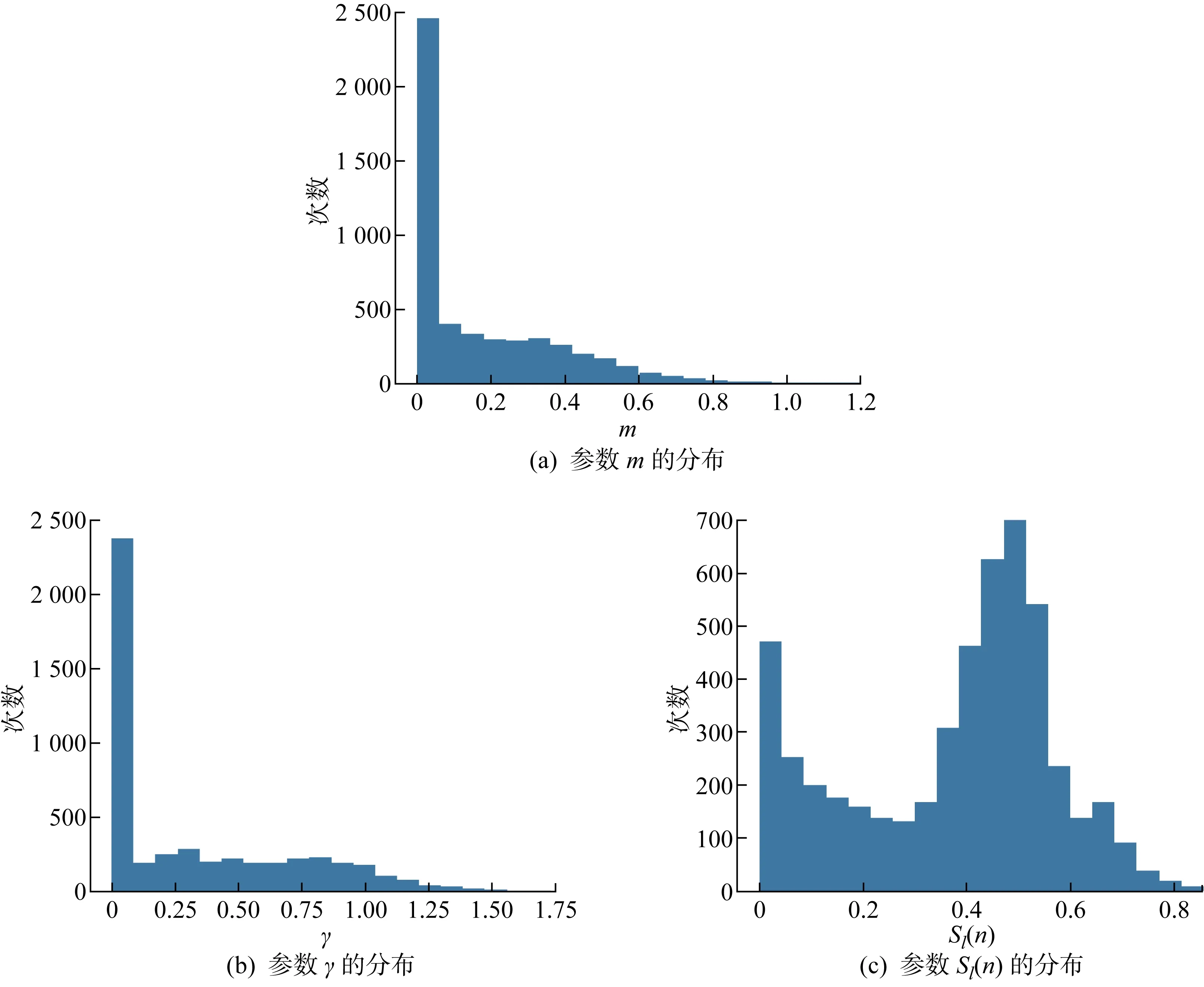
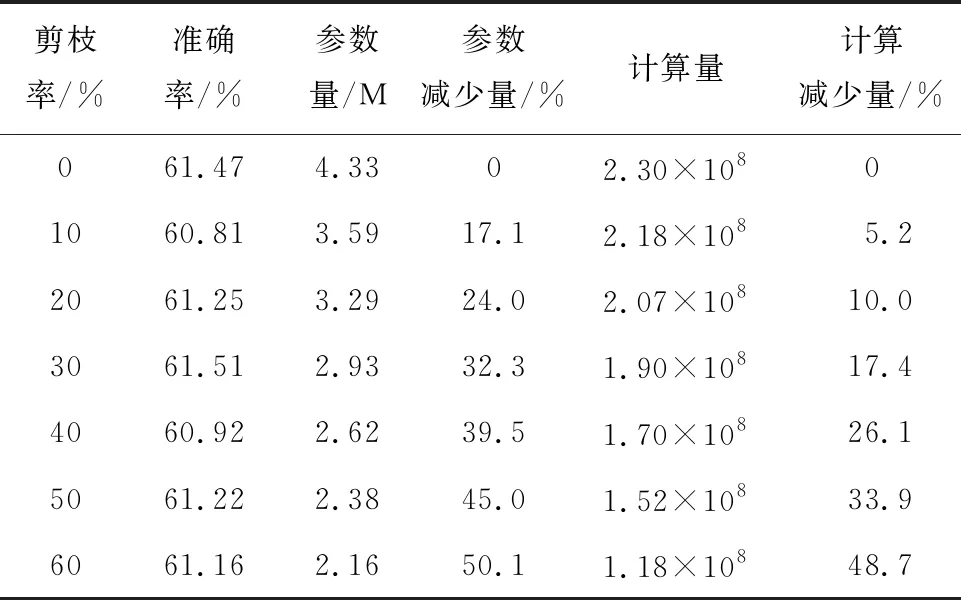
4: 当mi

5: 如果W2中的滤波器权重等于0,则删除滤波器.

6: 得到紧凑的权重参数W3,对应新的网络结构.

7: 重新训练W3共150次,得到最终结果W4.

在MobileNetV3特殊的网络结构中,倒置的残差模块占用大部分运算量和内存,因此本文主要对MobileNetV3 的基本网络单元结构进行修剪.由于深度可分离卷积中深度卷积的存在,要求这层卷积运算输入和输出的滤波器个数一致,但直接裁剪会导致输入和输出滤波器个数不一致,网络无法运行,而且深度可分离卷积中主要的计算量和参数量都来自于1×1 点卷积,深度卷积只占用很少的资源,所以只需要裁剪网络单元中的1×1卷积的滤波器,间接影射到深度卷积和后续的运算,就可以最大幅度减少网络的参数量和计算量.具体对模型的裁剪如图5所示,其中虚线部分表示裁剪的滤波器,首先裁剪1×1滤波器的个数,进而影响3×3滤波器维度和最后的1×1滤波器维度,灰色部分为裁剪滤波器后减少的对应特征图.

图5 在MobileNetV3上剪枝后的结构图Fig.5 Structure of MobileNetV3 after pruning

3 实验

3.1 实验环境

为保证实验的准确性和客观性,使用经典数据集CIFAR-10和CIFAR-100作为实验数据集.CIFAR-10是一个10分类数据集,每个类包含 6 000 张图片,共有 60 000 张彩色图片,其中 50 000 张作为训练集,10 000 张作为测试集,图片分辨率为32像素×32像素,在实验过程中将图片调整大小为224像素×224像素.CIFAR-100是CIFAR-10衍生出来的数据集,区别是CIFAR-100数据集包含100个分类,每个类包括600张图片.使用NVDIA GeForce RTX 3060 6 G显卡,采用Pytorch深度学习框架进行搭建、训练和测试.实验过程中使用Adam优化器,初始学习率为0.001,正则化系数选择 105对模型MobileNetV3-Large进行稀疏训练,初始训练迭代200次,微调 150次,微调时不进行稀疏训练.

3.2 实验结果与分析

3.2.1正则化系数的选择 综合考虑准确率和稀疏化效果,为了找出最恰当的正则化系数λ,对网络进行稀疏化训练时,同时设置多个λ,评估不同λ对模型准确率和稀疏化的影响.在实验过程中发现L1正则化系数λ大小不同基本不影响Sl(n)的分布,但会导致BN层参数γ分布不同,如图6所示.当λ=0时,BN层参数γ近似正态分布,当使用γ作为其中一个判定标准对模型进行剪枝时会删除部分有用的参数信息,影响剪枝效果.而随着λ增加,越来越多的参数γ聚集在0附近,对于模型剪枝而言,可以更加准确地判断冗余滤波器.因此,在选择BN层系数作为其中一个滤波器判定标准时,稀疏化训练至关重要.

图6 不同正则化系数下的γ值分布图Fig.6 γ value distribution at different regularization coefficients

不同的正则化系数λ对网络参数的约束程度不相同,网络准确率也不相同.越大的正则化系数会惩罚越多的参数,使滤波器参数越稀疏.但是惩罚过多的参数对网络的准确率也有很大的影响,参数越稀疏,网络准确率也会越低.λ=0,10-3,10-4,10-5,10-6时,对应的准确率分别为88.28%、85.50%、87.22%、88.15%、88.15%.λ大于10-3时,网络中参数过于稀疏,导致模型不收敛;λ小于10-3时,模型精度与稀疏程度会有一个折中.综合准确率和稀疏程度两种指标,选择10-5作为正则化系数,在保持准确率不变的情况下,对滤波器参数进行约束.

3.2.2重要性评分 经过正则化训练之后,确定了正则化系数λ后,通过确定对应的γ、Sl(n)可以得出相应的重要性评分m,分布规律如图7所示,不同剪枝率下对应的m的值及γ和Sl(n)的范围如表2所示.由图7可知,γ、Sl(n)两个参数相对独立,m可以更准确地判别滤波器的冗余程度.

表2 不同剪枝率下对应的m值及γ和Sl(n)的范围Tab.2 m,γ, and Sl(n) at different pruning rates

图7 正则化训练后的参数分布(λ=10-5)Fig.7 Parameter distribution after regularization trainning (λ=10-5)

3.2.3剪枝率 使用全局阈值对网络进行一次性剪枝.为了寻找最合适的剪枝率,设置14个不同的剪枝率在CIFAR-10数据集上对MobileNetV3-Large进行测试.由于裁剪到70%时会删除某个层的所有滤波器,导致网络结构被破坏,所以将剪枝率设置在0%～60%.模型在剪枝45%时,重新训练准确率最高达到88.82%,比没有剪枝前稀疏训练的模型高0.67%,比未剪枝未稀疏训练的模型高0.54%,说明本文剪枝方法减少部分影响判断结果的无用参数,减少神经元之间错综复杂的依赖关系,增强模型的泛化能力,提高模型的鲁棒性.不同剪枝率下模型参数量和计算量对比如表3所示.

表3 不同剪枝率下参数量计算量Tab.3 Parameters and FLOPs at different pruning rates

3.2.4不同剪枝方法对比 为了进一步说明本文剪枝方法的有效性,在同一实验环境,尽可能压缩网络且保存网络精度的条件下将全局剪枝率设置为50%,在CIFAR-10上测试对比4种剪枝方式, 实验结果如表4所示.在剪枝率相同的情况下,本文剪枝方式准确率略高于其他方式,同时在参数量和计算量上也有很大程度的压缩.在剪枝率50%的情况下,参数量下降44.5%, 计算量下降40.0%, 准确率上升0.4%.

表4 几种剪枝准则在CIFAR-10上的对比(裁剪50%)Tab.4 Comparison of several pruning criteria on CIFAR-10 (50% pruned)

实验结果表明,在相同剪枝率的情况下本文的剪枝方法获得较好的剪枝结果,与单独使用BN层参数γ和单独使用卷积层参数相比,本文将两者结合的方法对冗余滤波器判别更加准确,获得更高的准确率和参数压缩率.

3.2.5剪枝前后模型结构可视化对比 图8为MobileNetV3-Large网络剪枝前后对图像特征提取的热力图,由于使用CIFAR-10数据集训练网络,所以选择数据集中的猫和狗两个分类,在网络上随机选取两张图片.首先原始网络抓取到很多的特征,当对网络逐步裁剪10%时,网络删除了大部分特征,此时网络准确率最低(见表3),这表明网络删除少量冗余信息,但微调过程中又扩大其他冗余信息.随着冗余信息删除越来越多,直到裁剪40%时,网络微调后开始获得越来越多特征信息,网络精度也在上升,同时网络结构也越来越小,表明此时网络得到最优的网络结构和参数信息.当网络再进行裁剪到50%时,网络抓取的特征又会逐渐减小,网络精度开始下降.

图8 剪枝前后模型结果可视化对比Fig.8 Comparison of visualization of model result before and after pruning

从结果上来看,裁剪网络结构会减少网络中提取到的部分特征,但使用剩余特征进行网络微调可以让剩余特征学习到比原始网络更多的特征,也即突出了剩余特征.这里的剩余特征也就是最开始网络判定的重要特征.因此网络准确率保持不变甚至优于原始网络,也表明本文剪枝方法可以准确地判断冗余信息.

3.2.6剪枝后的模型 在不改变模型整体结构的情况下,保持准确率基本不变所能达到的最大剪枝率为50%,为了进一步说明剪枝后模块中的滤波器变化情况,对比剪枝前[13]和剪枝后模型每层滤波器个数,如表5所示.由于主要对block模块进行裁剪,所以主要影响模块中通道数.bneck表示使用MobileNetV3的主要结构单元,激励模块表示在bneck中加入Squeeze-and-Excite模块,HS和RE分别为激活函数H-swish和ReLU6,NBN表示卷积层后不加入BN层,—表示没有这部分结构,√表示有结构,q表示网络输出分类数.

表5 剪枝前后模型通道数对比Tab.5 Comparison of model channels before and after pruning

3.2.7在CIFAR-100上进行测试 为了进一步证明本文剪枝方法的有效性,在标准数据集CIFAR-100上进行测试,将剪枝率设置为0%～60%,实验结果如表6所示.

表6 不同剪枝率下参数量计算量(CIFAR-100)

4 结语

基于深度神经网络压缩理论,采用结构化剪枝对轻量级模型MobileNetV3-Large进行压缩.在保证网络精度略有上升的情况下,对模型中的滤波器进行修剪,达到压缩网络的效果.提出一种判断滤波器重要性的方式,利用稀疏性公式和BN层缩放系数γ的乘积作为判断滤波器重要性的准则.实验证明:一方面,计算滤波器的稀疏性信息可以提取到具有判别性的信息;另一方面,特征缩放系数γ也衡量了滤波器重要性.综合两种判断指标,证实本文的判定方式能够更加准确地选取冗余滤波器,在模型准确率基本保持不变的情况下,实现模型最大程度上的压缩,提高网络的泛化能力.