双馈风电场抑制电网低频振荡的自适应附加控制策略
刘新宇, 王 森, 曾 龙, 原绍恒, 郝正航, 逯芯妍
(1. 华北水利水电大学 电力学院,郑州 450011; 2. 广东工业大学 自动化学院,广州 510006;3. 贵州大学 电气工程学院,贵阳 550025)
现代工业的迅猛发展已经造成对煤和石油等化石能源的过度依赖和严重的环境污染等一系列问题.由于风力发电(简称风电)不会污染环境且风能属于可再生能源,风能的充分利用对能源结构的调整和实现“双碳”目标具有重要意义.近些年,伴随着大规模风电并网的快速发展,建设更大规模的风电场以及远距离输电问题应运而生[1].由于风能具有随机、不稳定的特点,而我国的用电负荷中心往往距离风电场比较远,输电线路负荷较重,加之风电场又处于相对薄弱的电网末端,所以给风电并网系统的稳定性造成较大影响[2].
大规模的风电并网、长距离的输送线路、风能不稳定这些问题大大降低了系统的阻尼,因此当系统发生跳闸、三相接地短路或是小扰动干扰时,易引起传输线路的功率低频振荡.迄今为止,已经发现多次电力系统低频振荡现象,给电力系统带来很大影响.在国内,随着中国新疆维吾尔自治区北部地区风电装机容量的迅速增加,自2014年6月以来,广域测量系统已反复捕获次同步频率下的持续功率振荡[3].在国外,德克萨斯电力可靠性委员会电网中已经发现多次4 Hz的低频振荡[4].在此类严重事故中,低频振荡甚至会激起附近涡轮发电机的强烈扭转振动,从而导致发电厂的所有发电机跳闸.因此,有必要增强包含风电的混合电力系统的阻尼,以提高系统频率稳定性.
为保证风电并网系统稳定安全运行,很多国家已经出台相关的政策规定在风电机组中必须带有可以增强系统阻尼的附加环节.文献[5]中提出基于区域极点配置的风电系统弱阻尼低频振荡抑制控制策略,采用线性矩阵不等式的区域极点配置方法设计反馈控制器,将系统中的弱阻尼振荡模式配置到所控制区域,提高系统的阻尼比.文献[6]中以系统的频率偏差值作为输入,根据不同的风速设置桨距角,设计基于变系数的下垂控制调节风力发电机的有功出力,为系统注入正阻尼.文献[7]中根据两区域电力系统模型,选择合适的输入输出变量,对输入函数和状态函数求导得到反馈控制律,提出基于非线性控制算法的附加阻尼控制策略,可以有效地处理阻尼控制器中的非线性环节.文献[8]中将双馈风力发电机(DFIG)和电力系统静态稳定器(PSS)放在一起,建立系统的状态方程,定义系统振荡模式对传递函数的灵敏度,然后运用定义的灵敏度优化控制参数,该控制策略能有效抑制系统低频振荡.文献[9]中分析含DFIG的风电系统可能会引起低频振荡的原因,对比基于复转矩系数法的4种控制策略,为开发最优控制策略以抑制DFIG系统在不同条件下的轴系振动提供了参考.文献[10]中提出一种有源-无源协调双通道功率调制阻尼控制器,该控制器可以较好地发挥DFIG转子侧控制器的阻尼控制能力.文献[11]中提出基于电力系统稳定器和功率振荡阻尼器的鲁棒协调控制策略改善低频振荡阻尼,该方法使用改进的基于特征值的目标函数实现,并用灰狼优化器进行优化.文献[12]中提出基于阻耗系数的附加阻尼模糊控制策略,通过控制转子侧换流器调节DFIG无功功率来增强系统阻尼,进而抑制系统低频振荡.文献[13]中提出一种基于主动抗扰控制的有功无功附加阻尼控制器,能起到很好的抑制负阻尼的作用.文献[14]中提出一种基于自抗扰控制器的广域阻尼控制器协调优化策略,采用人工蜂群算法对自抗扰控制器和广域阻尼控制器进行协调优化,提高系统阻尼水平.文献[15]中设计基于频率反馈的大规模柔性负荷控制策略和统一潮流控制器串联侧功率反馈附加控制策略,最后运用遗传算法优化协同控制参数,得到最优控制策略.文献[16]中分析有功功率环节和无功功率环节附加阻尼控制的差异,提出一种基于bang-bang调制的混合快速阻尼控制策略和基于二阶滑模的双馈风电机组鲁棒阻尼控制策略,对电力系统区间振荡有很好的抑制效果.文献[17]中利用状态反馈的方法将系统输入、输出作线性化处理,将非线性系统线性化,最后提出基于超螺旋算法的阻尼控制器,该控制方法不依赖于系统的详细建模参数,具有良好的工程应用价值.
综上所述,国内外学者针对电力系统区域间功率低频振荡已经进行了深入的研究,也提出大量的附加阻尼控制器设计方法.然而,大多数设计方案将系统中联络线功率或发电机功角偏差等参数作为输入,忽略系统平衡点变化后的动态特性对低频振荡的影响,在系统平衡点附近线性化的基础上设计类似于PSS结构的附加阻尼控制器,而很少有研究将DFIG自身转子电压和磁链的关系应用到阻尼控制器设计上.本文对DFIG的动态频率响应和转子励磁电压与磁链之间的关系进行研究,结合终端滑模变结构控制的思想,设计基于转子磁链偏差的快速终端滑模附加阻尼控制器,并证明该系统的收敛性和稳定性.该控制器将磁链的偏差作为输入,输出一个附加信号到转子侧功率控制环节,进而控制转子侧换流器,调节DFIG出力,抑制系统低频振荡现象.最后,通过仿真验证本文所提控制方法对系统低频功率振荡的影响.
1 DFIG响应阻尼调节能力分析
DFIG系统在三相静止坐标系中的模型阶是一个多变量、高阶次、强耦合、非线性的复杂时变系统.为了便于计算和控制,运用坐标变换将其转换到两相同步旋转d-q坐标系下进行分析[18].忽略定子绕组压降和电磁暂态变化过程,将定子电压定向于d轴上,DFIG定子输出有功功率(Ps)、无功功率(Qs)和转子磁链方程可表示为
(1)
式中:Ls、Lr、Lm分别代表定子自感、转子自感和定转子互感;ω1为同步转速;ψqs为d-q坐标系下定子q轴磁链分量;ψdr、ψqr分别为d-q坐标系下转子磁链分量.
(2)
式中:Rr为转子电阻;ωs=ω1-ωr为发电机转差角速度,其中ωr为发电机转子转速;udr、uqr分别为转子d-q轴电压分量;Ug为电网侧电压.


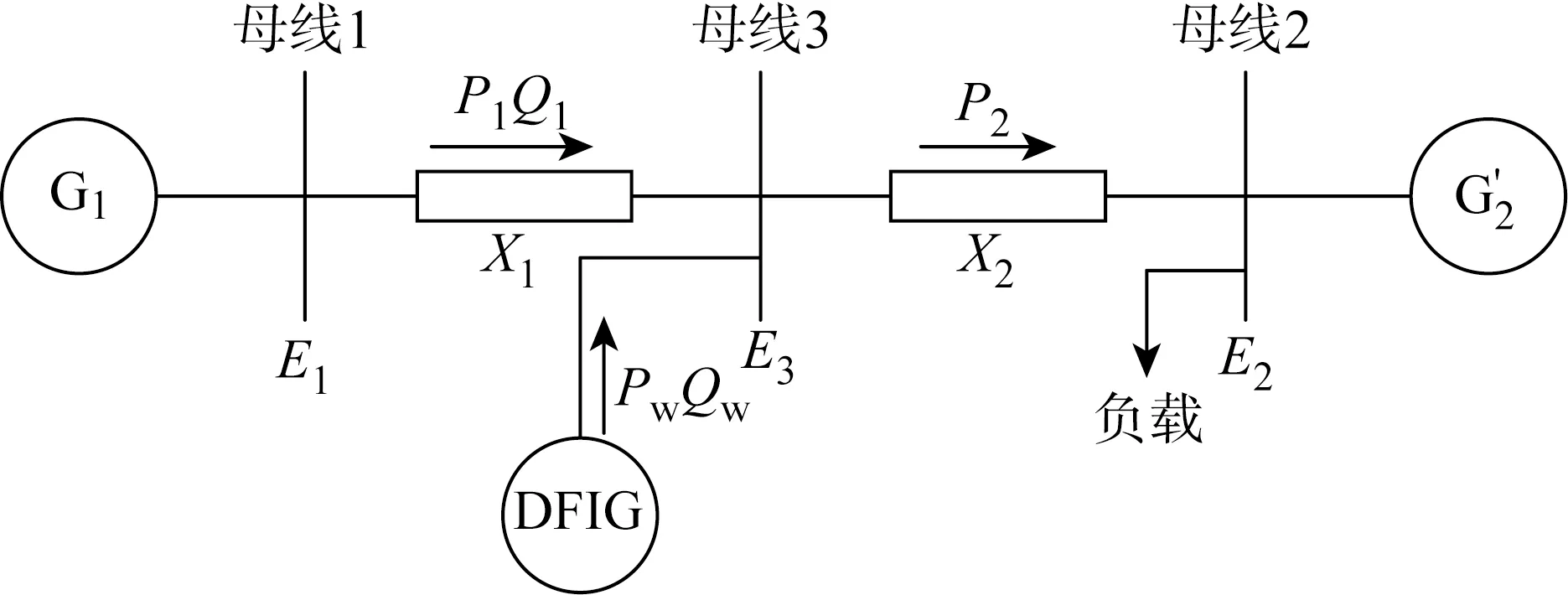
图1 两区域电力系统模型Fig.1 Two-region power system model
2 终端滑模附加控制器设计
由上述分析可知,调节DFIG输出有功功率可以提高系统的阻尼水平,因此可以通过调节DFIG的有功功率改善系统阻尼水平,进而抑制系统区域间的低频振荡.
2.1 系统滑模面与控制律设计
由式(2)可得,DFIG运行过程中,转子外加电压和转子磁链之间的关系如图2所示.图中:s为DFIG转差率.DFIG在发电状态时,将转子磁链分量ψdr、ψqr作为系统的受控输出,则转子励磁电压udr、uqr为系统的控制输入.为达到系统快速控制的目的,将终端滑模变结构控制方法运用到DFIG转子磁链控制方案之中,设计转子磁链控制器,使系统磁链跟踪期望磁链,确保系统在指定时间内迅速达到稳定状态.

图2 DFIG转子外加电压与磁链之间的关系图Fig.2 Relationship between applied voltage and flux linkage of DFIG rotor
(3)
基于以上分析,设计如下滑模面:
(4)
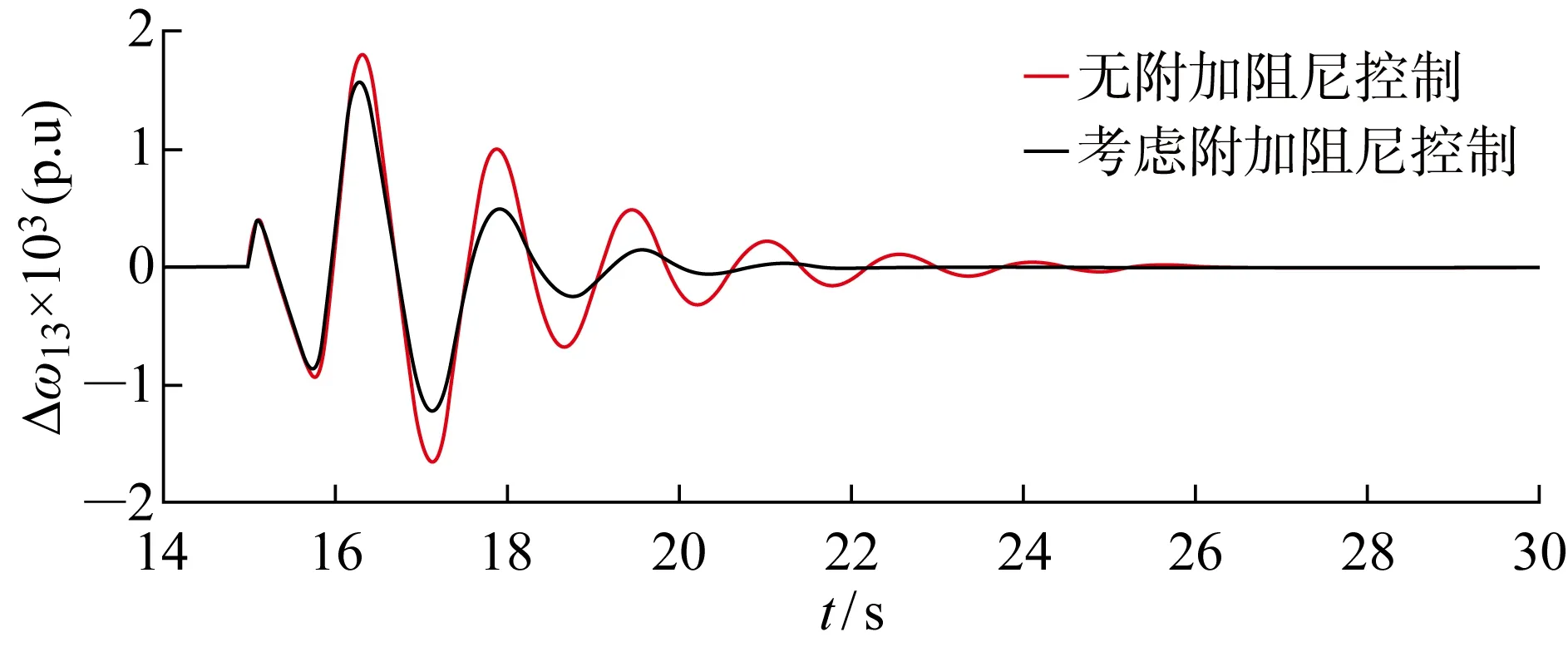
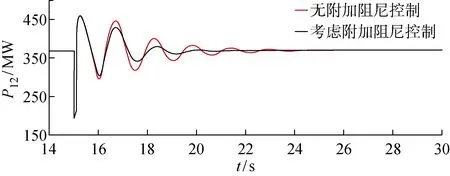
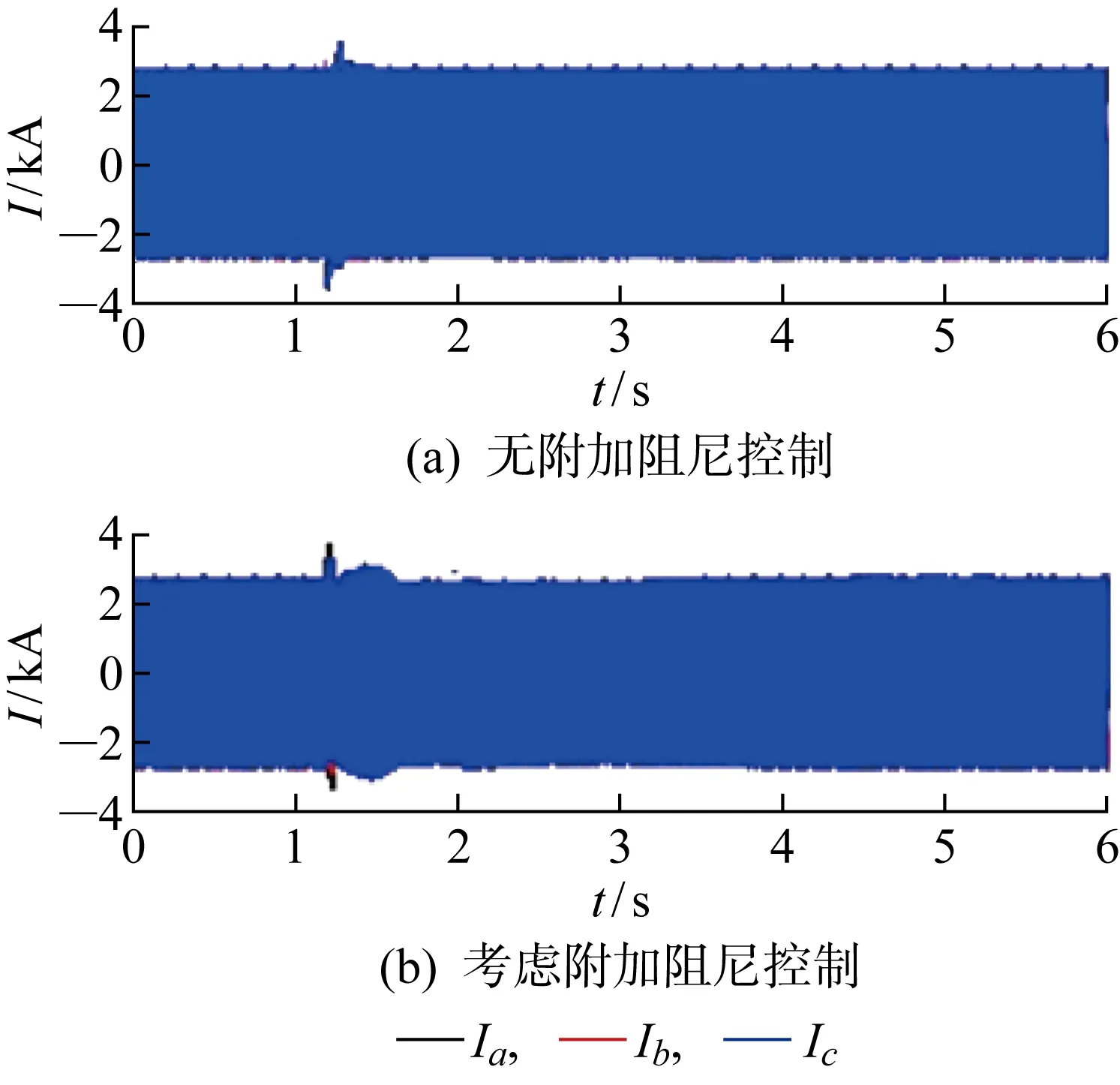
式中:参数ρ1>0;p1、q1为正奇数,且0 式(4)对时间求导得: (5) 将式(3)代入式(5)得: (6) 则转子d轴磁链采用的控制律可设计为 udr=udreq+udrn (7) 式中:udrep、udrn分别为等效控制律和切换控制律,且满足 (8) (1) 系统收敛性证明. 证明当Sd=0时,系统位于滑模面上,此时有 (9) 求解可得: (10) 则DFIG的d轴磁链状态可在有限时间Δtd内快速收敛到0,证毕. (2) 系统稳定性证明. 证明取李雅普诺夫函数: V(t)=Sd(t)/2 (11) 求导可得: (12) 将式(6)代入式(12)可得: (13) 所以V(t)≤0,系统在李雅普诺夫稳定性理论上全局渐进稳定,证毕. 同理可得转子q轴磁链控制律为 uqr=uqreq+uqrn (14) (15) 式中:参数ρ2>0;p2、q2为正奇数,且0 图3 机侧控制器模型Fig.3 Control model of machine side 系统中使能环节表达式如下: (16) 根据前文推导的快速终端滑模附加控制的原理设计附加阻尼控制器,在MATLAB/Simulink中建立如图4所示的四机两区域模型并进行仿真分析.图中:G2、G3和G4为同步发电机,L1、L2分别代表区域1和区域2负荷. 仿真环境设置:设t=15 s时,两区域联络线发生0.1 s的三相短路,此时系统由于阻尼不足,在联络线上发生功率振荡;t=15.1 s时故障消除,系统恢复正常运行状态.观察无附加阻尼控制下和本文提出的附加阻尼控制策略下系统中各项参数的响应曲线. 图5为同步发电机转速振荡曲线.图中:ω为转速.对比有、无附加控制的响应曲线可知,在考虑附加阻尼控制情况下的同步发电机转子转速响应曲线的振幅更小,更快趋于稳定,具有更好的阻尼特性.由图6所示的同步机G1和G3转子角速度的差值(Δω13)振荡曲线可知,在考虑附加阻尼的情况下,G1和G3转子角速度偏差振荡的振幅和时间均减小.说明所提出的附加控制策略对系统同步发电机的振荡有一定抑制作用. 图5 同步发电机转速变化曲线Fig.5 Speed curves of synchronous generator 图6 同步发电机G1和G3转子角速度偏差振荡曲线Fig.6 Angular velocity deviation oscillation mode of synchronous generator G1 and G3 图7为DFIG转子励磁电流(Ir)的变化曲线.对比图7(a)和7(b)可以看出,当系统发生低频振荡时,在有附加阻尼控制情况下,故障期间DFIG转子电流增大并有一段时间的振荡响应,使DFIG及时发出有功功率支撑电网;在没有附加阻尼控制情况下,故障期间DFIG转子电流变化较小,不能很好地响应系统振荡.图8为两区域联络线功率(P12)变化曲线,从图中可以看出在考虑了附加控制的情况下,联络线功率振荡的振幅明显减小,并且更快地趋于稳定. 图7 双馈发电机转子电流变化曲线Fig.7 Rotor current curves of DFIG 图8 联络线功率振荡曲线Fig.8 Power oscillation curves of transmission line 图9为DFIG定子电流(Is)变化曲线.由图可知,在无附加控制下,故障期间DFIG定子电流几乎没有变化.而在采用附加控制时,故障期间定子会短时振荡现象,但其电流值仍在安全范围之内,说明所提的附加阻尼控制策略在及时调节有功功率输出的同时,并不会对双馈风电系统带来负面影响.图10为DFIG有功功率(Pw)响应曲线.从图中可以看出,在没有考虑附加控制情况下,系统发生低频振荡之后,DFIG有功功率并没有响应系统振荡,而在考虑本文所设计的附加阻尼控制情况下,DFIG有功功率输出能快速做出动态响应以提高系统的阻尼水平来抑制低频振荡. 图9 双馈发电机定子电流响应变化Fig.9 Stator current curve of DFIG 图10 DFIG有功输出振荡曲线Fig.10 Response curves of DFIG active power 为了充分验证所提附加控制策略在工程应用上的可行性,开发基于RTDS的风电并网四机两区域实时仿真系统,主要仿真参数和离线仿真参数相同. 在RTDS平台实验中,系统运行至t=1.2 s时,在两区域联络线上设置三相瞬时短路故障,传输线路出现功率低频振荡现象;t=1.4 s时,去除故障;监测DFIG定子电流、转子电流和有功输出响应情况以及系统振荡频率在是否考虑附加阻尼两种情况下变化曲线,结果如图11~14所示. 图11 系统频率变化曲线Fig.11 Frequency change curves of system 图11为系统频率(f)响应曲线.从图中可以看出,在系统发生低频振荡故障期间,无附加阻尼控制情况下的系统频率衰减较慢,振荡持续时间相对较长.而采用所提附加控制之后,系统频率振荡曲线衰减较快,且振荡的幅值更低,系统整体表现出更好的阻尼特性.图12为DFIG有功出力响应曲线.由图可见,当联络线发生功率振荡时,如果考虑附加控制,DFIG就可以及时输出更多有功功率响应其振荡,为系统提供更多阻尼. 图12 DFIG有功出力变化曲线Fig.12 Active output oscillation curves of DFIG 图13为转子励磁电流实时仿真曲线.图中:I为电流;Ia、Ib、Ic分别为abc三相电流.对比实验结果可知:在采用附加阻尼控制策略的情况下,在故障期间,转子励磁电流增大,以便使双馈发电机及时发出更多有功功率;而无附加阻尼控制下,转子励磁电流在故障期间几乎没有变化.而且从图14可以看出,定子电流实时仿真结果与离线仿真时的动态响应曲线一致,均能够保证DFIG的安全运行. 图13 DFIG转子电流变化曲线Fig.13 Rotor current curves of DFIG 图14 DFIG定子电流变化曲线Fig.14 Stator current variation curves of DFIG 研究风电功率调节对系统低频振荡抑制问题,在DFIG的机侧电流控制环上引入以增加电力系统阻尼为目标、基于李雅普诺夫稳定性理论的快速终端滑模附加阻尼控制器.利用MATLAB仿真测试与实验验证,在电力系统出现低频振荡故障时,所提出的快速终端滑模控制不仅可以快速调节DFIG有功功率,提高系统的阻尼水平,有效抑制低频振荡;而且在系统响应过程中,风力发电机的有功功率响应速度快、变化平滑,定子电流振荡持续时间很短且振荡幅值在安全范围内,不会影响风电场安全运行,具有一定的应用参考价值.
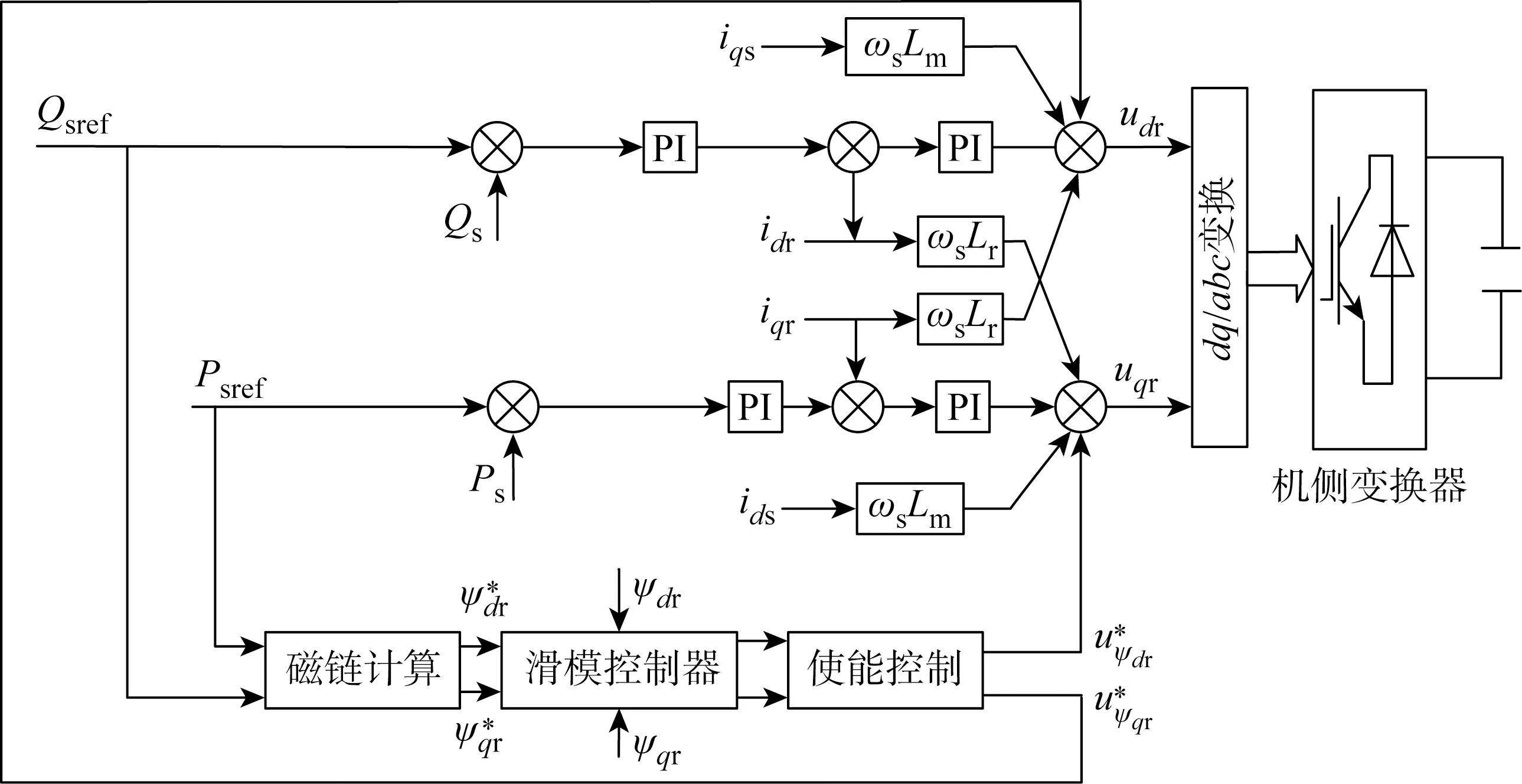
2.2 系统收敛性与稳定性分析

3 系统离线仿真与分析





4 系统实时仿真实验验证与分析



5 结语

