机器学习背景下中国股票市场繁荣度预测

刘美欣

(中国社会科学院大学 经济学院，北京 102488)

股票市场可预测性一直以来是金融领域的研究重点。越来越多的研究表明，很多变量能够显著预测未来股票市场收益率，并已构建出各种股票特征以预测个股收益率。近几年世界经济长期停滞，各大经济体争相使用宽松的货币政策以刺激经济增长，导致资本市场流入了过多资金并且长期繁荣，中国经济有脱实向虚趋势，未来的股票市场如何发展是一个值得探讨的问题。

1 机器学习算法概述

随着机器学习算法预测表现的提升，以及大数据时代实证资产定价领域数据可获得性的提升，用机器学习预测个股收益率是当下一个非常活跃的领域。机器学习模型已在微观金融领域被广泛应用并被证实有更好的预测表现。机器学习模型主要有降维、惩罚项和非线性等方面的优势，可以在预测过程中得到更好的效果。在大数据的应用过程中，降维方法可以在尽量多地保证信息完整的情况下压缩特征值，使得特征分析更为容易，常见的降维方法主要是主成分分析；机器模型存在的一个问题是过拟合，即模型学习到过多的样本特征，而非整体特征，导致预测误差，此时可以通过引入惩罚项来避免问题；当前许多的计量模型主要是线性模型，但现实中的问题大多是非线性的，机器学习中典型的非线性模型，如神经网络和树模型可以更好地拟合这种非线性问题，从而得到更优的效果。

Gu et al.(2020)是机器学习在实证资产定价领域的代表作，其首次证明了用机器学习算法预测个股收益率可行。作者使用900+个特征作为输入变量，比较了13种机器学习算法的预测表现，并根据个股的预测表现构造多空投资组合检验资产组合的收益率。结果表明：用机器学习算法预测个股收益率可以得到更高的样本外预测表现以及更高的经济收益。Leippold et al.(2021)等借鉴Gu et al.(2020)的方法，对机器学习在中国A股市场的应用进行了检验。结论均显示，机器学习算法对于个股收益率的预测表现显著优于传统方法。林辉等(2022)将机器学习算法应用于衍生品和大类资产；范小云等(2022)使用机器学习算法从文本信息中提取出有用信息提高预测表现；方毅等(2022)比较了不同机器学习算法对股票收益率的预测表现。综上所述，已有大量文章将机器学习算法应用于个股收益率预测，但少有文章对股票市场繁荣度进行预测。

宏观经济现象及变量间的影响是交互的、非线性的，文章借助机器学习算法探究宏观经济变量对中国股票市场繁荣度的影响及可预测性。借鉴已有研究，文章主要探究三个问题：①股票市场繁荣度是否是可预测的；②何种模型的预测表现最好；③哪些特征对模型预测表现贡献最大。

2 机器学习算法理论介绍

文章采用Gu et al.(2020)对机器学习的定义，其将机器学习定义为“一系列服务于统计预测的高维模型，以及与之相伴的用于模型选择和防止过拟合的正则化方法和对大量候选模型设定进行有效筛选的算法”。即机器学习的核心是预测。文章介绍如下四种常用的机器学习算法。

2.1 正则化

股票收益预测模型可表示为：

(1)

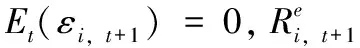
(2)

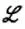
(3)

式(3)的模型被称为弹性网络(Zou and Hastie，2005)。λ和ρ被称为超参数。弹性网络通过ρ的取值包含两个模型。当ρ=1，得到岭回归(Ridge)，它的惩罚项是12范数，岭回归是一种收缩方法，收缩量由超参数λ控制；当ρ=0，得到套索回归(Lasso)，即对模型施加11范数作为惩罚项。套索回归与岭回归的差异是：套索回归不会将系数缩小为0，而是强制其中一些系数为零。套索回归根据λ的取值在预测变量中进行选择，以最大化模型样本外表现，因此它提供了稀疏矩阵解决方案。这两种方法各有利弊，视情况而定。弹性网络回归通过收缩和变量选择，试图规避每一种正则方法的局限性。

2.2 降维

降维方法旨在将高维数据压缩到低维空间，在资产定价问题中，学者们希望在不丢失任何有价值信息的情况下降低因子维度。聚类分析，甚至神经网络也可用来降维(如auto-encoder)，主成分分析(PCA)仍是资产定价中最常用的降维方法。PCA可以用在预测问题和因子模型中。在式(1)的预测回归中，PCA首先将大量的协变量总结为最能描述股票收益小部分变量的线性组合，然后将它们作为解释变量。多因子模型也可以使用PCA：

(4)

(5)

对R进行奇异值分解(SVD)，即对R的样本协方差矩阵进行特征分解：

(6)

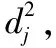
可以通过累积解释的方差比例(PVE)确定K的数量。第K个主成分的解释方差比例是其方差与数据总方差的比例。不断估计主成分，直到它们的累积解释方差比例加起来超过所考虑数据的目标解释方差。这个过程可以指导理论模型中因子数量的选择，当第k个主成分的贡献可以忽略不计时，可以停止提取主成分。由于主成分分析将所有解释变量组合成最能描述数据的线性组合，因此它在高度共线性的情况下尤其有用。

2.3 回归树/随机森林

企业特征之间的交互效应可能对股票的截面收益拥有重要解释力(Freyberger et al.，2020；Kozak，2019)，但传统的回归方法很难将企业特征之间的所有交互项都放入回归模型。回归树是捕捉预测变量相互作用的有力工具。它们还可用于将类似的股票分组，类似于资产组合排序。

树模型是非参数方法，它将特征空间划分为H个区域，称为叶子，每一个叶子包含预测值的估计值。对ri，t+1做深度为L，H个叶子节点的回归树预测：

(7)

Ch(L)是树深为L的区域，θh是一个常数，与叶子节点的平均收益一致。由于每只股票i一定会落入其中一个最终节点，因此其预测收益是该节点的均值。

回归树通过优化预测误差，最小化信息熵对决策树进行分枝。深度为L的回归树可以捕捉最多L-1次的交互，树的规模(深度和叶子节点个数)是控制模型复杂度的参数，一般使用一些调参方法来避免过拟合。一般剪枝方式是先生成H个节点的回归树，然后通过将一些叶子节点合并，将其剪枝成为较小的树，以最小化初始树的最终节点的回归平方和，在剪枝过程中也可以给损失函数添加岭回归和套索回归的惩罚项。

基于回归树的两个重要模型分别是GBDT和随机森林。梯度提升回归树(GBDT)是使用集成方法将目标变量与前一棵树的残差迭代拟合，用递归的方法将浅层树的预测结果结合变成更深的树(Gu et al.，2020)。随机森林是对Bagging的集成方法进行修改，使用相同数量的样本跑回归树，随机森林的预测值是取每个回归树预测值的均值，这种方法旨在减少不同采样中树之间的相关性。

2.4 神经网络/深度学习

神经网络是一种非线性模型，其以高度灵活的方式拟合数据，寻找输入变量与输出变量之间的参数化映射。最简单的神经网络是前馈神经网络，由输入层、隐藏层和输出层构成。在r=g(z；θ)的模型中，输入变量z和输出变量r通过隐藏层估计的未知函数连接，隐藏层相互作用并将输入非线性地转换为输出。隐藏层的层数以及神经元的数目是超参数。

在操作上，训练神经网络包含如下步骤：第一步，根据参数矩阵θ(0)构造输入变量z(0)的线性组合：

(8)

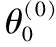
第二步，对第一个隐藏层的每个神经元使用激活函数z(2)=f(z(1))，对于神经网络的选择没有严格限制，最常用的激活函数是Sigmoid或ReLU。隐藏层的输出作为下一个隐藏层的输入，重复进行直到最后输出，返回预测结果。深层的神经网络(隐藏层数量大于2)可以用递归的输出公式表示：

(9)

(10)

也就是说，神经网络的最终输出只不过是非线性函数组合的线性组合。一般使用随机梯度下降的方法估计神经网络的权重。在更复杂的深度神经网络中，常使用反向传播的迭代技术。神经网络因为可以灵活调整神经元数目以及隐藏层深度能够逼近任何函数。神经网络的巨大灵活性是以极易过拟合为代价的，神经网络通过调整学习率、提前停止训练等方法进行正则化。

除了前馈神经网络，还有很多复杂的神经网络结构，例如卷积神经网络、循环神经网络等，被统一称为深度学习模型。循环神经网络专门用于描述具有非线性依赖关系的时间序列数据，其能够从输入变量中提取隐藏状态。并且，可以通过添加长短期记忆单元来捕捉时间序列中未知和潜在的长期自相关。

3 研究设计

3.1 数据选择

文章使用的所有数据均来自东方财富Choice软件整合的公开宏观数据，这些数据定期由国家统计局、中国人民银行、中国外汇交易中心、财政部等相关部门统计公布，根据相关经济背景初步筛选出222个特征，选取了自上证指数存在起始至今的所有交易日数据。文章的被解释变量是上证综指，即将上证综指作为中国股票市场繁荣度指标的代理变量；解释变量是宏观金融数据，选取特征及原因如下。

3.1.1 央行货币政策

股票市场繁荣很大程度原因来自宽松的货币政策，央行货币政策包括“量”“价”调整，“量”是指货币供应量，“价”是指利率。①货币供应量。当央行流动性增加，这些流动性一般呈现出先流向资本市场，再流向实体经济的规律。故货币供应量和股票市场繁荣度呈现正相关关系。选取的有关货币供应量的特征如下：货币供应量M0、M1、M2，分别衡量了处于不同过程中的货币创造；货币乘数；金融机构各部门的货币余额；金融机构新增人民币贷款；货币投放与回笼；银行间同业拆借成交量，等等。②利率。政策利率下降促进贷款利率下降，一方面促使企业家增加借贷投资建厂，促进实体经济投资；另一方面促使投资者进行资本市场投资，促进股市繁荣。选取的有关利率(主要是政策利率)的特征如下：常备借贷便利利率；中期借贷便利利率；实际存款利率、贷款利率；银行间同业拆借加权利率、银行间回购加权利率；准备金率；Shibor。

3.1.2 实体经济指标

当货币政策的传导路径发生阻塞时，央行增发的货币不能直接流入实体经济，而是停留在资本市场。资本市场和实体经济繁荣呈负相关关系。选取特征如下：居民消费价格指数CPI；工业生产者价格指数PPI；社会融资规模；宏观景气指数；消费者信心指数；就业人员平均工资；城镇房地产开发投资；财政赤字；工业增加值，等等。

3.1.3 其他资本市场价格

金融市场具有的投资属性，使得其与其他资本市场繁荣度呈现相关规律，一方面可能出现替代效应：由于黄金、国债、股票属于替代品，其价格可能出现负相关；另一方面可能出现互补效应：由于都是投资品，同时受到货币政策影响，其价格可能出现正相关。选取的其他资本市场价格特征如下：国债到期收益率；证券投资基金成交金额。

3.1.4 进出口

货币政策可能由于净出口和固定汇率制导致央行被迫冲销外币而出现被动的货币政策宽松，正如中国2008年前出现的情况。由于我国特殊的资本管制以及固定汇率制，净出口也可能对金融市场产生影响。选取的进出口特征如下：进出口金额；贸易顺差，等等。

3.2 模型选择

文章采用线性模型和非线性模型对数据进行拟合。如前所述，文章选取特征数较多，故使用带正则项的线性模型；由于假设特征之间存在因果关系，变量之间的关系是非线性的，故采用非线性模型，如树模型和神经网络。

3.2.1 线性模型

由于模型的特征较多，线性回归无法很好地进行拟合，故文章选择了岭回归、套索回归、弹性网络回归以及贝叶斯岭回归四种带正则项的模型。套索回归的损失函数是在最小二乘法的损失函数后面添加了L1正则，即L1范数；岭回归的损失函数是在最小二乘法的损失函数后面添加了L2正则项；弹性网络回归的损失函数是同时添加了L1和L2正则项；贝叶斯岭回归是在参数估计上引入了高斯先验。

3.2.2 非线性模型

文章使用了支持向量机SVM、KNN、决策树、随机森林、XGBoost、神经网络等典型的非线性模型。树模型和神经网络是复杂度比较高的机器学习模型，文章一方面期望使用这些模型以得到更高的拟合效果，另一方面希望通过随机森林和XGBoost的拟合得到对模型贡献最大的特征。

3.3 特征工程及数据预处理

3.3.1 数据清洗

对于缺失值，当缺失值小于50%使用临近值填补的方式，对大于50%的缺失值直接删除；文章不对异常值特殊处理。宏观数据的公布频率不同，有日度数据、月度数据以及季度数据。由于模型标签(上证指数)是日度数据，故需对其他公布频率的数据进行填充，具体的填充方法是用前一月/季的数据对当月/季的数据进行填充，这么填充的原因是：确保预测当天被解释变量的时候所有的解释变量都能获取到。对于缺失值大于该特征总样本量50%的特征，填充难度较大，直接删除。文章不对异常值进行特殊处理。由于所有数据均来自相关统计部门，数据本身的误差属于系统性误差，不影响模型拟合结果，故不对模型数据认定的异常值特殊处理。

3.3.2 特征工程

文章采用归一化的特征处理方式。由于特征的量纲差异过大，譬如：利率的单位是百分数，产值的单位是亿元，在拟合过程中会带来较大误差，通过归一化减轻建模过程中因量纲不同产生的误差。

3.3.3 定义训练集和测试集

模型的解释变量是经过特征工程之后剩下的152个特征，模型的被解释变量是“上证综指”，并以7∶3的比例定义训练集和测试集。在拟合时将标签向后移动三个月，原因是：①出于预测的目的：在预测当前时点的标签时，所有的特征要确保已得；并且，文章希望能够实现预测未来尽可能长的一段时间的标签。②出于解释的目的：宏观经济变量的改变对于金融市场的影响存在时滞，即当央行逆回购释放流动性或财政部增加政府购买后的一段时间，其政策效果才会传递到金融市场。为了将原因和结果更好地连接起来，故选择将被解释变量向前移动。

4 实证结果与分析

4.1 模型预测表现

由于被解释变量是连续变量，故采用R2对模型表现进行评价。上述所有模型的预测绩效汇总如图1所示。结果符合假设，即非线性模型的拟合效果优于线性模型，但有过拟合的倾向，泛化能力较差。文章使用拟合度较好随机森林对未来三个月上证指数进行预测，结果如图2所示。

4.2 变量重要度排序

文章使用XGBoost找出了对模型表现贡献最大的变量，结果如图3所示。重要性变量主要包含货币供应量、就业水平、其他资本市场价格等。变量重要性排名对中国股市的预测性给出了新的解释，货币供应量和其他资本市场价格都符合经济学原理，宽松货币政策对股市带来正效应，其他资本市场也受宽松货币政策的影响，可以侧面反映股市繁荣度，就业人员工资反映了实体经济表现。图4变量边际效应图说明重要性排名前15个变量对模型预测表现贡献已达98%。

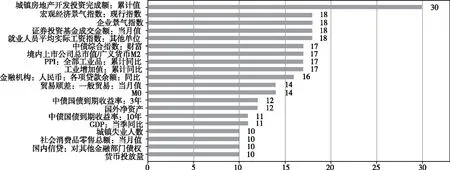
图3 模型表现贡献最大变量

图4 变量边际效应

4.3 预测变量的非线性作用

文章通过刻画就业人员工资与上证指数的关系以及其他资本市场指标与上证指数的关系探究预测变量与被预测变量之间的关系(见图5)。根据就业人员工资与上证指数的折线图，两者没有线性关系，前文所假设的宏观数据对中国股市繁荣度的影响是非线性的假设成立(见图6)。此外，其他资本市场的指标对股市繁荣虽然有促进作用，但在不同区间，其影响程度不同。

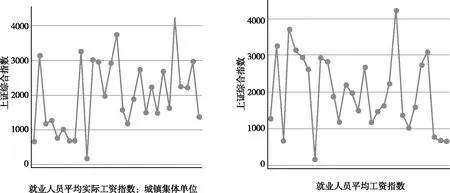
图5 预测变量与被预测变量之间关系

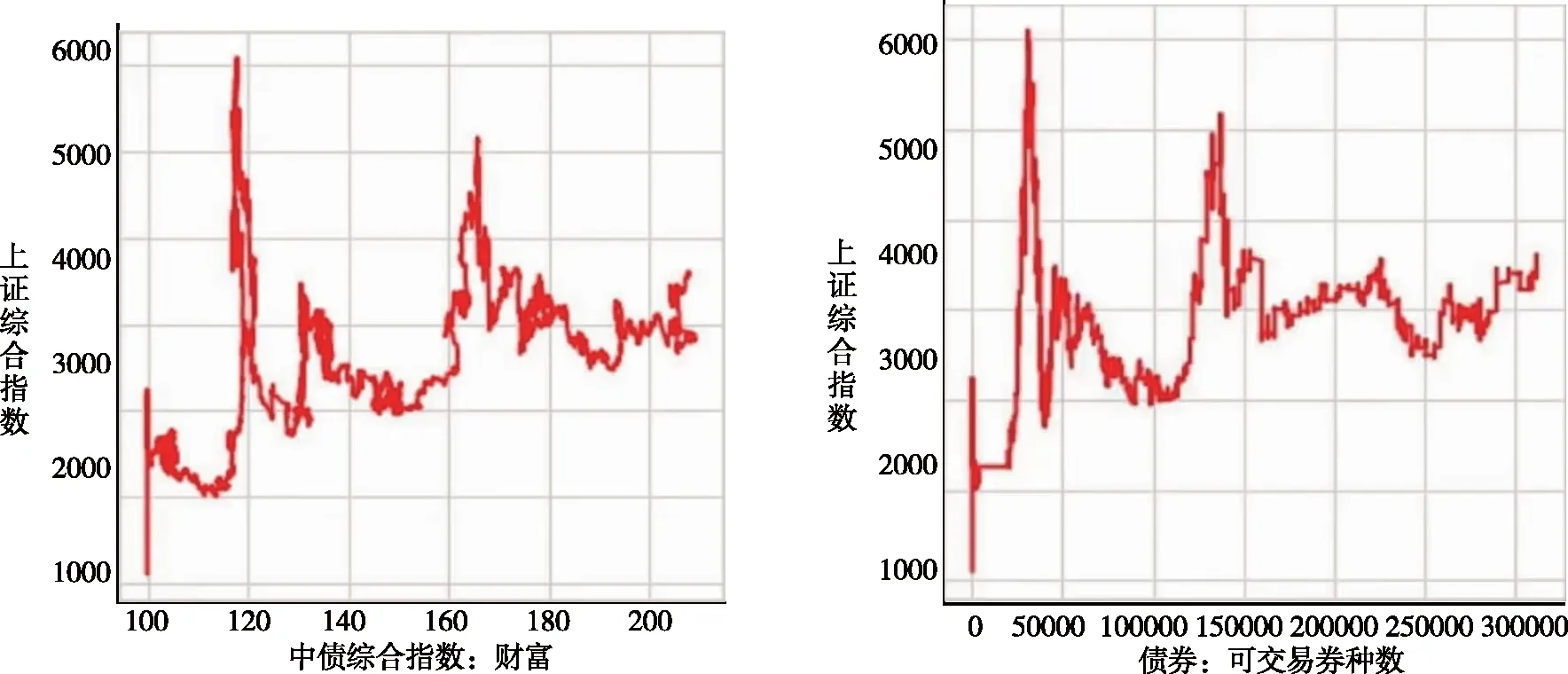
图6 上证指数折线

5 结论

现有的股票预测大多是基于微观数据，对个股价格进行预测。文章基于经济学原理，使用央行政策、实体经济指标、其他资本市场价格指数、进出口等宏观数据特征，以及多种机器学习模型对宏观金融，即股票市场繁荣度指数进行预测。实证结果表明：①股票市场繁荣度是可预测的；②非线性模型的预测表现优于线性模型；③货币供应量、就业水平、资本市场的其他资产价格是对模型贡献度最大的几类变量，这几类变量对中国股市繁荣度指数的影响是非线性的。模型研究样本量过小，在降维方式、变量加工及文本处理上有待进一步完善。