基于ARIMA模型的全球气表温度预测分析

吴会会 王嘉鹏 吴文静 赵宏程 章培军

摘  要：现如今，由于人们在日常的生产以及生活中对化石燃料越来越依赖，温室气体的排放量逐年增多，以致全球变暖的速度也越来越快。为了减少气候变化对人们产生的影响，文章对1918—2022年的全球气温数据进行了平稳化检验和白噪声检验，建立了一个ARMA（1，3）模型，并利用该模型预测了未来5年全球气表温度改变量，结合实验结果，分析了气候改变给人们带来的影响，最后给予了应对全球气候变暖的建议。

关键词：ARIMA模型；气表温度；预测

中图分类号：TP399   文献标识码：A   文章编号：2096-4706（2023）16-0147-04

Global Air Surface Temperature Prediction Analysis Based on ARIMA Model

WU Huihui， WANG Jiapeng， WU Wenjing， ZHAO Hongcheng， ZHANG Peijun

（School of Computer Science， Xijing University， Xi'an  710123， China）

Abstract： Nowadays， due to people's daily production and life more and more dependence on fossil fuels， greenhouse gas emissions are increasing year by year， so that the speed of global warming is getting faster and faster. In order to reduce the impact of climate change on people， this paper conducts a stabilization test and white noise test on the global temperature data in the five years from 1918 to 2022， establishes an ARMA （1，3） model， and uses the model to predict the global air surface temperature change in the next 5 years. Combined with experimental results， this paper analyzes the impact of climate change on people， and gives suggestions to deal with global warming finally.

Keywords： ARIMA model; air surface temperature; prediction

0  引  言

全球气候变暖[1]是一种与自然有关的现象。人们燃烧化石燃料或者树木，产生了大量的二氧化碳，当温室效应不断累积，从而导致温度上升，造成了全球气候变暖。全球变暖不仅会危害自然生态系统的一个平衡，还会威胁人类的生存。根据2021年世界气象组织灾害统计报告，在过去50年里（1970—2019年），几乎平均每天都发生一场与天气、气候或水有关的灾害，这些灾害导致每天有115人失去生命，造成2.02亿美元的损失。在这50年里，有记录的灾害数量增加了5倍，这是由人类引起的气候变化、更多的极端天气事件等因素共同作用的结果。后疫情时代下，气候变化应所需的缺口很大，表明未来全球环境风险和国际合作需求极为迫切。

时间序列预测法[2]其实是一种回歸预测方法，属于定量预测，这方法虽然简便，能迅速求出预测值，但由于没有考虑整个社会经济发展的新动向和其他因素的影响，所以准确性较差。而ARIMA[3]模型是一个时间序列分析方法，该模型被广泛应用于时间序列数据的预测和建模。它可以通过对时间序列的历史数据进行分析和拟合[4]，来预测未来的趋势和变化。其基本思想是，通过对时间序列数据的自回归、移动平均和差分等变换[5]，来建立一个能够描述数据特征的模型，并利用这个模型来预测未来的数据变化。ARIMA模型能够较好地处理许多时间序列数据的特性，如季节性[6]、趋势性、周期性等，并可以用较少的参数来拟合数据。因此，ARIMA模型在经济学、金融、气象学、工业生产等领域中得到了广泛的应用。由于ARIMA模型简单，只需要内生变量而不需要借助其他外生变量，所以本文主要研究了基于ARIMA模型[7]对未来5年全球气表温度的改变量进行预测分析。

1  ARIMA模型

ARIMA（p，d，q）模型的结构如下：

其中，；

表示平稳可逆ARMA（p，q）模型的自回归系数多项式， 表示平稳可逆ARMA（p，q）模型的移动平滑系数多项式。

该模型具有以下优点：1）不需要借助事物发展的因果关系去分析这个事物过去的和未来的联系；2）具有很少的信息量，对趋势性、随机性和相关性的数据都能有很好的预测结果；3）该模型的结构比较简单，预测原理也很容易理解，只需要内生变量而不需要借助一些其他类型的外生变量。基于此，本文利用了ARMA模型预测了未来5年全球气表温度改变量，并结合研究的实验结果，分析了气候改变给人们带来的影响。

2  全球气表温度的预测

本文所使用的数据来源于国家统计局（https：//data.stats.gov.cn/index.htm）官方网站，选取了1918—2022年全球气表温度改变值序列。

2.1  平稳化检验

为了确定没有随机趋势或确定趋势，否则将会产生“伪回归”问题，即有时数据的高度相关仅仅是因为二者同时随时间有向上或向下的变动趋势，并没有真正联系。这样数据中的趋势项，季节项等无法消除，从而在残差分析中无法准确进行分析，所以本文首先检验了全球气表温度改变值序列的平稳性，结果如表1所示。

从表1可以看出，原始序列在滞后阶数为1，2，3的情况下，P值均小于0.05，因此，原始序列是平稳的。

2.2  白噪声检验

为了验证时间序列中有用的信息已经被提取完毕，剩下的全是随机扰动，是无法预测和使用的，即确定原始序列中是否存在相关关系，下面对序列进行白噪声检验，检验所得结果如表2所示。

从表2可以看出，在滞后阶数为6和12时，检验统计量的P值分别为0.007 8和0.009 8，均小于0.05，说明原始序列为非白噪声序列，即序列之间存在相关关系是可以提取的。

白噪声检验的MATLAB代码如下所示：

[h，pValue，stat]=lbqtest（y，'Lags'，[6，12]）

autocorr（y）

parcorr（y）

LOGL = zeros（4，4）;

PQ = zeros（4，4）;

for p = 1：4

for q = 1：4

Mdl = arima（p，0，q）;

[EstMdl，～，logL] = estimate（Mdl，y，'Display'，'off'）;

LOGL（p，q） = logL;

PQ（p，q） = p + q;

end

end

LOGL = reshape（LOGL，16，1）;

PQ = reshape（PQ，16，1）;

[～，bic] = aicbic（LOGL，PQ+1，100）;

reshape（bic，4，4）

p=1;

q=3;

2.3  建立模型

为了选择合适的模型拟合原始序列，下面给出原始序列的自相关图与偏自相关图，结果如图1所示。

图1（a）为原始序列的自相关图，图1（b）为原始序列的偏自相关图，两者均无明显的截尾性，即认为该序列自相关系数与偏自相关系数均具有拖尾性，根据平稳时间序列模型的性质，可选用ARMA（p，q）模型拟合原始序列，根据BIC准则确定模型阶数，结果如表3所示。

根据BIC准则，即在不完全的状态下，对某一部分未知的状态通过利用主观的概率进行估计，然后利用贝叶斯公式对所发生的概率进行一定的修正，最后再利用所得到的期望值与修正的概率进而做出最优的一个决策，其中BIC取值最小的模型即为最优的模型，从表3中可以看出，最小BIC值为-126.460 9，其对应的模型参数的阶数为p = 1，q = 3，因此，本文选择ARMA（1，3）模型来拟合原始序列，拟合结果如表4所示。

从表4可以看出，可知各参数估计值的绝对值均大于其2倍标准差，故每一个未知的参数显著非零，此时的模型是最精简的；如果某个参数不是非常的显著，那么就表示这个参数相对应的这个自变量对因变量的影响不明显，那么该自变量可以从拟合模型中进行剔除，最终的模型将由一系列参数显著非零的自变量表示。因此本文所拟合的模型为：

Var （εt） = 0.014 1

本文所建立模型的MATLAB代码如下所示：

arma=arima（p，0，q）;

fit=estimate（arma，y）

[res，～，～]=infer（fit，y）;

[h，pValue，stat]=lbqtest（res，'Lags'，[6，12]）

T=2020;

t=5;

[yf，yMSE] = forecast（fit，t，'Y0'，y）;

upper = yf + 1.96*sqrt（yMSE）;

lower = yf - 1.96*sqrt（yMSE）;

[yf，lower，upper]

2.4  模型檢验

为了验证本文拟合模型的有效性，验证残差序列{εt}是否为白噪声序列，结果如表5所示。

从表5可以看出，滞后6阶与12阶的P值均显示残差序列为白噪声序列，即{εt}中不存在相关信息，说明模型效果拟合良好，即可以使用该模型进行预测。

因此，得到全球气表温度改变值序列的ARMA

（1，3）模型为：

2.5  全球气表温度的预测与分析

使用该模型预测未来5年全球气表温度改变值及其95%预测区间如表6所示。

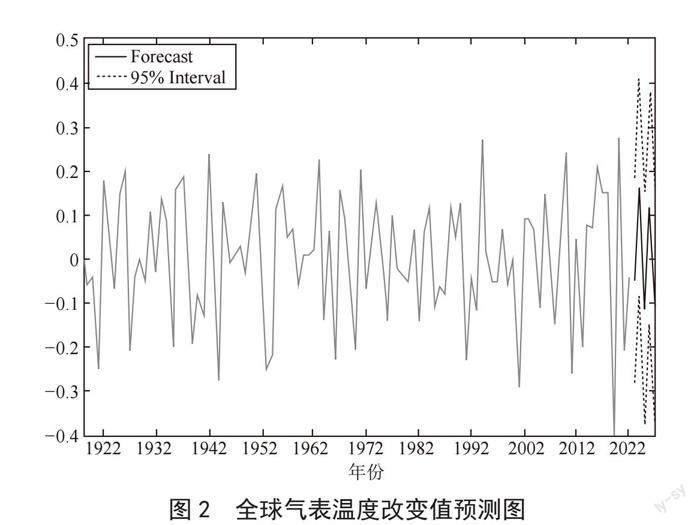
预测图如图2所示，其中，灰色实线代表1918—2022年全球气表温度改变值序列的历史观测值，黑色实线表示该序列未来5年的预测值，两条虚线分别表示预测值的95%预测区间。

从图2可以看出，未来5年的全球气温改变不大，波动在0.1左右。

预测图绘制的MATLAB代码如下：

figure

plot（i，y）

hold on

h = plot（T+1：T+t，yf，'r'，'LineWidth'，2）;

h1 = plot（T+1：T+t，upper，'k--'，'LineWidth'，1.5）;

h2 = plot（T+1：T+t，lower，'k--'，'LineWidth'，1.5）

xlim（[1916，T+t]）

title（'Forecast and 95% Forecast Interval'）

legend（[h，h1]，'Forecast'，'95% Interval'，'Location'，'NorthWest'）

hold off

3  結  论

全球气候变暖是由许多复杂的因素造成的，我们每个人都需要保护好我们的家园。通过对1918—2022年全球气候的改变量作为样本，本文基于ARIMA模型预测出了2023—2027年全球气候的改变量，由实验结果可知，近5年的全球气候改变量不大，但我们仍需保护好我们的家园。

参考文献：

[1] 赵宗慈，罗勇，黄建斌.地球能量失衡与全球变暖 [J].气候变化研究进展，2022，18（1）：119-121.

[2] 王昱，杨修群，孙旭光，等.一种基于全球动力模式和SMART原理结合的统计降尺度区域季节气候预测方法 [J].气象科学，2021，41（5）：569-583.

[3] 李安，高萌萌，陈曦，等.基于MaxEnt模型和未来气候条件预测太行花属植物的适生分布区 [J].河南农业科学，2021，50（4）：137-146.

[4] 陈禹光，乐新贵，陈宇涵，等.基于MaxEnt模型预测气候变化下杉木在中国的潜在地理分布 [J].应用生态学报，2022，33（5）：1207-1214.

[5] 吕彤，郭倩，丁永霞，等.基于MaxEnt模型预测未来气候变化情景下中国区域水稻潜在适生区的变化 [J].中国农业气象，2022，43（4）：262-275.

[6] 智协飞，彭婷，李刚，等.多模式集成的概率天气预报和气候预测研究进展 [J].大气科学学报，2014，37（2）：248-256.

[7] 李荞每，成丽波.基于小波分析的时间序列ARIMA模型预测方法 [J].沈阳师范大学学报：自然科学版，2021，39（1）：49-53.

作者简介：吴会会（1994—），女，汉族，河南信阳人，助教，硕士研究生，研究方向：数据融合。