基于Xgamma分布恒加试验的统计分析
张 锋,戴林送
(安庆师范大学 数理学院,安徽 安庆 246133)
0 引言
寿命试验[1~3]是研究、分析和评价产品可靠性的重要方法。随着时代的不断进步,一些产品的使用寿命得到极大提高,时至今日,市场上高寿命的产品与日俱增,对产品寿命的验证如果采用一般的试验方法耗费时间会进一步增加,故而大多采用加速寿命试验的方法。本文探讨的是加速寿命试验中的一种模型,恒定应力加速寿命试验亦称恒加试验。同时出于对成本和时间的考虑,加速寿命试验通常在所有测试元件完全失效之前终止试验,这种方法被称之为截尾试验,其主要有两大类,一类是定时截尾寿命试验,即试验运行到事先既定的时刻时立刻终止试验;另一类是定数截尾寿命试验,也是本文所探究的对象,将试验运行到事先规定好的失效数量就终止试验,这就使截尾试验在成本损耗上相比于完全失效下的寿命试验有较为明显的优势。
Xgamma分布[4]于2016年被Subhradev Sen 等人发现并提出,该分布为指数分布和伽马分布的特殊有限混合,通过对各种数学性质、结构和生存特性的推导,发现在多数情况下,该分布比指数分布具有更大的灵活性,通过对临床患者的真实数据研究分析发现,相比于指数模型,Xgamma模型更能拟合数据,在医疗等方面更具有普适性。吴清太[5]对Weibull分布在恒加试验定数截尾条件下的情况进行了讨论,利用Gauss-Markov定理对加速方程下未知系数的值进行估计,并对估计结果进行了模拟试验,但基于运用Gauss-Markov定理的门槛较高,很多情形下需要采用其他方法。2021年,Elshahhat Ahmed等人[6]对Xgamma分布的性质进行了研究,使用Lindley近似和Metropolis-Hastings算法对存在自适应Ⅱ型渐进混合删失数据的情况下分布中的未知参数和一些生存特征进行了估计。文献[7]也进一步对Xgamma分布的可靠性特征于三种损失函数下进行贝叶斯估计,模拟的结果表明贝叶斯方法优于经典估计方法。但是,目前有关Xgamma分布的研究大多只是单独从分布的性质和可靠性角度进行分析,未曾考虑该分布在结合加速寿命试验时的情况。
为此,本文考虑在恒定应力加速寿命试验时,定数截尾样本下,Xgamma模型的统计分析。整体从五个方面进行:1)给出Xgamma分布在恒加试验定数截尾情况下的基本假定和实施过程;2)从极大似然估计和Bayes估计两个角度讨论定数截尾条件下Xgamma分布的未知参数值;3)鉴于Bayes估计中存在复杂积分,采用了Lindley近似以及马尔可夫链蒙特卡洛(MCMC)方法获取未知参数的近似Bayes估计;4)通过MATLAB软件对理论推导的未知参数估计进行数值模拟试验;5)对第四步模拟估计的结果进行准确度分析。
1 基本假定与实施过程
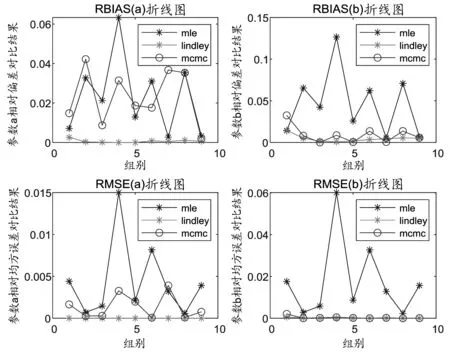
假设1 假设在正常应力S0和加速应力水平S1 其分布函数为 其中θi大于0,i=0,1,…,k. 假设2[8~11]元件的平均寿命θi与试验中的应力水平S之间服从以下加速方程,即 lnθi=a+bφ(S),i=0,1,…,k (3) 其中a,b为参数,φ(S)是应力S的函数. 在元件寿命服从Xgamma分布情况下,定数截尾下恒加试验的实施过程如下: 1)在正常应力S0和k个加速应力水平S1,S2,…,Sk下,加速应力水平之间满足:S1 2)根据科学抽样原理,从一批元件中随机抽中n=(n1+n2+…+nk)个元件进入恒加试验,在应力水平Si下放置ni个元件进行定数截尾试验,试验安排:1)当有第1个元件失效时,记录时刻,并且将剩下的(ni-1)个未失效的元件接续进行试验;2)当发现第2个元件失效时,记录时刻,将剩下的(ni-2)个未失效的元件接续进入下一步试验;3)不断重复下去,直至第ri个测试元件失效时终止试验,并将剩下的(ni-ri)个元件移离试验。假定在应力水平Si下ri个失效,则样本数据遵从 Xi∶1≤Xi∶2≤…≤Xi∶ri,i=1,2,…,k 对于截尾试验,应力Si下的似然函数Li为 可得在k个应力下的似然函数L为 (4) l(θi)=lnL(θi) (5) 将加速方程lnθi=a+bφ(S)代入(5)式,整理可得到含参数a,b的对数似然函数式,为了获取参数的极大似然估计(MLE),对其分别关于a,b求一阶导: (6) 可推得(6)式中的各项为 (7) 在对未知参数(a,b)进行贝叶斯统计分析之前,需要先选取未知参数的先验分布,未知参数的先验分布如何进行选取对整个估计有着举足轻重的作用。 本文采取的是由未知参数(a,b)已有的相关信息获取先验分布,由于此时未知参数a,b皆大于0,因而选取Gamma分布作为未知参数的先验信息分布,并假定两个参数之间相互独立,所以不妨假定本文中的未知参数a,b服从参数为(g,d)的Gamma分布,那么a,b的先验密度为 (8) 根据贝叶斯定理,由先验分布式和似然函数式推得后验分布π(a,b|T)的表达式 取平方误差损失函数,推出未知参数的Bayes估计,对参数(a,b)取g(a,b)=a与g(a,b)=b,得出后验期望[8]为 令eQ(a,b)=π(a,b)p(T|a,b),则有 (9) Q(a,b)=l(a,b)+ρ(a,b),l(a,b)=lnp(T|a,b),ρ(a,b)=lnπ(a,b) 由此可推得Lindley近似和MCMC算法. Lindley[10]于1980年提出了一种解决近似贝叶斯估计中出现积分的方法。使用该方法可获得各种寿命模型参数的贝叶斯估计量。贝叶斯分析中的积分比率由下式得出。 (10) 其中Θ={θ1,θ2,…,θm},u(Θ)是关于Θ的函数,lnL(Θ)是对数似然函数,ρ(Θ)取先验信息的对数,对于大样本和某些正则条件,式(10)可以通过以下展开式近似 在本文中,由于m=1,因此式(11)可变化为 对参数a的Lindley估计 其中 对ρ(a,b)中的参数a求偏导,得到 同理可对参数b的Lindley估计: 其中: 此时将b′,b″,Lbbb,ρb,wbb一同代入E(b|T),即可以求出E(b|T). 在Bayes算法中,还有一种对后验期望E(a|T)进行估计的经典算法,即对未知参数采用蒙特卡洛马尔科夫链的方法进行计算。由于文中后验期望E(a|T)是复杂积分无法直接抽样,因此这里用到了MCMC方法[11]的MH抽样法。 令目标分布的概率密度函数为g(a),则有 从q分布中产生一个随机数a*,有 故接受概率为 若 则a1=a*,否则令a1=a0,一直下去产生一组随机样本序列a0,a1,a2,a3,…,ai. 由此可得基于恒加试验下Xgamma分布定数截尾条件下的两种参数估计,现利用MATLAB软件对估计进行有效性分析和精度评估。 具体步骤如下: 1)本文首先根据对a,b两个未知参数各自的取值范围设定初始值,这里取θ=4,a=0.49,b=0.38. 2)从Xgamma分布中生成n个随机观测值,本文分别取样本容量为20、40、60、80、100、120、140、160、180和200,依据定数截尾恒加试验的试验原则,取在2个应力加速水平fi=2∶3下的两组样本情况进行试验模拟,并且分别选取不同数量的截尾数,得到在各自情况下的截尾样本。 3)根据获取的截尾样本,对未知参数进行近似估计。在MLE中,将2 000次反复迭代的结果均值作为未知参数a,b的最终估计结果;在Lindley算法中给定初值g1=2,d1=1.5,g2=5,d2=4.1,重复上述步骤并记录结果;对于MCMC算法,本文给定初值g1=5,d1=3.3,g2=5,d2=4.1,对每组参数进行迭代运算2 000次,取链长为30 001,对2 000次迭代运算的第20 001到30 000个数据链求平均值作为迭代运算的结果,结果见表1. 表1 模拟试验结果 4)记录上述步骤结果并计算未知参数的相对偏差和相对均方误差,结果见表2.并对a,b两个参数的RBias结果绘制折线图,使结果的呈现更加形象直观。如图1所示。 图1 数据模拟对比分析 表2 模拟试验结果分析 由试验结果可以看出:比较Lindley、MLE、MCMC三种算法关于Xgamma分布参数的近似估计结果,通过观察表1与表2的试验数据,结合图1中的相对偏差(RBias)与相对均方根误差(RMSE)的折线趋势,在本文的假定模型下Bayes估计的精确程度更好,尤其是Lindley近似推出的Bayes估计结果更加稳定,说明Bayes估计的结果是可靠的。 讨论了当元件寿命服从Xgamma分布时,在定数截尾方案下恒加试验的参数估计。利用最大似然估计和贝叶斯估计方法对未知参数进行了推断,利用Bayes估计能够减少繁杂的积分问题,进而提升参数估计的精确程度。结果表明,使用贝叶斯估计中的Lindley近似和MCMC算法都能较极大似然估计获得更加精确的结果。2 极大似然估计
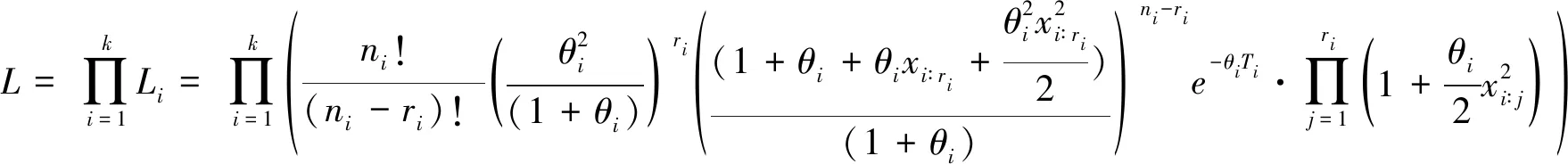
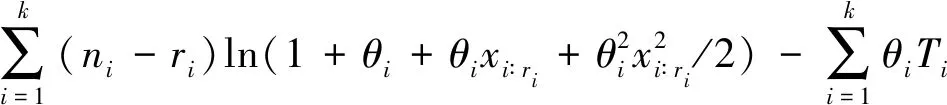




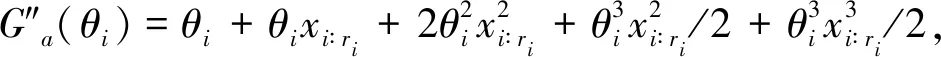
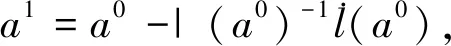
3 贝叶斯估计


3.1 Lindley近似算法

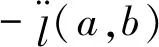
3.2 MCMC算法

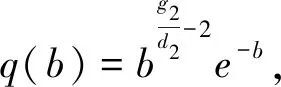
4 数值模拟


5 结束语

