探究式教学在人工智能专业核心课程中的实践研究

何 苗

（宝鸡文理学院 计算机学院，陕西 宝鸡 721013)

1 学情分析

1.1 背景分析

工程最优化设计[1]、模式识别[2]、深度学习与应用[3]、机器学习与应用、计算机组成原理等课程是针对人工智能专业的学生开设，其先行课程为线性代数、高等数学、离散数学、概率论与数理统计等。由于先行课存在课时压缩的问题，加之有些学生对数学的理解能力较弱，使得好多理论和知识点并没有真正理解，只是会做题而已。针对上述问题，因此在讲授专业核心课程时，先对需要的数学基础知识进行讲解。让学生加深理解之前学习过的数学基础知识，进一步需要给学生讲解最优化问题的数学模型，培养和提升学生通过实际过程中学习建立数学模型和算法的设计，将实际问题转化为数学问题，有效解决实际问题。最终达到培养学生思考问题、分析问题和解决问题的能力，进而培养学生的数学思维模式。

1.2 研究现状

工程最优化设计这门课程的教学重点是线性规划方法、无约束最优化方法、约束最优化方法、智能最优化方法和最优化问题的计算机求解。每一种方法讲解的时候同时需要利用计算机进行求解。由于这门课程仅有16节实验课，很难在这么短的时间内完成实践任务，因此由于课时的原因，很难将理论和实践相结合。如果学生认识不到学习这门课程对自己未来的作用，很难有兴趣和积极性，导致这门课程在教学上有一定的阻力。

工程最优化设计这门课程的教学目标使学生能较深刻地理解工程优化设计的基本思想和方法，加强最优化问题的数学基础知识，熟悉优化建模和常用的一维搜索方法，掌握梯度法、牛顿法、变尺度法、共轭梯度法，最小二乘法、单纯形算法、遗传算法、神经网络算法等，并且能运用优化的观点和方法，通过编程解决实践中遇到的工程优化问题，从而提高学生应用专业知识，对具体的实际问题进行合理的分析，并给出可执行的方案，最后借助计算机的工具解决实际问题。

2 探究式教学方法的探索

探究式教学方法探索途径主要有四种方法，如图1 所示。以相关竞赛激发学生的学习兴趣、以任务为结果增强学生学习的积极性、以合作探究作为教学的主要方式和将实际案例的讲解融入专业核心课程中。

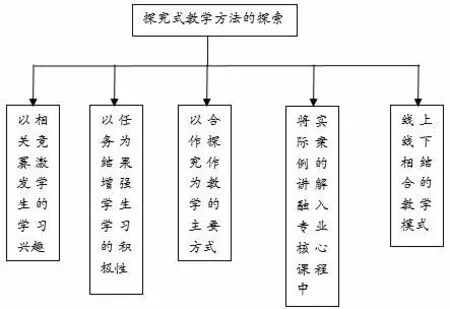
图1 探究式教学方法探索途径

2.1 以相关竞赛激发学生的学习兴趣

计算机学院的学生数学基础知识相对较弱，因此缺乏学习工程优化理论的兴趣，总感觉学好工程优化知识对自身未来的发展帮助较少，因此对这门课程不够重视。为了激发学生的学习兴趣，首先可以给学生介绍相关的大学生比赛和竞赛，比如：中国国际“互联网+”大学生创新创业大赛、全国大学生数学建模竞赛、中国大学生计算机设计大赛、“中国软件杯”大学生软件设计大赛等；其次，给学生讲解学好工程优化理论的知识和方法对参加这些比赛的重要性；最后，告诉大家参加这些大赛对自身发展的重要性。比如全国大学生数学建模竞赛的官网上的宣传语就是：“一次参赛，终身受益”。

2.2 以任务为结果增强学生学习的积极性

为了提高学生学习的自觉性和积极性，根据学生掌握工程最优化的基础知识和方法以及Matlab[4-5]编程能力，设计相应的实践内容和任务。具体操作可以将学生分组，由组长统一协调安排，每组成员可以通过讨论协商，共同完成任务。这样不仅能锻炼学生解决任务的能力，而且还能培养学生的团队协作能力。

2.3 以合作探究作为教学的主要方式

为了有一个很好的教学效果，为了让学生深刻理解所学习的知识，为了学生能将所学习的知识解决实际问题，教师可以尝试以合作探究作为教学的主要方式。首先是教师给学生介绍相关的学习知识点和内容，接下来需要给学生提供学习内容的相关材料，比如课本、课外参考书目、相关的学习视频、MOOC资源等；然后让学生自己学习，学生可以先自学然后分组讨论学习的内容，接着教师需要通过检测来发现学生学习上的漏洞和欠缺，进而补充或者纠正相应的知识点和内容，根据学生学习的情况给学生布置相应的实践任务，学生可以通过分组来完成实践任务，教师根据学生完成任务的情况进行点评，提出任务完成过程中的亮点和不足；最后让学生自己总结完成任务的情况，提出今后改进的具体措施。合作探究的教学方式主要目的是提高教学的效率，提升教学的效果，让学生真正掌握所学习的知识点和内容，最终能分析实际问题、解决实际问题。

2.4 将实际案例的讲解融入专业核心课程中

将人工智能专业核心课程的教学分为课前、课中和课后。课前，教师通过教学分析、教学设计，将教学资源推送给学生，有些基础知识可以通过MOOC资源或者教师录讲课的小视频推送给学生，让学生自己学习，有些知识点需要学生自主预习。课中，教师通过课程导入、新课讲解、求解问题和归纳总结四个步骤完成课堂的教学工作，学生在课堂中需要积极参与进来，需要进行小组讨论，最后归纳总结，课堂反馈。课后，教师需要评估教学，鼓励学生在课后以小组的形式相互设计问题，进行描述模型并且通过所学习的知识点进行实际问题的求解，教师此时只需要负责引导和点评，让学生自己独立地思考问题、分析问题和解决问题。培养和提升学生在实际过程中解决实际问题的能力。让学生的学习由被动变为主动，调动学生的积极性。

在给学生提供实际案例的时候，可以给学生提供一些数学建模比赛的真题。例如2021年全国大学生数学建模比赛C题，是一个基于最优化模型的生产企业原材料订购与运输研究方案。首先给学生提供比赛真题，让学生自己尝试去解决，然后讨论学生解决过程中存在的问题和碰到不能解决的难题，最后详细讲解真题。下面来具体分析一下这道真题。企业在生产产品的时候所用到的原料不同，每种原材料的价位不等，制作相同产品所需的原材料也不相同。面对上百家的供应商，为了不耽误生产，节约成本，应该如何制定一个原材料的订购方案，目标是使得企业的利润达到最大化。如果再考虑运输成本，那么订购方案又该如何选择。还有就是应该如何选择转运商来解决运输材料的问题，不同的转运商面临着距离和价位的不同，还有就是对原材料的消耗也不等，如何制定最佳的转运方案也是这个实际问题需要解决的。首先针对第一问，在众多供应商中如何选择最重要的50家供应商，在解决这个问题的时候，根据实际情况考虑到这家供应商的信誉会对企业产生重大的影响，因此给出容错率的概念，选择容错率较小的企业，然后建立最优化模型，通过运用Matlab软件得出满足最优化模型的最重要50家供应商。下面需要在这50家供应商中选择最少的供应商来满足企业的生产需求。这个问题可以通过根据制作单位产品的时候每种原材料的消耗情况，每种原材料的价位以及在满足企业生产需求的情况下建立最优化模型，然后运用Matlab软件得出满足最优化模型的最少的供应商。当供应商提高自身能力增加供货量、企业每周的产能增加或者转运商降低损耗率，即满足约束的数值会发生变化，则最优解可能会随之发生变化。因此，需要研究当约束数值发生变化时，基于灵敏度分析得出所研究的最优模型的最优解会发生什么样的变化或者变化很小。进一步，通过使用灵敏度分析，需要讨论约束数值在何种范围内变化不会影响最优模型的最优解，即无须改变决策方案。最后还可以通过灵敏度分析方法讨论约束数值发生 变化时，最优方案发生何种变化。

2.5 线上线下相结合的教学模式

基于“互联网+”的大环境，在数字化、智能化和网络化信息下，结合计算机学院的专业特点，将线上教学和线下教学相结合，做到全方位地实现教学模式。在一般的情况下，将线上教学用于线下教学的辅助，有效的帮助学生学习到更多的知识点和对未来工作和科研有帮助的内容。线上教学主要用于课前和课后。在课前，利用微信群、QQ群或者雨课堂发布学生需要预习的内容和需要提前学习的知识点。教师可以给学生录制小视频或者发布MOOC 资源上的学习视频。课后，可以利用微信群、QQ群或者雨课堂给学生布置课后作业，解答学生的疑问，在案例教学的过程中，可以让学生分组来完成一些实际的案例，培养学生团队协作能力和解决实际问题的能力，通过协作完成任务，可以让学生之间相互学习相互帮助，既可以增加同学情谊又能更好的完成任务。提倡学生之间分享任务完成的结果和方法，教师此时只需要做到监督和讲评。

3 优化理论核心课程的实践研究

最优化问题就是用最少的付出获得最大的受益。对于工程设计问题，即寻求设计参数的一组最佳值，使其既满足各种设计标准和要求，又使一项或多项技术经济指标达到极值。首先，对实际问题进行数学描述,建立一组数学表达式，称数学模型，数学模型是对实际问题的数学描述和概括，是进行最优化设计的基础。根据设计问题的具体要求和条件建立完备的数学模型是最优化设计成败的关键；其次，寻找一种数值计算方法和相应的计算机程序；最后，通过撰写代码进行求解。最优化问题的算法的分类如图2所示。根据问题的性质分为线性和非线性；根据问题的特征分为单变量和多变量，有约束和无约束；根据算法的特征分为定点转化、一维搜索、利用导数、不利用导数、直接求解和间接求解，具体的算法有：单纯形法、黄金分割法、二次插值法、梯度法、牛顿法、变尺度法、共轭梯度、鲍威尔法、可行方向法、序列二次规划法、惩罚函数法、乘子法、遗传算法和神经网络算法。

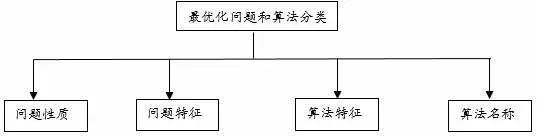
图2 最优化问题和算法的分类

4 推广的价值

通过学习人工智能专业核心课程，使得学生掌握优化理论的方法，培养学生以较高的抽象方式看待优化理论。专业核心课程理论与技能培养并重，通过这些课程的学习，使学生理解优化理论、模式识别、深度学习与应用等课程在人工智能专业中的作用和地位，掌握基本概念、基本原理、核心技术和方法；引导学生了解学科前沿进展，为今后从事与相关领域研究和工作奠定基础，迎合了新世纪的社会发展和现实需求，能从根本上提高学生的专业水平和社会竞争能力，有效推动专业的建设与发展，并有利于促进和提高地方高校工科专业的办学水平和特色。本课题的研究成果，能有力推动我校人工智能专业的进一步发展。给本科课程现阶段存在问题，并给出相关可行的改革方案。

5 小结

针对教学重点和难点， 将探究式教学方法的探索融入人工智能专业核心课程。以相关竞赛激发学生的学习兴趣、以任务为结果增强学生学习的积极性、以合作探究作为教学的主要方式和将实际案例的讲解融入专业核心课程中。以某个实际问题为主线，通过问题的提出、分析和解决三个步骤完成求解。具体通过案例引入问题，启发学生思考，从而化解教学重点和难点。本课题的研究成果，能有力推动我校人工智能专业的进一步发展。给本科课程现阶段存在问题，并给出相关可行的改革方案。