考虑客流时变特性的列车时刻表优化方法

张矢宇, 杨云超, 杨宇昊

(1.武汉理工大学 交通学院,湖北 武汉 430063; 2.河南省交通规划设计研究院股份有限公司,河南 郑州 450000)

0 引言

近年来,城市轨道交通凭借其容量大、速度快、消耗低和绿色环保的特点迅速成为解决大城市拥堵问题的优先考虑对象。客流是交通运输能力和运输系统合理配置、制定运营计划的重要因素。城市轨道交通中的乘客流量明显存在时间和空间不平衡,沿线各车站的入站和出站车站的乘客流量差异很大。目前国内外城市轨道交通的出发间隔一般根据每小时的OD客流量或每小时最大客流量确定,运行方式为均衡运行方式。同等间隔的平衡列车模式易于管理,广泛用于控制国有和城际列车的运行,但对于城市地铁,这种调度模式可在高峰时段使用,队列中的等待时间太长,非高峰容量被浪费,并且每列的载客率不平衡,将不可避免地导致运营成本增加或服务水平下降,阻碍了城市轨道交通服务水平的提高。研究表明利用实际动态客流信息、科学建模方法和优化算法来解决城市轨道交通中的时间表优化问题是十分关键的。

国内外对于轨道交通时间表优化的研究成果较为丰富,研究成果较多。随着动态客流信息可获取性越来越强,使用动态客流信息进行时刻表优化,能为乘客提供更好的旅行服务[1]。曹亮[2]构建了基于客流需求的旅客列车时刻表优化模型;许得杰等[3]构建了考虑客流时变需求的大小交路列车时刻表优化模型;ZHU等[4]构建了考虑乘客出发时间的时刻表优化模型;祁奇[5]构建了基于动态客流的城轨列车时刻表优化模型。对现有单线时间表优化的研究考虑了动态客流特征,主要是通过优化时间表来减少乘客等待时间[6,7],缺乏对更灵活的停车模式的研究。综上所述,对时间表的优化研究不单单要考虑客流的时间不平衡,同时也要考虑其空间不平衡,即考虑客流的时空不平衡性。

基于以上成果,本文分析了城市轨道交通客运需求的时变特征,给出了一种基于客运效率计算客运成本的方法;建立了城市轨道交通列车时刻表的优化模型,并设计了一种基于仿真的两阶段遗传算法求解该模型;以武汉地铁一号线为例进行实证分析,验证了模型和算法的有效性。

1 考虑客流时空特性的列车时刻表优化模型

1.1 问题描述

(1)研究对象

如图1所示,城市轨道线路共有n个站点,列车出发方向记为f=1,返回方向记f=2。所有列车从出发站出发,到终点站后返回,休整后进入等待下一次出发的空闲车道。

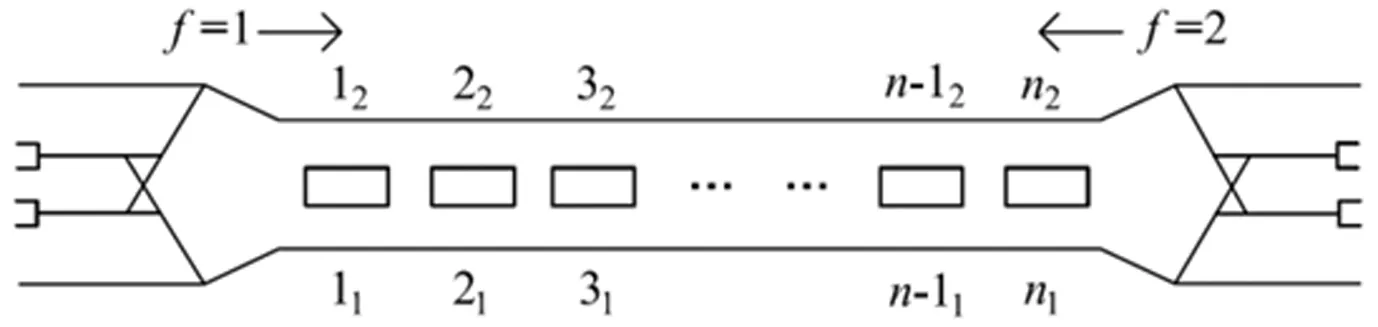
图1 城市轨道交通线路示意图

(2)研究时段

为了更好地解释乘客的乘车过程,将为不同的车站分配不同的研究时段,具体见图2。每个站的研究时段如下:

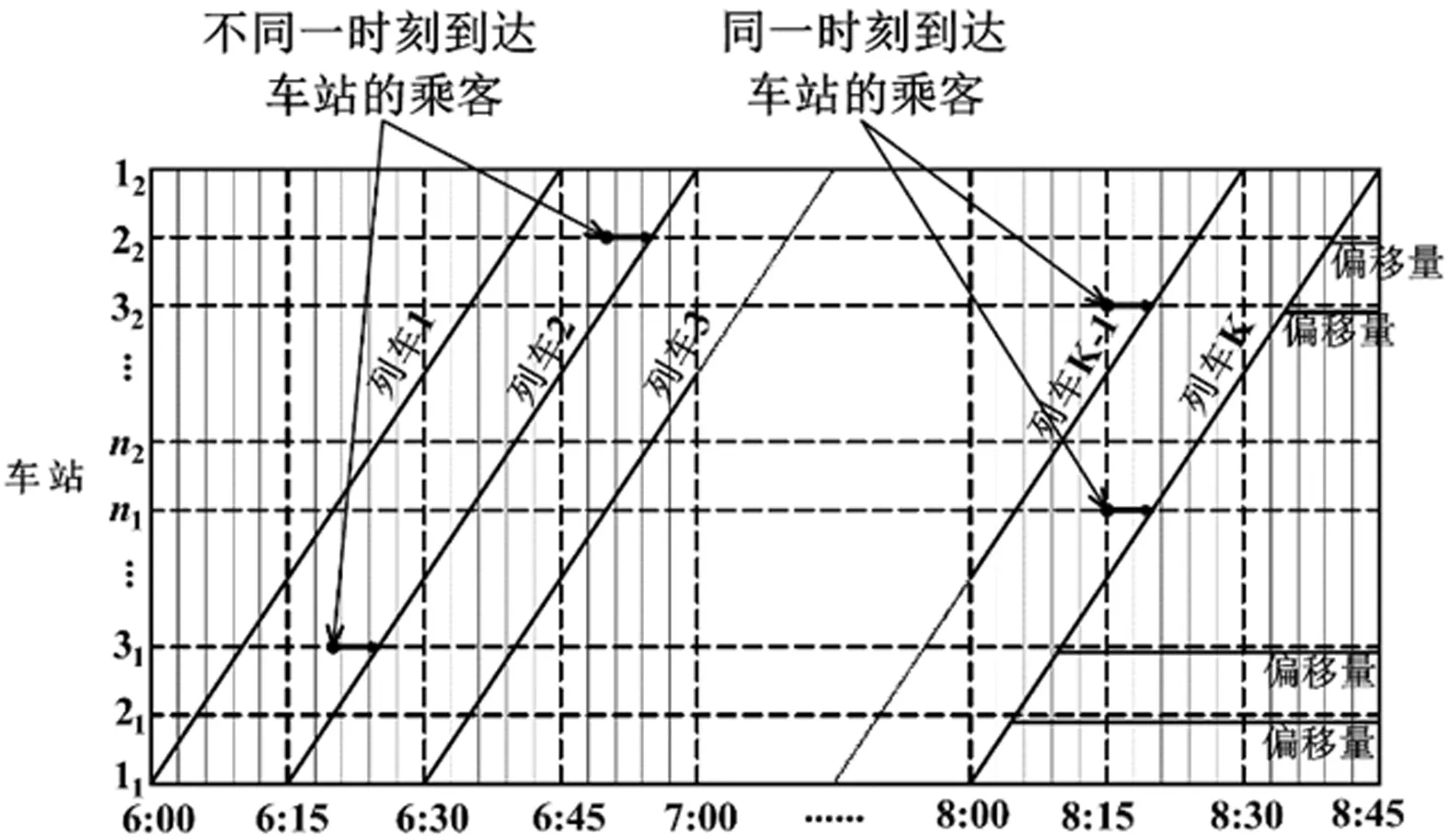
图2 运行图示例

车站11:[Tb(11),Te(11)]=[6:00,8:00]

车站21:[Tb(21),Te(21)]=[6:06,8:06]

……

车站22:[Tb(22),Te(22)]=[6:39,8:39]

车站12:[Tb(12),Te(12)]=[6:45,8:45]

整个研究时段为[0,T],0表示开始时间,即图2中的6∶00,T表示结束时间,即图2中的8∶45。为了便于建模,将[0,T]离散化为一系列相等长度的时间段,[0,T]可以表示为一组离散节点的集合,Γ={0,1δ,2δ,3δ,…,(m-1)δ,mδ}。这里,δ表示时间间隔,0表示研究时段的开始时间,mδ表示研究时段结束时间。为了简化说明,在后面的时间的说明中省略了时间间隔δ,即Γ={0,1,2,3,…,(m-1),m}。

1.2 基本假设及变量定义

(1)基本假设

根据研究经验做出假设,具体如下:

①沿地铁运输路线的车站的旅行需求和乘客到达分布是已知,且相对稳定的。

②所有列车在相同路段的运行过程和时间都是固定且相同的。

③所有列车为同一款列车,容量是已知,且在列车运行期间,不允许乘客数量超过列车上的最大人数。

④车站的设计容量是已知的,并且车站的最大容量不应超过车站的设计容量。

根据研究,在车站聚集的人数与在平台上等待的人数和下车的乘客数量密切相关。由于每列列车的乘客人数众多,预测下车人数较为困难。为简化计算,本文仅预测在研究期间可以沿着线路下车的最大人数,并且将车站容量安全约束转换为在车站等待的人数。可以使用以下公式计算在车站等待的最大人数:

(1)

(2)变量定义

模型中变量具体定义如下:

N:车站,N={1,2,3,…,n};

Nf:车站站台,Nf={11,12,21,22,…,n1,n2};

uf:当f=1时,站u的上行方向上的站台,当f=2时,站u的下行方向上的站台;

L:运行线路的长度;

R:列车编号,R={1,2,3,…,rmax};

r:开行列车编号;

rmax:最大列车编号;

Puν:车站u的乘客前往车站ν的概率;

qu:研究时段到达的乘客总数;

du:列车在车站u停车的时间;

Su,u+1:列车在时间段[u,u+1]的运行时间;

e1:在出发站1修整列车的时间;

en:在n站折回列车的时间;

m:离散时间段长度;

φ1:每单位时间购买列车车厢的成本;

φ2:列车车厢的行驶距离转换费;

η:乘客等待值;

Hmax:最大发车间隔;

Hmin:最小发车间隔;

CT:列车容量;

B:列车数量;

ϑ:最大载客率;

θu:乘客到达阀值,如果在车站等候的乘客数量小于θu·γu,乘客可以进入车站u,否则乘客将等待下一站机会,需要在车站外排队;

ωu,t:0-1变量,如果站u允许乘客在时间t进入车站,则ωu,t=1,否则ωu,t=0;

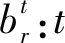
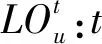
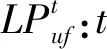
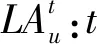
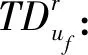
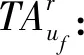
TFr:列车r重新进入空闲车底的时间;

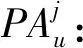
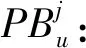
K:可用车辆的总数;

NFt:t时刻站1的具有空闲车底数,NF0=K;

σu,t:0-1变量,当车站u处于拥挤状态时,即当不允许乘客进入车站时,σu,t=1,否则,σu,t=0;

xt:0-1决策变量,如果在时间t有列车离开站1,则xt=1,否则xt=0;

X:决策变量向量,X={xt,t∈Γ}。

1.3 优化模型

(1)目标函数

运行单位总是希望满足乘客的出行需求的条件下尽可能地降低运营成本;乘客总是希望尽可能高效地出行。因此,城市轨道交通业务的决策部门需要从整个系统的角度全面考虑双方的利益,优化列车时刻表。

①运营单位

地铁运输运营成本一直是相关运营单位在优化城市轨道交通列车时刻表方面的重点。本文的运营成本主要包括调查期间购买列车的成本和行驶距离的成本。研究时段的列车购买成本可以通过以下公式计算:

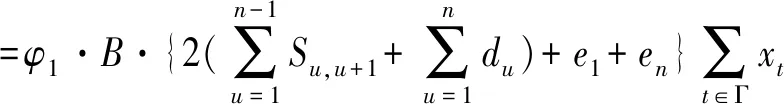
(2)

研究时段列车行驶公里的转换成本可以通过以下公式计算:

(3)

②乘客

作为城市轨道交通的服务,乘客总是希望提高效率。然而,一旦地铁线路和车站完工,将很难改善乘客的步行和乘车时间。因此,本文重点关注减少乘客等待时间,通过减少乘客的等待时间来提高乘客的出行效率。

每个乘客的移动过程简单描述如下:到站-进站-候车-上车-下车-出站。乘客等待过程可分为以下站内等待和站外等待两种。

基于上述分析,乘客上车和到达的时间差就是实际等待时间,具体如下:

(4)

然而,由于等待环境的影响,乘客对车站外的等待时间敏感,而等待列车的等待时间由于列车满载而使得感知的等待时间长于实际等待时间。因此,在本文中,通过引入惩罚系数α和β(α,β>1),此参数表明了乘客站内外等待时间的感知误差。另外此处引入了时间价值因子,将乘客的等待时间转换为乘客的广义等待时间成本。乘客的总等待时间如下:

(5)

(2)列车时刻表优化模型

基于以上分析,建立如下的优化模型:

(6)

(14)

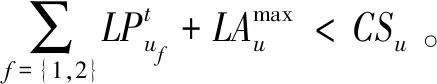
2 基于仿真的优化模型求解方法

遗传算法是模拟生物进化机制的全局随机搜索和优化算法,被广泛用于解决运输行业优化问题[8-11]。基于以上分析,提出了一种基于仿真的遗传算法求解该模型。

2.1 仿真过程

列车仿真过程模拟包括列车出发和列车到达两个事件。具体仿真模拟过程如下:

①当根据列车的时间表确定每个列车出发站的出发时间并且将模拟时间提前到列车的出发时间时,即是否满足列车的出发需求。如果空闲车底存在(NFt≥1),列车将准时离开出发站,相反,如果没有空车的底部(NFt<1),列车将按计划出发。

②当列车开始运行时,根据行程和停止时间,按顺序计算列车沿车站的到达和离开时间。

③当列车返回出发站并且修理工作的时间结束时,列车使用的车底进入空闲车底行列,此时,NFt←NF+1。

另外,列车下车最大人数直接影响每个车站最大乘客人数的计算结果、乘客的等候时间和每列车的乘客人数。然而,由于在模拟之前难以准确地计算来自每个站的列车的最大数量,因此在本文中,在模拟期间添加反馈处理,并且不断更新每个站的最大列车数量,确保其小于车站的安全容量。

2.2 基于仿真的两阶段遗传算法

由于决策变量X是与二进制编码形式相似的0-1变量,直接将其作为遗传算法的染色体。

根据解向量X的结构,可以看出,可以表示任何一种开行方案,即在研究时段从始发站发送的列车的数量可以从0～m变化。然而,如果两列地铁列车之间的距离太长或太短,由于约束(7)和(8)难以满足,大多数开行方案将不可行。如果仍然使用传统的遗传算法求解方法,则需要大量的计算时间来随机生成具有特定可行性的指定数量的初始解决方案组。为提高效率,提出了一种基于仿真的两步遗传算法。具体过程如下:

(1)阶段1:产生初始解候选集合

为提高效率,在优化之前提前部分生成初始解候选合集。

①生成均衡方案合集。该方案为等间隔发车,解决方案相对简单,枚举法即可以快速找到部分可行解。故采用枚举法,将每个均衡运行计划依次输入到仿真模型中,选择所有可行的均衡运行计划。

②丰富最初解决方案。基于均衡方案生成的初始备选解决方案,通过变异操作生成部分不平衡方案,将方案代入模型,若结果可行,将方案加入候选初始解,否则则舍弃该方案。此过程中具体变异过程如下:从初始候选组中随机选择亲本染色体,随机产生实数a∈[0,1],如果a≤0.5,则使用突变规则I突变父染色体(见图3)。否则,使用变体染色体II突变亲本染色体(见图4)。

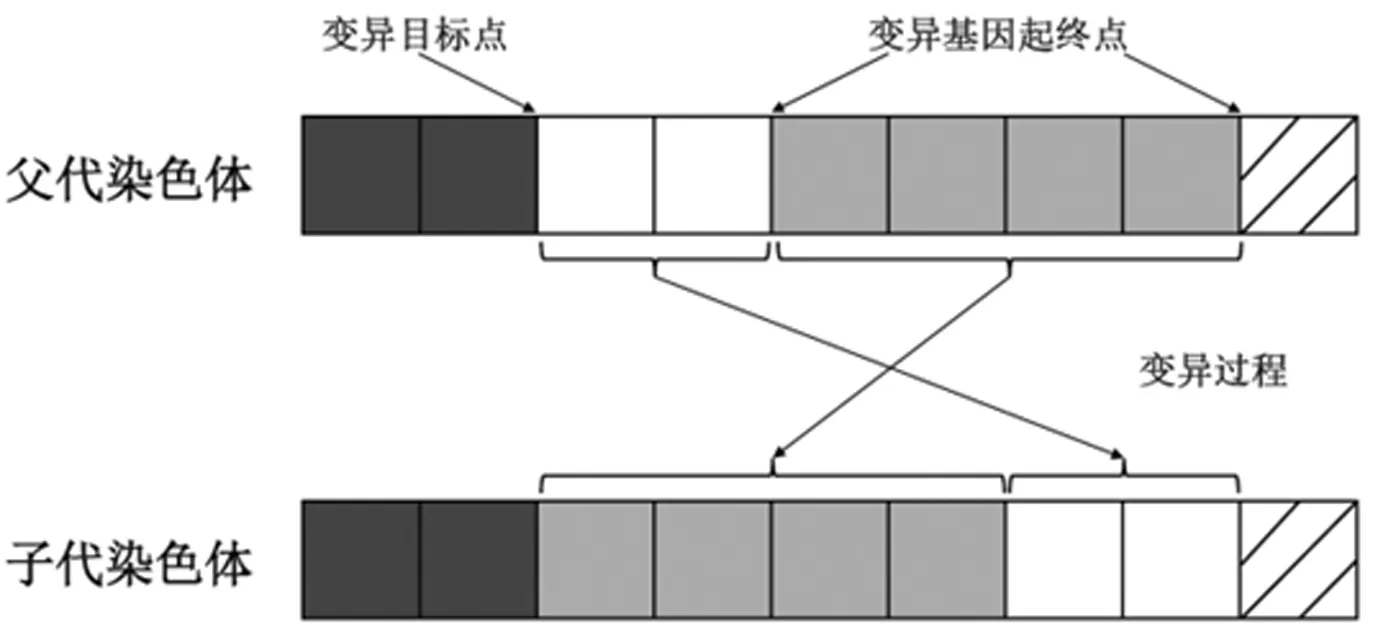
图3 变异规则I:基因片段内部重组

图4 突变规则II:单点变异

(2)阶段2:遗传算法优化

该优化过程包括6个步骤:

步骤1生成种群进化代数最大值max_generation。

步骤2从之前生成的方案中随机选择pop_size个染色体作为初始种群。

步骤3将每条染色体的驱动方法输入模型中,运行获得参数值,并代入自适应函数以获得每条染色体的自适应函数值。在本文中,选择目标函数(6)作为遗传算法的适应度函数:

Eval(Xk)=z(X),∀k=1,2,…,pop_size

(15)

在该等式中,Eval(Xk)表示对应于染色体Xk的适应度函数值。

步骤4使用轮盘赌方法,从亲代染色体群体中选择pop_size个染色体以形成子染色体群体。具体程序如下:

步骤4.1找出最大的适应度函数值F:

F=max(Eval(Xk))

(16)

步骤4.2令P0=0,计算累积选择概率Pk:

(17)

步骤4.3随机生成实数a∈(0,1],并将其与累积选择概率Pk(k=1,2,…,pop_size)进行比较以选择第k个染色体(Pk-1

步骤4.4结束条件判断。如果选择pop_size个染色体,则终止选择操作并输出子染色体群,否则过程进入步骤4.3。

步骤5两个选择的亲本染色体交叉操作产生新的染色体。具体程序为:

确定染色体交叉概率Pc,随机选择两条染色体,同时随机生成实数a∈[0,1],如果a≤Pc,则遵循单点交叉规则(图5)染色体相交。

图5 交叉规则:单点交叉

步骤6随机选择染色体突变,程序如下:

步骤6.1确定染色体交叉概率Pc,随机选择染色体,同时随机生成随机数a∈[0,1],如果a≤Pc,则进行步骤6.2以突变染色体;否则,父代染色体不改变。

步骤6.2随机生成实数b∈[0,1],如果b≤0.5,改变父染色体,此时改变规则遵循突变规则I;否则遵循突变规则II。

步骤6.3将新生成的染色体代入模型进行模拟验证,若方案可行,则将新染色体加入到子染色体群。

步骤7当算法达到最大进化代数时,算法结束并输出最佳染色体;否则进化代数增加1,进入步骤3。

3 武汉地铁一号线时刻表优化分析

3.1 参数设置

武汉地铁1号线由26个站组成,站间的行程时间设置为5分钟,每个站点的停止时间为30秒,返回站点的周转时间和出发站点的翻新时间均为90秒。每个站台的设计容量为2000,安全阈值θu=0.65。优化目标是在出发站1处制定每列地铁列车的特定出发时间,假设每个站的乘客的到达分布规律满足下面的分布:

在公式中,γu,μu和σu是每个站的乘客数量的基本参数,基本值如表1所示。

表1 各站客流需求的基本参数取值

显然,当确定优化时间间隔δ时,可以通过以下等式计算各站t(t∈[1,7200/δ])的乘客需求。

(18)

例如,假设δ=180s,将发送站1的基本参数代入等式(16),并且在第一时间间隔[0,180]内到达的乘客数量是65。

以1至7站为例,表2显示了前往每个站的乘客的概率ρuv。研究表明:3站的10%乘客可以通过地铁转移到1站。

算例参数取值和遗传算法参数取值情况分别见表3和表4。

表3 算例参数取值

表4 遗传算法参数取值

3.2 模型优化结果分析

作为优化结果和优化率的重要因素之一,优化时间间隔δ的调整对于整个结果有显著影响,基于此本文选择了三个不同的时间间隔(5s,10s和30s)来优化模型,收敛过程如图6所示,优化结果如表5所示。

表5 优化结果

图6 收敛过程

根据上述优化结果,可以得出以下结论:

①从图6可以看出,优化结果在53代后开始收敛。

②根据表5,在δ=5s的情况下,模型的最优解优化为566142元,比δ=10s时的最优解优化了2736元,比δ=30s时的最优解优化了12549元。在此,给出δ=5s时求得到的最优开行方案。

4 结论

(1)对于所建模型基于仿真的两步遗传算法,收敛性强,求解效率高。

(2)选择三个不同的时间间隔(5s,10s和30s)优化模型,优化结果在53代后开始收敛。在时间间隔为5s的情况下,模型的最优解优化为566142元,比时间间隔为10s时的最优解优化了2736元,比时间间隔为30s时的最优解优化了12549元,故时间间隔为5s时求得到的最优开行方案。

(3)通过对列车数量、车站人数和乘客等待时间进行敏感性分析,发现“小而高密度”列车运行计划可以平衡乘客和运营单位的利益;同时,较小的平台容量严重限制了城市轨道交通的服务水平,增加了城市轨道交通的运营成本;而且越小的平台容量就会导致越高的成本,包括运营成本和乘客等候的成本。

(4)有关部门根据所得最优方案可对列车开行方案进行优化,确定更加合理的列车开行方案(包括运营时间及交路和用车计划等),将会有效提高乘客出行效率,减少出发站每列列车的运营费用,提高了城市轨道交通服务水平,对城市轨道交通高质量发展起到推动作用。