流速对系泊球形潜体动力特性及尾涡结构的影响研究*
蒋济同, 刘瑞庆, 周献祥
(1. 中国海洋大学工程学院, 山东 青岛 266100; 2. 军事科学院国防工程研究院, 北京 100036)
随着油气资源消耗的日益增加,海洋资源的开发和利用受到越来越多国家的重视,大力发展海洋油气对于中国社会发展的需要和经济结构的调整都具有重要意义,而深海资源的开发离不开各类具备操纵性能的水下作业设备的支持[1]。
悬置海洋中部构筑物使用系泊缆固定在特定水深,不具备自主航行能力。可以为水下潜器提供燃料以提高水下作业设备的持久性,同时可以搭载传感器对海洋环境进行长期的监测,以及为深海活动提供设备上的支持,为人类进一步对深远海环境的勘察和油气等资源的开发和利用提供有力的支持。韦起贤[2]使用双向流固耦合的方法,对不同形状的潜体进行了动力响应分析并做了形状的优选。牛云龙[3]研究了影响潜体安全性和实用性的因素,并通过AQWA软件对三索三点和单索单点进行比较,分析不同的系泊方式对构筑物运动响应的影响。旷俊[4]使用AQWA软件对单索单点系泊球型构筑物进行了动力响应研究。由于势流是无旋性速度场,因此,基于势流理论的AQWA软件在计算绕流体在水流中的动力响应问题时忽略了多种因素的耦合影响,无法捕捉潜体运动时流场的变化和潜体的运动特性。
本文采用较为直观的在实验水池中进行模型试验的方法,以及目前发展比较成熟的计算流体力学的方法来研究球形潜体在不同流速下的运动响应问题。首先根据实验室条件设计了针对球形潜体模型的水动力试验,试验模型为3D打印的直径为0.2 m的球形潜体,系泊缆选用细软的高强度鱼线,鱼线质量与尺寸远小于球形潜体尺寸,所以在使用数值实验方法研究球形潜体的运动特性时不考虑系泊缆的影响。数值计算使用ANSYS软件的双向流固耦合模块,为了更广泛地研究流速对球形潜体运动特性的影响,在实验室0.3和0.5 m/s工况的基础上,数值实验增加了0.1、0.2和0.4 m/s三个工况。
1 三维绕流数值模拟
1.1 SST k-ω 湍流模型方程
CFD常用的湍流计算模型包括LES、k-ε、k-ω等。目前被广泛使用的大涡模拟法(LES)精度较高,是计算绕流模型比较理想的计算模型,然而存在计算效率低的问题。在近壁面问题的处理上,相对于k-ε模型采用壁面函数SSTk-ω模型在近壁面处采用k-ω,对边界层网格进行直接求解;主流区则采用k-ε,近壁面处理较好,能准确预测升力与阻力。所以在综合考虑计算效率和计算精度这两个因素后,本研究选择SSTk-ω湍流计算模型进行后续的计算。Menter[5]在标准k-ω模型中加入交叉扩散项,并在湍流黏度定义中考虑了湍流剪切应力的传递,得到了 SSTk-ω模型:
(1)

(2)
式中:Gk为湍动能生成项;Gω为比耗散率生成项;Yω和Yk分别为ω和k的耗散项;μ为来流动力黏性系数;Dω为交叉扩散项;ρ为来流密度[6]。
1.2 参数设置


图1 流体域
1.3 糙率设置
水动力试验方案中使用的模型根据糙率相似准则设计模型尺寸,数模糙率设置参考有机玻璃的糙率范围。购买一个糙率为0.008 5的标准有机玻璃材质模型,对试验模型进行砂纸打磨,使其糙率更加接近有机玻璃的糙率,比较两种不同材料的模型在水流作用下的运动响应和受力情况[4]。由图2(a)和(b)可知两种材料的球形潜体顺流向(x轴方向)和逆流向位移的误差均在10%以内,说明试验模型的糙率和有机玻璃模型的糙率是接近的。将试验模型的糙率认定为0.008 5,数值模型的糙率相应的设置为0.008 5。

((a)不同材料的球形潜体顺流向运动响应对比;(b)不同材料的球形潜体横流向运动响应对比。(a) Comparison of downstream motion responses of spherical submersibles made of different materials; (b) Comparison of cross flow motion responses of spherical submerged bodies made of different materials.)
1.4 重叠网格
本文研究的球形潜体运动问题包含了潜体的大幅度摆动和转动,之前的做法是使用传统动网格的方法计算,但是传统动网格在使用过程中需要频繁地使用平顺、铺层和网格重新生成这些操作,这些复杂操作在绕流固体位移过程中不仅要花费更多时间,而且容易产生计算不收敛问题[7],重叠网格方法的使用很大程度上解决了网格运动可能产生的这些问题,而且可以选择精度相对更高的六面体网格代替四面体网格,通过结构化网格划分来提高网格质量,进而提高计算精度,使绕流固体运动的计算更加高效和精确。Steger等[8]最早提出重叠网格,其方法是将网格分成贴体网格和背景网格两部分,两套网格重叠,且网格不用共点或共面。重叠网格的背景网格和贴体网格示例如图3(a)所示。

((a)重叠网格剖面;(b)不同网格数运动响应结果对比。 (a) Overlapping grid sections; (b) Comparison of motion response results with different grid numbers.)
为进一步减小网格对计算结果的影响并减轻计算负担,这里选用3套网格数量(432 325、632 253和833 625个六面体单元网格)进行结果对比。从图3(b)可知,40万个网格的计算结果与60万个网格的计算结果相差6%,而60万网格的计算结果同80万个网格的计算结果相差小于1%,说明60万个网格已经趋于收敛,因此下文的数值实验计算均使用60万个网格。
2 结果分析
2.1 顺流向与横流向运动响应幅值及均方根对比
本文用0.3和0.5 m/s两个试验工况的结果校正数值实验模型,并用校正后的计算模型对流速为0.1、0.2和0.4 m/s的工况进行计算。经计算,模型稳定后的试验结果和数值实验结果中顺流向平均位移分别为6.39和6.31 mm,两者平均位移吻合较好。由于双向流固耦合计算量较大,本文在模型试验与数值实验的潜体模型运动稳定后,各取20 s结果做比对,图4分别给出了工况为0.3和0.5 m/s时两者在顺流向及横流向上的运动响应。
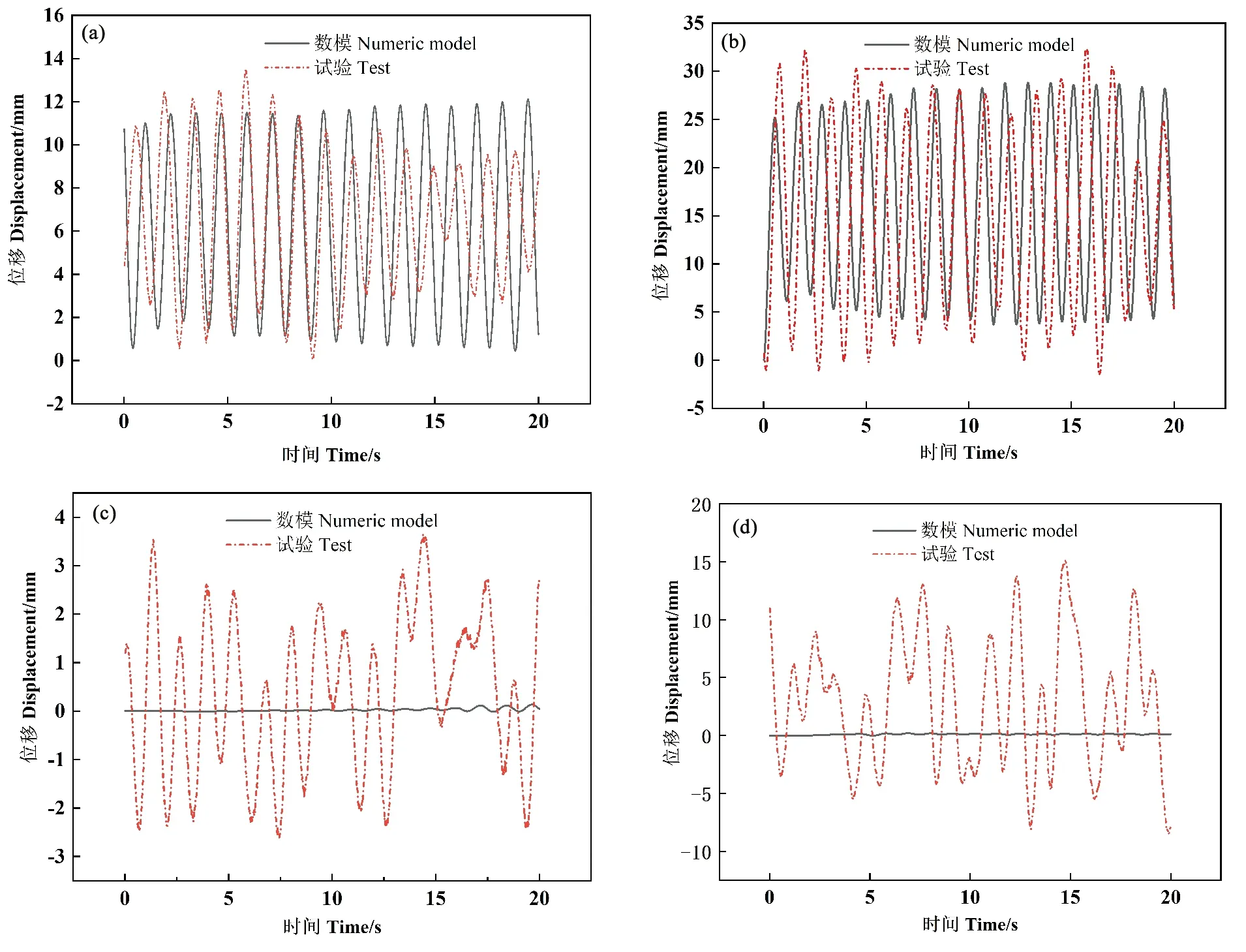
((a) 0.3 m/s顺流向运动响应对比; (b) 0.5 m/s顺流向运动响应对比; (c) 0.3 m/s横流向运动响应对比; (d) 0.5 m/s横流向运动响应对比。 (a) 0.3 m/s downstream motion response comparison; (b) 0.5 m/s downstream motion response comparison; (c) 0.3 m/s cross flow motion response comparison; (d) 0.5 m/s cross flow motion response comparison.)
图4(a)为潜体模型在顺流向上流速为0.3 m/s时数值实验结果和试验结果的比对,两者变化趋势保持一致,平均值相同,数值实验结果的运动幅值相对于试验结果要更加稳定,这是因为基于RANS方程的SSTk-ω湍流模型将非定常流转化为定常流问题,只能计算平均流动,不能计算流体的所有细节。图4(b)是顺流向上流速为0.5 m/s时数值实验结果和试验结果的对比,两者平均值大致相同,运动幅值也基本吻合。
图4(c)和图4(d)分别为模型在流速为0.3和0.5 m/s时横流向数值实验结果和试验结果的比对,2个流速下数值模拟的运动幅值均远小于试验结果。考虑到试验模型内部贴附的配重块不能均匀分布在球身上,这使得模型存在重心偏移,即圆球的重心和球心不重合,并且手工打磨抛光的球形潜体模型的外形、糙率和标准的数值模型存在一定误差。猜测是圆球重心偏移、几何中心偏移以及糙率的误差均影响了模型试验中潜体的横向位移,同时流速从0.3 m/s增大到0.5 m/s,又放大了这个偏差。针对这个猜测,建立了一个几何中心和重心偏移12%的模型,在流速为0.5 m/s工况下重新计算发现,横流向出现了小幅度位移,证实了圆球重心和几何中心的偏移会影响潜体的横向位移,但尚无法准确量化试验所用模型的重心和几何中心的偏移程度,以及糙率误差的大小,模拟无重心和几何中心的偏移潜体是研究潜体运动响应的一个阶段性工作,下一步工作将研究数值模型的重心和几何中心的偏移计算,并在之后的模型试验设计中要着重考虑试验模型制作的重心和几何中心的偏移问题。
为了更直观地对比数值实验与试验两者的运动幅值结果,将5个工况的计算结果一并进行均方根处理并分析。图5(a)为顺流向运动无量纲均方根幅值,数值实验顺流向的结果与试验结果走势相同,随着流速的增大总体呈增大趋势,并且随着流速的增大无量纲均方根幅值的增幅变大。其中:在流速为0.3 m/s工况下数值模拟结果为0.19,略大于实验结果的0.17;在流速为0.5 m/s工况下数值实验结果为0.42,小于实验结果的0.51。图5(b)横流向无量纲均方根幅值,数值实验结果靠近0附近,试验结果分别为0.08和0.27,均大于0,这是因为在前期制作试验模型过程中,给模型加的配重块不能均匀分布在球身,导致模型在横流向上的运动偏向一侧。
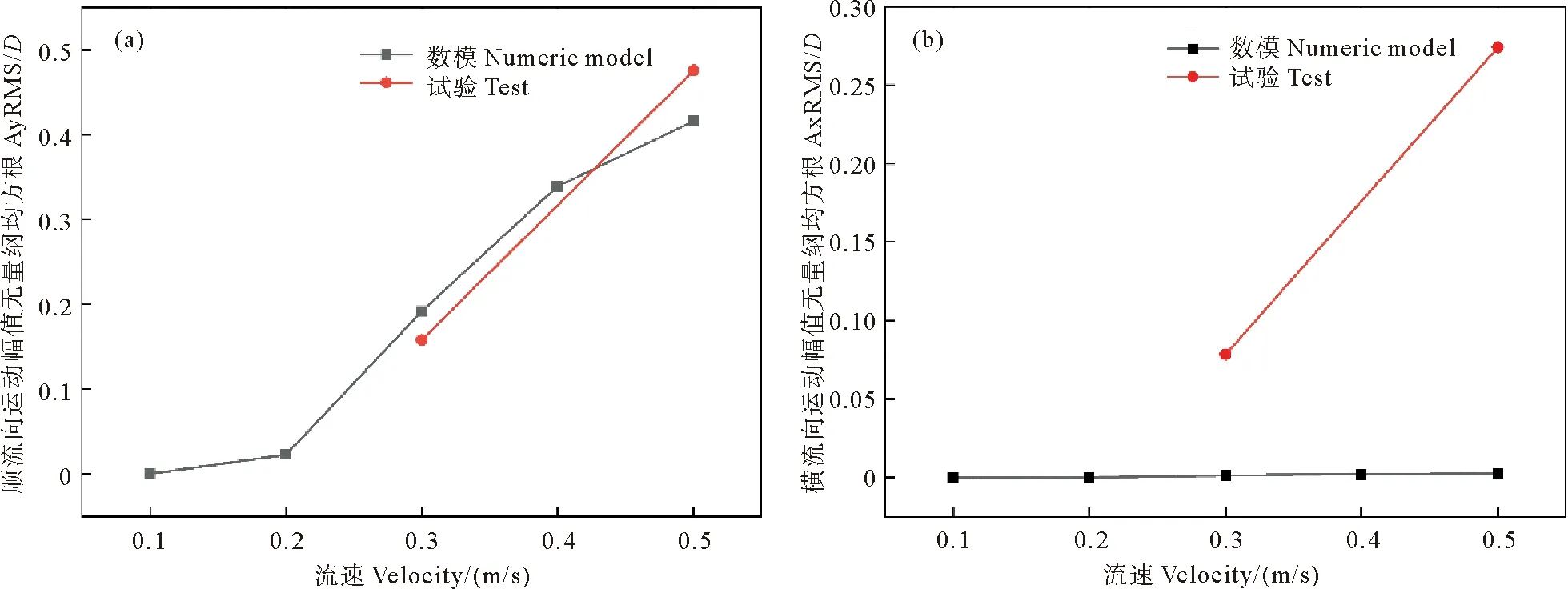
((a)顺流向运动幅值无量纲均方根;(b) 横流向运动幅值无量纲均方根。(a)Dimensionless root mean square of down stream motion amplitude; (b) Cross flow motion amplitude dimensionless root mean square.)
2.2 圆周压力系数
图6给出了在Z=0高度处截取压力系数沿圆周的分布特性。图中θ为XY平面方位角,球体的前驻点为0°,顺时针方向为正方向,后驻点为180°。由于模型沿着顺流向的中心线是对称的,所以各工况的压力分布也是沿着中心线对称分布的。各工况的最高压力出现在0°处,随着角度的增加压力急剧下降,在迎流面上形成正压力梯度,使表面的边界层加速流动,在70°~90°之间表面压力达到最小,速度达到最大,称为顺压区。经过这个区间后外部的势流及边界层开始减速加压,在剪应力和逆向压力梯度的双重作用下边界层流体动能减小,开始出现边界层分离,称为逆压区。随着流速的增加,表面分离点滞后,具体表现为当流速为0.1、0.2和0.3 m/s时压力最小点均出现在78°的位置,当流速为0.4和0.5 m/s时压力最小点均推后到85°处,分离点位置的变化影响着球形潜体的阻力,球形潜体的阻力主要包括摩擦阻力和压差阻力,其中压差阻力要比摩擦阻力大得多[9]。分离点位置越靠后,球形潜体的前后压差就越小。根据图6可知,随着流速的增大,分离点呈后移趋势,即前后压差减小,更易克服逆压梯度。
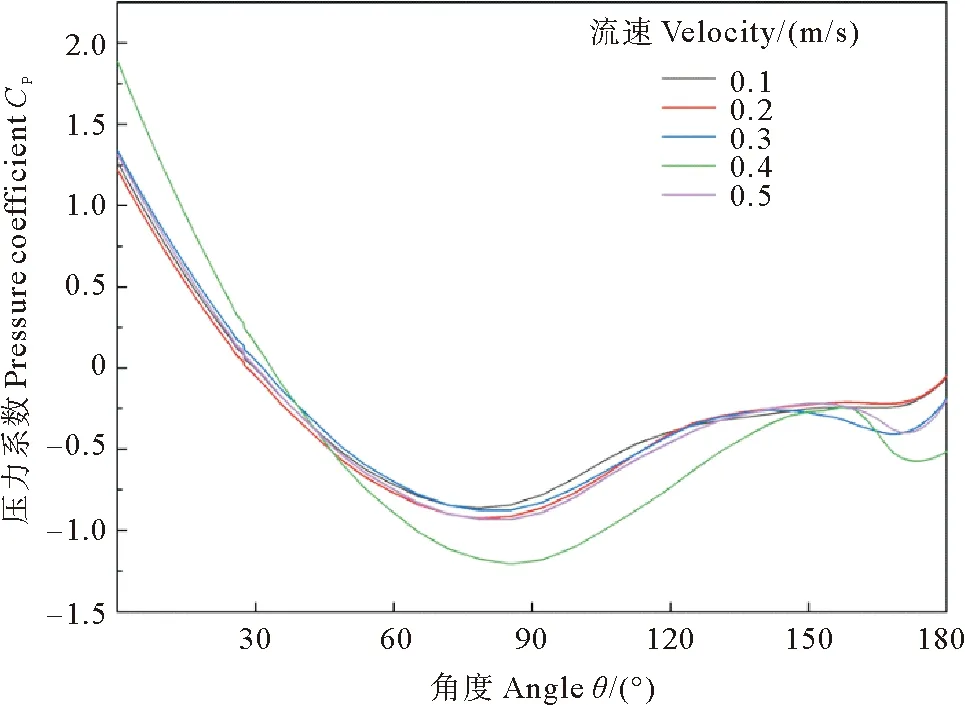
(黑色线代表0.1 m/s工况,橙色线代表0.2 m/s工况,蓝色线代表0.3 m/s工况,绿色线代表0.4 m/s工况,紫色线代表0.5 m/s工况。The black line represents 0.1 m/s, the orange line represents 0.2 m/s, the blue line represents 0.3 m/s, the green line represents 0.4 m/s, and the purple line represents 0.5 m/s.)
2.3 St数


图7 St数随速度的变化
2.4 尾涡形态分析


(横坐标表示流场顺流向尺寸Y与潜体直径D的比值:Y/D;纵坐标表示流场横流向尺寸X与潜体直径D的比值:X/D。The horizontal axis represents the ratio of the downstream dimension Y of the flow field to the diameter D of the submerged body: Y/D; The vertical axis represents the ratio of the transverse dimension X of the flow field to the diameter D of the submerged body: X/D.)

(横坐标表示流场顺流向尺寸Y与潜体直径D的比值:Y/D;纵坐标表示顺流向流速Uy与入口初始流速U0的比值:Uy/U0。The horizontal axis represents the ratio of the downstream dimension Y of the flow field to the diameter D of the submerged body: Y/D; The vertical axis represents the ratio of the downstream flow velocity Uy to the initial inlet flow velocity U0: Uy/U0.)
3 结论
(1)顺流向上模型的运动响应数值实验结果同试验结果吻合很好,模型的运动幅值无量纲均方根同数值模拟结果基本一致,两者走势相同,随着流速的增大总体呈增大趋势。
(2)随着流速增大,模型的分离点呈后移趋势,且在0.3和0.4 m/s流速下分离角骤增,分离点后移,即前后压差减小,随着流速的增加球形潜体更易克服逆压梯度。
(3)随着流速的增加St数呈下降趋势,且在0.3和0.5 m/s工况处的数值模拟结果和试验结果一致。由于雷诺数在103~104范围内高频率(涡脱落的频率)的存在直到6×104[10],流速从0.2 m/s增大到0.3 m/s时,St数出现骤降。
(4)模型分离点随着流速的增大而后退,即涡结构从圆球表面脱离的位置更加靠后,这使得涡结构的形状发生变化,表现为0.5 m/s工况下涡结构的初始形态由开始的圆环状被拖拽成水滴状。脱落的涡结构之间的间隔随着流速增大而变大,更大的流速产生更大的涡量,更大涡量的涡结构可以传播到更远的位置,其中,在顺流向的中轴线上,每个涡结构的核心处也是流速的极大值。
- 中国海洋大学学报(自然科学版)的其它文章
- 海洋骨料混凝土材料与结构性能研究进展*
- 考虑粗糙度影响的单圆角柱体水动力特性影响研究*

