单步无条件稳定结构动力求解隐式算法

李常青 ，钟志强，蒋丽忠 ，聂磊鑫

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程研究中心，湖南 长沙 410075)

在结构动力问题中，直接积分法是一个被广泛研究的课题，并在结构动力反应计算中得到广泛应用[1]。根据计算步的多少，直接积分法分为单步法、两步法和多步法。单步法只需要知道上一步的运动状态，即可求得本步的运动状态，而两步法和多步法的求解分别需要2个时刻和多个时刻的运动情况。根据运动方程的耦合情况，直接积分法分为显式法和隐式法。显式法不需要联立求解方程组，根据已知的信息就能求得该时刻的解，具有更高的计算效率；而隐式法需要求解耦联的方程组，计算工作量大。但是显式法通常是条件稳定的，当时间步长超过某一临界值时，数值解的计算误差会瞬间增大并趋于无穷值；而隐式法大多是无条件稳定的，对时间步长的选择没有限制，适用范围更广。中心差分法是一种经典的显式法，在很多情况下仍有较好的计算效果，并催生出许多优秀的显式算法[2-5]。本文关注隐式算法的发展、研究和应用。比较有代表性的隐式算法有Newmark-β法[6]，Houbolt 法[7]，Wilson-θ法[8]，HHT-α法[9]，WBZ-α法[10]，Generalized-α法[11]。这些算法在稳定性、精度、数值阻尼和超调特性上的表现各不相同。Newmark 平均加速度法具有较好的计算精度，但是没有数值阻尼，在计算时由于高频响应的影响可能会产生数值振荡。Houbolt法的高频响应总是渐进衰减为0，不能调控数值阻尼，同时需要借助其他方法来起步。Wilson-θ法的谱半径在中频段会发生突变，使得中频段的数值阻尼大于高频段的数值阻尼，同时在位移和速度上会产生明显的超调现象。HHT-α法对数值耗散的调控比较有限，不能最大程度地滤除高频分量。WBZ-α法在满足2 阶精度时是条件稳定的，并且具有不利的超调特性。Generalized-α法能有效地调控高频耗散并对低频响应的耗散较小，但是加速度是1阶收敛的。上述算法有些虽是自启动的，但在给定初始位移和初始速度的基础上，需要额外进行初始加速度的计算，而初始加速度的计算对加速度精度有较大的影响[12-13]。LI 等[14]认为真正自启动的算法是不需要初始加速度计算的，目前此类算法的研究取得了一定的进展。SOARES 等[15-16]提出的算法具有无条件稳定性和可控的数值阻尼，但存在不利的超调特性，无法输出加速度响应。KIM[17]的算法即使对于无阻尼结构求得的加速度都只有1阶精度。这些算法都有一些不理想的数值性质，因此有必要继续开展数值算法的研究，新算法应在稳定性、精度、数值阻尼、超调和自启动上有良好的表现。本文基于量纲分析的思想，基于相关文献[18-20]中的思路，提出一种单步无条件稳定隐式算法，通过理论分析和数值算例揭示其数值特性，为结构动力问题的求解提供新方法。

1 隐式算法的格式

1.1 隐式算法的初步格式

直接积分法研究的是离散时间点上的值，单自由度线性结构的动力方程为：

其中：m，c和k分别为结构的质量、阻尼和刚度；at，vt，ut分别表示结构在t时刻的加速度、速度和位移；ft表示结构在t时刻所受的外力。

构造位移和速度的函数关系式，假设：

其中：Δt表示积分时间步长；ut+Δt，vt+Δt和ft+Δt分别为结构在t+Δt时刻的位移、速度和所受的外力。根据国际单位制中的7 个基本单位，选取t时刻位移ut，时间步长Δt和质量m作为基本量，并根据Π定理[21]，对方程(2)和(3)进行无量纲化处理，表示为：

其中：cΔt/m和kΔt2/m是表示结构材料属性的参数。基于文献[18-20]的思路，引入系数ri(i=1，2，…，11) 和si(i=1，2…，11)，将方程(4)和(5)表示为：

对方程(6)和(7)化简可得：

其中：常系数bi=ri+1/r1(i=1，2，…，10)，hi=si+1/s1(i=1，2，…，10)，方程(8)和(9)即为新算法的基本格式。

1.2 待定系数的初步确定

位移和速度在t+Δt时刻的局部截断误差可表示为：

其中：u(t+Δt)和v(t+Δt)分别表示结构位移和速度在t+Δt时刻的精确解；ut+Δt和vt+Δt表示位移和速度在t+Δt时刻的数值解。基于精确解得到结构的动力平衡方程为：

将t+Δt时刻的位移，速度和加速度在t时刻泰勒展开，可得：

对方程(8)和(9)等式右边的项进行处理，令：

将方程(8)和(9)以及方程(12)～(17)代入方程(10)和(11)，并化简为：

其中：di(i=0，1，…)和qi(i=0，1，…)是关于m，c，k等量的函数关系式，有：

当位移和速度有n阶精度时，则有：

根据方程(22)，当位移和速度具有2 阶精度时，有：

方程(23)只有满足以下条件时才成立，即：

解方程(24)可得：

则方程(8)和(9)可化为：

根据方程(26)和(27)可知，位移和速度递推格式中不含加速度项，其在t+Δt时刻的响应由t时刻的位移、速度和外力以及t+Δt时刻的外力所决定，因此可以说本算法是真正自启动的算法。此外，如果需要得到加速度响应，可以根据各个时刻的动力平衡条件求得。t+Δt时刻的平衡条件为：

当加速度有n阶精度时，有：

加速度在t+Δt时刻的局部截断误差可表示为：

其中：ji(i=1，2，3，4)是关于m，c，k的函数关系式，则：

根据方程(29)，因此加速度具有2 阶精度，方程(26)～(28)即为本算法的3 个基本公式，方程中的参数取决于算法的数值特性。

2 数值特性

2.1 收敛性

2.1.1 稳定性

以单自由度系统为基本对象，分析算法的稳定性，其t时刻的运动方程表示为：

其中：ξ为结构的阻尼比；w为结构的固有频率。将方程(26)和(27)表示为递推形式：

其中：A和L分别表示算法的放大矩阵和荷载矩阵。矩阵A和L中的系数表示如下：

其中：Ω=wΔt。放大矩阵A的特征方程为：

其中：E为2 阶单位矩阵；λ为放大矩阵A的特征值；A1=(A11+A22)/2；A2=A11A22-A12A21。A1和A2具体如下：

放大矩阵A的谱半径为：

算法稳定性条件为ρ(A)≤1。HILBER 等[22]给出了算法实现无条件稳定的条件，即：

求解方程(39)，可得：

2.1.2 相容性

直接积分法的相容性可以通过其局部截断误差[23]来分析，定义为：

将u(t+Δt)和u(t-Δt)在t时刻泰勒展开，并根据t时刻的平衡方程ma(t)+cv(t)+ku(t)=0，方程(41)可化为：

其中：gi(i=1，2，3，4)为w和ξ的函数关系式。

由方程(42)可知，e(t)为Δt的2 阶小量，说明本算法是2 阶相容的。根据Lax 定理，当算法既具有相容性又具有稳定性，则算法收敛。因此，本算法收敛，算法的精度阶为相容的阶数，即具有2阶收敛精度。

2.2 计算精度

在结构动力问题中，直接积分法对结构体系的运动进行离散化，使结构的运动方程在离散的时间点上满足即可。然而，结构在离散化过程中所产生的高阶模态往往是不准确的，不能代表结构本身的运动状况，因此有必要引入数值阻尼滤除高频响应的贡献，同时也要尽可能地降低对低频分量的影响。文献[11]中指出，当放大矩阵的特征值为一对共轭复根时，算法对高阶模态的耗散最大，同时随着Ω 趋于无穷大，特征值应为实数。为了使本算法具有耗散特性，放大矩阵A的特征值可表示为：

求解方程(44)，可得：

放大矩阵A的谱半径可表示为：

为了调节高频耗散，引入参数：

其中：λ∞为非正数。ρ∞的取值影响着算法对高频耗散的能力，ρ∞越小，算法对高频耗散越大，当ρ∞=0，算法对高频分量的衰减最大。

在2.1 节通过对收敛性分析可知，本算法具有2 阶理论精度。刘祥庆等[24]指出在实际计算中算法所表现出来的精度称为计算精度，可以通过振幅衰减AD和周期延长PE来衡量。本文以单自由度有阻尼自由振动为例，给出了其计算公式：

为了分析参数b5和h8对计算精度的影响，考虑无阻尼条件下，ρ∞分别取0.25，0.5 以及0.75，比较Δt/T=0.3 时振幅衰减AD和周期延长PE的值，将振幅衰减和周期延长为最小值时所对应的b5和h8的取值记录在表1 中。从表1 数据可知，当ρ∞取不同值时，振幅衰减和周期延长总是同时达到最小值，此时b5和h8的值相等，因此为了使算法具有最高的计算精度，取h8=b5。

表1 振幅衰减和周期延长取最小值时b5和h8的取值Table 1 Values of b5 and h8 when the amplitude decay and period elongation take the minimum value

将h8=b5代入方程(40)和(45)中，可得：

对有阻尼情况下的周期延长进行分析可知，当b4=1/(4+8b5)，b10=1/4 时，周期误差最小。因此，将各参数的取值用ρ∞表示为：

2.3 频谱分析

对算法在无阻尼和有阻尼情况下的频谱特性进行分析，如图1 和图2 所示。从图1 和图2 中可以看到无论是否存在阻尼，本算法都是无条件稳定的，并能够调节数值阻尼。在图1中，对无阻尼情况下本算法与Newmak 平均加速度法、Houbolt法和Wilson-θ法的频谱特性进行比较。其中，Newmark 平均加速度法与本算法在ρ∞=1 时的数值特性完全相同；Houbolt 法虽然具有耗散能力，其谱半径曲线与本算法ρ∞=0 时接近，其高频谱半径趋于0，但对低频分量的耗散较大，同时振幅衰减和周期延长也较大，计算精度最差；Wilson-θ法在中频段的数值阻尼较大，对低频分量的影响较大，对高频分量的耗散能力较差，但其计算精度优于Houbolt 法。本算法通过参数ρ∞调节高频耗散，在引入数值阻尼的同时又能较大程度地降低数值阻尼对低频响应的影响，在不需要数值阻尼时与Newmark 平均加速度法等价，实现零振幅衰减和最小的周期误差。当ρ∞=1 时，本算法的位移、速度和加速度递推格式与Newmark 平均加速度法完全相同。

图1 不同算法的频谱特性(ξ=0)Fig.1 Spectrum characteristics of different algorithms (ξ=0)

图2 新算法与Generalized-α法的频谱特性(ξ=0.05)Fig.2 Spectrum characteristics of the new algorithm and the Generalized-α method (ξ=0.05)

在图2 中，对有阻尼情况下Generalized-α法与本算法的频谱特性进行比较。在ρ∞=1 时，本算法与Generalized-α法的谱半径相接近，计算精度完全相同；在ρ∞=0.5 时，Generalized-α法的频谱特性优于本算法；在ρ∞=0 时，本算法对低频分量的影响更小，同时具有更好的计算精度。因此，对多自由度体系而言，如果需要最大程度地衰减高频分量，获得更精确的结果，本算法优于Generalized-α法。

2.4 超调特性

当选取较大的时间步长，使得初始几个时间步的计算结果被明显放大的现象称为超调[23]。谱半径稳定性条件决定算法在长时间内的稳定性，超调特性会影响算法在短时间的稳定，必须防止这种现象的发生。本文通过对第1个时间步长内的结果进行分析，说明本算法的超调特性。

考虑单自由度有阻尼体系做自由振动，对于给定的位移和速度初始条件，当Ω →∞，本算法在第1个时间步的位移、速度和加速度可表示为：

由方程(54)可知，第1 个时间步的计算结果与时间步长无关，说明本算法的位移、速度和加速度都不会发生超调。

为了比较算法的数值特性，定义绝对误差：

式中：x(i)表示i时刻的精确解；xi表示i时刻的数值解；x可取为u，v，a。

对该单自由度体系，阻尼比取ξ=0.5，自振频率ω=2π，初始条件u0=1 m，v0=1 m/s，第1 个时间步长的计算结果如图3 所示。从图3 可知，对于给定的ρ∞，随着Δt的增大，位移、速度和加速度的绝对误差都趋于有限值，说明本算法不会出现超调行为，与理论分析结果相一致。

图3 第1个时间步相对于积分步长Δt的绝对误差Fig.3 Absolute error in the first time step versus the integration stepΔt

2.5 计算流程

对于多自由体系，本算法的具体计算过程如下。

1) 选取时间步长Δt和谱半径趋于无穷大的值ρ∞，计算参数：

2) 确定运动初始值{u}0和{v}0。

3) 形成刚度矩阵[K]，质量矩阵[M]，阻尼矩阵[C]。

4) 形成等效矩阵，即：

5) 计算t+Δt时刻的等效荷载，为：

6) 计算t+Δt时刻的位移和速度，即：

7) 根据需要计算t+Δt时刻的加速度：

循环计算上述步骤5～7，即可得到线弹性体系在任一时刻的位移、速度和加速度。

3 算例分析

在本节中，通过3个数值算例对本算法的数值特性进行分析，揭示本算法在精度和可控数值阻尼的优越性。

3.1 算例1

以单自由度无阻尼结构为例，分析算法在无阻尼条件下的数值行为。取结构质量m=1 kg，结构刚度k=16 N/m，结构自振周期T=π/2 s，初始条件u0=1 m，v0=1 m/s，时间步长Δt=1/20T，分析不同算法的绝对误差，如图4 所示。由于Houbolt法无法实现自启动，本文均采用中心差分法计算其前2 个时间步的解。从图4 可知，Newmark 平均加速度法与本算法在ρ∞=0 时的计算结果完全相同；Houbolt 法的位移、速度和加速度绝对误差都是最大的，其计算精度最差；Wilson-θ法得到的结果介于本算法ρ∞=0.25 和ρ∞=0.5 之间，其误差较大。图4的结果与频谱分析的理论结果相一致，表明本算法通过调节参数ρ∞，不仅能使算法转化为Newmark 平均加速度法，同时优于Houbolt 法和Wilson-θ法。

图4 不同算法的绝对误差Fig.4 Absolute error of different algorithms

3.2 算例2

以单自由度有阻尼结构为例，比较本算法与Generalized-α 法的数值特性。取结构质量m=1 kg，结构刚度k=5 N/m，结构自振周期阻尼比，结构外力ft=sin(2t)，初始条件u0=57/65 m，v0=2/65 m/s。结构的位移精确解可表示为：

为了比较算法的数值特性，定义全局误差：

式中：Nt表示总计算时间；x(i)表示i时刻的精确解；xi表示i时刻的数值解。x可取为u，v，a。

总计算时间取Nt=10T，得到全局误差随时间步长的变化关系，如图5 所示。从图5 可知，对于有阻尼结构，无论ρ∞取何值，本算法的位移、速度和加速度都具有2 阶收敛精度，同时Generalized-α法的位移和速度也具有2 阶收敛精度，而Generalized-α法只有当ρ∞=1 时加速度才具有2 阶收敛精度，其他情况下只有1 阶收敛精度。此外，当ρ∞=0，本算法计算得到的全局误差明显小于Generalized-α法；当ρ∞=0.5时，2种算法的位移和速度全局误差相差不大，而Generalized-α法的加速度全局误差明显偏大；当ρ∞=1 时，2 种算法的位移、速度和加速度全局误差十分接近。整体而言，本算法计算得到的加速度精度更高，误差更小，同时当ρ∞的取值接近于0，本算法的数值性能明显优于Generalized-α法。

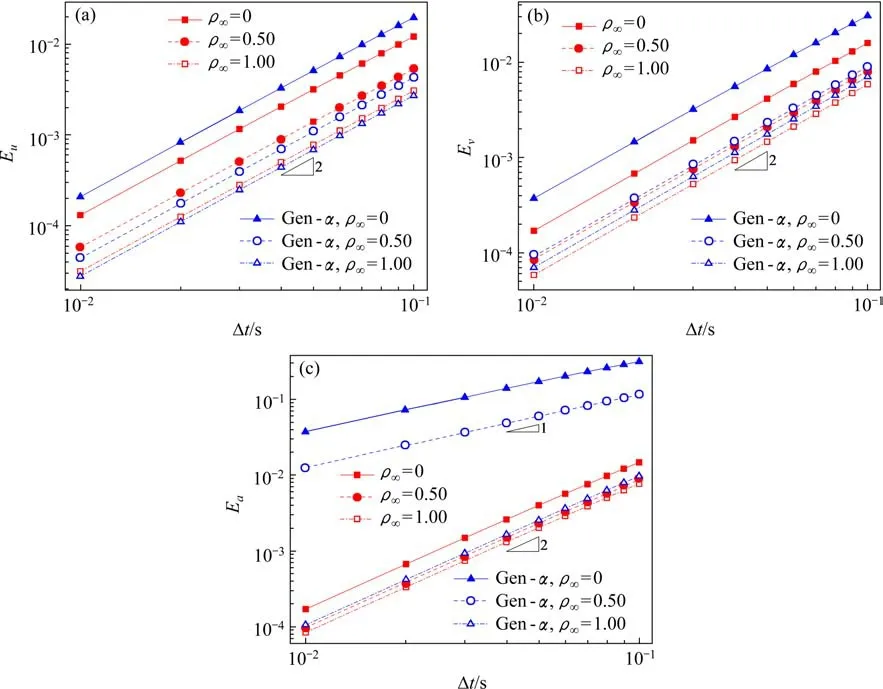
图5 新算法与Generalized-α法的全局误差Fig.5 Global error of the new algorithm and the Generalized-α method

3.3 算例3

以悬臂杆[25]为对象，在t=0 时施加端部荷载F(t)，如图6所示。其位移u(x，t)运动方程为：

图6 受端部荷载的悬臂杆Fig.6 A clamped-free bar excited by end load

式中：E为弹性模量；A为截面面积；ρ为质量密度。约束条件为：

式中：L为杆件长度。将杆件离散为N个等长的2节点单元，单元长度le=L/N，采用一致质量矩阵，其单元刚度矩阵和单元质量矩阵为：

此算例中L=200 m，F(t)=1×104N，E=5×107Pa，A=1 m2，ρ=8×10-4kg/m3，N=1 000，时间步长Δt=4.72×10-7s。

采用Newmark 平均加速度法求解，得到杆件中间节点位移和速度随时间的变化情况，如图7所示，图中Reference 表示理论解。图7 中位移和速度均产生数值振荡，有必要引入数值阻尼来抑制杂散模态[26]。采用Generalized-α法和本算法在ρ∞=0.75时求解，结果如图8所示。与Newmark平均加速度法相比，2 种具有数值阻尼的算法都能提供更精确的位移解，都能在较大程度上抑制数值振荡，明显提高速度的求解精度，但本算法在位移和速度的求解中表现出更好的计算精度，计算结果更接近理论解。说明本算法通过引入数值阻尼，在滤除高频响应的同时，更大程度地保留低阶振型的贡献，具有更优的数值特性。

图7 Newmark平均加速度法的响应Fig.7 Response of the Newmark average acceleration method

图8 新算法与Generalized-α法的响应Fig.8 Response of the new algorithm and the Generalized-α method

4 结论

1) 本文算法具有无条件稳定、2 阶精度和无超调特性，并通过调整参数值能转变为Newmark 平均加速度法，同时优于Houbolt法和Wilson-θ法。

2) 本文算法不需要加速度参与，能实现真正的自启动，并能提供2阶精度加速度输出。

3) 本文算法具有可控数值阻尼特性，与Generalized-α法相比，该算法在有阻尼条件下，位移、速度和加速度均有2阶精度，并能提供更好的计算精度。