大跨径悬索桥涡激共振试验研究
程 斌 林贤光
(武汉城市职业学院,湖北 武汉 430064)
0 引言
大跨径悬索桥主梁具有质量相对较轻、自振频率小、阻尼比低等特点,在运营阶段常遇风速下易发生涡激共振现象,振动幅度较小不易察觉,仅在特殊条件下会产生较大振幅,引起桥梁结构疲劳等问题,同时会影响行车体验感、舒适性,易诱发交通安全事故。因此,通过多阶涡激共振振幅相等的气弹模型风洞试验以及多阶涡激共振振幅实桥验证,总结出大跨度悬索桥涡激共振的规律,可以有效指导今后超大跨度桥梁的抗风设计,提高桥梁的使用舒适性及安全性。
1 悬索桥的多阶模态涡激共振问题
1.1 涡激共振概念
众所周知,当气流流经钝体断面时,在断面两侧就会出现交替脱落的漩涡,交替脱落的漩涡引起结构物表面的压力周期性变化,从而在结构上产生周期性变化的竖向脉动力(压力差),也称为升力[1],如图1 所示。当升力的频率接近于结构的某一阶模态频率时,就会发生涡激共振,可能引起大幅震动。通常涡激共振是单个模态的共振响应[2]。

图1 涡激共振图
漩涡脱落频率、风速及断面尺寸之间存在以下关系:
式中:f——漩涡脱落频率;
D——钝体断面迎风面尺寸;
U——风速;
St——Strouhal 数。St主要由断面外形决定:对于圆柱体,St约为0.2;对于接近流线型的钢箱梁,St数在0.08~0.12之间。
基于该公式,可以计算出桥梁发生涡激共振时风速,对于大跨径桥梁,可以以频率在0.2~0.3Hz 来估算,梁高按3.5m计算,相对应的钢箱梁桥的涡激共振风速U=fD/St=(0.2~0.3)×3.5/0.1=7.0~10.5m/s,进一步分析可知,桥梁的跨度越小,频率就越高,起振的风速就越高,也就不容易出现涡激共振现象。
1.2 涡激共振特征
涡激共振主要有4个方面的特征[3]:
(1)在较低风速下发生的有限振幅振动,兼有自激振动和强迫振动的特征;
(2)只在某一特定风速区间内发生,称为锁定现象,如图2所示;
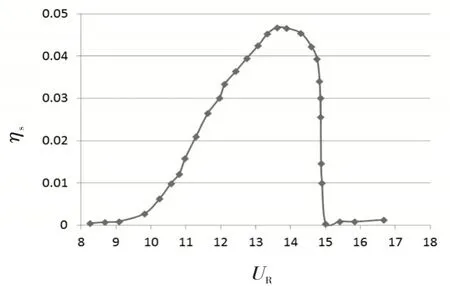
图2 无量纲风速-涡激共振振幅图
(3)涡激共振最大振幅与气动参数以及结构参数有关(模态阻尼和质量);
(4)涡激振动可以激起弯曲振动,也可以激起扭转振动。
1.3 悬索桥的多阶模态涡激共振问题
大跨度悬索桥竖弯模态密集、频率低,在0.1~0.7Hz范围内有很多阶竖弯模态,相应起振风速U=10fD=3.5~23m/s。
在行车风速范围内,随着风速的增加就会出现多个模态的涡激共振。在一个特定的分数对应某一个模态的振动。随风速的增加,相继有多个模态出现涡激共振,一个特定风速对应一个模态的涡激共振。
在工程实践中,已经观测多座钢箱梁悬索桥有多阶竖向模态涡激共振现象,例如我国某跨海大桥的涡激共振模态的主要频率范围在0.2~0.4Hz 左右,起振风速在6~12m/s范围内。
悬索桥竖弯模态频率密集,在常遇风速下容易出现多个模态的涡激共振。但现有的规范只针对一阶模态(通常是低阶模态)进行研究。高阶模态振动时,相同振幅下加速度响应更大,引起的结构应力也更大,对结构更加不利[4]。
2 悬索桥多阶涡激共振的理论与试验技术
2.1 多阶模态涡激共振振幅预测问题理论分析
桥梁风洞试验中,通常采用主梁节段模型来预测涡激共振,节段模型也是针对某一个模态进行[5],如果存在多个模态,应该预测各个模态的涡激共振幅值。
基于风洞试验预测涡激共振,采用线性涡激力模型论述多阶模态,涡激力作用下的结构动力学方程如式(2)。
右边是气动力,由两部分组成,第一项是自激力,第二项是涡激力,是一个强迫力。Y1、Y2为与断面形状有关的气动力系数,CL为动升力系数,可通过节段模型风洞试验来确定。
由结构动力学方程可以得到,无量纲振幅Y/D为:
若Y1=Y2=0,经验线性涡激振子模型退化为简谐涡激力模型。此时,无量纲振幅简化为:
由公式(4)悬索桥多阶模态振幅特征如下:
(1)涡激共振最大振幅不仅与断面气动外形有关,还与各阶模态的振型阻尼和质量有关;
(2)如果各阶模态的阻尼比相等,模态质量相等,那么它们的涡激共振振幅也就相等。
悬索桥基本满足上述条件,所以可以得到悬索桥各阶模态涡激共振振幅相等。
2.2 多阶涡激共振振幅相等的气弹模型风洞试验验证
2.2.1 气弹模型
为了验证上述理论方法,必须制作一个可以模拟多个模态密集分布的气弹模型,用气弹试验来验证。现有的气弹模型包括两类。
第一类是传统悬索桥气弹模型,从理论上来说是应该具备这一性质,但实际上因缩尺比太小、干扰因素太多而无法做到,而且一般只能模拟每个方向的2~3个模态。传统的悬索桥气弹模型无法完成高阶模态的模拟。
第二类是拉条模型,忽略了塔和缆索系统,制作比较容易,由于拉条模型的刚度由两条平行的张紧的钢丝提供,它的高阶频率分布按自然数增加,即n阶模态的频率是一阶模态频率的n倍,因此,拉条模型不能模拟悬索桥的多模态密集分布特性。
为了避开塔和缆索系统干扰,单纯研究加劲梁的高阶模态涡激共振,采用多点弹性支承连续梁的气弹模型,宽高比为6 的多点弹性支撑连续梁气弹模型如图3所示。

图3 多点弹性支撑连续梁气弹模型图
2.2.2 模型设计方法
已知参数: 频率, 振型ϕr(x) = sinrπx/L(r=1,2,......,m)
未知参数:弹簧刚度Ki,i=1,2,…(N+1)/2。
第r阶模态的广义刚度和广义质量为:
依据公式(5)、(6),可以建立方程组来确定未知弹簧的刚度。
动力特性验证有两种方法:
(1)采用激振器测定各阶模态的频响函数;
(2)自由衰减响应,气弹模型加速度传感器布置如图4所示。

图4 气弹模型加速度传感器布置图
通过测定前4阶模态的频率响应函数如图5所示。利用频率响应函数,可以得到它的模态阻尼比,如表1所示。
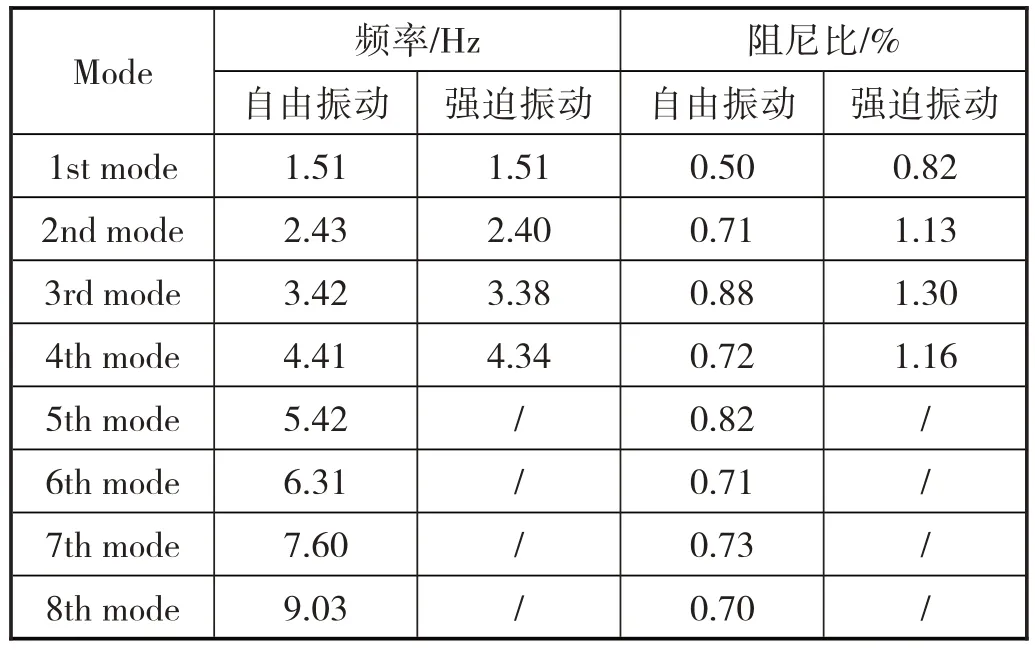
表1 气弹模型的实测频率与阻尼比对比
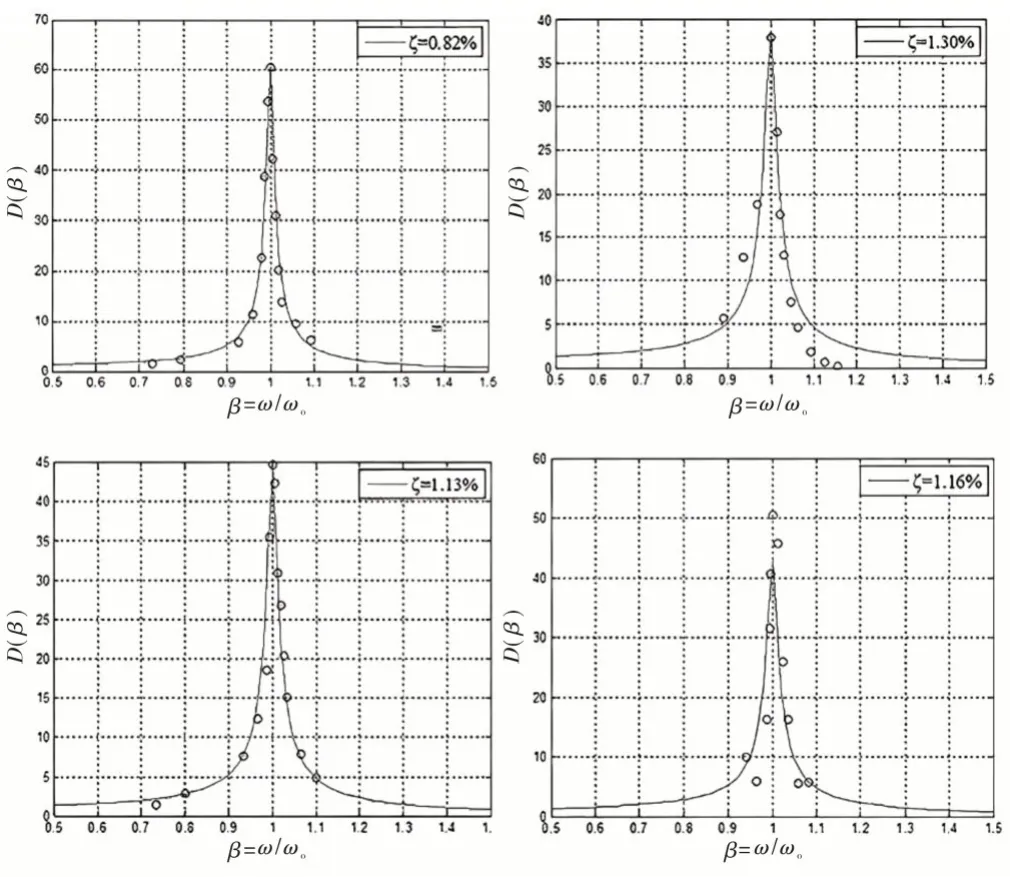
图5 前4阶模态的频率响应函数
基于该模型,测定各阶模态的涡激共振情况,高阶模态的涡激共振振幅基本相等;低阶模态振幅偏小,主要原因是紊流强度大则涡激共振振幅减小。如果扣除紊流影响,可以认为不同模态的振幅相同,如图6所示。
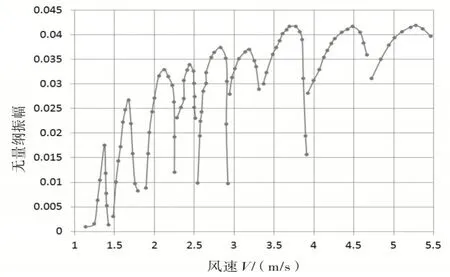
图6 无量纲化竖弯涡激共振振幅-风速曲线
2.3 多阶涡激共振振幅实桥验证
2.3.1 塔科马老桥风毁前的多阶模态涡激共振
塔科马老桥是验证多阶模态涡激共振的一个典型事例。塔科马老桥是因为颤振而损毁,但从它建成通车到发生风毁前,发生了将近4 个月不同模态的竖向涡激共振。通过整理塔科马老桥涡激共振的振幅,可以进一步研究多阶模态涡激共振的情况。
塔科马老桥是一座主跨853m 的悬索桥,桥宽11.9m、梁高2.45m、垂跨比1/12。从该桥报告的监测数据中整理出各阶模态的涡激共振振幅,并将对称模态和反对称模态进行分类处理(表2、表3)。从表中可见,在对称竖弯模态涡激共振振幅中,最大双边振幅达到了91cm;反对称竖弯模态涡激共振振幅中,最大双边振幅达到90~92cm 之间。从塔科马老桥实测的大量数据看,各阶模态的振幅基本相同,高阶模态振幅甚至略大于低阶模态振幅。
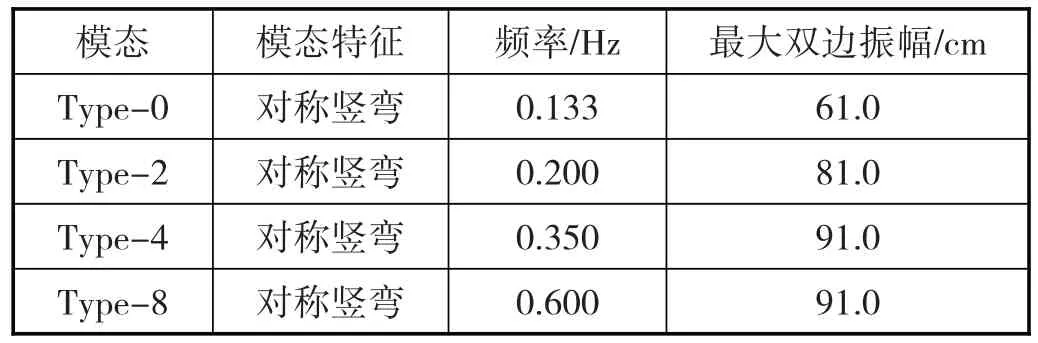
表2 对称竖弯模态涡激共振振幅
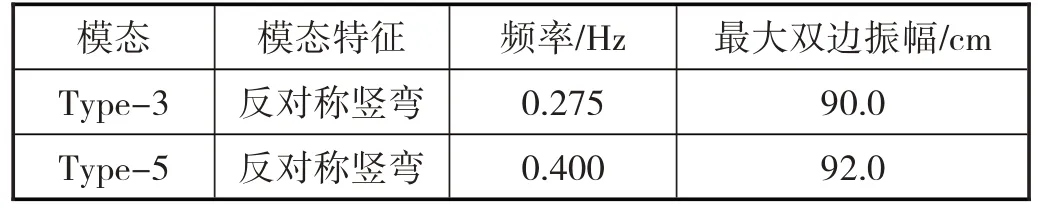
表3 反对称竖弯模态涡激共振振幅
2.3.2 宜昌至喜长江大桥的多阶模态涡激共振评估
至喜长江大桥主跨838m,采用开口钢混叠合梁,梁宽33m、高2.8m。大比例尺1/25 的阶段模型试验,进行气动措施性能研究,不加气动措施前,它的涡激共振振幅超过了规范的限制。
按悬索桥模态特征,利用一阶模态试验结果推算其他模态的涡激共振振幅。按照规范,如果换算的振幅,在各阶模态广义质量和阻尼比相等时,它的振幅基本相等,但容许值会降低。宜昌至喜长江大桥的实验结果见表4,由表4 可以看出,加劲梁成桥状态前五阶竖向涡激共振响应均满足规范要求。第6阶模态的竖向涡激共振振幅略大于限值,但其起振风速为23.9m/s,最大振幅对应的风速为25.4m/s,刚好在桥梁运营容许风速附近。
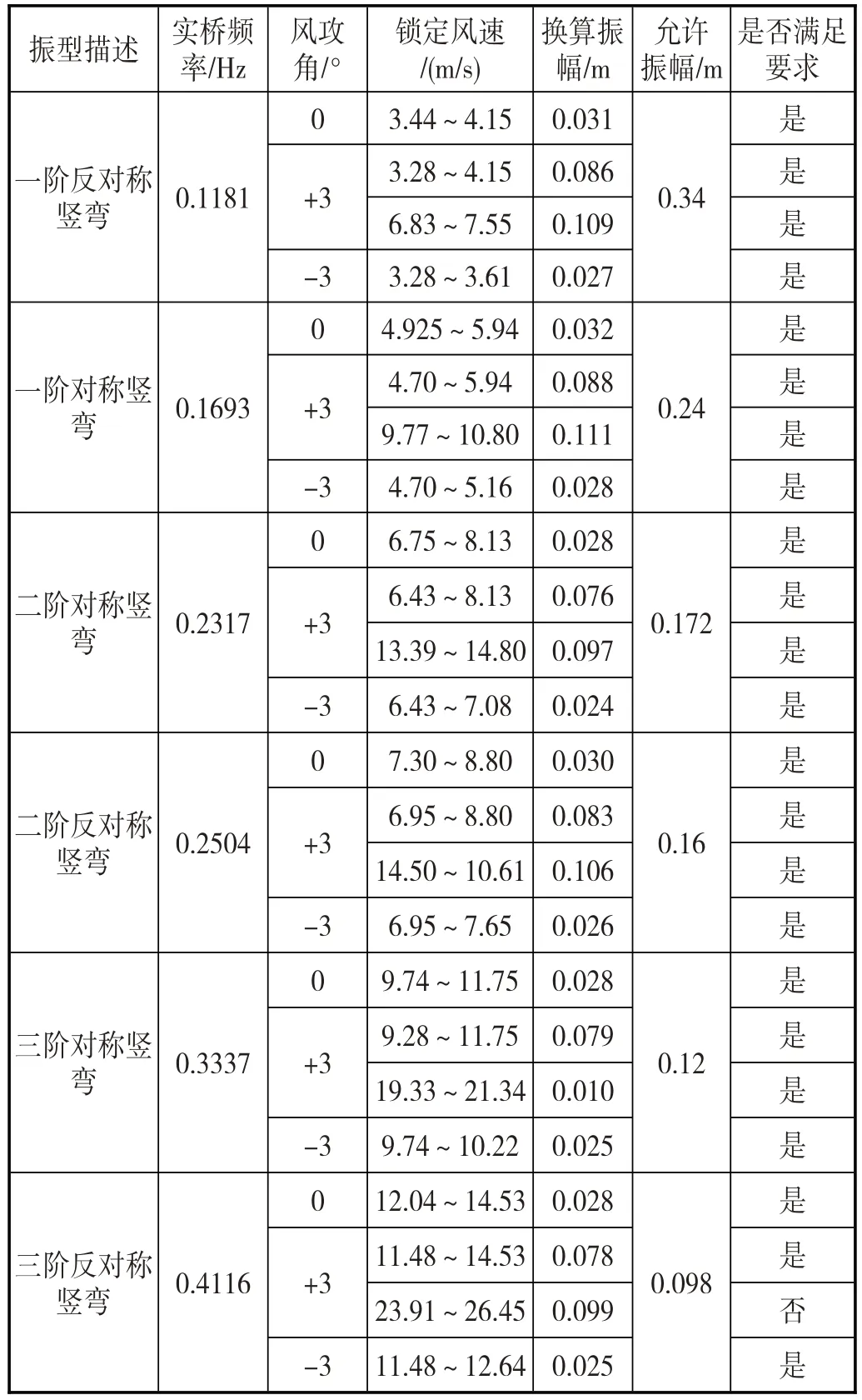
表4 宜昌至喜长江大桥多阶模态涡激共振实验结果
3 悬索桥多阶涡激共振的控制
3.1 多个模态涡激共振控制的措施
涡激共振最大振幅不仅与断面气动外形有关,还有各阶模态的振型阻尼和质量有关。因此,抑制或降低涡激共振振幅的措施包括气动措施和结构措施。其中,结构措施包括增加质量、增大刚度和提高阻尼比。
在这几种办法中,增加质量的做法在实际工程中很难实现,作用有限;而增大刚度则没有解决根本问题,尤其是对于大跨度悬索桥。
悬索桥发生涡激共振的一个主要原因就是阻尼比很小。因此,有效提高阻尼比,则是一个非常有效的涡激共振控制措施。
3.2 风致振动控制的气动措施
风致振动与结构外形有关,因此可以针对不同的断面类型进行气动性能优化,采用气动性能优良的拟流线型断面,或者附加各种可以提升桥梁抗风性能的部件,如图7 所示,这些措施的优化目标需兼顾颤振与涡激共振性能[6]。
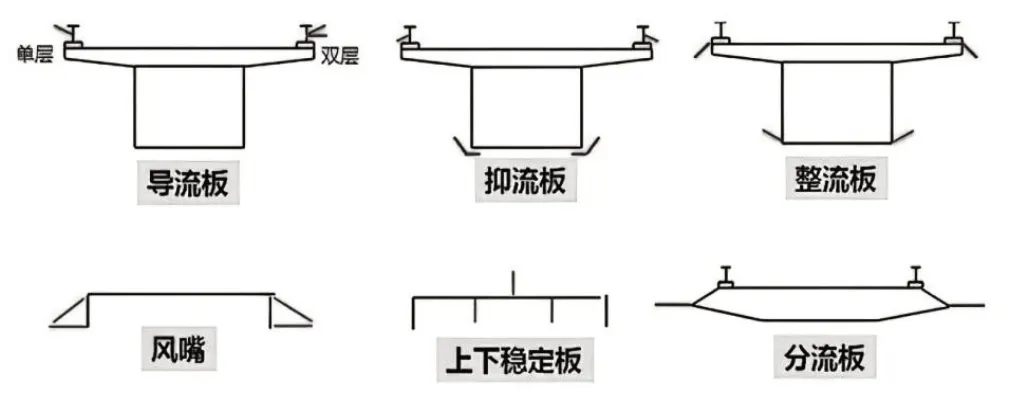
图7 提升桥梁抗风性能的部件
3.3 风致振动控制的阻尼措施
悬索桥固有阻尼很小,因此容易出现涡激共振,而且阻尼比随模态频率升高而降低,如图8 所示。我国某大型桥梁识别到的阻尼比各阶模态参数见表5,针对如此小的结构阻尼比,如果增加阻尼,将会是一个抑制涡激共振非常有效的措施。
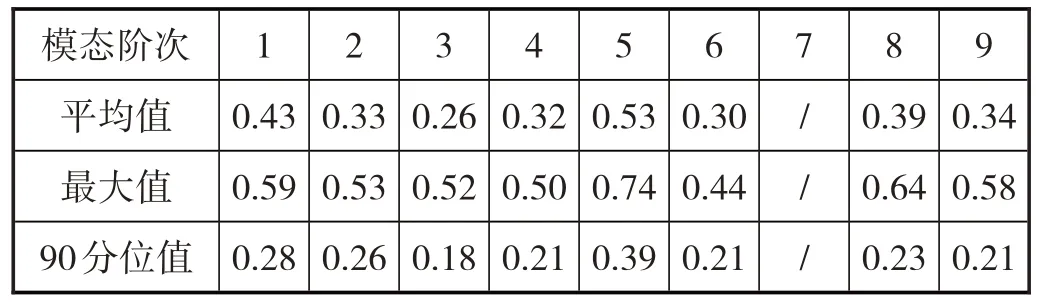
表5 我国某大型桥梁各阶模态参数
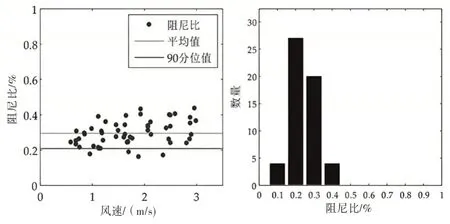
图8 我国某大型桥梁阻尼比图
4 结束语
通过以上研究,得出如下结论:
(1)大跨度钢箱梁悬索桥存在多个模态分别在不同风速下发生涡激共振的可能性,抗风研究中要检验高阶模态涡激共振;
(2)悬索桥各阶模态涡激共振振幅相等,模态加速度按频率比的平方增加;
(3)高阶模态涡激共振振幅小,因此要更加重视高阶模态涡激共振;
(4)悬索桥竖弯模态的固有阻尼低至0.2%~0.3%;
(5)对于全漂浮体系的悬索桥,塔梁之间连接阻尼器,可有效抑制多阶模态涡激共振;为实现各阶模态涡激共振的最优控制,有必要也有可能采用半主动控制。

