最小二乘法与稳健估计法在水电站大坝沉降监测数据分析中的应用效果分析

李 杰

（华北理工大学矿业工程学院，河北 唐山 064000）

0 引言

变形监测对于大坝安全状态的评估有着重要的作用，因此确保监测点的数据具有可靠性和良好的精度是非常有必要的[1-2]。但在实际的测量中，不可避免地会受到外界因素或人为因素的影响，由此产生的粗差会对整体数据的评估造成很大影响，此时再用经典最小二乘法会使实验数据的精度受到粗差的影响，使结果不可靠。而稳健估计法通过对粗差不断进行降权，具有很强的抗差性效果。因此采用稳健估计对大坝监测点的数据进行处理具有非常大的价值。

目前已有诸多学者使用稳健估计法来降低数据采集过程中产生的粗差对实验数据的影响。甄龙等[3]选用了多种稳健估计的方法对GPS中带有的粗差进行评估，得出结论：当在对独立变量进行处理时，稳健估计能得到较好的结果。陈开瑞[4]提出了稳健的总体最小二乘回归方法，对地铁监测点的沉降进行建模，结果预测精度大大提高，证明了该方法在地铁监测中使用的可行性。王刚等[5]利用稳健估计对重庆草堂隧道地表观测点进行研究，证明了稳健估计能很好地剔除误差，且Huber权函数较其他权函数有更好的抗差性。本文将运用最小二乘法和稳健估计法，在MATLAB环境中对大坝的变形监测数据在含有粗差时和不含粗差时进行处理，并对其中误差和决定系数进行对比分析，得出两种方法的优缺点及适用范围。

1 数据分析的理论模型及原理

在双江口水电站大坝变形监测中，观测数据的精度尤其重要。原始测量由于测量人的疏忽和外部环境的干扰等，测量数据里往往带有粗差[6]。如果直接对数据做平差处理，得到的结果往往不可靠。因此，为了降低粗差对整体观测数据的影响与干扰，在数据处理时调用权函数，使获得的实验结果尽可能地接近真值的有效估计。

1.1 回归分析模型

如果实验数据中存在自变量x1,x2,x3,…,xn与因变量Y，且因变量与自变量xk(k=1,2…n)有如下线性关系：

由于本次实验只涉及时间变化与大坝高程变化两个变量，因此采用的回归模型为一元线性回归模型，即：

式中：Y——大坝高程变化量；

x1——时间变化；

β0——回归方程常数项；

β1——回归系数；

ε——随机扰动项,ε~N(0,σ2)。

1.2 最小二乘法分析原理

根据测量数据与回归函数对应的拟合值，列出误差方程式：

式中：V——观测值的改正数；

B——自变量的系数矩阵；

——未知参数的近似值；

L——观测值Y的列向量。

最小二乘准则为：

1.3 稳健估计法分析原理

稳健估计可以在有粗差的条件下，尽可能大地减小粗差对实验数据的影响，得出正常模式下的最佳预测[7-8]。其基本原则就是在平差处理的过程中，通过多次迭代反复计算其权值大小，对有效数据进行充分利用，对观测数据里精度不高的数据进行降权[9]，或对含有粗差的观测数据不断进行降权直到接近于零，以消除粗差对实验数据的影响。此时可求出参数估值，此时的参数估计具有稳健性，接着可求得回归方程。设观测值的误差方程为：

限制条件为：

式中：P——观测权阵（权因子初始值都为1）；

p——密度函数。

对公式（6）求导，得Ф(Vi)=∂p/∂Vi，则有：

令权因子Wi=Ф(Vi)/Vi，等价权元素，则有则可求出：

式（5）和式（8）为第一次迭代时残差的估值和参数的估值，再通过V构造新的等价权P，并计算法方程，得第二次迭代求出的参数和残差V的估值。依照此迭代不断地进行下去，直到前后两次的差值满足限差[10]。此时可依此求出参数的第k次迭代的估值为：

2 监测数据来源与分析

2.1 监测数据来源

研究使用了该大坝在2018 年6 月至2020 年5 月每月中旬的数据，监测点观测数据如下表1所示。

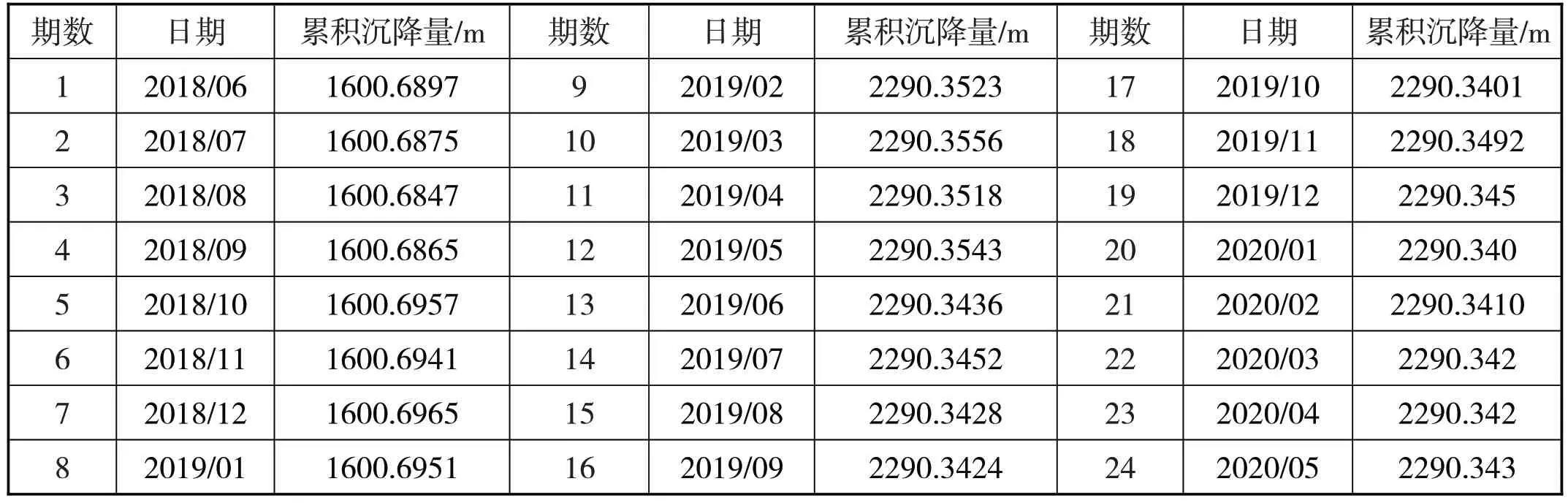
表1 大坝监测点原始观测数据统计表

由于原始数据的变化主要在毫米级上，以2018年6月1 号的原始数据高程（Z=2290.3507m）为最初点的数据，将其余原始数据处理为保留到毫米级的水库点的累积变形量，如表2所示。

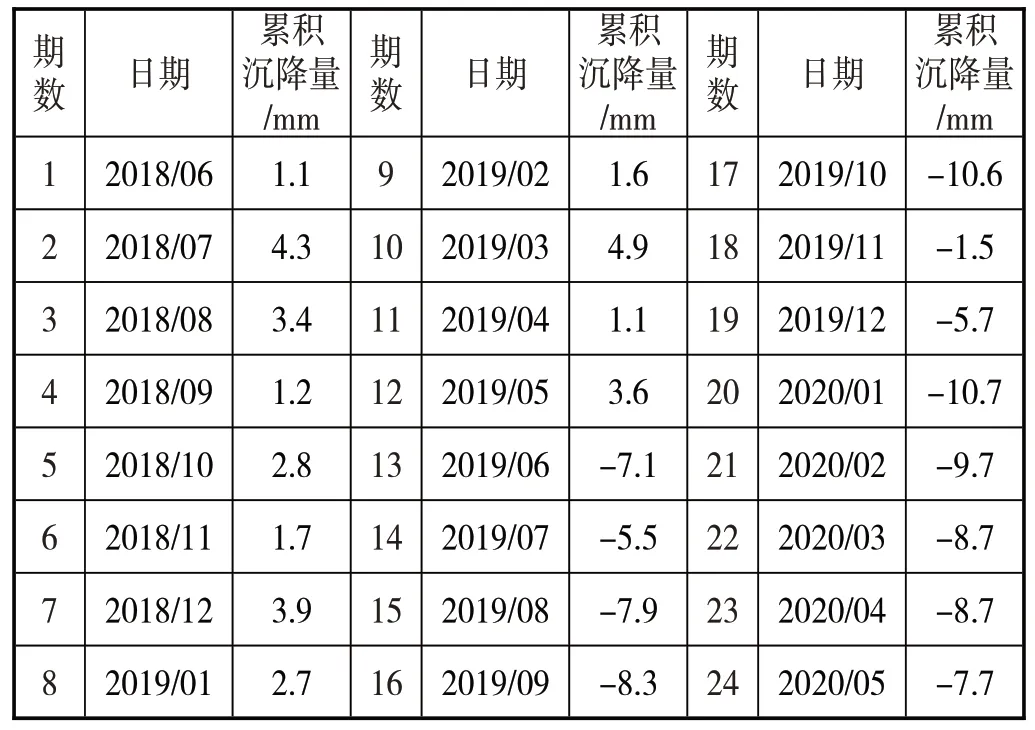
表2 处理为毫米级的累计沉降量统计表

2.2 监测数据分析

将原始各时期累积沉降量数据Z代入MATLAB 软件中，对Z变化量进行离散值的检验，结果如图1所示。

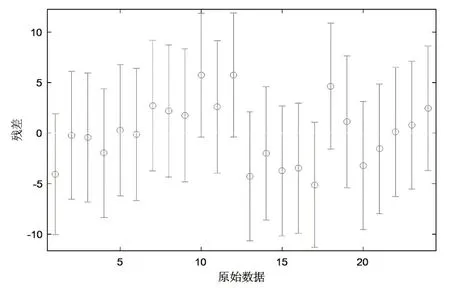
图1 原始数据累积沉降量残差图

从图1可以看出，原始数据中没有离散值，说明原始数据是可靠的。接着，分别使用最小二乘回归法与稳健估计法对原始采样数据进行建模，得出各方法的回归曲线，如图2所示。

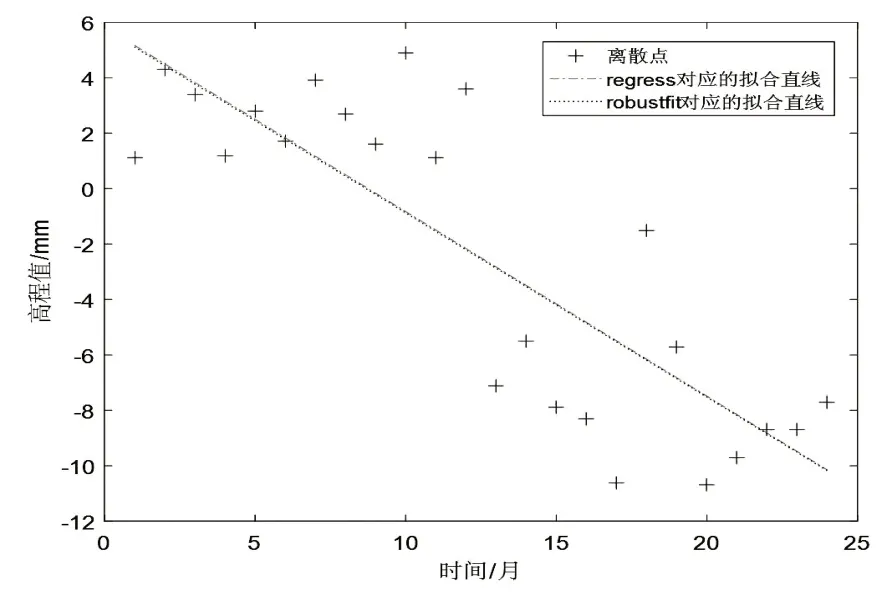
图2 原始数据累积沉降量回归曲线

此时最小二乘线性回归方程为：y=5.8355-0.6662x；中误差σ1=3.2024；R2=0.6934；稳健估计回归方程为：y=5.7743-0.6648x；中误差σ2=3.4279；R2=0.7653；由以上实验结果可知，在没有粗差时，最小二乘法和稳健估计法的结果非常接近。

接着在第22期数据中对累积沉降量Z中加入粗差，对带有粗差时的累积沉降量数据的进行分析，如图3所示。从图3中可知第22期数据为粗差，会对整体数据精度造成影响，需要被剔除。带粗差数据累积沉降量回归曲线如图4所示。

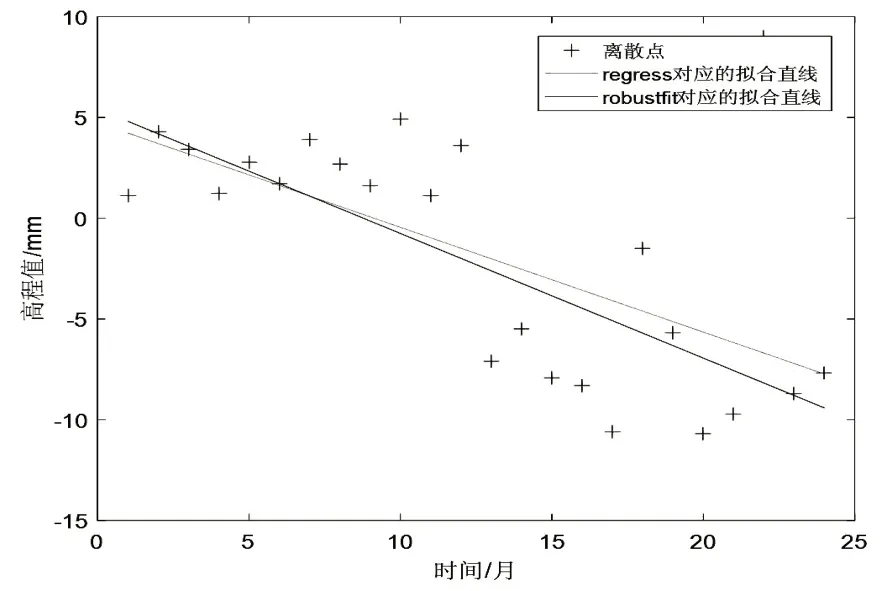
图4 带粗差数据累积沉降量回归曲线

从图4中可以看出，此时最小二乘线性回归方程为：y=4.7453-0.52x，其中误差σ1=4.7936，R2=0.3808；稳健估计回归方程为：y=5.4264-0.62x，其中误差σ2=3.9471，R2=0.7562。

通过以上数据结果分析可知，对处理有粗差的数据，稳健估计的中误差明显更小，且它的R2也明显优于最小二乘线性回归，与没有粗差时的值接近。说明稳健估计已自动对粗差进行了降权，使得粗差对整体数据的影响较小，也就是稳健估计具有良好的抗差性。

3 结束语

通过对比原始数据与加入粗差后的数据可以看出，当原始数据集中没有粗差时，最小二乘法与稳健估计法的中误差和方程都比较相似；当原始数据集中有粗差后，使用经典最小二乘回归拟合出来的结果明显偏向粗差，偏离真实值。而带有粗差的数据集中，稳健估计能通过对粗差降权，使粗差对整体数据集的影响降低，它有更小的中误差和更高的精度表现。总之，采用经典最小二乘法和稳健估计法的计算结果表明，稳健估计法具有良好的抗差性作用。