内波作用下水下航行体应急上浮的运动及水动力数值模拟研究
黄苗苗,张 楠,李迎华,王文涛
(中国船舶科学研究中心水动力学重点实验室,江苏 无锡 214082)
0 引 言
海洋内波是发生在密度稳定层化的海水内部的一种波动,是世界各大洋尤其是边缘海中一种普遍的海洋现象,其最大振幅出现在海水内部[1]。相对于海水与空气接触的自由面上下密度差来说,内波跃层的密度差很小,相当于将分层介质置于微重力场中,所以恢复力也更小,仅为水面波的0.1%量级[2]。因此在能量相同的条件下内波波幅可以是水面波的20~30倍。海洋内波特别是强流速、大波幅的内孤立波对海洋结构物具有极大的破坏性。
在海洋内波对水下航行体的水动力影响方面,国内开展了一定研究[3-7]。试验及计算结果均表明,遭遇海洋内波会引起水动力突变,由此影响水下航行体的安全航行。对于水下航行体来讲,在危急情况比如舵卡、损失浮力和危险纵倾时,可采用高压气吹除主压载水舱的方式实现应急上浮,这也是水下航行体抗沉的重要措施[8]。水下航行体遭遇内波,必要时亦可采用这种方式脱险,但是这方面的研究较少。
目前,水下航行体运动模型形式较多,其中美国的葛特勒方程最具权威性。由于水动力系数项较多且求解困难,目前研究应急上浮运动大多数使用应急上浮简化运动模型,其中使用较多的是垂直面运动方程,其他附加力的计算模型主要采用经验公式来求解[9-10]。随着近几年CFD 技术及计算机硬件的快速发展,越来越多的学者开始采用数值计算方法来研究水动力与运动问题。美国的Carrica等[11-12]基于自主研发的流体软件CFDShip-Iowa,实现了不同工况下航行体六自由度运动的数值模拟计算,并对其操纵性进行了预报;Bettle[13-14]等和Watt等[15]用六自由度求解器数值模拟并分析了水下航行体上浮过程的运动特性;国内周广礼等[16]和闫朋[17]采用粘流方法开展了静水中的应急上浮运动研究,为解决复杂环境下的应急上浮问题打下了良好基础。
在前期开展的内波对水下航行体水动力、运动特征的影响研究[6,18]的基础上,本文考虑海洋内波的非定常影响,开展内波环境下的应急上浮运动数值模拟研究,针对无航速水下航行体模拟实施高压气吹除主压载水舱的上浮运动,并对上浮过程中的运动特征开展详细分析。本研究可为后续内波下有航速的水下航行体主动操控研究打下基础。
1 数值计算方法
1.1 控制方程
本文数值计算采用的控制方程包括连续性方程及动量方程,湍流模式选取Realizablek-ε模型。
连续性方程:
动量方程:
式中,ρ为密度,P为压力,τxx、τxy和τxz等是因分子粘性而产生的作用在微元体表面的粘性应力τ的分量,Fx、Fy和Fz是微元体上的体积力分量。
依据牛顿第二定律,应用质心运动定理和相对于质心的动量矩定理,水下航行体的六自由度运动方程表达为
式中,F与M分别为航行体所受外力及外力矩,B=(mu,mv,mw)为动量,K=(Ixp,Iyq,Izr)动量矩,U=(u,v,w)为速度,Ω=(p,q,r)为角速度。
内波对于水下航行体运动的影响主要表现在垂直面上。因此,本文数值模拟中采用了三自由度运动控制方程,具体为
1.2 数值造波理论
本文采用造波边界条件进行内孤立波的数值造波,通过波的解析解或数值解在边界上给定一个波动速度作为边界条件,以实现造波。根据内孤立波的定义可知,海洋内波产生的根源是海水密度分层,因此不管是物理试验还是数值模拟,造波必然是在分层流中进行的。根据海洋学中著名的“刚盖假设”[2],将海水表面视为刚性平面,内波简化为两层流问题。本文根据KdV 理论[19]开展数值造波,内孤立波的波面表达式为
式中,a为波幅,λ为内孤立波的特征波长,c为内孤立波的传播速度,x为坐标值,t为时间。
1.3 计算模型及网格划分
本文研究对象为国际通用的SUBOFF标模,主尺度见表1。
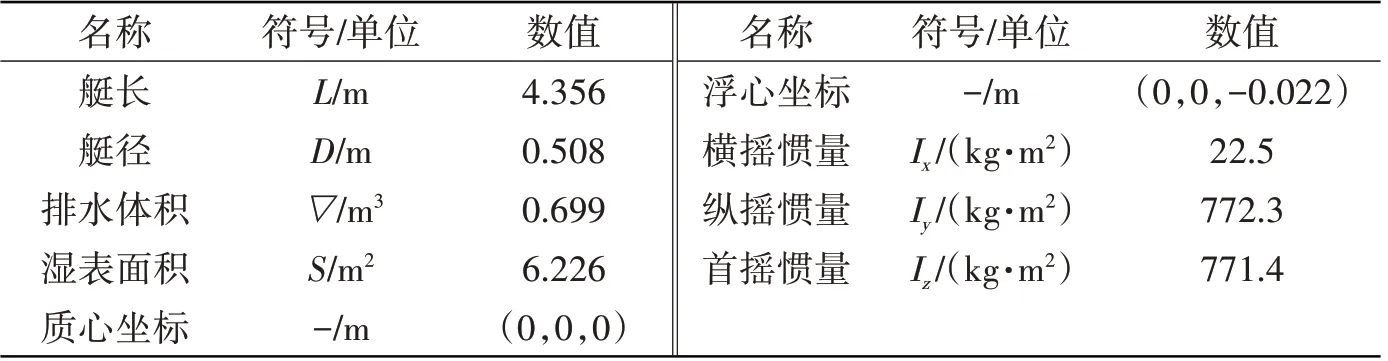
表1 SUBOFF标模主要参数Tab.1 Main parameters of SUBOFF model
开展内波对于水下航行体影响研究的前提是建立内孤立波的数值造波水池。如图1 所示,计算选用的数值造波水池总长为1000 m,上层水深为40 m,下层水深为175 m,上下两层流体的密度比ρ1/ρ2=0.993,波幅a=5.0 m。计算中大地坐标系为E-XYZ,X轴正方向指向内孤立波前进方向,Z轴正方向垂直指向上方,Y轴正方向满足右手法则。另外,为了在数值模拟中计算水下航行体的自身运动,建立随水下航行体运动的动坐标系G-xyz。该坐标系满足右手法则,原点取在水下航行体的质心处,x轴正方向指向航行体首部,y轴正方向指向右舷。

图1 坐标系的定义Fig.1 Definition of the coordinate systems
采用重叠网格方法处理运动计算过程中的网格问题。重叠网格方法将复杂的流动区域分成几何边界比较简单的子区域,流场信息通过插值在重叠区边界进行匹配和耦合。本文计算域包括两套网格:背景网格和水下航行体网格。背景网格计算域的边界条件设置如图2 所示,具体包括:速度入口造波;压力出口;水池顶部根据海水自由表面刚性假定设为壁面;水池底部也设置为壁面。
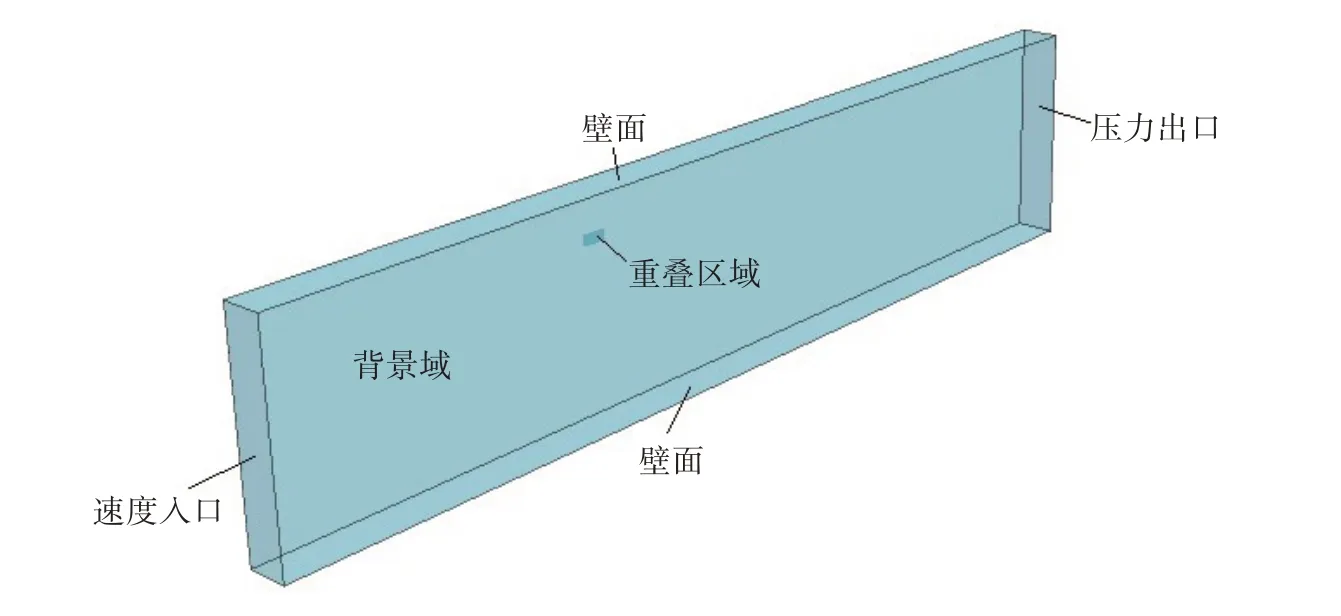
图2 计算域和边界条件Fig.2 Computational model and boundary conditions
在计算域中生成六面体网格,对航行体模型表面附近网格加密,其中第一层网格间距根据y+确定(y+范围为40~100)。为更好地捕捉波面,网格划分时对内孤立波通过的区域进行了网格加密。此外,为准确地模拟水下航行体的水动力及流场特征,对模型主附体周围的网格进行细化处理,艇体表面及近壁区域的网格划分如图3 所示。本文计算模型网格总数为805 万,其中数值水池背景网格为405万,水下航行体区域网格为400万。

图3 SUBOFF模型附近的网格划分Fig.3 Meshes around SUBOFF model
2 数值计算方法验证
为了验证应急上浮运动的数值计算方法,本文开展了水下航行体应急上浮运动数值模拟,并与相同工况的水池模型试验对比。该试验在中国船舶科学研究中心的露天水池开展,通过调整模型的配重,使模型处于静均衡状态。初始时刻水下航行体位于水深7 m 的位置,初始航速为0。试验状态为静水中抛载自由上浮,抛载量为排水量的1.48%。
水下航行体的潜深变化实时监测对比如图4所示,其中实线为水池试验结果,虚线为数值计算结果。抛载之后航行体的潜深在初期变化较小,后期随着速度的增加,潜深快速减小,直至接近水面。这符合物体从静止状态在外力作用下加速度运动的物理现象。图5是水下航行体上浮过程中纵倾角变化的对比曲线,上浮过程中抬首角度先是增大,之后变小,并快速转变为一定程度的埋首。对比可见,应急上浮运动的数值模拟结果与试验结果一致,也说明本文建立的水下航行体应急上浮运动数值计算方法是可靠的。

图4 潜深变化对比曲线Fig.4 Comparison of depth change curves
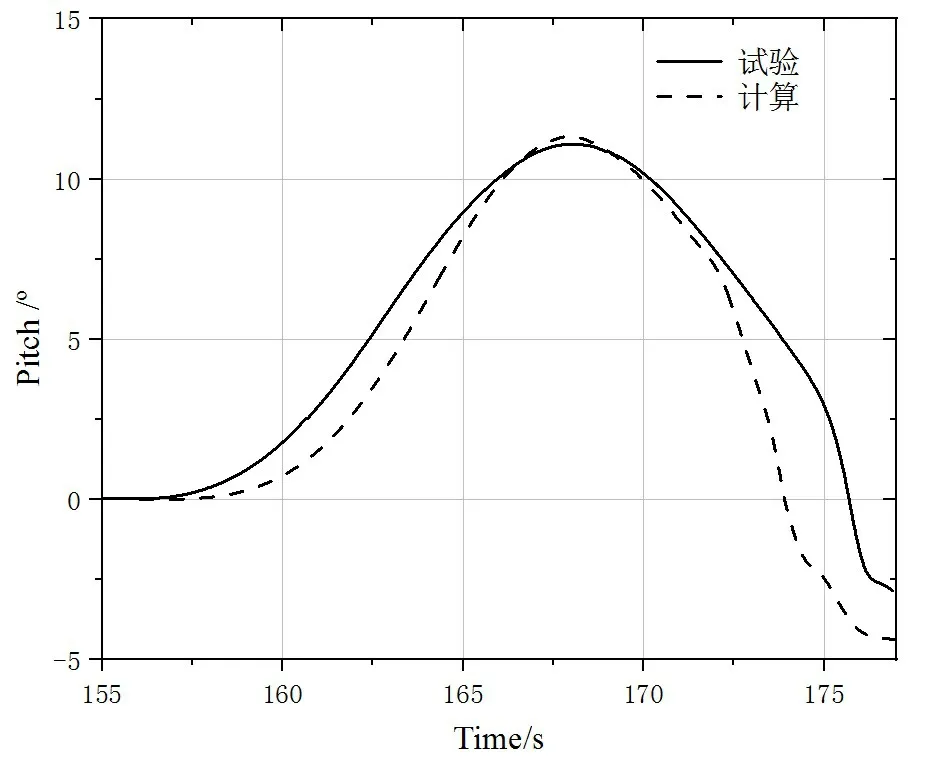
图5 俯仰角变化对比曲线Fig.5 Comparison of pitch angle history curves
3 数值结果分析
3.1 自由运动
水下航行体初始位置位于分层流的下方水体,相对于波幅0.4 倍深度的位置,初始时刻水下航行体自身重力与浮力相等,航行体水平放置首部迎流、0 航速。在波形稳定了之后水下航行体开始自由运动。
内波作用下,水下航行体的自由运动模拟结果如下述所示。图6 是航行体运动过程中水平位移(Δx)及垂向位移(Δz)的时历曲线。从中可以看出,遭遇内孤立波后,水下航行体迅速下沉并被拖向内波波谷方向,自由运动75 s 之后垂向位移已接近一倍航行体长度。说明水下航行体遭遇大幅内波,若不采取主动操控,潜深会大幅度变化,并很可能到达危险深度。

图6 模型位移变化时历曲线Fig.6 Displacement histories of the model
初始运动时刻水下航行体周围的速度场如图7 所示。整体来看,航行体周围流场的水平速度指向左方,航行体垂直速度指向下方。在这种速度场的作用下,水下航行体自由运动时自然朝左下方移动,也就是下沉并被卷拖进内波波谷中心。这里需要说明的是:在图7(b)局部放大图中,水下航行体近体下方的垂向速度场与其他区域不同,这主要是由于航行体受到来自上方的强烈速度场作用,在其近体下方形成了典型的背风区特征。可以说内波的出现改变了水下航行体周围的速度场,速度场的改变引起了水下航行体表面压力的变化,从而导致其运动的改变。
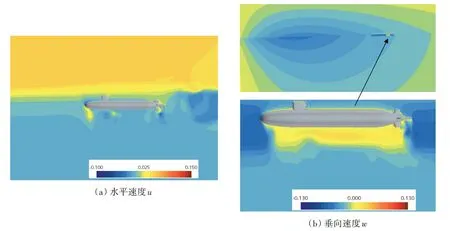
图7 初始运动时刻的速度场云图Fig.7 Velocity distributions at start moving moment
图8 是水下航行体运动过程中自身俯仰角度的变化曲线。图9 是运动过程中水下航行体受到内波水动力作用产生的俯仰力矩时历曲线,力矩作用中心为航行体质心位置,其中无量纲俯仰力矩系数为,My为俯仰力矩。My正值代表抬首力矩,负值为埋首力矩。整体来看,在185 s左右其遭受的埋首力矩明显大于抬首力矩,所以这时俯仰角度快速增大(埋首);之后俯仰力矩逐渐变为正值,205 s附近抬首力矩占主导,因此航行体埋首角度快速减小;之后俯仰力矩又变为负值,所以在220 s开始又出现了埋首加剧现象,并在之后出现轻度反复。可见水下航行体的姿态与俯仰力矩密切相连。水下航行体除了受内波流场水动力的作用外,还受到自身恢复力矩的作用,在两者同时作用下,水下航行体不断运动从而寻求平衡,这是一个典型的水动力与运动相互耦合的作用过程。

图8 模型俯仰角时历曲线Fig.8 Pitch angle history of the model

图9 俯仰力矩系数时历曲线Fig.9 History curve of pitch moment coefficient
另外值得注意的是,图9 中水下航行体在运动过程中俯仰力矩的时历振荡十分显著。为了研究其振荡特性,对该时域数据开展傅立叶变换,获得功率谱密度(power spectral density,PSD)分布,结果如图10 所示。功率谱密度较大的几个点对应的频率分别是0.034 Hz、0.026 Hz 和1.05 Hz。这说明水下航行体在遭遇内波后属于低频运动变化,是一个非稳态的过程,图9力矩曲线的振荡特征是正常的。

图10 俯仰力矩系数的功率谱密度Fig.10 Power spectral density of pitch moment coefficient
3.2 应急上浮
由上一节的模拟结果可知,在内波速度场的卷带作用下,水下航行体向着内波波谷中心快速下沉。如图11 所示,图中曲线为内波的波面,此时水下航行体垂向位移Δz/L>0.8。针对该情况,实施水下航行体的应急上浮。数值计算中采用施加可变外力的方式来模拟高压气吹除主压载水舱,吹除时间按照斯特罗哈尔数相似原则计算给定。

图11 上浮时刻水下航行体周围的流场Fig.11 Flow field around submarine at the moment to float
图12~14 中虚线对应的时间t=225 s,即开始实施应急上浮的时刻。图12 是实施应急上浮措施前后的水下航行体位移变化曲线。可以看出,在实施应急上浮之后,由于惯性作用,水下航行体继续下沉了一段距离,但很快垂向位移与水平位移曲线都出现了拐点变化,垂直方向由下沉转变为快速上浮,水平方向表现为水下航行体的前移速度趋缓。总体来看,实施应急上浮措施之后,水下航行体朝着偏离内波波谷的方向发展。

图12 模型应急上浮垂向及水平位移时历曲线Fig.12 Vertical and horizontal displacement curves of floating submarine
图13 是应急上浮过程的水下航行体俯仰角度的时历曲线。可以看到自由运动阶段一直保持埋首姿态下沉的水下航行体,在实施应急上浮之后,俯仰角快速转为抬首,在t=238 s 时抬首角度达到最大,之后变小并转为埋首。

图13 应急上浮俯仰角变化曲线Fig.13 Pitch angle history of SUBOFF emergency floating
图14 是航行体垂向速度监测曲线,下沉为负,上升为正。从中可以看到,在实施应急上浮措施之后,垂向速度由负值逐渐拉升为正值。值得注意的是,垂向速度在t=238 s时达到最大值,之后逐渐变小。
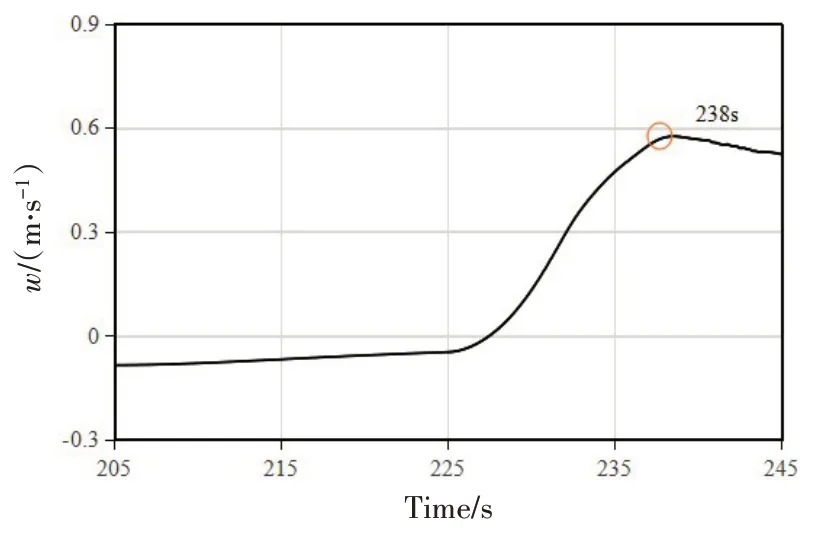
图14 应急上浮垂向运动速度时历曲线Fig.14 Time history of vertical velocity
图15(a)~(d)是上浮过程中水下航行体周围的速度场及内波的波形变化。图15(a)是实施应急上浮的初始时刻,水下航行体周围速度场主要受内波的影响,波面上方速度较大,波面下方速度较小;从图15(b)~(c)可以明显看出在实施应急上浮操纵之后,水下航行体开始抬首、上浮,航行体下方附近的海水由于粘带作用速度也越来越大;图15(d)表示水下航行体穿越波面之后,抬首角度变小,之后转为埋首。

图15 应急上浮过程中的速度场云图Fig.15 Velocity distributions around floating submarine
图16 是航行体上浮过程中的波形变化云图,波面上方是低密度海水,波面下方是高密度海水为平均密度,ρ'=。从中可以看到航行体与内波波面的变化,在这个过程中水下航行体逐步上浮、接近内波波面并最终穿越波面。总的来讲,水下航行体上浮穿越内波波面的运动特征与水下航行体的应急上浮出水现象相似。

图16 应急上浮过程中的水下航行体和波形变化Fig.16 Model and internal waves in the process of floating up
为了探究水下航行体在内波中应急上浮运动特征的形成原因,本文进一步开展了理论分析。图17是航行体穿越内波波面前后的受力分析示意图,其中G为重力、F为浮力。当航行体以抬首姿态冲出波面时,在波面上下海水密度差的影响下,浮力变小并且作用点后移,而重力的大小及位置不变,于是形成了一对较强的逆时针作用力矩。在这对力矩的作用下,水下航行体冲出内波波面之后抬首角度迅速变小并开始转向埋首姿态。这就是前面数值模拟中航行体俯仰角及上浮速度时历曲线在238 s时出现拐点变化的原因。

图17 受力分析示意图Fig.17 Forces diagram of submarine
4 结 论
本文采用RANS 方法结合运动控制方程,开展了海洋内波作用下的水下航行体运动特征数值计算研究,其中静水中的应急上浮运动与模型试验吻合,证明了计算方法切实可行,主要结论如下:
(1)数值计算表明,处于分层流下方的水下航行体在遭遇内波之后,即使未穿越波面,也会由于速度场的改变导致航行体表面压力的改变,从而出现埋首下沉现象。这个过程中,水下航行体除了受内波流场水动力的作用外,还受到自身恢复力矩的作用,在两者同时作用下水下航行体不断运动从而寻求平衡,这是一个典型的水动力与运动相互耦合的作用过程。
(2)在此研究基础上,文中采用数值计算方法模拟了高压气吹除主压载水舱的作用,针对水下航行体遭遇内波迅速下沉的情况,开展了应急上浮运动的数值模拟。结果表明,实施紧急操控之后,水下航行体能够快速改变运动轨迹、由下沉转变为上浮并脱离内波影响;上浮后期,航行体以抬首姿态快速冲出波面之后转为埋首。文中对上浮运动特征开展了详细的分析,数值模拟结果与理论分析一致。

