基于Midas的h型抗滑桩数值模拟研究

罗登品

(广西河池市公路事业发展中心,广西 河池 547099)

0 引言

近年来,随着我国基础设施的大规模建设,边坡治理工程增多。h型抗滑桩因具有自身结构刚度大、抵抗滑坡推力能力强、治理边坡效果显著等优点,在边坡治理中得到广泛应用。为此,众多学者们对h型抗滑桩进行了大量的研究。管永伟[1]利用数值模拟技术,对h型抗滑桩治理边坡工程进行了研究,结果表明:h型抗滑桩前后排桩在结构上具有较好的协同作用,且数值模拟结果与实际工程效果相近。王晨涛等[2]利用理论分析与现场监测相结合的方法,对h型抗滑桩的分析方法及其在边坡治理中的应用进行了研究,结果表明:提出的理论分析方法与实测值基本吻合,且边坡经h型抗滑桩支护后,边坡位移显著减小。顾博凯[3]利用Midas GTS软件,对h型抗滑桩支护开挖边坡进行了数值模拟研究,结果表明:经h型抗滑桩支护后,边坡的位移均在合理的范围内,边坡稳定性显著提升。刘松等[4]利用数值模拟技术,建立h型抗滑桩支护边坡模型,对h型抗滑桩的内力与坡体治理效果进行了研究,结果表明:h型抗滑桩在治理坡面不能防护的边坡时,治理效果显著。赵玉博等[5]利用FLAC 3D软件,分别对单桩与h型抗滑桩的滑坡治理效果进行了研究,结果表明:与单桩相比,h型抗滑桩在限制坡体位移方面表现更显著,滑坡治理效果更佳。何志俊[6]利用数值模拟技术,对h型抗滑桩优化设计进行了研究,结果表明:臂段长度及锚固深度的合理尺寸分别为15 m和13 m。

以上研究从多个方面对h型抗滑桩进行了深入分析,然而只是针对h型抗滑桩某些特征的研究,如只针对桩身位移或只针对限制边坡位移等。关于h型抗滑桩完整数值模拟的研究,应包含h型抗滑桩的桩身位移、桩身内力以及边坡治理效果的分析。基于此,本文结合广西南宁市某具体公路边坡治理工程,利用Midas软件,建立h型抗滑桩治理边坡模型,对h型抗滑桩的桩身位移、桩身内力以及边坡治理效果进行数值模拟研究,研究成果可为治理类似边坡时h型抗滑桩的选用提供参考。

1 工程概况

该公路边坡工程位于广西南宁市,边坡地形地貌为构造侵蚀-剥蚀中低山,自然坡度为20°～35°。坡顶植被较为发育,以灌木为主,夹杂少量草、小乔木。边坡上部土层为风化土,分布于坡体及坡顶表层,黄褐色-红褐色,可塑状,层厚度为4～17 m;中部为风化岩,全场地分布,灰黄色-青灰色,岩石组织结构大部分破坏,矿物成分显著变化,岩芯多呈碎块,页理十分发育,层厚度为21～45 m,矿物成分显著变化,但仍能分辨其原始结构;风化土与风化岩局部接触区域有软弱夹层,夹层为黑色,层状、薄层状构造,由炭质及泥质构成,含碳量高,质地极软,钻进快,最大层厚为8.5 m;下部为软岩,全场地分布,青灰色,细粒结构,薄层状构造,丝绢光泽,主要由泥质、钙质组成,可见少量方解石细脉,页理清晰,节理、裂隙较发育,岩芯多呈短柱状、饼状。经现场勘测与滑坡推力计算分析得,该滑坡为大推力滑坡,工程人员决定采用正放h型抗滑桩进行治理。正放h型抗滑桩设置在坡脚附近,且后排桩桩身紧靠软弱夹层右边界,边坡最危险截面如图1所示。

图1 边坡最危险截面图

h型抗滑桩混凝土强度等级为C30,抗滑桩前排桩桩长为20 m、后排桩桩长为28 m,桩身截面尺寸与连梁截面尺寸均为2 m×3 m,连梁长度为6 m。抗滑桩前后排桩桩底水平高度相同,连梁水平,连梁左端与前排桩桩顶连接,连梁右端与后排桩埋深8 m位置处连接,h型抗滑桩与岩土体物理力学参数如表1所示。

表1 h型抗滑桩与岩土体物理力学参数表

2 有限元模型的建立

本文采用Midas GTS软件,建立h型抗滑桩支护边坡模型。其中,边坡岩土体材料选用摩尔-库仑(Mohr-Coulomb)本构模型,按2D平面应变考虑;h型抗滑桩材料选用线弹性本构模型,按1D植入式梁单元考虑。模型左边界高为93 m,长度为171 m,右边界高为38 m。为保证计算结果的准确性,模型以单元尺寸为2 m进行网格划分。考虑到抗滑桩与岩土体不同属性单元之间接触的受力均匀问题,在抗滑桩与岩土体接触处共用单元节点。抗滑桩连梁与前后排桩的连接均为刚性连接,能够保证同时传递弯矩与剪力。有限元模型如图2所示。

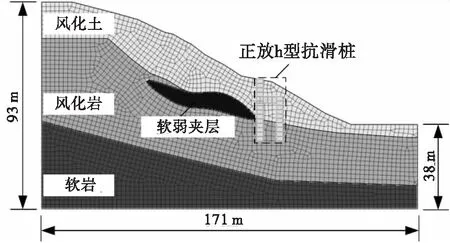
图2 有限元模型图

3 数值模拟结果分析

通过有限元软件运算求解,得出h型抗滑桩的桩身位移、桩身弯矩、桩身剪力、桩身轴力、边坡治理效果,并依次对各种结果进行分析。

3.1 h型抗滑桩桩身位移分析

h型抗滑桩的桩身位移图如图3所示。由图3可知,h型抗滑桩桩身最大位移发生在后排桩桩顶,桩顶最大位移为4.7 cm,满足规范要求的桩顶最大位移不大于自由段的1/100且≤10 cm的要求;正放h型抗滑桩的前排桩与后排桩桩身位移均随埋深的增加而减小,且后排桩在连梁连接位置处,桩身位移显著减小;埋深在连梁位置以下时,h型抗滑桩的前排桩与后排桩桩身位移基本相同;由于轴向变形很小,连梁各位置的位移基本相同,位移为3.2 cm附近;在各自锚固深度处,正放h型抗滑桩的前排桩与后排桩的桩身位移均较小,这与锚固段岩层的岩土体性质相关。

图3 正放h型抗滑桩的桩身位移云图

3.2 h型抗滑桩桩身弯矩分析

h型抗滑桩的桩身弯矩图如图4所示。由图4可知,h型抗滑桩前排桩的桩身最大弯矩出现在桩顶,前排桩最大弯矩为9.6 kN·m;前排桩桩身弯矩为零的位置有一处,弯矩为0的位置距前排桩桩顶7.9 m;正放h型抗滑桩后排桩的桩身最大弯矩出现在其埋深为8 m位置处,后排桩桩身最大弯矩为4.1 kN·m;在埋深0～8 m范围内,后排桩弯矩随埋深的增加而增加;在与连梁连接位置处,后排桩桩身弯矩发生突变;后排桩桩身弯矩为0的位置有两处,两处弯矩为0的位置分别距后排桩桩顶8 m与15 m;h型抗滑桩整体的桩身最大负弯矩出现在后排桩上;深度在与连梁连接的位置下时,h型抗滑桩的前排桩与后排桩的桩身弯矩分布形式基本相同,均为类半“S”形式分布。

图4 正放h型抗滑桩的桩身弯矩云图

3.3 h型抗滑桩桩身剪力分析

h型抗滑桩的桩身剪力图如图5所示。由图5可知,h型抗滑桩前排桩的桩身最大剪力出现在其桩顶处,前排桩桩身最大剪力为1.5 kN;前排桩桩身剪力为0的位置有一处,剪力为0的位置距前排桩桩顶16 m;h型抗滑桩后排桩的桩身最大剪力出现在其埋深为18 m位置处,后排桩桩身最大剪力为1.1 kN;在与连梁连接位置处,后排桩桩身剪力发生突变;后排桩桩身剪力为0的位置有3处,剪力为0的位置分别距后排桩桩顶8 m、10 m、22 m,h型抗滑桩整体的桩身最大正剪力与桩身最大负剪力均出现在前排桩上;从整体上看,h型抗滑桩的前排桩与后排桩的桩身剪力分布形式差异明显,前排桩剪力呈现先减小、后反向增大的形式。

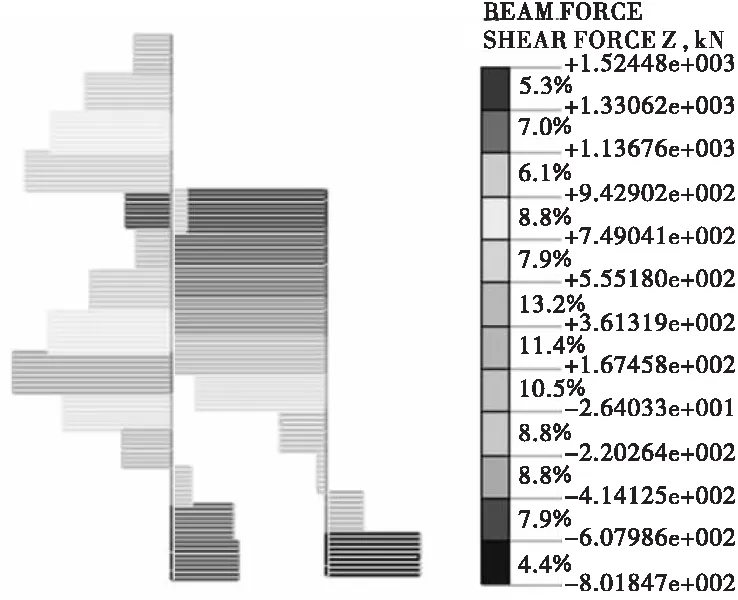
图5 h型抗滑桩的桩身剪力云图

3.4 h型抗滑桩桩身轴力分析

h型抗滑桩的桩身轴力图如图6所示。由图6可知,前排桩的桩身最大轴力出现在桩顶处,桩身最大轴力为2.6 kN;从桩顶至桩底,抗滑桩前排桩桩身始终受压,前排桩桩身轴力整体上逐渐减小;后排桩的桩身最大轴力出现在其埋深为8 m位置处,后排桩桩身最大轴力为1.9 kN;在后排桩埋深0～8 m范围内,桩身轴力很小,轴力≤0.04 kN;在与连梁连接位置处,后排桩桩身轴力发生突变,桩身由受压变为受拉;在后排桩埋深8～28 m范围内,桩身轴力整体上保持逐渐减小的趋势;在桩身锚固段范围内,正放h型抗滑桩的前排桩与后排桩的桩身轴力均明显较抗滑段更小。

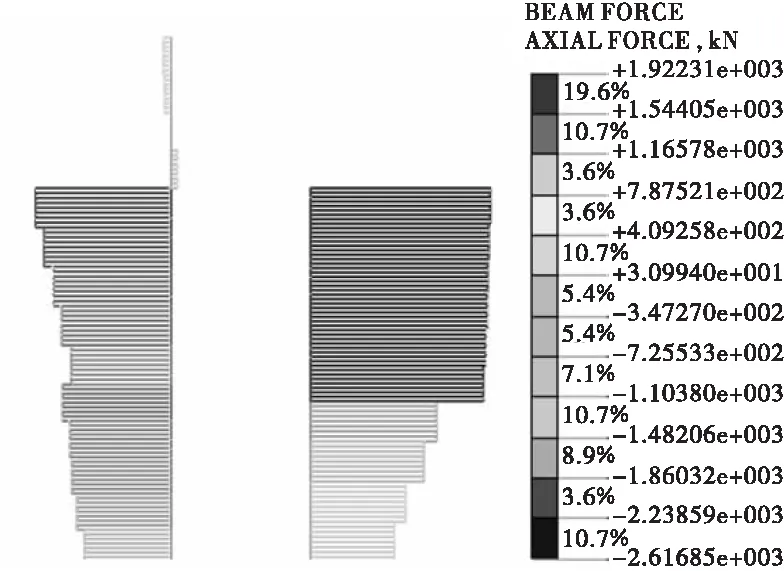
图6 h型抗滑桩的桩身轴力云图

3.5 边坡治理效果分析

天然工况下与h型抗滑桩支护工况下边坡有效塑性应变云图如图7所示。由图7(a)可知,天然工况下边坡最大有效塑性应变为0.22,最大有效塑性应变发生在软弱夹层区域;塑性应变区域主要集中于软弱夹层以及风化土与风化岩接触区域,从坡顶至坡脚,边坡有效塑性应变呈现先增大再减小的趋势。由图7(b)可知,h型抗滑桩支护工况下,边坡最大有效塑性应变为0.01,最大有效塑性应变仍发生在软弱夹层区域,有效塑性应变明显的区域较小。综合图7(a)、(b)可知,经正放h型抗滑桩支护后,边坡有效塑性区域被阻断,边坡有效塑性应变明显减小。

(a)天然工况

不同工况下边坡最大总位移与稳定安全系数如后页表2所示。由表2可知,天然工况下,边坡最大总位移达37 mm,边坡稳定安全系数仅为1.03,边坡处于极不稳定状态;h型抗滑桩支护工况下,边坡最大总位移为7 mm,较天然工况下减小了81.1%,边坡稳定安全系数为1.38,较天然工况下提升了25.4%。

表2 不同工况下边坡最大总位移与稳定安全系数表

综上所述,h型抗滑桩的桩身位移能较好地满足规范的要求;由于连梁的存在,使前后排桩能形成空间整体结构,进而使h型抗滑桩的桩身弯矩分布较为均匀;前排桩与后排桩桩身剪力分布形式基本相同;同水平高度处,h型抗滑桩前排桩桩身轴力与后排桩桩身轴力方向相反;经h型抗滑桩支护后,边坡总位移显著减小,边坡稳定安全系数显著提升,边坡治理效果较优。

4 结语

本文基于Midas GTS软件,建立h型抗滑桩治理公路边坡的模型,进而对正放h型抗滑桩的桩身位移、桩身内力以及边坡治理效果进行了全面的分析,可以得出如下结论:

(1)针对此边坡治理工程,h型抗滑桩桩顶最大位移为4.7 cm,满足规范要求。

(2)h型抗滑桩中,连梁起到协调桩身内力的作用,使桩身内力分布更加均匀,更加充分发挥前后排桩的整体抗滑作用。

(3)采用h型抗滑桩支护后,边坡总位移减小了81.1%,边坡稳定安全系数提升了25.4%,边坡治理效果显著。