结合Nyström 方法的三维网格模型分割方法
朱天晓
(上海工程技术大学电子电气工程学院, 上海 201620)
0 引 言
随着计算机视觉、三维扫描等技术的发展,三维网格模型被广泛应用于虚拟现实、影视动画等领域。三维网格模型分割是计算机图形学的重要研究点,也是互联网上模型检索、模型生成等技术的基础。三维模型精度越来越高,数据量不断增长,大大增加了分割难度。
三维网格模型分割(简称网格分割)是根据一定分割规则,将连通的网格模型分解为一组数目有限的面片集的过程。 网格分割按照不同的标准有不同的分类。 按照分割结果的不同,Rodrigues 等[1]将网格分割方法分为面片分割和部件分割,前者将网格分割成若干几何属性一致的面片集,后者将网格分割为符合人类视觉划分效果的若干部件。 按照分割方式的不同,龚思洁等[2]将现今主流的分割方法分为3 类:第一类是根据模型几何特征将模型表面具有相关性的面片合并为一类,如聚类分析法;第二类是基于最小值原则,在模型表面构建分割线,将模型拆分为多个部分;第三类是深度学习方法,通过构建深度学习网络,进行有监督学习。 深度学习方法通常对机器性能有很高的要求,此外获取优质数据集也是一个难题,因此很多研究集中在前两种方法上,计算量相对较小。 龚思洁等[2]提出能量和区分度两种模型特征用于寻找分割点,并使用腐蚀算法、最小能量原则构造分割线,得到了精度较高的分割结果,但算法耗时较长;赵云成等[3]提出了结合曲率约束的网格模型快速分割方法,根据高斯曲率和平均曲率筛选出模型的凹区域,依据最小负曲率阈值原则构造出闭合分割线,实现对网格模型的分割;这两种方法都属于基于最小值原则、构建分割线的分割方法。 对于基于聚类分析的网格分割方法,梁楚萍等[4]根据聚类过程中簇划分方式的区别,将其划分为5 类:区域生长算法、多源区域生长算法、层次聚类算法、迭代聚类算法和谱聚类算法,前4 种算法都以网格属性直接作为分类依据,而谱聚类算法核心在于对网格模型生成的亲和力矩阵的划分,该算法可以得到较高准确率。
Liu 等[5]将谱聚类引入到网格分割问题中,使用基于测地线距离和余弦距离构造的核函数计算亲和力矩阵,可以有效利用模型的几何特征进行分割,但是构建亲和力矩阵耗时较长;Jiao 等[6]在谱聚类算法框架下,使用网格显著指数和网格离散曲率构建亲和力矩阵并完成网格分割,没有解决构建亲和力矩阵时间、空间开销大的问题;万燕[7]等使用谱聚类算法将模型过分割为弱凸区域,对弱凸区域按照可见度进行排序,根据相互可见性和形状直径函数进行区域合并,最终得到分割结果,但没有解决谱聚类算法耗时长、内存消耗大的问题;Tong 等[8]对亲和力矩阵计算费德勒(Fiedler)向量,通过分析费德勒向量,将网格分割问题转化为梯度极小化问题;Li 等[9]通过分析费德勒向量、计算费德勒残差,对模型进行递归分割。仅使用费德勒向量降低了后续的计算成本,但是构建亲和力矩阵的时间、空间开销没有降低。
针对谱聚类构建亲和力矩阵耗时长、内存消耗大、难以分割面片数较多的模型的问题,本文提出了一种结合Nyström 方法的三维网格模型分割方法,能够避免构建亲和力矩阵的巨大内存开销,有效降低谱聚类算法进行网格分割所需的时间,可以获得符合人类视觉划分效果的分割结果。
1 相关技术背景
1.1 Nyström 方法
Nyström 方法是一种用于大规模数据聚类的有效方法,其最初目的是为了求解积分方程。 Williams等[10]将其引入核方法,用于加速矩阵特征分解,而准确率并没有明显下降。 近年来随着研究的深入,Nyström 方法也被用于图片分割、点云分割。
Nyström 方法适用于对称矩阵,其基本思想是通过采样获得少量样本点,使用样本点与非样本点之间的相似性来估计目标矩阵或其特征向量,采样方法有随机采样、基于K-Means 算法采样、基于最远策略采样等。
1.2 谱聚类算法
谱聚类是一种基于谱图理论的聚类算法,能在任意簇形的样本空间上达到良好的聚类效果。 该算法核心在于构建亲和力矩阵,其形式类似于图邻接矩阵。
Ng 等[11]提出了一种二维数据谱聚类算法,使用径向基函数核(Radial Basis Function kernel, RBF kernel)计算二维数据中每两点的欧氏距离,用于构建亲和力矩阵,并对亲和力矩阵的特征向量进行KMeans 聚类,实现对原始数据的聚类;Liu 等[5]在其工作基础上提出了一种谱聚类三维网格模型分割算法,将测地线距离和余弦距离引入RBF 核函数来构造亲和力矩阵,该算法在网格分割方面得到了较高的准确率。
2 本文算法流程
传统的谱聚类算法使用核函数构建亲和力矩阵,时间、空间复杂度一般为O(n2)。 对于面片数较多的模型,往往难以使用谱聚类算法对模型进行分割。
本文将Nyström 方法与谱聚类算法结合,提出了一种有效降低构建亲和力矩阵时间、空间开销的网格模型分割方法。 首先,使用K-Means++算法对模型面心进行聚类,将距离聚类中心最近的面心作为采样点;其次,使用基于测地线距离和余弦距离的核函数计算采样点和所有面心的亲和力数值,并使用Nyström 方法估计亲和力矩阵的主特征向量;将主特征向量拼接为矩阵,对矩阵每行元素使用KMeans 算法聚类,实现对模型的分割;最后,使用自适应邻域滤波算法对分割结果进行处理,得到优化后的模型分割结果。 本文方法流程如图1 所示。
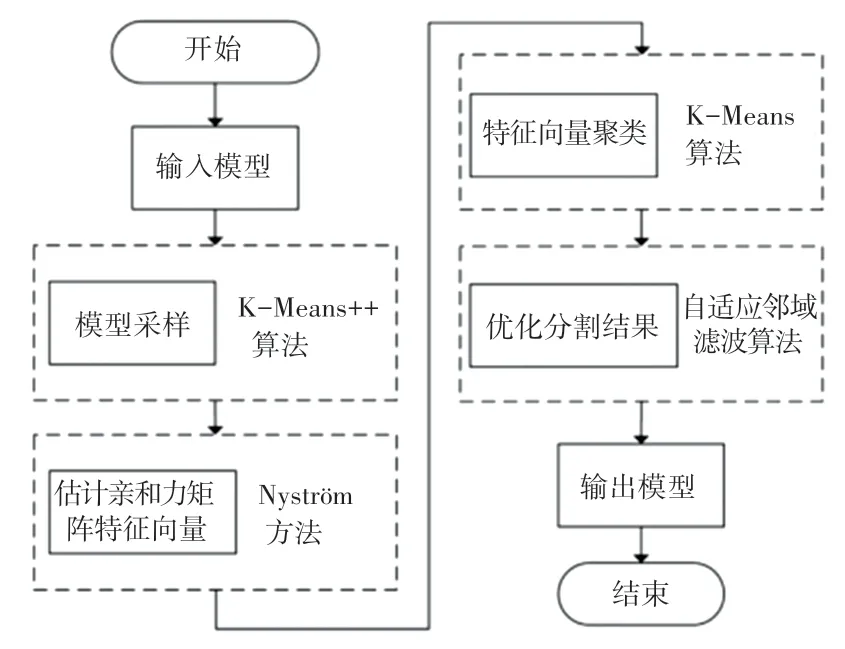
图1 本文方法流程图Fig. 1 Flow chart of the proposed method
2.1 特征向量估计
使用谱聚类算法分割模型时,若模型的面片数为N,则需要计算大小为N×N的亲和力矩阵,计算量较大、耗时较长。 因此,可以使用Nyström 方法对矩阵或其特征向量进行估计近似,提升谱聚类算法运行速度。
Oglic 等[12]证明了K -Means ++算法作为Nyström 方法中的采样方法具有可行性,并且误差较小。 K-Means++算法是K-Means 算法的改进,其初始聚类中心点的选择是基于最远策略的,即选择相互间距离尽可能远的初始聚类中心点。 本文将聚类数目设置为采样点数,对模型面片的面心进行KMeans++聚类,并选择距离聚类中心点最近的面心作为采样点。
设模型的面片数为N,从中使用K-Means++采样获得m个面心作为样本点(m≪N),则非样本点数目为n=N-m。
亲和力矩阵W可以表示为式(1):
其中,A∈,B∈,C∈,矩阵A表示采样的m个样本点之间的亲和力矩阵;矩阵B表示采样的m个样本点和剩余n个非样本点之间的亲和力矩阵;因为m≪N,所以矩阵C的大小几乎和矩阵W相同。
本文使用Nyström 方法对矩阵W的主特征向量进行估计,方法流程如图2 所示。
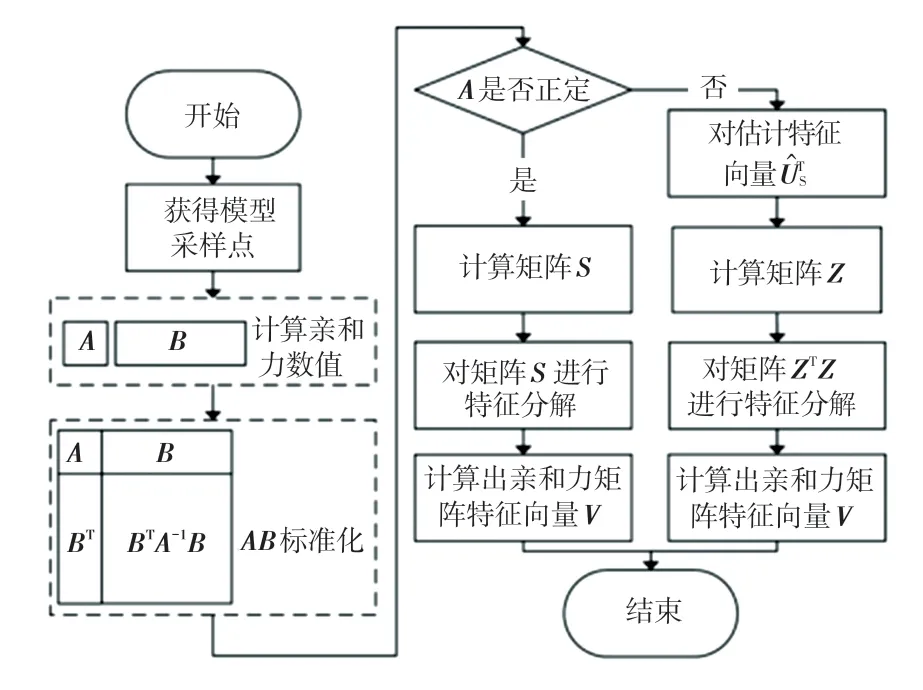
图2 Nyström 方法流程图Fig. 2 Flow chart of the Nyström method
首先,将矩阵Α特征分解,即Α=UΛ UT;Λ为对角矩阵,其中非零元素为矩阵A的特征值。 亲和力矩阵W的近似特征向量为式(2):
由式(1)、式(2)有亲和力矩阵W可近似为式(3):
由式(3)可知,矩阵C的近似值为BTA-1B。
其次,对A、B进行标准化。 因为在谱聚类算法中,使用标准化的亲和力矩阵。 对估计矩阵求行和,式(4):
其中,ar、br∈,分别表示矩阵A、B的行和;bc∈表示矩阵B的列和;1 表示元素均为1 的列向量。
使用式(4)对矩阵A和B进行归一化,式(5)和式(6):
最后,求解矩阵的主特征向量。
若矩阵A正定,令A1/2表示A的正定平方根。定义S=A+A-1/2B BTA-1/2,并将其特征分解为S=US ΛS。 可一步估算出矩阵的正交主特征向量式(7):
若矩阵A非正定,矩阵的估计特征向量为定义有Z ZT,对ZTZ特征分解,有ZTZ=FΣ FT。 最后估算出矩阵的正交主特征向量,式(8):
Nyström 方法中数据量最大的是式(3)的亲和力矩阵,但是不必真正计算该矩阵,谱聚类算法需要的是亲和力矩阵的主特征向量。 因为是由矩阵A、B计算拼接出的,而在式(4)进行标准化时,可以直接使用矩阵A、B标准化,而无需计算。
可见,最大的矩阵为,相比与传统谱聚类算法需要计算,本文使用Nyström 方法对亲和力矩阵主特征向量进行估计近似,大大降低了时间、空间开销。
2.2 网格模型分割
本文计算面片i到相邻面片j的测地线距离,式(9):
其中,li、lj分别为面片i、j的交线中点pl到对应面片质心pi、pj的欧式距离。
本文定义面片i到相邻面片j的余弦距离为式(10):
其中,ni为面片i的法向量,nj为面片j的法向量。
使用式(9)、式(10)构造的加权距离公式为式(11):
其中,n为面片数;δ为衡量测地线距离与余弦距离重要性的参数;η为调整余弦距离的参数。
本文设置δ=0.03,η=0.15。
使用式(11)构造的亲和力数值计算式(12):
本文提出的结合Nyström 方法的谱聚类算法流程如下:
(1)对面片集M={m1,…,mn},使用K-Means++算法确定m个采样点;
(2)使用式(12)计算m个采样点与自身以及与剩余n个非样本点之间的亲和力矩阵;
(3)使用Nyström 方法估计亲和力矩阵W^的m个主特征向量, 并按列排放, 组成矩阵V=[e1,e2,…,em] ;
(4)对矩阵V每行元素进行单位化,得到矩阵V′;
(5)将矩阵V′ 中每行元素视为映射到m维空间的特征点,并对其进行K-Means 聚类,聚类数目为m。
最后,如果矩阵V′的i行分配给簇j时,将原始面片mi分配给簇j。
2.3 分割误差优化
Nyström 方法获得的亲和力矩阵特征向量是近似计算得出的,因此在分割时会出现一定的误差,分割模型误差俯视图如图3 所示。

图3 分割模型误差俯视图Fig. 3 Top view of segmentation error
可见,分割误差类似于二维图像中的椒盐噪声,椒盐噪声的消除方式一般是使用中值滤波方法。
二维图像中使用像素邻域滤波,在三维网格中可以使用面片邻域进行滤波。 面片i的一阶邻域、二阶邻域如图4 所示。
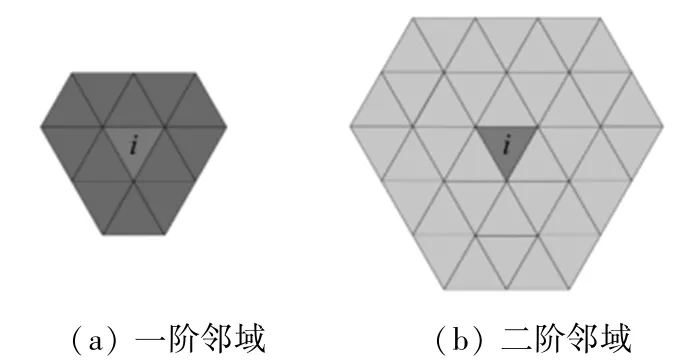
图4 面片i 邻域示意图Fig. 4 Diagram of the neighborhood of surface i
参考目前去噪效果较好的自适应中值滤波算法,本文使用面片邻域作为滤波算子对分割模型进行优化,提出了一种网格模型自适应邻域滤波算法。该算法遍历模型面片进行优化,其核心是对误差的判断。
若面片i的一阶邻域中均为同一种颜色C且与面片i颜色不同,则将面片i视为误差,并将其颜色设置为颜色C。
若面片i一阶邻域中存在两种(或以上)颜色Ca、Cb,并且数量最多的颜色Cm占比超过80%,同时面片i颜色不为Cm,则将面片i视为误差,将其颜色设置为颜色Cm。
若一阶顶点邻域中数量最多的颜色Cm占比不超过80%,同时面片i颜色不为Cm, 则将邻域扩大为二阶邻域进行判断,将面片i颜色设置为二阶邻域中数量最多的颜色。
使用自适应邻域滤波算法对分割结果进行优化,得到优化后的模型俯视图如图5 所示,基本上消除了因矩阵估计引起的分割误差。
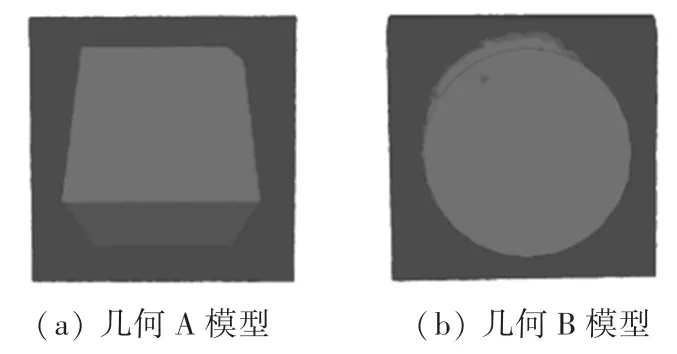
图5 分割模型优化结果俯视图Fig. 5 Top view of optimization results of segmentation
3 实 验
本文使用Python 编程实现方法,在CPU 为Intel Core i5-6300HQ(2.30 GHz)、内存为16 GB、系统为Windows 10 的PC 上进行实验。 由于普林斯顿数据集中模型面片数较少,本文从中选择了8 类,每类2 个,共计16 个网格模型进行Loop 细分,并进行人工二分割,作为实验数据集。
使用Nyström 方法时,需要确定对模型的采样数m。 图6 为几何模型A 的分割误差俯视图(未进行误差优化),其中m为采样数,可见采样数从2 增加到10,分割误差基本相同。
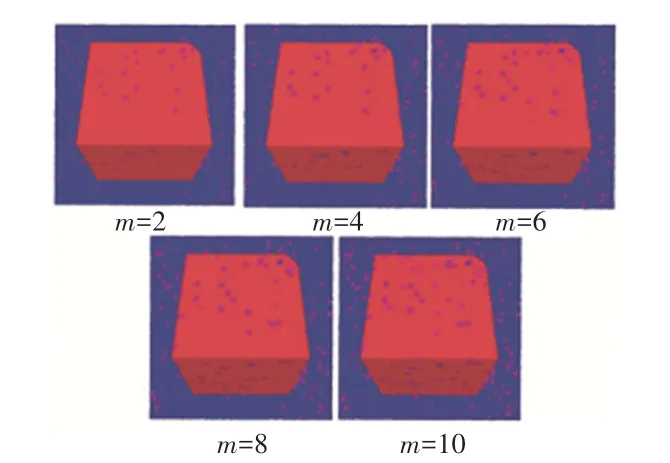
图6 几何A 模型不同采样数的分割误差俯视图Fig. 6 Top view of segmentation error of geometry A with different sampling numbers
采样数取不同数值时,对选取的16 个模型进行分割(未进行误差优化),并对结果进行定量比较,选组评估指标为兰德分数(Rand Score,RS)和运行时间,兰德分数用来衡量分割方法与基准的相似性,数值越大代表分割效果越好,实验结果如图7 和图8 所示。 可见采样数从2 增加到10,兰德分数基本持平,分割时间明显上升。 因此,本文选取采样数目为m=2。
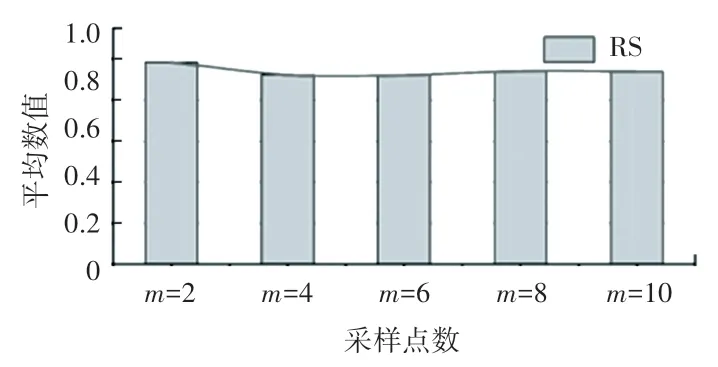
图7 测试模型不同采样数的兰德分数平均值Fig. 7 Average Rand scores of the testing models with different sampling numbers
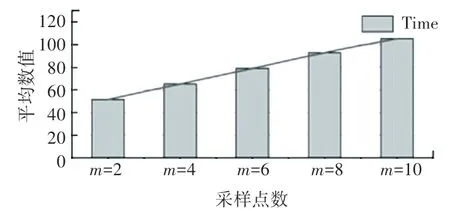
图8 测试模型不同采样数的运行时间平均值(/s)Fig. 8 Average running time of the testing models with different sampling numbers(unit: second)
本文方法对模型的二分割结果(每类模型中上方的命名为A,下方为B)如图9 所示,可以看出本文方法得到的分割结果符合人眼的视觉标准。
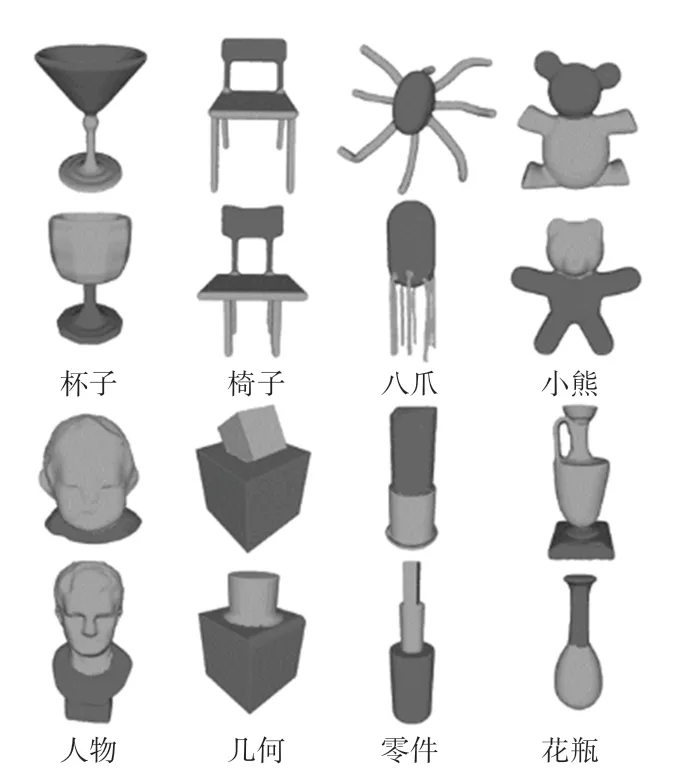
图9 本文方法对普林斯顿数据集部分细分模型分割结果Fig. 9 The segmentation results by the proposed method of partial Princeton dataset models after subdivision
对比指标除兰德分数外,还有准确率分数(Accuracy Score,AS)和汉明损失(Hamming Loss,HL)。 准确率分数与兰德分数类似,用来衡量分割方法与基准的相似性,其数值越大越好;汉明损失用来衡量分割结果中错误的比例,数值越小代表分割效果越好。
为进一步验证本文方法的有效性,采用量化评估标准将本文方法与BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies, BIRCH)算法,K-Means 算法,Mini Batch K-Means 算法,Liu等[5]提出的算法和Katz 等[13]提出的算法进行二分割比较。 实验结果如图10、图11 所示。 可见本文方法具有较好的分割效果,兰德分数、准确率分数高于其他算法,汉明损失低于其他算法。 在本文实验环境下,Liu 等[5]提出的算法和Katz 等[13]提出的算法仅可正常分割1 个模型,分割其余模型时超出16 GB内存限制,无法运行,因此无法显示这两种方法的指标平均值。
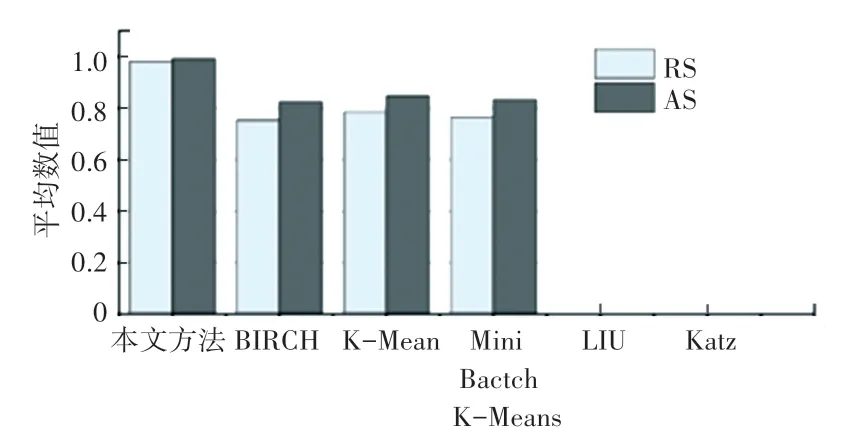
图10 测试模型兰德分数、准确率分数平均值Fig. 10 Average Rand scores,accuracy scores of the testing models

图11 测试模型汉明损失平均值Fig. 11 Average Hamming loss of the testing models
6 种算法在本文数据集上的兰德分数和运行时间见表1(本文方法已进行误差优化)。 在面片数最小的模型零件A (面片数3w)上,Liu 等[5]提出的算法获得了最高的兰德分数0.992,运行时间为397.3 s;Katz 等[13]提出的方法获得的次高的兰德分数0.988,运行时间为1 256.1 s,这两种方法在其余模型上均超出16 GB 内存限制,无法运行(数据在表1 中显示为横线)。 本文方法在零件A 模型上获得的兰德分数为0.986,高于其余3 种方法,运行时间为19.1 s;在其余模型上,兰德分数均为最高,运行时间在几十秒左右。
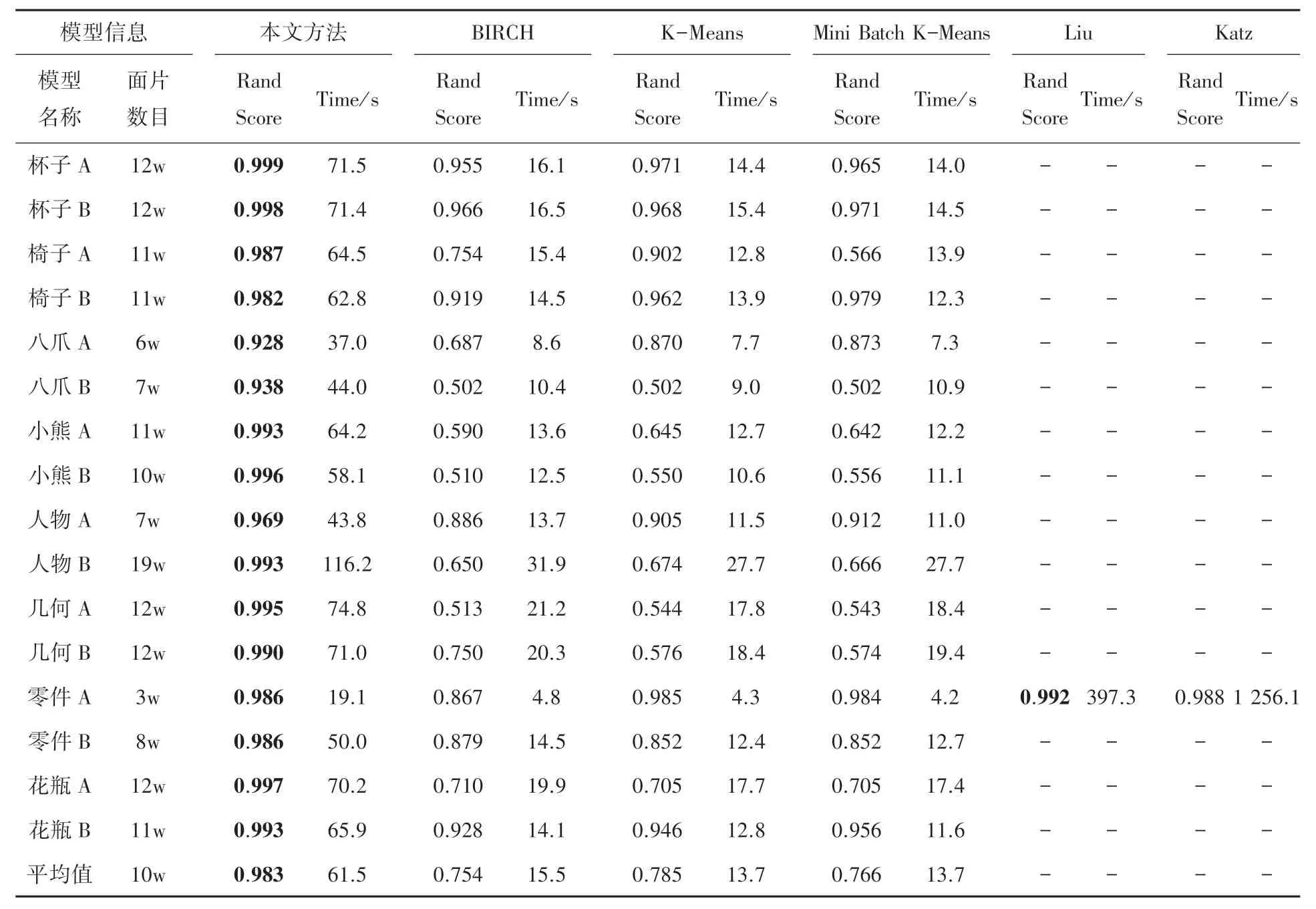
表1 测试模型兰德分数、运行时间评价表Tab. 1 Rand score, running time evaluation table of the testing models
传统谱聚类算法因其巨大的时间、空间开销无法分割面片数较多的模型;K-Means、BIRCH 等算法运行时间短、消耗内存空间小,但无法有效利用模型的几何特征,分割效果差。 本文方法相比于传统谱聚类算法,有效减少了分割模型所需时间、空间开销,同时也获得了较高的兰德分数,分割效果比KMeans、BIRCH 等算法好。
4 结束语
本文提出了一种结合Nyström 方法的三维网格模型分割方法。 首先,使用K-Means++算法对模型面心进行聚类,将距离聚类中心最近的面心作为采样点;其次,计算采样点和所有面心的亲和力数值,并使用Nyström 方法估计亲和力矩阵的主特征向量;将特征向量拼接为矩阵,并对矩阵每行元素使用K-Means 方法聚类,实现对模型的分割;最后,使用自适应邻域滤波算法对分割结果进行优化,去除估计误差。 实验结果表明本文方法有效避免了计算亲和力矩阵的时间、空间开销,可以获得符合人类视觉划分效果的分割结果。
本文使用Nyström 方法估计亲和力矩阵,存在一定分割误差,在二分割上取得了较好的效果,而对于多分割则会存在较大误差。 降低Nyström 方法的估计误差,更好地逼近真实的亲和力矩阵是接下来的研究重点。

