基于奇异谱分析和改进的BP 神经网络交通流预测
胡茂政, 张 剑, 王文翠
(上海工程技术大学航空运输学院, 上海 201620)
0 引 言
准确的交通流预测,可以帮助交通管理者做出合理的交通决策,并为旅行者提供更多信息,帮助旅行者们及时调整路线和改变旅行计划,因此已成为智能交通系统的重要研究热点。 此外,交通流预测对于保持交通流处于对称状态也大有裨益。 对称交通流的形成可以加快交通流的效率,缓解干道的交通拥堵。 然而,受气象条件、交通事故和道路养护施工的影响,交通流量呈现出高度的动态性、随机性和混沌性。 使得交通流量预测成为一个具有挑战性的问题
近年来,许多研究人员和学者研究了许多提高预测性能的方法。 主要的交通流预测方法大致可分为两类:传统统计学习方法和人工神经网络方法或混合神经网络方法。 传统的统计学习方法,如卡尔曼滤波[1]、自回归积分移动平均和贝叶斯方法等,这些方法过于简单,无法反映短期交通流预测过程中涉及的非线性因素,导致预测准确性较低。 人工神经网络[2]相比传统统计学方法,虽然预测效果有所提升,但如果忽略交通流数据的时间特征,人为获得特征会降低其信息的稳定性,还可能削弱模型的预期精度。
因此,为了探索精度和效率更高的预测方法,本文提出了一种SSA-IFA-BP 混合预测模型。 首先采用奇异谱分析法(SSA)对原始的交通流数据加以处理,去除噪声序列,保留有用信息;使用自适应权重的方法进一步优化萤火虫方法(FA),使其避免进入局部最优解;最后用改良的萤火虫方法(IFA)进一步优化BP 神经网络的加权和阈值,构建了SSA-IFA-BP混合预测模型,并使用该模型进行实验验证,实验结果表明,SSA-IFA-BP 模型相比于其他预测模型在交通流预测方面具有更好的预测精度。
1 理论基础
1.1 奇异谱分析
SSA 方法是一个基于相空间重建基本思想的全局分析方法,其中奇异值分解(SVD)可以识别原始信号分量(趋势、周期和噪音)。 该算法包含了分解和重构两个步骤。 分解过程中包含由一个嵌入操作和支持向量值组成。 而重构过程则包含分组和对角线的平均[3],具体步骤如下。
1.1.1 嵌入
在嵌入过程中,原始的一维序列P=[p1,p2,…,pN] 被转化为一个多维的轨迹矩阵X=[X1,...Xi,…,Xk],其中Xi=(pi,pi+1,…,pi+L)T∈RL,L是嵌入的维数(2 ≤L≤N/2),K=N-L+1。 轨迹矩阵X的描述如下:
1.1.2 SVD
通过对协方差矩阵的特征值分析,可以得出L的降部特征值为λ1、λ2、…、λL,以及相应的特征矢量U1、U2、…、UL。 通过采用SVD 方法,将轨迹矩阵X变换为
式中:d=max{i}(λi >0) 表示轨迹矩阵X的秩,Xi=√λiUiVT表示初等矩阵,Ui和Vi分别表示协方差矩阵S=XXT的左特征向量和右特征向量。√λ1≥…≥√λi≥0 表示轨迹矩阵X的奇异谱,最大特征值对应于最大特征向量,代表跟踪信号的趋势。 较小特征值对应的特征向量通常被认为是噪声。
1.1.3 分组
初等矩阵Xi(i=1,…,d)被分为m个不交叉子集I1、I2、…,Im,其中I={i1,…,ip}。 由此,公式(2)可以重写为
对给定的Ii,Xi的贡献率,可利用分解后特征值的百分比来计量。 在本文中, 得到贡献率等于0.1%w的r个奇异值,在d个奇异值中选取对其进行重建。
1.1.4 对角线平均
每个矩阵中XIn(n=1,…,r) 的对角线平均转化为一条边长为n的时间序列。 设一个子矩阵XIn为L×K,是带有元素xij的高维数矩阵如果L <K,则=xij;否则,=xji。 步骤3 中的子矩阵XIn通过式(4) 重构为相应的一维时间序列Rc=(rc1,rc2,…,rck,…,rcN)。
1.2 PSO 算法
一组粒子被随机建立,然后通过利用对该组粒子群中的个体极值和群体极值的确界,实现了某组粒子群的不断更新,使其作为粒子群算法实现的基础。 粒子速度的位置更新方法如下:
其中,vi,j(t+1)是粒子速度;xi,j(t+1)是粒子的位置;r1和r2为0~1 之间的两个随机数;c1和c2为学习因子;w是惯性权重,其公式如式(7) 所示:
式中:wmax和wmin为惯性权重最大值和最小值;t为当前迭代次数;tmax为设置的最大迭代次数值[4]。
1.3 GA 算法
遗传算法是在1975 年由约翰.霍兰德领他的研究生所创立,其主要思想依据是孟德尔的遗传学理论和达尔文的进化论[5]。 算法分为3 个部分,其中包括选择、交叉和变异。
(1)选择算法的计算公式为:
其中,fi是第i条染色体的适应值;pi是第i条染色体被选择的机率;N为样本总数;m为染色体的总数。
(2)交叉算法的计算公式为:
其中,和分别为A染色体在t位的交叉和B染色体在t位的交叉,a是0~1 之间的随机数。
(3)变异算法的计算公式为
其中,β是0~1 之间的随机数;xk是经过变异后的基因;xmin和xmax分别为基因边界的最小值和最大值。
1.4 萤火虫算法
1.4.1 萤火虫基本算法
萤火虫算法(FA)是为了解决YANG 于2002 年发明的数值优化问题而设计的[6]。 这个算法从萤火虫闪烁行为中得到启发,是一种有效的、概念简单且易于实现的元启发式的算法。 因此,许多研究者对萤火虫算法进行了研究,新的FA 变体被用来解决不同类别的优化问题,如连续、组合、约束、动态和噪声优化等。 寻优的原理为不断的去更正萤火虫的位置,最终找到定义下位置最好的那只萤火虫,寻优机制如下:
定义1萤火虫相对荧光亮度为
其中,I0是萤火虫当前location的亮度,光强吸收系数为γ,一般其取1;ri j则代表萤火虫i与j中间的欧式距离[7],式(13):
其中,xi,k是xi在空间中的第k个分量;xj,k是萤火虫xj在空间中的第k个分量;D是空间维数。
定义2萤火虫之间的吸引度βij公式为式(14):
其中,β0为初始位置的吸引度。
定义3萤火虫i因萤火虫j的作用,位置发生改变,其位置公式为式(5):
式中:xi、xj是萤火虫i、j的位置,α为步长因子,一般取0~1 之间的常数,t为迭代次数,εj是0~1 之间的随机数。
1.4.2 改进的萤火虫算法
萤火虫算法虽然在寻优问题中有着优良的性能表现,但仍然存在着天然的弊端,即在迭代后期,极容易陷入局部极值或者局部最优解。 由公式(14)可知,由于两个萤火虫之间距离增大,两者相对吸引力较小。 由此引发出一个问题,在极值点处,算法容易出现重复振荡,而公式(15)中的随机因子εj想要减小该振荡的影响,需要进行多次迭代。 为了避免或减少以上现象的影响,提出惯性权重对公式(15)进行优化,优化后的位置更新公式为式(16):
式中:w为惯性权重,表示当前位置对于原来位置的更新情况,通常取0~1 之间的常数。
为了让萤火虫在局部寻优的过程中更具针对性,先对惯性权重进行优化调整,使得惯性权重摆脱改变的随机性,能够根据目标函数的改变进行改变,其计算方法为式(17):
迭代过程中的萤火虫位置所改变的次数, 用o表示;λ(o) 反映惯性权重变化的平缓程度,值和其平缓程度呈反比,式(18)
式中:f(xi(o))是第i个萤火虫在经过o次位置更新的位置目标函数值,f(xbest(o)) 表示第o次更新后,位置最好的萤火虫的值。
1.5 BP 神经网络模型建立
1.5.1 BP 神经网络
通过对前馈网络的优化升级,BP 神经网络应运而生。 BP 神经网络包含输入、隐含和输出3 个层级。 其中,输入层节点数和输出层节点数分别为输入向量维数和输出向量维数,并随着研究问题及输入的不同,而对其进行针对性的调整[8]。 BPNN 算法的实现步骤如下:
步骤1输入X和输出Y呈映射关系,同时确定输入、输出神经元的节点和隐含层的节点数量。
步骤2以中间神经元(计为J) 为输入的输出(计为H),其计算公式为式(9):
式中:w为权值,b为阈值。
步骤3网络输出层计算公式为式(20):
步骤4实际数据与网络经训练后得到的输出值之间误差的计算公式为式(22):
步骤5在信息反向传递时,权值将按照误差e做出调整。 计算公式为
式中:η为学习效率。
步骤6当误差和设置值相比达到要求时,则终止迭代,否则转向步骤2 继续迭代。
1.5.2 萤火虫算法优化的神经网络
BPNN 由萤火虫算法改进的实现方式,主要是通过使用萤火虫算法的快速寻优能力,使得BPNN的权值和阈值都得以提高,从而提高BPNN 性能。具体实现步骤如下:
(1)建立BP 神经网络,初始化参数,设置隐藏节点数和隐藏层数;
(2)初始化FA 算法的个体及参数;
(3)设置萤火虫的种群数量和个体的适应度参数;
(4)更新每个萤火虫个体的信息;
(5)判断参数是否满足终止条件,满足条件转去执行步骤(6),否则返回步骤(4);
(6)将算法输出的最优权值和阈值代入到BPNN 进行训练和测试,计算误差;判断迭代次数是否已达到限制条件,若达到迭代次数最大值,则终止迭代输出补偿结果,否则循环执行步骤(6);
(7)生成最佳的FA-BPNN 模型。
2 交通流预测模型的构建
首先,使用奇异谱分析对原始交通流进行分解重构,剔除噪声干扰,利用处理后的数据作为IFABP 模型的输入,构建SSA-IFA-BP 预测模型。 利用遗传算法GA 和粒子群算法PSO 优化BPNN 的权值和阈值,使用原始数据作为模型的输入,构建GABP 预测模型和PSO-BP 预测模型。 通过实验对比,验证SSA-IFA-BP 预测性能。 预测流程如图1 所示:
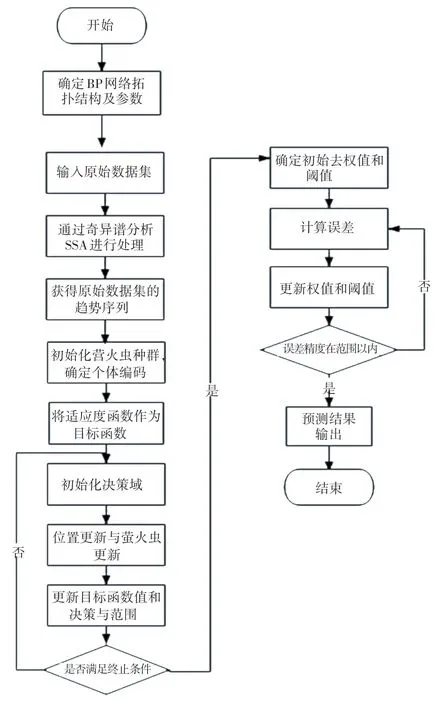
图1 SSA-IFA-BP 模型预测流程图Fig. 1 Flow chart of each SSA-IFA-BP model prediction
3 评价指标
为验证SSA-IFA-BPNN、 GA-BPNN、PSOBPNN 3 种预测方法的实际预测性能,本文采用两种误差评价指标,即均方根误差(RMSE) 和平均百分比误差(MAPE) 来反映模型预测性能[9]。
均方根误差(RMSE) 能够很好的反映预测数据偏离真实数据的程度,可以很好的反映预测的精确性。 平均百分比误差(MAPE) 能够整体的反映预测数据和真实数据的拟合程度,因此可以从整体上评价模型预测结果的离散性和精确性。 评价指标的公式如下:
式中:yi是在i时间点交通流预测值,yi0是该时间点交通流的现实数据,N表示数据的总个数,RMSE和MAPE值越小表示预测结果和原始数据的拟合性越好,预测的准确度越高。
4 仿真实验及分析
4.1 实验数据选取
交通流数据因受实际场景下各种复杂因素的影响(如路况、交通灯等),呈现出了不确定性和非线性,在对实际交通流数据进行分析时,采用matlab绘制时间序列曲线,可以看出其呈现出周期性的特征。 为了证明SSA-IFA-BP 预测模型在预测短时交通流数据性能的优越性,本文实验选取了美国加利福尼亚州高速公路PeMS 系统2019 年10 月6 日到10 月10 日的工作日数据作为实验数据。 该数据以5 min 作为采样间隔时间,共计1 440 个交通流数据。 本文采用的预测模型输入数据是预测时刻前两个小时的交通流时间序列,输出为下一时刻的交通流时间序列。 为了实现模型良好的拟合性,选取10 月6 号到10 月9 号的交通流数据作为测试集,共1 152个数据,建立了1 128 个输入输出集。 10 月10 号的交通流数据为测试集,共建立了288 个输入与输出集,时间序列曲线如图2 所示。

图2 五日交通流时间序列曲线Fig. 2 Time series curve of five-day traffic flow
4.2 奇异谱分析处理数据
在处理非线性时间序列数据中,奇异谱分析是目前较好的方法之一。 由于交通流数据呈现出非线性和不确定性的特点,因此在交通流数据的预测中,数据的特点不仅决定其预测的复杂性,同时交通流数据中的大量噪声序列,对于预测结果的准确性也构成了极大考验,而SSA 的出现,极大的解决了这一难题。 SSA 的基本原理为对原始数据进行分解、重构,将原始数据分解成不同成分的时间序列,剔除噪声序列,将其中贡献度大的时间序列进行重构。本文设置SSA 的窗口长度为L=8,将原始交通流数据利用奇异谱分析分解成8 特征分量(图3),从各特征分量的方差贡献率看,IMF1 和IMF2 的贡献率达到百分之98.67%。 所以,将两个子序列进行重构,得到新的交通流数据时间序列,即趋势序列,剔除剩下的分量所形成的噪声序列(图4)。 显然,趋势序列和原始交通流相比,在保留原始交通流数据变化趋势的同时,数据更加的平滑,更有利于模型的训练和预测(图5)。
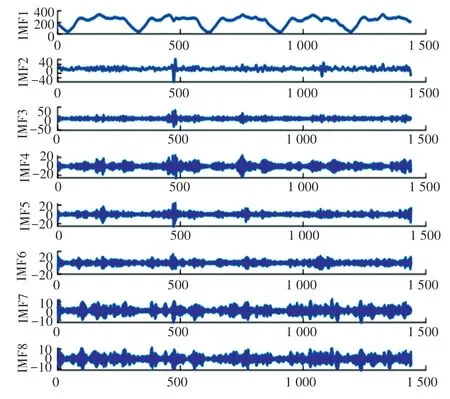
图3 奇异谱分析分解的特征分量Fig. 3 Eigen components of the decomposition of the singular spectral analysis
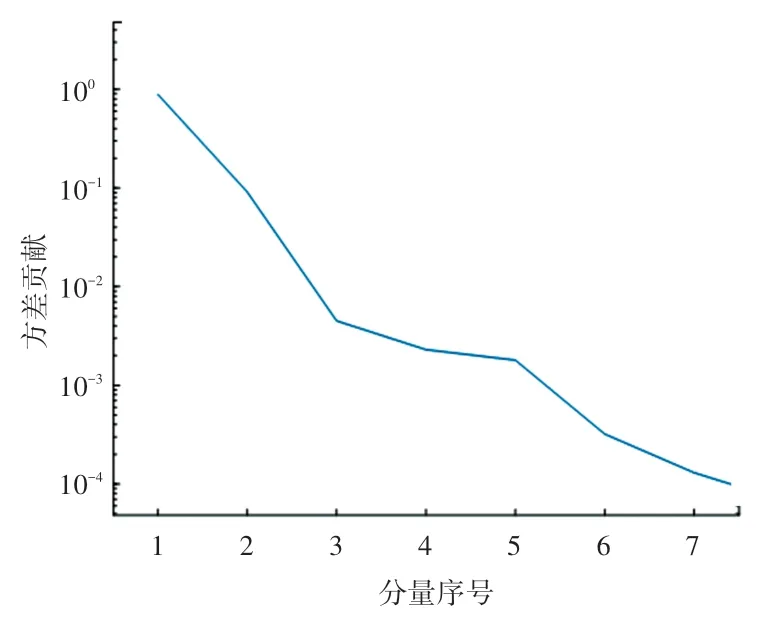
图4 不同特征分量的方差贡献Fig. 4 Variance contribution of the different eigen components
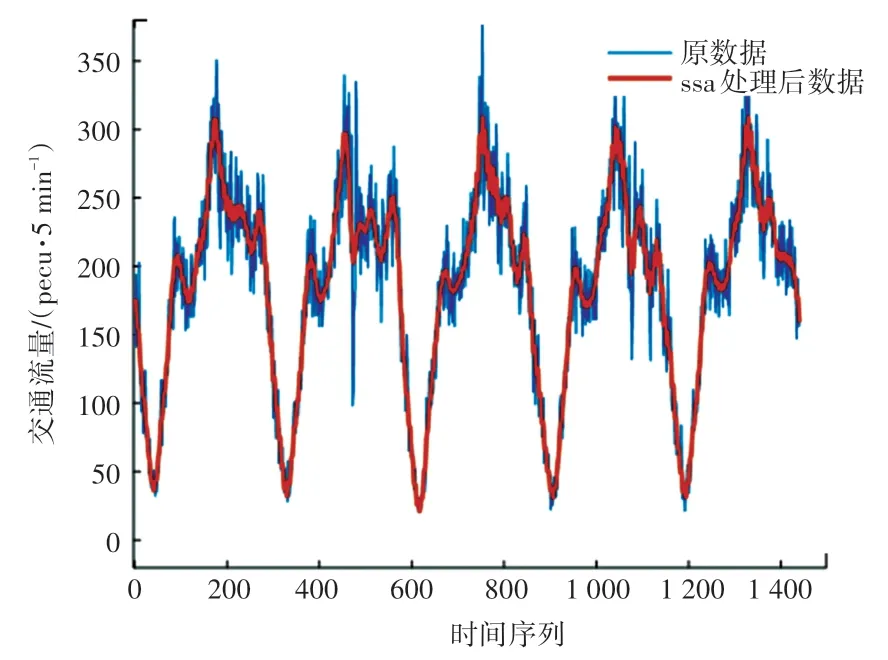
图5 原始数据和处理后的数据对比图Fig. 5 Comparison chart of raw data and processed data
4.3 仿真及分析
为了验证本文SSA-IFA-BP 模型在短时交通流预测方面性能的优越性,使用未经优化的BP 神经网络模型、原始数据未经SSA 处理作为模型输入的PSO-BP 模型、原始数据未经SSA 处理作为模型输入的GA-BP 模型的预测结果,与本文提出的SSA-IFA-BP 模型的预测结果和实际数据对比结果如图6 所示。

图6 不同预测模型预测结果和实际数据对比图Fig. 6 Comparison diagram of the prediction results and the actual data between the different prediction models
根据图6 的预测结果对比图可以看出,4 种预测模型对于交通流都可以进行良好的预测,但从各种模型的预测结果和原始数据的对比来看,各模型在预测性能上存在一定的差异。 从图中可以发现,BP 神经网络的模型曲线与原始交通流数据曲线比差别很大,该模型的检测结果在几种检测模式中属于较差的;PSO-BP 模型和GA-BP 模型,较BP 神经网络而言,两种模型的预测曲线和原始交通流数据曲线有明显的提升,说明经过粒子群算法和遗传算法优化后的BP 神经网络预测性能有所提高。 同时可以看出,GA-BP 模型相较PSO-BP 模型,其预测结果曲线和原始数据曲线的拟合更好,即GA-BP的预测效果更好。 SSA-IFA-BP 和其他几组预测模型相比,预测结果曲线和原始交通流数据曲线的拟合效果最好,对于交通流的预测效果是最好的。
由表1 可知,从误差的角度去评价各个模型的预测性能,BP 神经网络的预测误差,不管是RMSE还是MAPE都是最高的(分别为30.72 和7.9%),这说明BP 神经网络的交通流预测效果不佳;PSO-BP模型和GA-BP 模型在预测的效果上较BP 神经网络两项误差均有所减少,预测效果提升明显;本文所建立的SSA-IFA-BP 的预测误差在所有模型中最低,RMSE和MAPE分别低至22.64 和5.8,说明其预测性能在本文选取的预测模型里最好,也进一步证明了SSA-IFA-BP 模型在交通流预测方面预测效果的优越性。

表1 不同模型预测结果的误差对比Tab. 1 Error comparison of the prediction results of the different models
5 结束语
本文提出了一种基于奇异谱分析重构分解降噪,将萤火虫算法和BP 神经网络相结合的SSAIFA-BP 短时交通流预测方法。 首先使用奇异谱分析,对原始的交通流数据进行分解重构,提出对影响预测结果的噪声序列,保留趋势序列;针对萤火虫算法容易陷入局部最优的缺陷,提供了一个自适应权重的解决方案,对萤火虫算法进行了性能改善,并使用经过改良的萤火虫算法对BP 神经网络的权阈值进行了调整,提升其性能,并建立SSA-IFA-BP 预测模型。 通过与未经优化的BP 模型、GA-BP 模型以及PSO-BP 模型对于交通流数据的预测仿真对比,证明了本文提出的SSA-IFA-BP 模型对短时交通流预测性能的优越性。

