静态搅浑装置对核设施送风管气溶胶分布规律影响的数值分析
冉 鹏 顾卫国 聂保杰
(上海交通大学 核科学与工程学院 上海 201100)
送风管作为核设施通风系统的主要组成部分,其结构往往比较复杂,大量的弯头及管道形状的变化会迫使管道内部流场发生改变。目前,国内外对气溶胶粒子在弯头处的分布及扩散进行了大量的研究,受离心力及弯管形成的二次流的影响,气溶胶在管道内部的分布变得不均匀[1-2]。核电厂的放射性气态流出物监测取样的代表性与取样位置处的气溶胶分布均匀性有着直接联系,因此,需要提升取样位置处的气溶胶混合均匀性。针对这一问题,在风管中安装静态搅浑装置是一种可行的方法。
静态搅浑装置不仅可以用于固相和气相的混合,还可以用于其他多相之间的掺混,且对比其他混合方法,静态搅浑装置具有低维护成本、高混合效率及不需额外传动元件等优点。最早被商业化用于化工领域的是美国的Kenics型装置。我国对于搅浑装置的研究起步于20世纪70年代,衍生至今已经有较多的类型,但机械工业部将其归纳为5 种标准类型[3]。国内外学者在静态搅浑器上做了很多工作,部分学者研究了静态搅浑装置对流动阻力的影响[4-6],还有一部分学者对其传热性能做了分析[7]。对于静态搅混装置的混合性能,国内有学者通过简化的数学模型分析了旋流混合器对瓦斯的混合性能[8],另有学者通过数值计算的方法对分析了静态搅浑装置中元件个数、元件间隙以及元件的其他参数对于混合性能的影响[9-10],也对不同搅浑装置的混合性能进行了对比[11]。研究表明,采用静态搅浑装置能改善管道内部物质的混合均匀性[12]。因此,本文结合旋风式旋流混合器,设计了一种旋流静态搅浑装置,并在原本设计的基础上对装置的叶片宽度、叶片偏转角度进行调整,得到两种不同的结构。可以看到,送风管中气溶胶的分布均匀性在这种装置的作用下得到明显改善,能够大大提高核设施的放射性气态流出物取样监测的准确性。
本文针对核电厂的通风管道模型,采用数值模拟的方法,分析了三种不同结构的静态搅浑装置对流场以及气溶胶粒子分布规律的影响。
1 物理模型与模拟方法
1.1 物理模型
送风管模型如图1 所示,管道整体由0.4 m×0.4 m的方形管道、90°弯头、0.5 m×0.5 m的方形管道和直径为0.45 m的圆管组成。在空气入口处设置气溶胶粒子注入口,注入口的半径为10 mm。

图1 送风管物理模型示意图Fig.1 Diagram of physical model of air supply pipe
静态搅浑装置如图2 所示,搅浑装置原型为结构1,叶片分为内外两层,内层叶片逆时针扭曲,外层与之相反。结构2 只增大内外叶片的扭曲角度,结构3只增加内层叶片与外层叶片的面积比。搅浑装置的具体参数信息如表1 所示,其安装位置在圆管90°弯头下游,如图1所示。

图2 静态搅浑装置模型 (a) 结构1,(b) 结构2,(c) 结构3Fig.2 Model of static muddy device (a) Structure 1, (b) Structure 2, (c) Structure 3

表1 静态搅浑装置结构参数Table 1 Structural parameters of static stirring device
1.2 模拟方法与边界条件设置
本文对送风管道及搅浑装置均采用ANSYS ICEM CFD进行网格划分,网格类型为非结构网格。为进行网格无关性验证,计算了送风管的网格数量分别为100 万、400 万和1 500 万时同一位置处的风速(表2),对比发现,当网格数量为400 W时,具有较高的求解精度和求解效率。因此,送风管道的网格数量选择为400万,最大尺寸为30 mm,并划分三层边界层;搅浑装置最大网格尺寸为8 mm,网格总数量约为15万,如图3所示。

表2 不同网格数量下的风速对比Table 2 Comparison of wind speed under different grid numbers
本研究使用ANSYS CFX 软件进行模拟,气相流场选用对二次流和旋流等复杂流动有着较高求解精度的RNGk-ε模型。空气速度入口设置为亚音速速度入口(Normal Speed),参照某核电厂实际运行工况,将风速大小定为6.465 7 m·s-1。根据取样标准中的推荐,模拟采用的气溶胶粒子是粒径大小为10 μm、密度为1 000 kg·m-3的液滴[13]。在注入口均匀注入1×105个气溶胶粒子,为防止气溶胶注入时对流场的干扰,将粒子注入的初始速度设为0.5 m·s-1。出口设置为静压出口,压力等于大气压。重力方向沿着-y,重力加速度为9.8 m·s-2。离散相采用离散粒子模型(Discrete Phase Model,DPM)进行计算,由于固相体积分数低于10%,故选择单向耦合方式。对于小粒径且低体积分数的球形粒子,除考虑粒子受到的重力与浮力外,需要将Drag Force 设置为Schiller Nuamann,同 时 考 虑Non-drag Force 中 的Turbulence Dispersion Force 项。壁面设置为无滑移壁面,同时设置粒子撞击到壁面后被完全吸附。
2 计算结果
2.1 圆管段气溶胶分布特性
图4 为管道中的流线图。从流线图分析得知,该管道流体受直角弯头的影响,流动形态发生变化。管道初始的4 个弯头距离较近,流体的方向改变剧烈从而形成了旋流,旋流沿管道发展较均匀后经直角弯头进入更大的方管,流体区域向外扩展后撞击到管道壁面形成部分回流。此后管径收缩,流体经90°弯头进入圆管区域,最后达到出口。
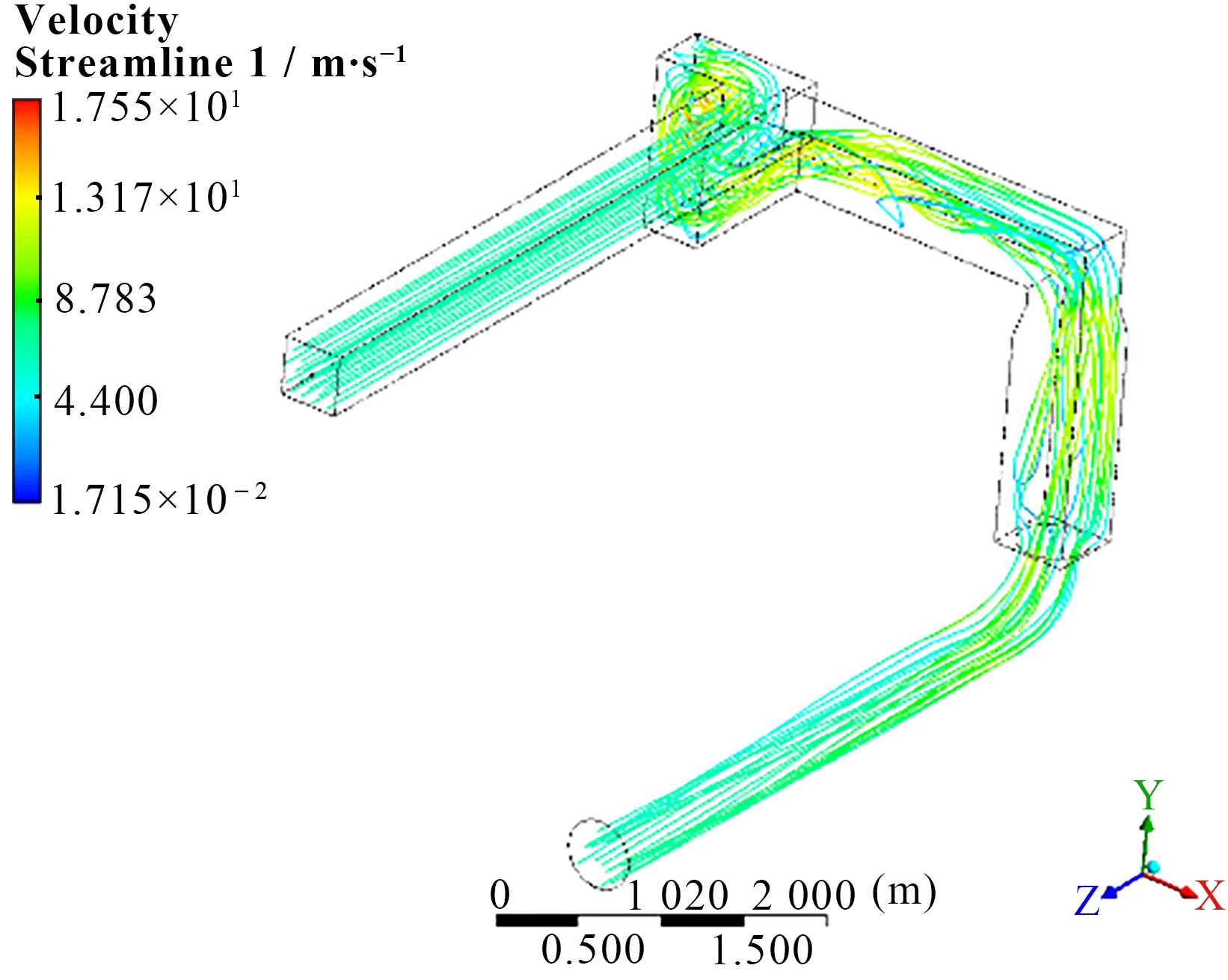
图4 送风管流线图Fig.4 Flow diagram of air supply pipe
本研究结合该模型实际取样区域,主要关注圆管段气溶胶粒子的分布特性。圆管段截面速度分布矢量图如图5 所示(以下所有图中的距离均指管道截面到搅浑装置出口的垂直距离),从图5中可以看出,受上游弯头影响,流体在进入圆直管段后分布并不对称,呈现出往管道下侧和右侧集中的趋势,随着管道高度的发展,在左上方区域形成一个涡,并逐渐向管道中心区域移动,流场的不均匀性虽有所改善,但右侧流场仍较左侧更为集中。粒子在流场中的运动受诸多因素的影响,本研究管道的初始雷诺数约为1.7 万,此时粒子主要跟随流场湍流扩散而运动,其他因素影响较弱。图6为对应截面的粒子浓度分布图,由图所示粒子浓度分布与流场特性较为一致。同时,随着管道高度的变化,越来越多的气溶胶粒子与管道壁面形成碰撞而被吸附,导致无粒子浓度的区域逐渐增多,粒子的总体浓度有所下降。

图5 圆管截面切向速度分布矢量图 (a) 距离0.2 m,(b) 距离1.4 m,(c) 距离3.0 mFig.5 Tangential velocity distribution vector diagram of circular tube section with vertical distance (from the cross-section of the pipeline to the outlet of stirring device) of (a) 0.2 m, (b) 1.4 m, (c) 3.0 m

图6 气溶胶浓度分布图 (a) 距离0.2 m,(b) 距离1.4 m,(c) 距离2.6 mFig.6 Aerosol concentration distribution with vertical distance (from the cross-section of the pipeline to the outlet of stirring device)of (a) 0.2 m, (b) 1.4 m, (c) 2.6 m
在取样代表性研究的标准[14],对于粒子浓度分布的均匀性有了量化的标准,即COV,计算方式如下:
COV值越小代表粒子浓度分布越均匀。图7为圆管段气溶胶COV随管道高度变化的趋势图,由图可知,气溶胶浓度COV在一开始随着流场不均匀性的改善有所降低,但在后续截面上由于粒子与壁面撞击导致零浓度区域的增多使得浓度COV 随距离的增加而升高。
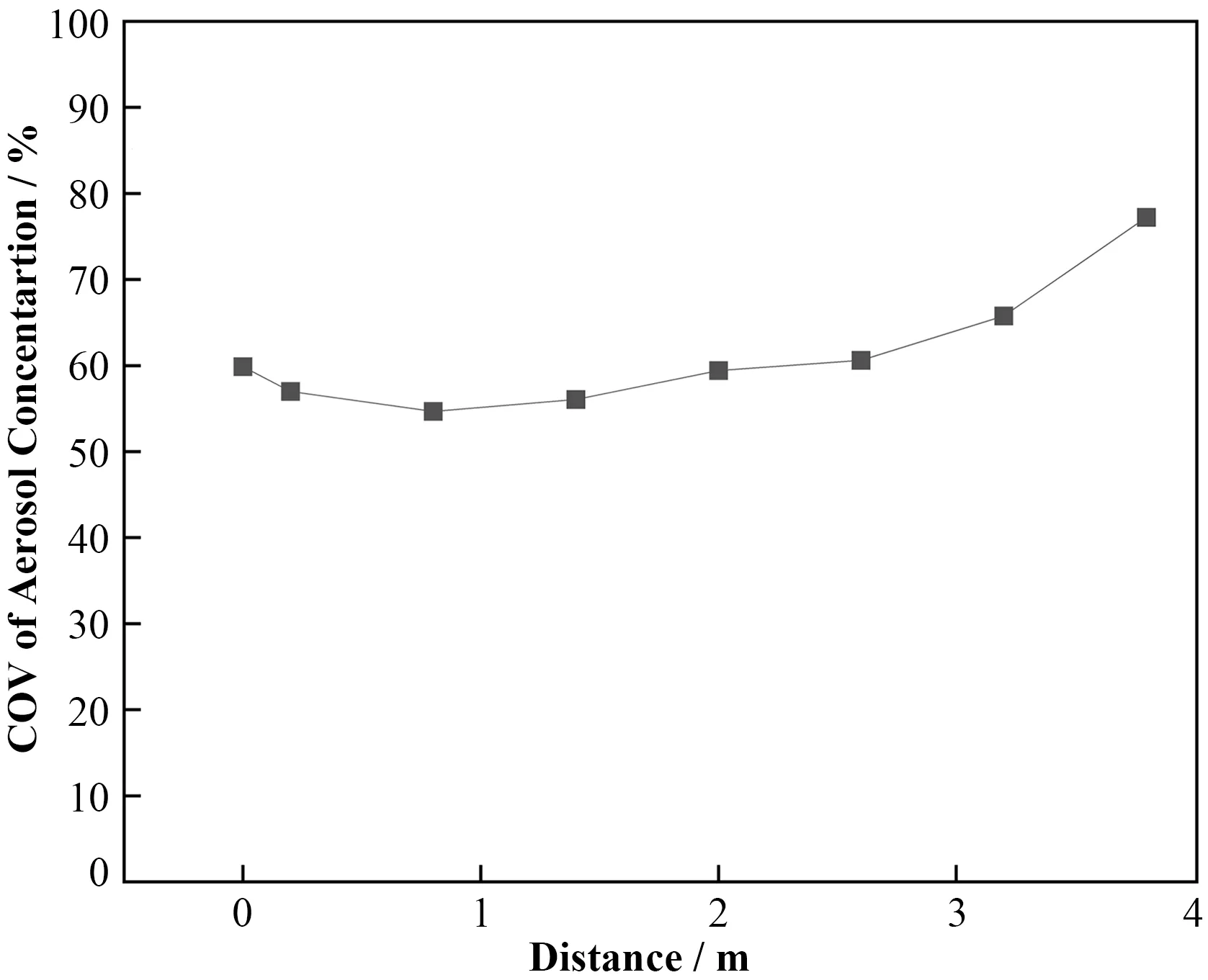
图7 浓度COV-距离变化曲线Fig.7 COV of concentration νs. distance
2.2 静态搅浑装置对气溶胶分布的影响
图8 为安装了结构1 的静态搅浑装置后不同高度截面的切向速度矢量图。从图8 可以看出,在距离搅浑装置出口较近的截面处产生了强烈的涡流,由于搅浑装置内外叶片的偏转方向不同,内外产生旋涡的方向也不同。随着距离的增加,中心区域的旋涡向外扩张后与外侧的旋涡发生碰撞,形成3 个强度较弱的涡旋,最终混合均匀,形成左右两侧较为对称的速度分布。中心区域的气溶胶粒子随着向外扩展的旋涡也向着管壁运动,在与外围的气溶胶掺混后又随气流向中心区域扩散,从而改变了气溶胶分布的均匀性,如图9所示。
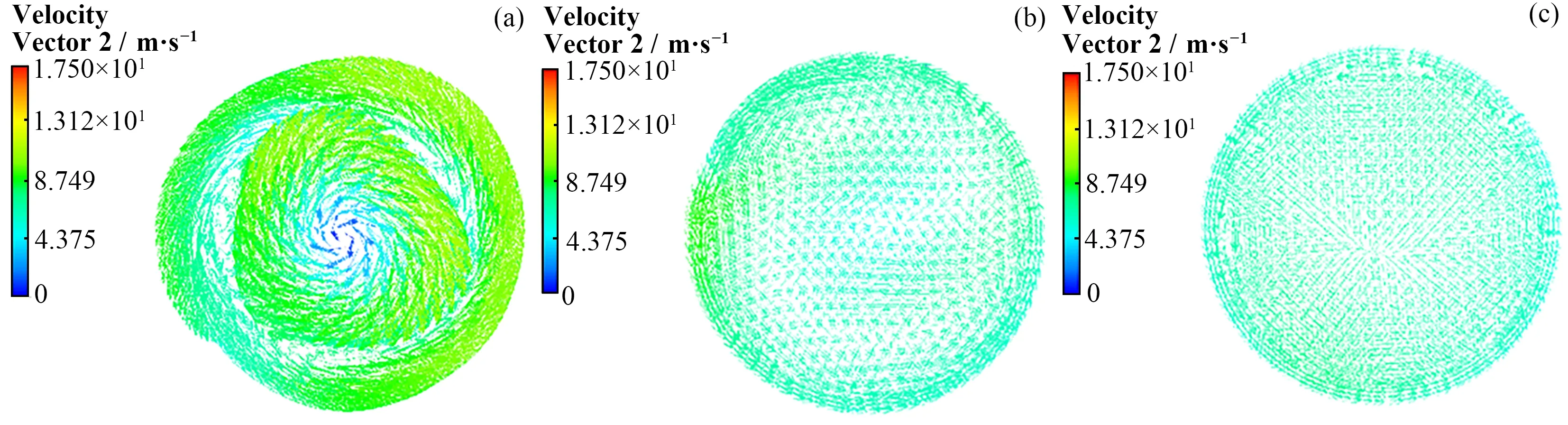
图8 结构1搅浑后不同距离截面速度分布 (a) 距离0.2 m,(b) 距离1.4 m,(c) 距离2.6 mFig.8 Velocity distribution of cross-section at different distances after mixing in structure 1 (a) 0.2 m, (b) 1.4 m, (c) 2.6 m
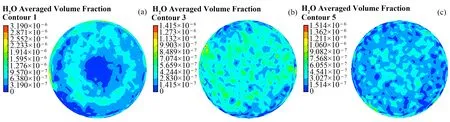
图9 结构1搅浑后不同距离截面气溶胶浓度分布 (a) 距离0.2 m,(b) 距离1.4 m,(c) 距离2.6 mFig.9 Aerosol distribution of cross-section at different distances after mixing in structure 1 (a) 0.2 m, (b) 1.4 m, (c) 2.6 m
不同结构的搅浑装置对管道内流场的影响并不一致,为判断其影响,对不同结构产生的速度分布进行对比。图10为结构2和结构3在不同截面处的速度矢量分布图,在距离为0.2 m 的截面处,结构2 与结构3均在中心区域产生了较结构1(图8)面积更大的涡。结构3 在距离为1.4 m 的截面中心区域速度更大,并且形成了较为明显的涡,可以较好促进气溶胶粒子在管道中心区域的掺混。而结构1 和结构2在此截面处壁面附近区域速度更大,粒子在管道近壁面处的运动更为剧烈,增加了粒子与壁面碰撞的可能性。此后,速度分布随着距离增加变得更为均匀。
图11 为3 种结构在距离0.2 m 的截面处旋涡强度。从图中可以看出,增大搅浑装置的叶片扭曲角度以及内叶片所占的面积比均对旋涡强度有增强作用,其中结构2产生的漩涡强度最强,旋涡强度将直接影响气溶胶粒子的掺混效果。
加装搅浑装置前后气溶胶浓度COV 如图12 所示(以下图中No Str为无搅浑装置,No.1、No.2、No.3分别对应结构1、结构2、结构3)。从图12中可以看出,搅浑效果最好的装置为结构3,说明旋涡强度在一定程度上的增加会持续改善气溶胶浓度COV,但过大的漩涡强度会降低装置的搅浑效果,因为强旋流场会使粒子与壁面的碰撞加剧,从而导致粒子损失。同时,取样截面设置在搅浑装置下游1~3 m 内效果最好,在距离为2 m的截面处其COV值较未安装搅浑装置时分别下降了23.17%、18.16% 和30.60%。
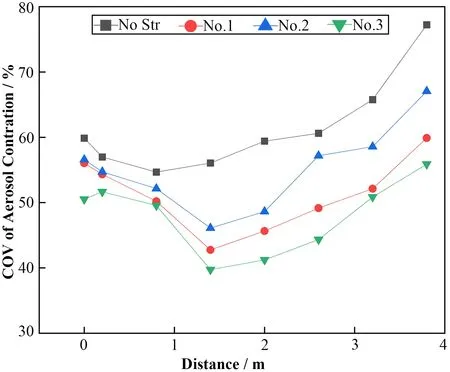
图12 气溶胶浓度COV随距离变化关系Fig.12 Variation of COV of aerosol concentration with distance
图13与图14为速度COV随距离的变化关系及平均气旋角的变化关系。在未安装搅浑装置时,气体速度COV 较大,随着距离的增加呈下降趋势,安装搅浑装置后,速度COV在较短的距离内有着明显的改善,受出口影响,速度COV 在较远距离的截面处有所上升,几种结构最后趋于一致,总体仍低于无装置时。同样的,在距离为2 m的截面处,速度COV分别下降了53.26%、60.04%和64.30%。而在安装搅浑装置后,搅浑叶片产生的强旋流使得平均气旋角在靠近装置处较未安装时剧烈增大,但随着距离的增加,内外气旋发生碰撞,平均气旋角陡然下降,最终几种结构的结果几乎相同,但总体仍高于未安装装置时。
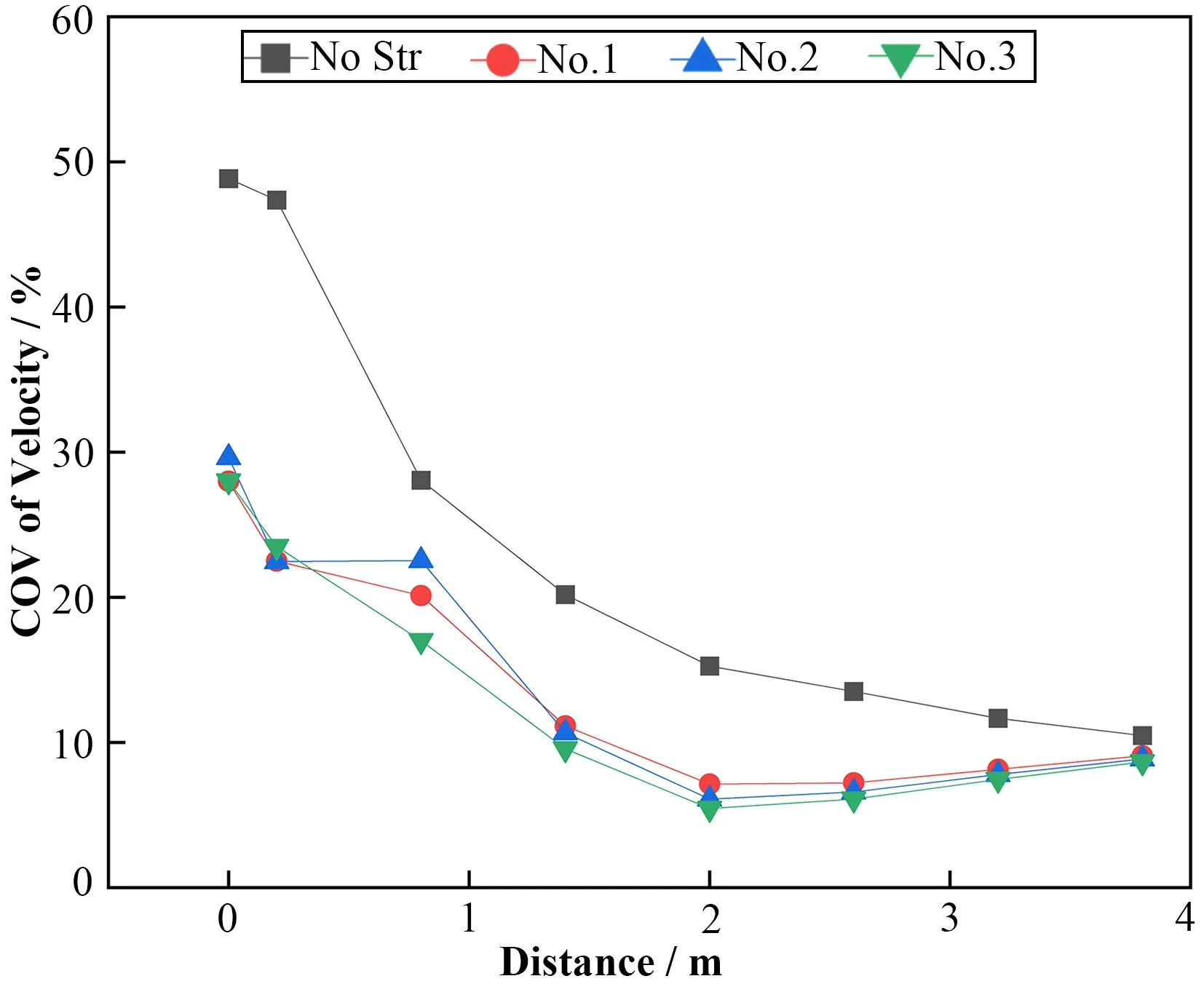
图13 速度COV随距离变化关系Fig.13 Change in COV of velocity with distance

图14 平均气旋角随距离变化关系Fig.14 Variation of mean cyclone angle with distance
3 结语
本文针对核设施通风系统送风管中的气溶胶行为进行了数值模拟,对不同结构的静态搅浑装置产生的影响进行了研究,得出如下结论:
1)管道结构的复杂性导致内部流场的特殊性,直角弯头以及管径变化等能引起流场激变的行为会影响气溶胶的扩散运动,同时可能会造成管道内气溶胶分布的不均匀性。
2)气溶胶浓度分布的均匀性并不随着管道距离的发展而提升,粒子与管壁的碰撞形成的零浓度区域的增加亦可能导致其分布不均。
3)静态搅浑装置能在出口处产生强烈的涡,不同结构产生的涡强度不同。旋涡强度过大会降低气溶胶粒子分布的均匀性。
4)静态搅浑装置能明显改善气溶胶分布的均匀性,其中增大内叶片所占面积的结构3效果最好,在距离为2 m 的截面处气溶胶浓度COV 较未安装时下降了30.60%。
本文针对改善核设施通风管道中气溶胶浓度分布均匀性这一问题,设计了静态搅浑装置,并分析总结了搅浑装置对气溶胶浓度分布规律的影响,双层旋流的静态搅浑装置能够有效提高气溶胶浓度分布的均匀性,可以为辐射监测取样提供参考和依据。
作者贡献声明冉鹏负责搅浑装置设计、数值模拟及文章起草;顾卫国负责总体研究思路,搅浑装置设计改进,文章修订;聂保杰负责数据分析,文章修订。

