道路上跨影响下的地下管道沉降特性研究

蔡新森

（中交城乡建设规划设计研究院有限公司，湖北 武汉）

引言

随着我国交通事业的发展，工程施工不可避免的会对周边建筑产生影响。为了研究施工过程对建筑的影响，减少对周边建筑的破坏，学者们进行了大量研究。

孙祖望等人提出了双向自由度动力学模型[1]；杨人凤等人建立了冲击+振动+静碾复合动态系统模型[2]；陈超通过试验，分析了振动压路机对不同土质填土压实度的影响[3]；杨兴哲等人通过室内试验结合数值模拟的方法，研究了低路堤施工对周围结构的影响[4]；冯牧、雷晓燕等人通过模型分析，研究了列车行驶影响下的建筑物振动特性[5]；王继伦等人通过试验和数值分析，研究了煤矸石路基的工程力学特性[6]；王艳等人通过有限元模型，分析了土中应力随土体深度的变化规律[7]；肖伟等人通过研究得到了振动轮- 土体的动力学微分模型[8]；张志峰等人通过研究得到了振动压路机下土体竖向应力的能量分布图[9]；轩振华等人通过有限元模型，分析得到了填土在不同振频下的应力分布规律[10]；徐冉通过建立仿真模型，进行了压路机的减震性能研究[11]；张少宏、王勇、陈华卫等人通过研究粗粒土的流变特性，提出了相应的流变本构模型[12-14]。

随着雄安新区进入大规模建设阶段，道路建设中跨越地下管道的情况越来越多，为响应政府降本增效的政策，指导今后相似工程的建设，对地下管道在道路施工影响下的变形特性进行研究显得愈发重要。

1 数值模型的建立

本文基于雄安新区EA1 西段工程，建立了有限元模型。土体采用摩尔- 库伦本构模型，混凝土与铸铁采用弹性本构模型，材料参数如表1。

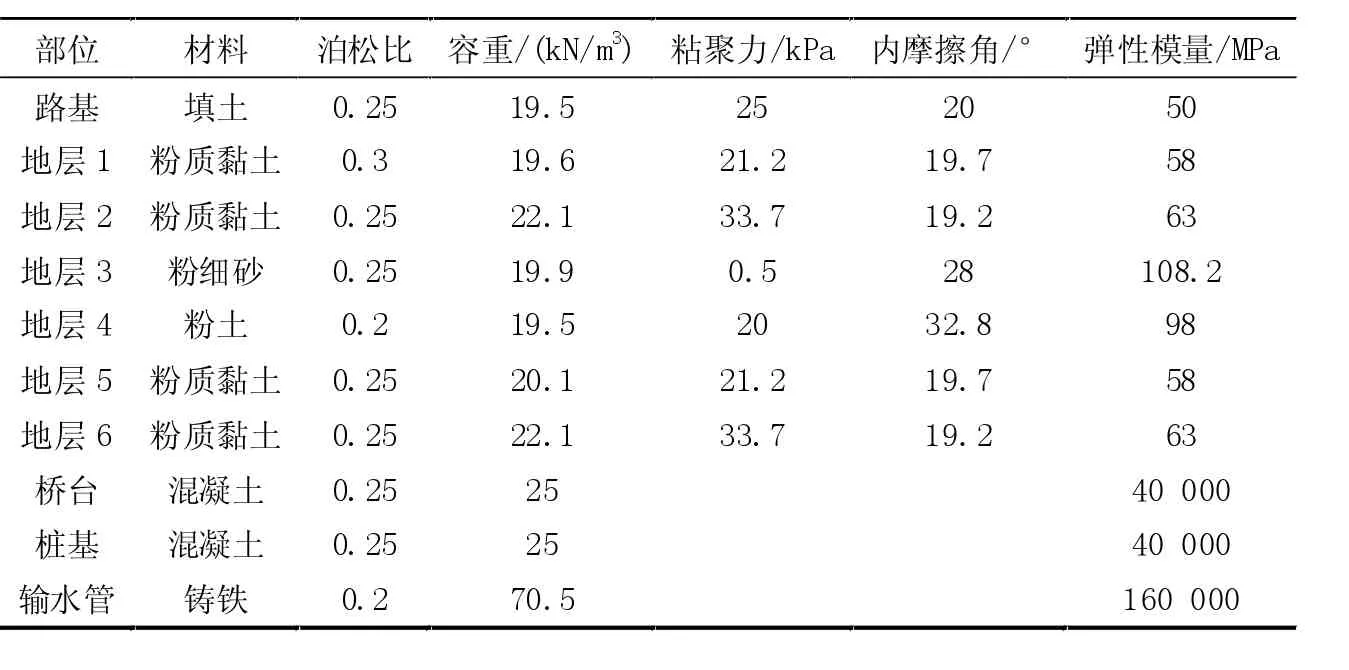
表1 模型材料参数

管道位于桥跨正中与路线正交，顶部距地面2 m，直径2 m；桩基为圆桩，桩径1.2 m，桩长40 m，桩间距4 m；桥梁跨径10 m。取模型长度、宽度、高度均为50 m，并将梁板和行车荷载等效为均布荷载处理，见图1-2。

图1 模型整体图

图2 钻孔灌注桩及管线单元剖面图

2 模型计算

2.1 计算阶段的划分

根据工程的施工和运营程序，将计算过程划分为几个阶段：（1） 初始阶段：生成模型，初始地应力平衡；（2） 桩基施工阶段：建立桩基构件；（3） 路基、桥台施工阶段：建立路基与桥台构件；（4） 桥梁施工阶段：在桥台上施加桥梁上部荷载；（5） 运营阶段：施加行车荷载。

2.2 模型计算结果

本文通过调整道路宽度和桥下净空高度建立模型，并对计算结果进行正交分析，计算结果如表2 所示。

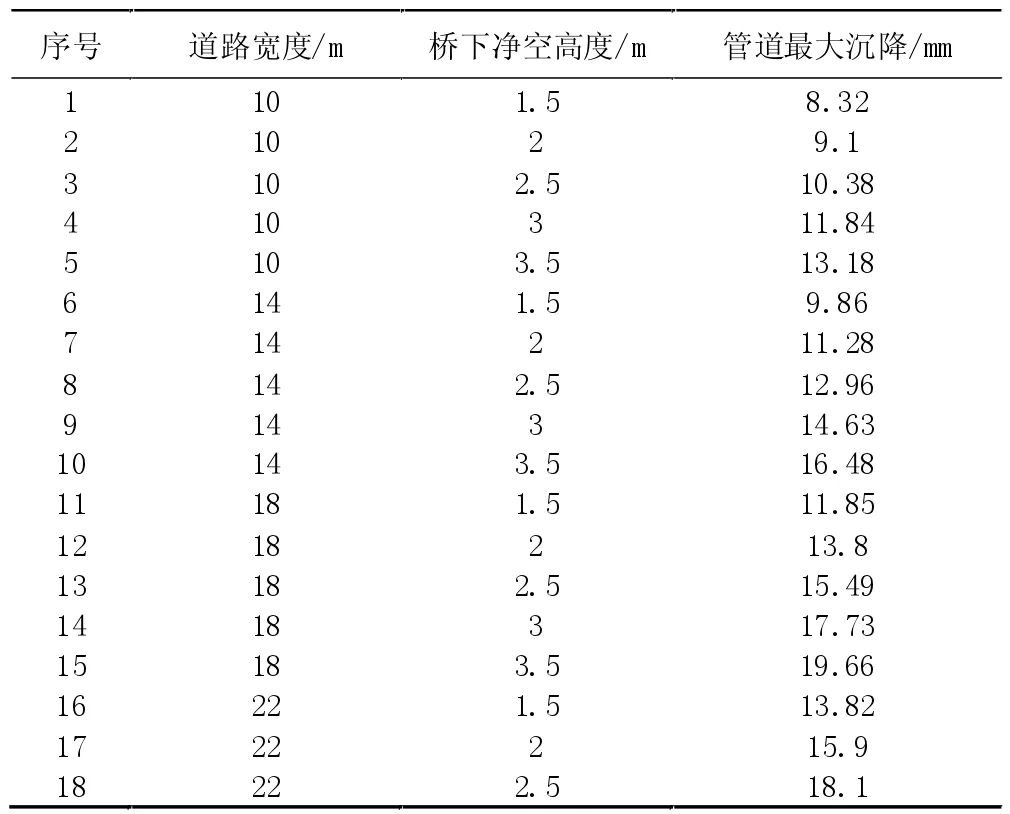
表2 管道最大沉降

3 计算结果分析

3.1 地下管线随桥下净空高度的变形特性分析

在道路宽度一定的条件下，对管线随桥下净空高度的变形规律进行分析，其规律如图3 所示。

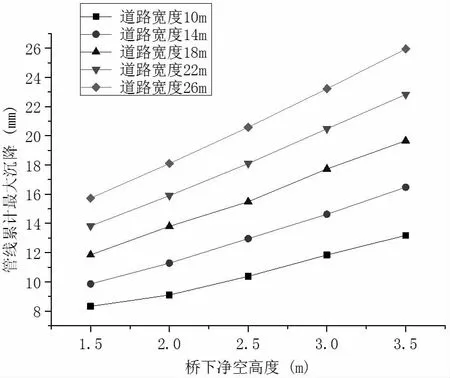
图3 管线最大沉降量随桥下净空高度的变化曲线

对图中数据进行拟合，得到了在道路宽度一定时，管线最大沉降量随桥下净空高度变化的回归模型如表3。

表3 管线最大沉降量随桥下净空高度变化的回归方程

对上述回归模型进行相关系数检验：当显著性水平a=0.05 时，R=0.878；当显著性水平a=0.01 时，R=0.959[15]，分析可知，上述回归模型拟合所得的R 值均大于0.959，即桥下净空高度与管线的最大沉降量具有十分显著的线性关系，利用P 值进行检验，由于P 值均小于显著性水平a，故可判定拟合所得的回归模型在1.5≤x≤3.5 的范围内成立。

3.2 地下管线随道路宽度的变形特性分析

在桥下净空高度一定的条件下，对管线随道路宽度的变形规律进行分析，其规律如图4 所示。

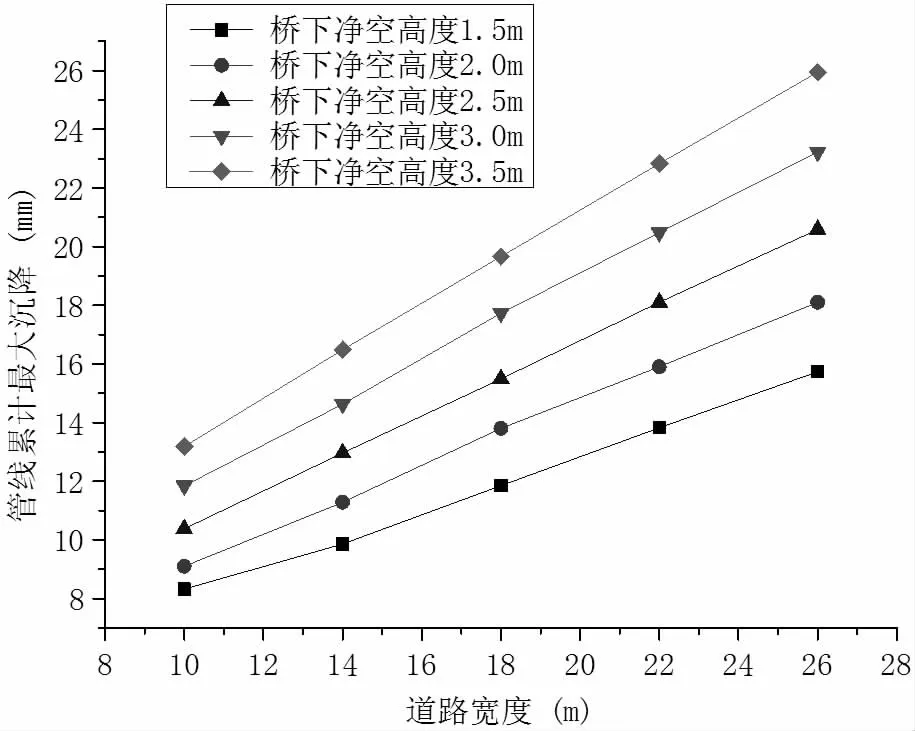
图4 管线最大沉降量随道路宽度的变化曲线

对图中数据进行拟合，得到了在桥下净空高度一定时，管线最大沉降量随道路宽度的回归模型如表4。

表4 管线最大沉降量随道路宽度的回归方程

对上述回归模型进行相关系数检验：当显著性水平a=0.05 时，R=0.878；当显著性水平a=0.01 时，R=0.959[15]，分析可知，上述一元回归模型拟合所得的R 值均大于0.959，即道路宽度与管线的最大沉降量具有十分显著的线性关系，利用P 值进行检验，由于P 值均小于显著性水平a，故可判定拟合所得的回归模型在10≤x≤26 的范围内成立。

3.3 多因素影响下的地下管线变形特性分析

经分析可知，管线的最大沉降量，同时受到桥下净空高度与道路宽度的影响，故对管线进行多因素变形特性分析，发现其变形规律如图5。

图5 多因素作用下的管线沉降变形特性

对变形规律进行多因素回归拟合，得到拟合关系如表5。

表5 管线最大沉降预测模型

对上述多元线形回归模型进行相关系数检验，经查相关系数的临界值表：当显著性水平a=0.05 时，R=0.878；当显著性水平a=0.01 时，R=0.959[15]，分析可知，上述多元回归模型拟合所得的R 值大于0.959，利用P 值进行检验，由于P 值小于显著性水平a，故可判定该回归模型在10≤x≤26 且1.5≤y≤3.5 的范围内成立。

4 结论

本文通过建立三维有限元模型进行分析，研究了道路施工影响下的管道沉降变形特性。得出结论与建议如下：

（1） 在道路宽度一定的情况下，管线的最大沉降量与桥下净空高度呈正相关，并得到了一元线性回归方程。

（2） 在桥下净空高度一定的情况下，管线的最大沉降量与道路宽度呈正相关，并得到了一元线性回归方程。

（3） 通过多因素回归分析，得到了在桥下净空高度与道路宽度双因素影响下的，管线最大沉降量的预测方程。

（4） 本文的研究成果仅适用于本项目，建议类似项目建设时仅可作为参照，应根据工程的具体情况进行针对性分析。