顶管技术对道路影响的有限元研究

武 创

（中冶南方城市建设工程技术有限公司,湖北 武汉 430077）

0 引言

随着城市化的不断发展，地下管线日趋复杂。旧管线因为老旧破损，造成排水不畅、路面塌陷等事故时有发生。为了解决现状管线的问题，传统开挖法新建和修复升级地下管道造成城市道路“开膛破肚”现场时常发生。而管道非开挖技术是能够解决“马路拉链”现象的最佳办法之一，具有综合成本低、施工周期短、环境影响小、施工安全性好等优势。

顶管法是管道非开挖修复中较为常用的技术，顶管法施工就是在工作坑内借助于顶进设备产生的顶力，克服管道与周围土壤的摩擦力，将管道按设计的坡度顶入土中，并将土方运走。作为管道非开挖实施技术的一种，顶管法有其他非开挖实施技术的优点：少开挖地面、不拆迁、不破坏地面建筑物、省时、高效、安全、综合造价低等[1]。

顶管法也存在一定的局限性，主要包括如下方面：

（1）施工时容易引起道路路基路面隆起，因此规范规定顶管覆土不得小于1.5 m[2]。

（2）施工时对临近的现状管道有一定影响，顶管法可能会损坏邻近的管道，因此当邻近的管线距离小于0.8 cm 或埋深小于0.8 m 时，建议不要使用该方法，或采取相应的保护措施[3]。

总结上述的问题，因为顶管施工时，顶进管道过程中会造成一定程度的土体挤压，所以对路基和相邻管线有一定影响。该文拟通过有限元模拟分析顶管过程中的受力过程，得出顶管过程中管道对土体的影响，并通过有效的技术手段，扩大顶管法的适用范围。

1 理论计算

1.1 基本理论

管道进入施工中引起土体变形的因素主要包括：

（1）地层损失造成沉降管道进入时，掘进面土体应力较大，土体会向管内移动塌落，由于土体的松动范围超出工具管范围，会造成进管周围的土层也被松动，因此地层有了损失。

（2）正面附加推力与土压力无法保持平衡，开挖面依靠附加推力与土压力的平衡保证稳定的出土，实际操作中，由于开挖面土质条件复杂，会有附加推力与土压力偏差较大的情况出现。若附加推力大于土体的被动土压力，会造成土体的挤压变形；若附加推力小于土体的主动土压力，则会造成土体的坍塌。

（3）管道进入与土体摩擦力带动周围土体移动。进管过程中掘进机以及后续管节均会对周围土体产生摩擦力，一般情况下掘进机与土体的接触面积更大从而产生更大的摩擦力。

（4）总竖向位移。地表竖向变形主要由地层损失、正面附加推力、摩擦力三部分即造成，因此总的地表竖向变形如下式所示：

式中，P—掘进正面附加推力（kPa）；D—掘进机外圈直径（m）；h—管道中轴线至地面距离（m）；G—土的剪切模量（MPa）。

经计算，地层土体损失+正面附加推力+侧面非均布摩擦力三者之和引起的竖向位移如表1 所示。

表1 沿纵断面变形量图——竖向总位移

1.2 计算研究结果分析

（1）管道进管对x、y 方向上的土体均有影响。

（2）对于y 和z 方向上位移关系，表现为距离管道操作断面距离越大，z 方向上土体位移越小，即影响越小。

（3）对于x 和z 方向上总位移关系，表现为z 方向上土体位移随x 不断变化，距离管道操作断面距离0~±8~9 m 不断增大，到±8~9 m 时出现极大值，然后不断减小，到±30 m 以上趋近于0。

2 模拟搭建

公式法依然有以下几个问题不能解决：

（1）公式法计算包括计算土体沉降、管道与土体之间的摩擦力、正面附加推力三部分内容，在计算正面附加推力时，由于现有公式无法计算已有管道通道的情况，因此在计算已有通道的管道进入时，采用的是折算迎面土压力Nf的方式来计算，虽然通过多组数据对比证明计算在常识上合理，但仍有逻辑不严谨的地方。

（2）公式法无法计算管道破坏后对地面承载力的影响，因此也无法验证采用何种手段加固的有效性。

（3）管道进入过程中，管道的顶、拉的力是一直变化的，而在公式法中管道的顶、拉力在一定的客观条件下被设定为恒定，这也是公式法存在的问题。

2.1 模型搭建

根据第一章公式法计算的结果表明，顶进管道、拖拉管道施工引起地面变形的因素主要包括土体损失、正面附加推力、管道与土体之间的摩擦力。其中，土体损失一般为土体产生沉降的主要原因，而正面附加推力、管道与土体之间的摩擦力会导致土体隆起。

为了克服传统公式法计算的问题，该文利用有限元软件对顶、拉管过程进行了三维动态模拟，采用位移贯入法克服了管道前进过程中推、拉力不断变化的问题，分析了顶管摩擦力对地表土体竖向位移的影响程度及范围，为施工对土体及周围建筑物的影响及其危害程度提供了参考。

2.1.1 模拟实验设计

该文拟研究管道在土体行进过程中对周围土体的影响，得出管道行进垂直方向（y、z 轴）上土体的位移[4-5]。研究包括：

（1）对比推入和拉入管道情况下的土体位移。

（2）对比是否预先排土情况下的土体位移。

（3）对比不同管中埋深下的土体位移。

2.1.2 模型参数

设定进入管道为钢管Q235，管壁厚18 mm 单根管节长6 m。设定自上而下地层依次如下：①层—淤泥质粉质粘土（厚4.0 m）；②层—粉砂（厚0.5 m）；③层—粉土。考虑顶管工程对土体影响的横向对称性，取1/2 土体进行模拟，土体范围为x 方向取-8~0 m，y 方向取-6~6 m，z 方向取0~12 m。

由于只考虑摩擦力对土体竖向位移的影响，因此模拟时不考虑土体的重力作用，同时假设同层土体为各项同性，各土层之间为水平分层。对开挖的土体采用生死单元进行模拟，如图1 所示，即开挖的单元随顶管的顶进逐步由活单元状态变为死单元状态。考虑到模型中顶力施加的变化，采用位移贯入法给定单位时间位移使顶管沿给定方向移动一定的距离（该文对顶管的动态模拟过程共采用了520 个增量步）。顶管及刀盘采用线弹性模型模拟，土体采用线性Mohr—Coulomb 弹塑性模型模拟，而在Marc 中Mohr—Coulomb 准则的屈服函数与Drucker—Prager 准则的屈服函数相同，其屈服函数F及相关参数α、бy分别如下：

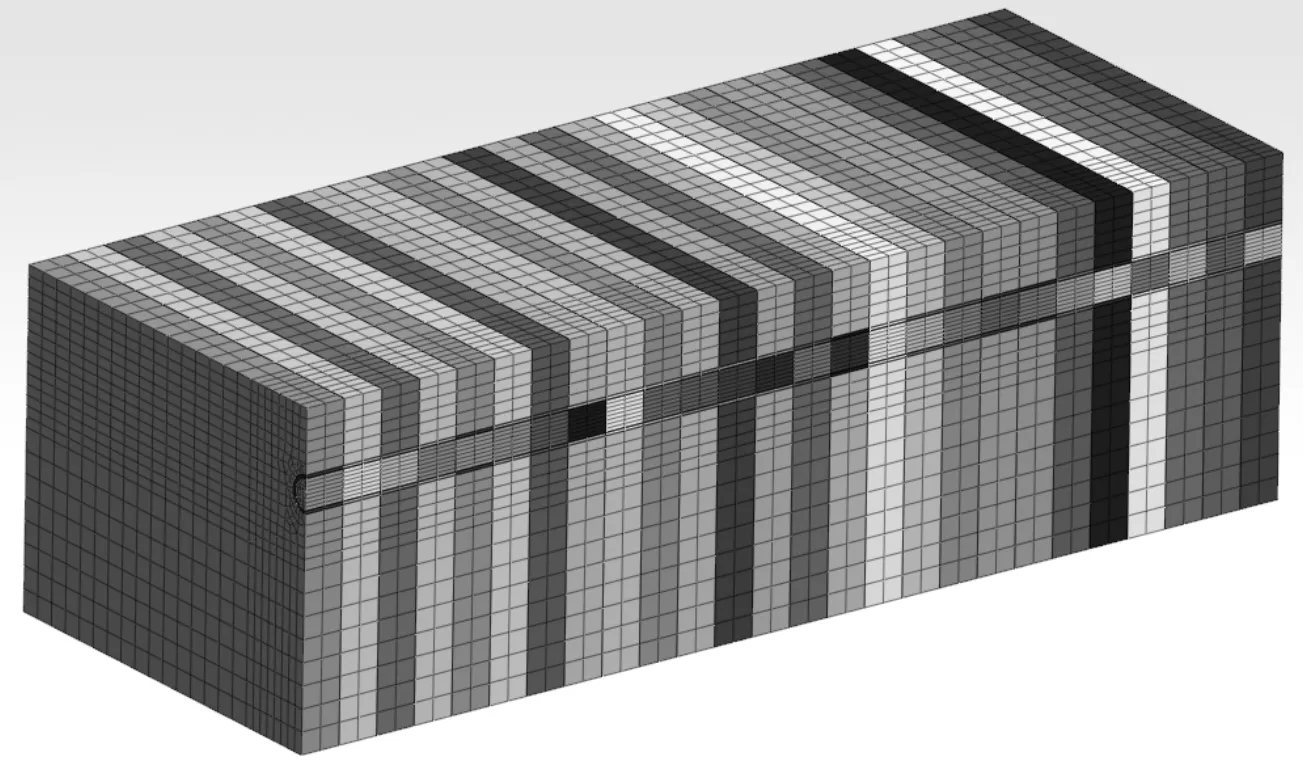
图1 管道计入过程模型建模图

式中，I1——应力状态第一不可变量；J2——偏应力张量第二不可变量；α、бy——应力不变量的函数；φ——内摩擦角；c——土体黏聚力。

该文采用Marc 软件中的库仑摩擦模型进行摩擦模拟。由于顶管处于层②中，因此仅考虑顶管钢管与层②的摩擦，对层①、层③与层②之间均采用黏合的接触分析。Marc 软件中对壳体单元的库仑定理描述如下：

式中，ft——剪切力；μ——摩擦系数；fn——法向反作用力；vr——相对滑动速度向量；rv——发生滑动时接触体之间的临界相对速度；t——相对滑动速度方向上的切向单位向量。

2.2 模拟结果及分析

2.2.1 对比是否预先排土情况下的土体位移

在相同管径、相同土体、相同埋深、相同推拉方式的前提下，预先排土与不预先排土两种情况在垂直方向上土体位移的比较，并得出相关结论，见表2。

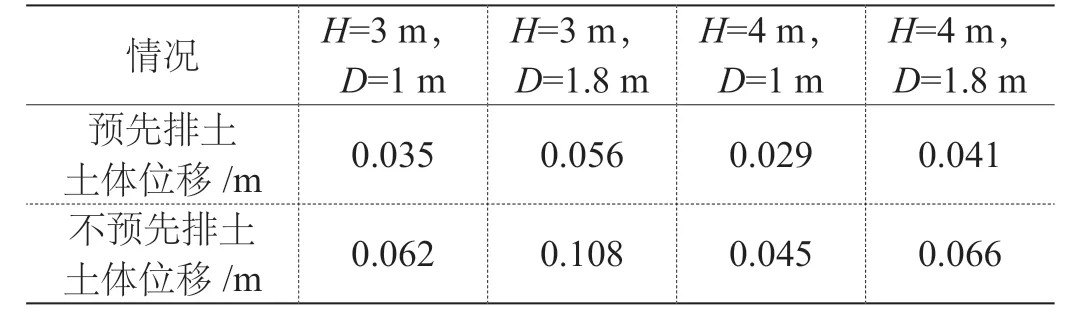
表2 预先排土和不预先排土情况下的土体位移 /m

从表2 数据分析可以得出结论：

（1）在相同管径、相同土体、相同埋深、相同推拉方式的前提下，预先排土情况下的土体位移相较于不预先排土要大得多，比如在H=3 m、D=1.8 m 情况下，预先排土位移值为0.056 m，而不预先排土的位移值达到了0.108 m。

（2）由于预先排土在土体位移数据上明显优于不预先排土的情况，因此后面的实验均在预先排土的假设下开展。

2.2.2 预先排土情况下，对比不同管道埋深下的土体位移

在相同管径、相同管材、相同土体、预先排土情况下，比较管道埋深为2 m、3 m、4 m、5 m、6 m 五种情况在垂直方向上土体位移（不同进管距离）的比较，并得出相关结论，见表3。

表3 不同管中埋深下的土体位移 /m

从表3 数据分析可以看出，管道上方土体位移随着管道埋深增大而减小、随着管径增大而增大。

2.3 结论

经过上面的有限元实验，得出下面的结论：

为了保证顶管工艺对土体上面的影响降到最低，在顶管前预先排土是必要条件。管道上方土体位移随着管道埋深增大而减小、随着管径增大而增大；为了让实施过程对路面有更小的影响，应探索能让土体位移更小、地面承载力损失更小的工程手段。

3 土体预先加固研究

管道在顶进过程中，对周围土体有一定影响，进而影响管道处正上方地面结构稳定性。下述旨在量化管道顶进过程中地面的受力，并研究使用超前小导管方法对土体进行加固后地面的受力，从而验证措施的作用和合理性。

3.1 管道稳定性研究

在相同土体情况下，分别比较1 000 m、1 500 m、1 800 mm 两种管径在管中埋深为2 m、4 m、6 m 三种情况下的地面的受力，见表4。

表4 不同管径在不同覆土下顶管的路面受力情况比较/kPa

3.2 小导管加固方法下道路稳定性研究

在相同管径、相同土体情况下，采用超前小导管加固后，比较管中埋深为2 m、4 m、6 m 三种情况下采用不用加固厚度（10 cm、20 cm）情况下的地面的受力，计算结果见表5。

表5 不同管径在不同覆土下顶管的路面受力情况比较/kPa

小导管加固的结论：

通过注浆加固的位移分布图和应力分布图，找到管道断面上的薄弱环节，在设置注浆加固方式时，在薄弱位置密集设置小导管，达到优化布置小导管的目的；通过施工前后、小导管加固前后的地面承载力对比，得出非开挖施工方法对路面承载力影响的数学关系，可用于判断具体实施方案的可行性。

4 结语

该文通过理论计算和仿真，量化性地研究了管道在非开挖扩容过程中管道对于路面的影响，对于研究管道顶管过程中的受力有着非常积极的作用：

（1）管道推入和拉入管道情况下，工艺对路面和周围管线的影响没有区别。

（2）不论管径大小，预先排土对控制地面形变和周围管线都有减小土体位移的作用。

（3）同样管径下，不同管中埋深下的土体位移也不一样，管中埋深越大，土体位移也越大。

（4）采用小导管加固能显著减少管道周围的土体位移，提高该施工方法的适用范围。