高强柔性索环与UHPC黏结性能理论分析

雷红兵,党隆基,庞 瑞,陈 莉,杨金鹏,李旭东,耿 佩

(1.中国建筑第七工程局有限公司,河南 郑州 450004;2.河南工业大学 土木工程学院,河南 郑州 450001;3.中建中原建筑设计院有限公司,河南 郑州 450004)

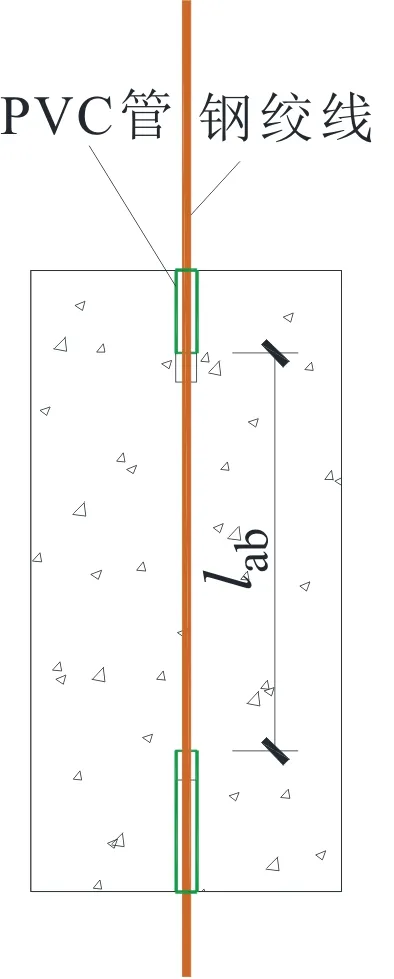
在国家“双碳”战略目标和新型建筑工业化重大需求牵引下,全面发展装配式建筑已成为我国建筑业结构调整和转型升级的必然途径。目前,我国流行装配整体式混凝土结构,此类结构中节点拼缝多采用后浇带连接、套筒连接和浆锚搭接,其中采用后浇带连接式的作业较多[1]。套筒连接和浆锚搭接存在钢筋对位困难、灌浆质量不易检测和施工繁琐等缺点[2]。与普通混凝土(Normal Concrete,简称NC)相比,超高性能混凝土(Ultra-high Performance Concrete,简称UHPC)具有超高强度、类金属拉伸强化特性和超高耐久性能等特点[3-4],其与钢筋黏结的合理锚固长度可减少至4d[5]。小直径钢绞线由高强钢丝捻制而成(见图1),与普通预应力钢绞线相比,具有较好的弯曲疲劳性能和冲击韧性。若以小直径钢绞线弯曲而成的高强柔性索环替代钢筋,并隐藏于剪力墙拼缝凹槽处,后浇带以UHPC替代普通混凝土,有望解决上述装配整体式混凝土结构节点拼缝连接存在的问题[6]。

a 钢绞线

现有研究多关注大直径钢绞线与NC或UHPC的黏结锚固性能等[7-8]。虽然也有小直径钢绞线与工程用水泥基增强复合材料(Engineered Cementitious Composite,简称ECC)黏结锚固性能的研究[9-10],但由于ECC与UHPC的材料性能差异较大,尚不能适用于小直径钢绞线与UHPC。此外,王海龙等[11]对钢丝绳与3D打印水泥基复合材料之间的黏结性能进行了试验研究。王红炜等[12]通过中心拉拔试验研究了高强钢丝绳与聚合物砂浆的黏结滑移性能,得到了钢丝绳锚固长度、钢丝绳直径和聚合物砂浆强度等对其黏结性能的影响规律。现有研究中,针对高强柔性索环与UHPC黏结锚固性能的研究鲜有报道。由于高强柔性索环具有螺旋肋,在拔出过程中会伴随一定的转动,导致其黏结性能与混凝土的黏结性能有明显的差异[13]。

本文以材料类别、锚筋和高强柔性索环直径等为参数,对高强柔性索环与NC和UHPC的黏结性能进行理论分析,给出了试件发生不同破坏形态时的临界锚固长度,可为高强柔性索环与UHPC在装配式混凝土结构中的应用提供参考和依据。

1 高强柔性索环-UHPC节点

考虑到小直径钢绞线具有良好的柔度、UHPC具有超高强度和类金属拉伸强化特性,庞瑞等[6,14]研发了高强柔性索环高效连接PC剪力墙的结构体系(简称新型PC剪力墙结构体系),即以高强柔性索环-UHPC节点(见图2)作为节点拼缝的主要连接形式。其设计理念为:高强柔性索环采用小直径钢绞线并通过压制锁扣制作而成,并锚固于剪力墙受力钢筋;竖向拼缝处界面为半圆形,后浇带以UHPC替代NC。与普通后浇带连接相比,该节点具有连接可靠,拼缝处的承载力较高、变形能力较好,预制构件天然粗糙面、侧面不出筋和平面外受力性能良好等优点。

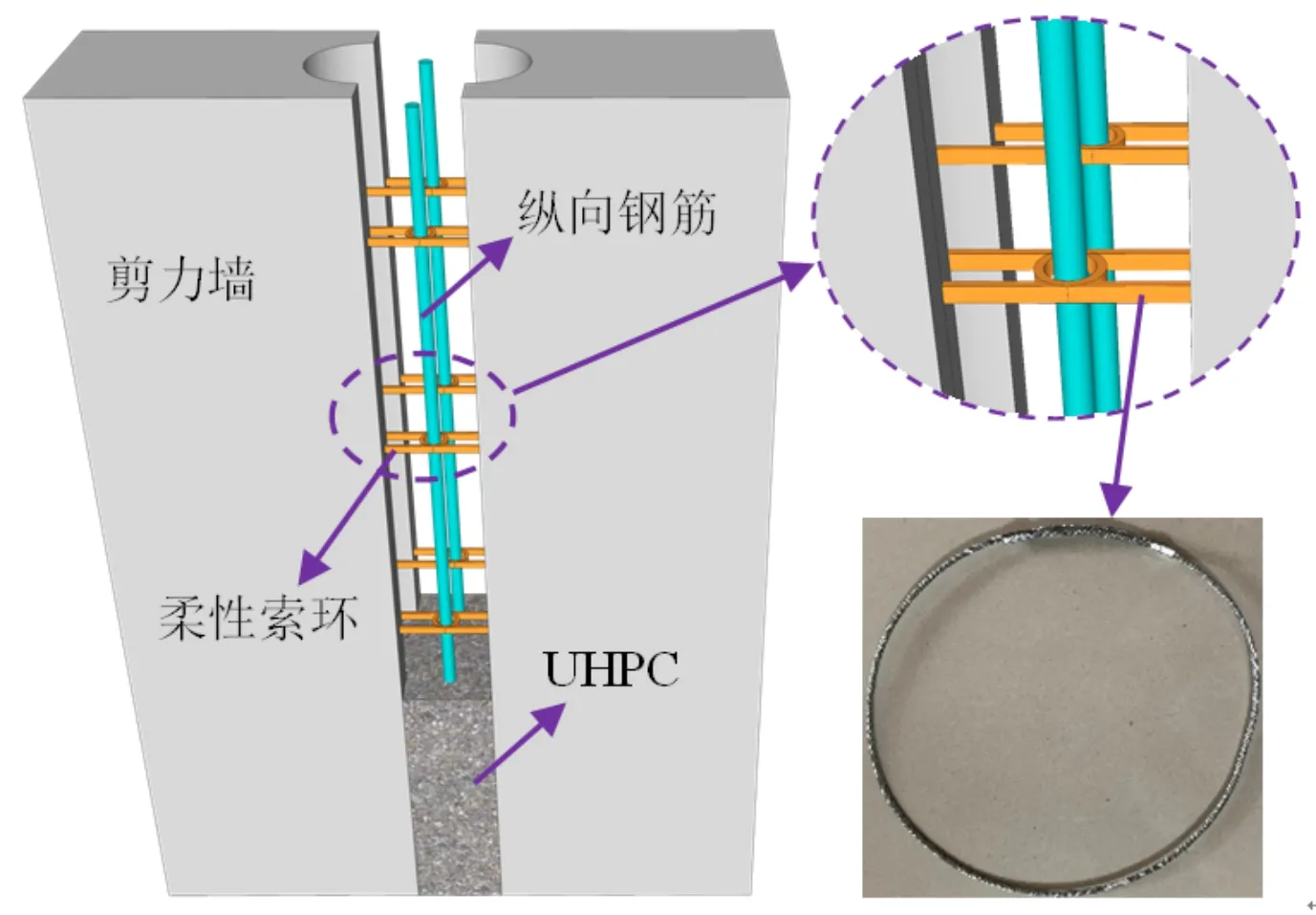
图2 高强柔性索环-UHPC节点

2 破坏形态

高强柔性索环是高强柔性索环-UHPC节点的重要组成部分,其与UHPC的黏结锚固性能对整个节点连接性能的发挥产生至关重要的影响。通常,高强柔性索环与UHPC黏结的主要破坏形态可分为混凝土锥体拔出破坏、黏结滑移破坏、混凝土全截面破坏和高强柔性索环断裂破坏等4种。这4种破坏形态的主要影响因素包括混凝土材料类别、高强柔性索环直径、高强柔性索环抗拉强度、销栓筋直径、销栓筋抗拉强度和高强柔性索环在混凝土中的锚固长度等。试件破坏形态示意图和简化的计算模型分别如图3和图4所示。图3和图4中,F为轴向拉伸荷载,d为钢绞线的直径,d1为销栓筋的直径,D为高强柔性索环的直径,τb为高强柔性索环与混凝土间的黏结力,σc为高强柔性索环圆弧段形成的部分混凝土压应力,τs为钢筋受剪所产生的剪应力,fy为销栓筋截面的抗拉强度,As为销栓筋的截面积。

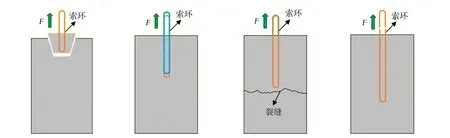
a 锥体拔出破坏 b 黏结滑移破坏 c 混凝土全截面破坏 d 高强柔性索环断裂破坏

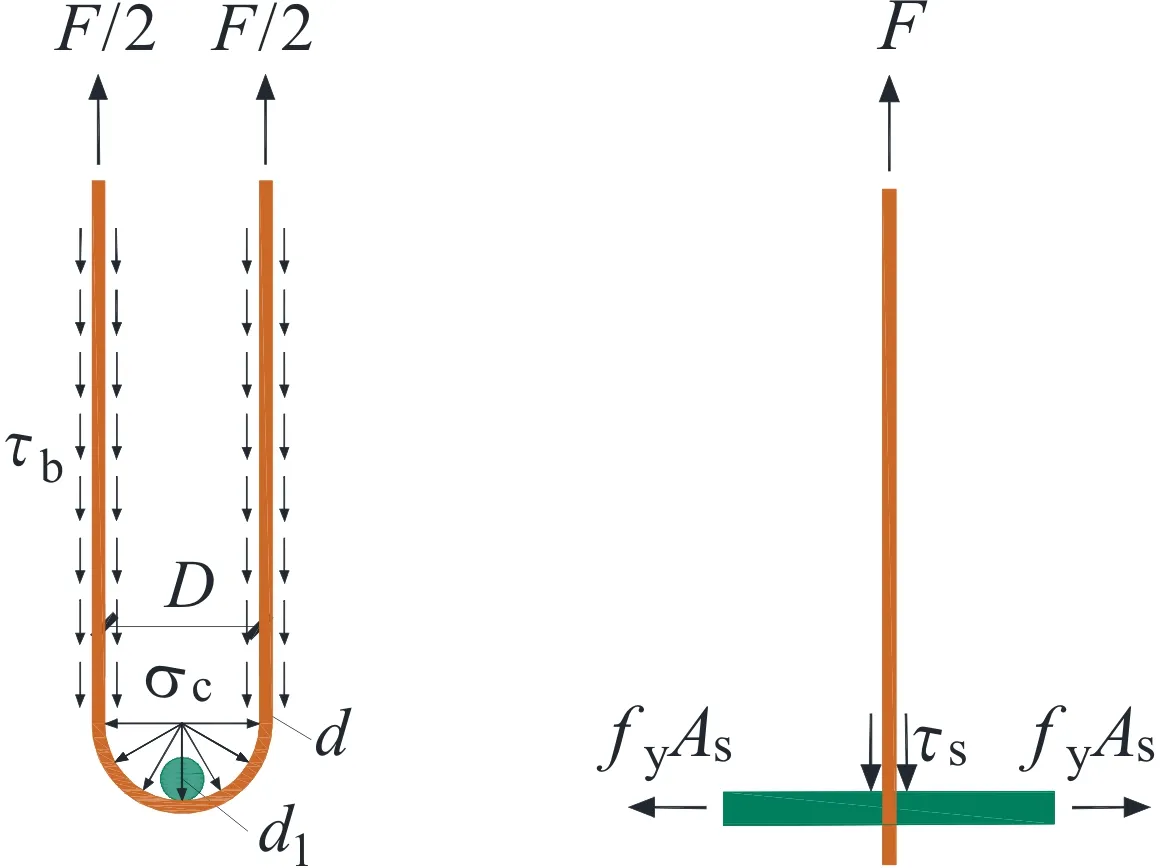
图4 简化计算模型

分析图4可知,当试件发生破坏时,轴向拉伸荷载主要由高强柔性索环与NC和UHPC间的黏结力、高强柔性索环圆弧段形成的部分混凝土压应力和钢筋受剪所产生的剪应力等组成。其中高强柔性索环与NC和UHPC间的黏结作用主要包括化学胶结力、机械咬合力和摩擦力。对于黏结滑移破坏,在加载初期,其黏结作用主要是化学胶结力,当荷载增大至自由端产生滑移时,黏结作用主要是高强柔性索环与NC和UHPC间的机械咬合力和摩擦力。

3 黏结锚固性能理论分析

3.1 混凝土锥体拔出破坏

当高强柔性索环在混凝土中的锚固长度较小时,高强柔性索环附近的局部混凝土由于抗拉强度不足将发生混凝土锥体破坏。根据其破坏形态,此时轴向拉伸荷载F可参考《混凝土结构后锚固技术规程》(JGJ 145—2013)[15]中的单根锚栓发生混凝土锥体破坏时的受拉承载力计算方法。

混凝土锥体破坏受拉承载力设计值为

NRd,c=NRk,c/γRc,N

(1)

式中:NRk,c为混凝土锥体破坏受拉承载力标准值;γRc,N为混凝土锥体破坏时的受拉承载力分项系数。

混凝土锥体破坏受拉承载力标准值为

(2)

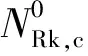
对于开裂混凝土,

(3)

对于不开裂混凝土,

(4)

式中:fcu,k为混凝土立方体抗压强度标准值;hef为锚栓有效锚固深度。

3.2 黏结滑移破坏

随着锚固长度的不断增加,在轴向拉伸荷载F的作用下,高强柔性索环与混凝土将发生黏结滑移破坏。在图4中,假定τb和σc沿钢绞线均匀分布,黏结应力Fb的计算公式为

Fb=πdlabτb

(5)

式中lab为高强柔性索环的锚固长度。

由于混凝土材料类别、销栓筋直径和钢绞线直径等对黏结强度影响较大,因此难以精确获得钢绞线与NC之间的黏结强度。为便于计算,NC与钢绞线的峰值黏结强度可参照Eligehausen等[16]建议的公式计算,即钢筋屈服前弹性状态峰值黏结应力的计算公式为

(6)

式中fc为混凝土立方体抗压强度设计值。

对于UHPC,当试件发生黏结滑移破坏时,其与钢绞线的黏结应力与锚固长度、保护层厚度、材料性能等有关,且黏结应力随着锚固长度的增加而减小[17],因此,本文参照文献[18]基于回归分析提出的GFRP筋与UHPC黏结滑移本构模型,将τb近似取值为22 MPa。

假定高强柔性索环的弯曲段为直径D的理想半圆。在高强柔性索环直径d的范围内以及轴向拉伸荷载F的作用下,高强柔性索环的弯曲段混凝土将产生压应力,其荷载的计算公式[19]为

Fc=0.5Ddσ

(7)

式中σc可按混凝土抗压强度取近似值。

(8)

(9)

式中:pmax为均匀分布在钢筋上的最大混凝土压力,是混凝土立方体抗压强度的3～4倍;E为混凝土的弹性模量;I为梁的截面惯性矩;c为梁的宽度。

已有分析[21]表明,销栓作用的最大值与钢筋的横截面积As、混凝土立方体抗压强度的平方根成正比,进而可将式(8)简化为

(10)

此时高强柔性索环所承受的荷载为

(11)

3.3 混凝土全截面破坏

当高强柔性索环在混凝土中的锚固长度超过临界值后,由于试件混凝土抗拉承载力不足以抵抗高强柔性索环与混凝土的黏结滑移荷载,试件将发生混凝土全截面破坏,此时轴向荷载最大值的计算公式为

F3=Acft

(12)

式中:Ac为混凝土横截面面积;ft为混凝土抗拉强度设计值。

3.4 高强柔性索环断裂破坏

随着锚固长度的继续增加,当高强柔性索环断裂破坏先于混凝土全截面发生时,此时轴向荷载最大值的计算公式为

F4=2Acyfcy

(13)

式中:Acy为计算用钢绞线截面面积;fcy为钢绞线抗拉强度。

4 临界锚固长度计算

4.1 理论值与试验值对比

选取文献[10]、[22]和[23]的试验结果验证上述理论计算方法的准确性,其中文献[10]的ECC和文献[22]的聚合砂浆均按照实测混凝土抗压强度等效为对应强度等级的普通混凝土,临界锚固长度试验值与理论值如表1所示。

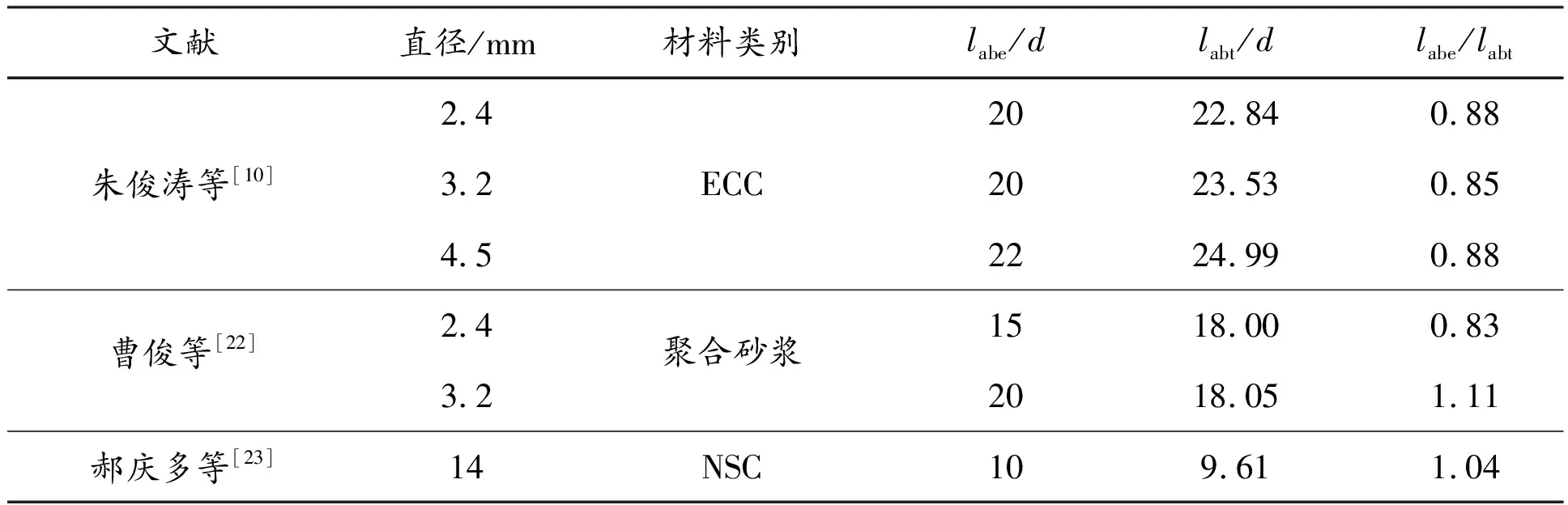
表1 临界锚固长度试验值与理论值

由表1可知,试件临界锚固长度理论值与试验值吻合较好,试验值与理论值误差介于4%～17%之间,考虑到临界锚固长度试验值的不精确性,因此本文所提出的理论计算方法可用于确定钢绞线在UHPC中的临界锚固长度。

4.2 算例分析

假定NC采用C40混凝土,fc=19.1 MPa,fcu,k=40 MPa,UHPC的抗压强度约为144.45 MPa,抗拉强度近似取7.05 MPa[24],钢绞线直径d为4.5 mm,抗拉强度设计值为1 110 MPa,抗拉强度的标准值为1 570 MPa,锚筋直径d1为14 mm。钢绞线直径为6 mm,高强柔性索环的圆弧段直径一般为45～65 mm[19],本文取40 mm。试件设计如图5所示。试件SC1为单根钢绞线,试件SC2为高强柔性索环,试件SC3在布置高强柔性索环的基础上增加了锚筋,3个试件的截面尺寸均为150 mm×150 mm。

a SC1

(1)混凝土锥体拔出破坏。

当锚固长度较小时,试件SC2和试件SC3易发生混凝土锥体拔出破坏,其危险截面是由混凝土控制,且需满足NRd,c≤2Fb+Fc,即

NRd,c≤2πdlabτb+0.5Ddσc

(14)

(2)黏结滑移破坏。

当锚固长度适当时,试件SC2和试件SC3将发生黏结滑移破坏,且当F2≤F3时,可求得试件发生黏结滑移破坏的最大锚固长度的临界值,即

(15)

(3)混凝土全截面破坏。

当试件截面尺寸为150 mm×150 mm时,随着锚固长度的不断增加,试件可能发生混凝土全截面破坏,此时需满足

(16)

(4)高强柔性索环断裂破坏。

随着锚固长度的继续增加,试件在发生混凝土全截面破坏前可能发生高强柔性索环断裂破坏可能发生混凝土全截面破坏,此时需满足

2Acyfcy≤Acft

(17)

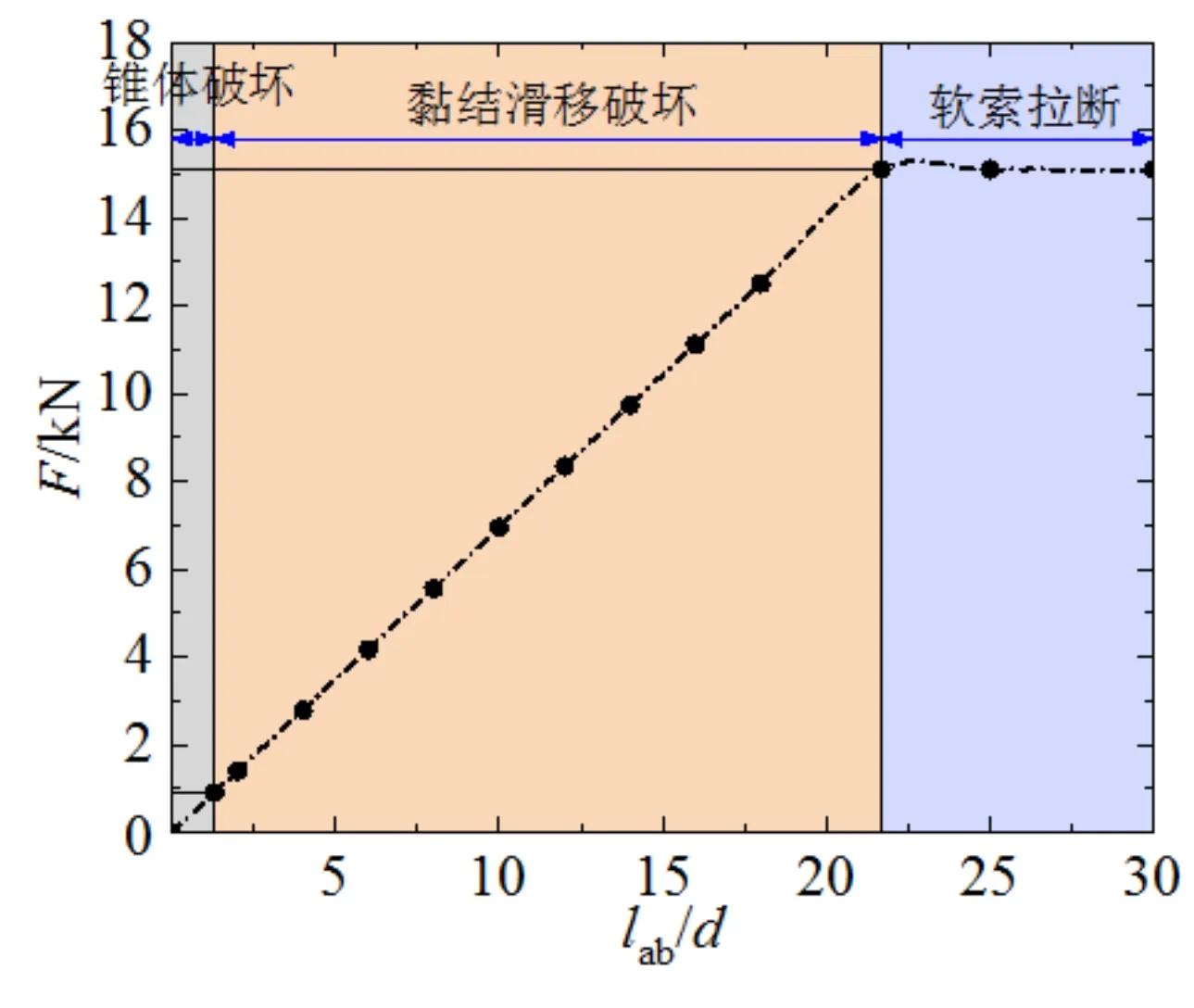
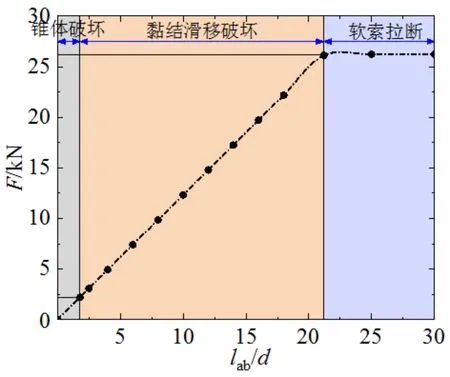
由以上分析可知,当试件SC1钢绞线直径为4.5 mm时,采用NC和UHPC发生锥体破坏的最大临界锚固长度分别约为1.3d和1.5d,钢绞线不发生断裂的最大临界锚固长度分别约为21.7d和10.8d,其荷载-锚固长度曲线如图6所示。当钢绞线直径为6.0 mm时,采用NC和UHPC发生锥体破坏的最大临界锚固长度分别约为1.8d和2.0d,钢绞线不发生断裂的最大临界锚固长度分别约为21.2d和10.5d,其荷载-锚固长度曲线如图7所示。

a NC

a NC

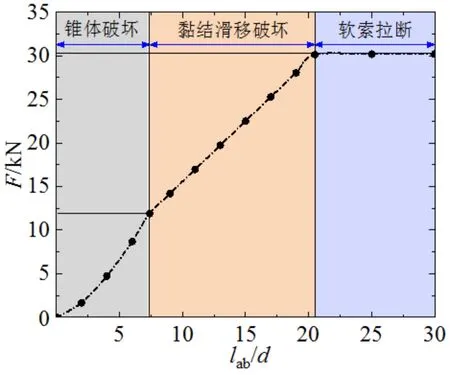
当采用NC且高强柔性索环的直径分别为4.5 mm和6.0 mm时,根据式(13)～式(15),试件SC2发生锥体破坏的最大临界锚固长度分别约为7.4d和8.8d,高强柔性索环不发生断裂的最大临界锚固长度分别约为20.5d和20.4d。当直径为6 mm且锚固长度大于14.7d时,试件SC2可能会发生混凝土全截面破坏,其荷载-锚固长度曲线如图8所示。

a d=4.5 mm

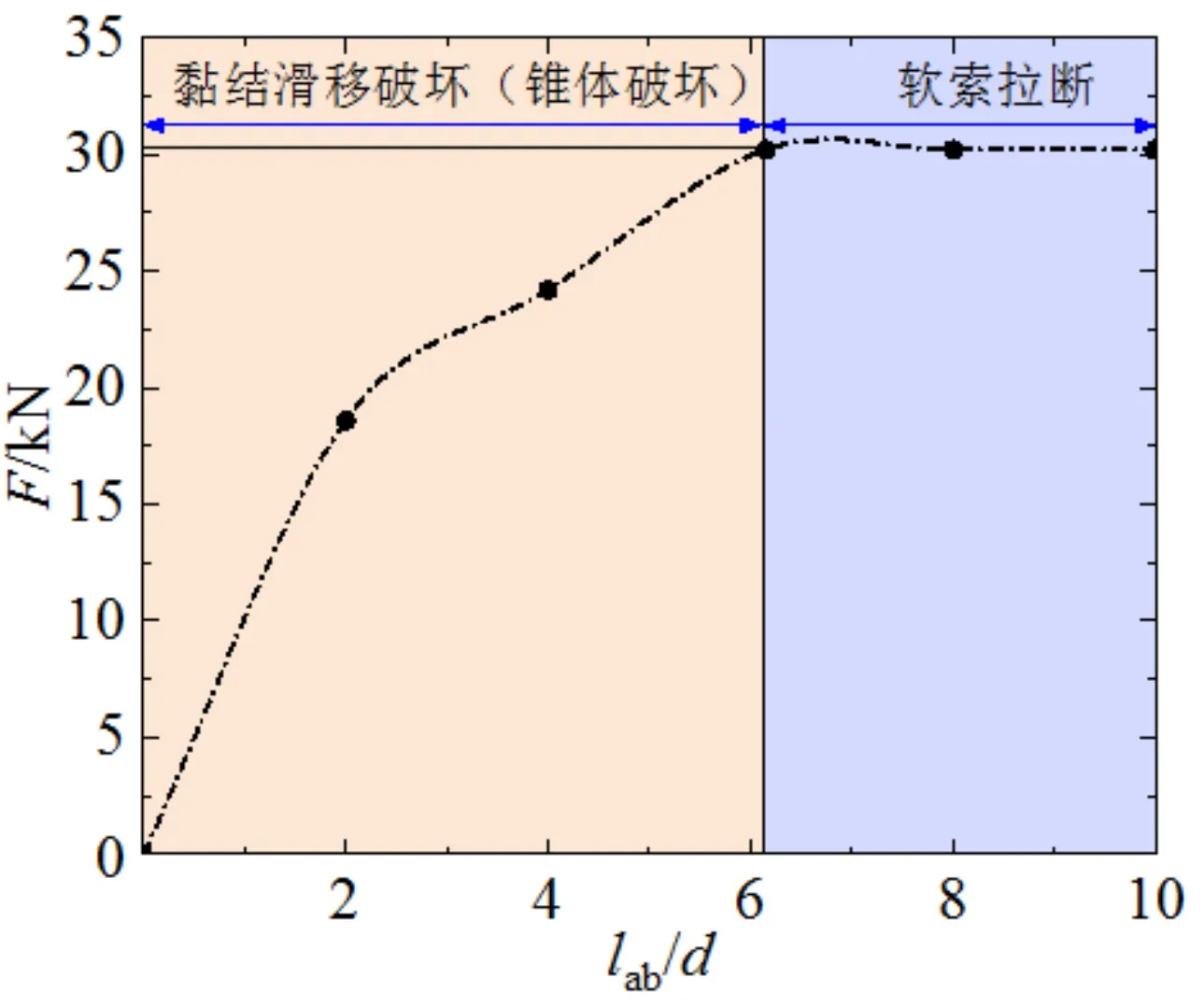
当试件SC2采用UHPC且钢绞线直径分别为4.5 mm和6.0 mm时,高强柔性索环不发生断裂的最大临界锚固长度分别约为6.2d和7.1d,且试件SC2在发生黏结滑移破坏时可能会发生混凝土锥体破坏,其荷载-锚固长度曲线如图9所示。

a d=4.5 mm

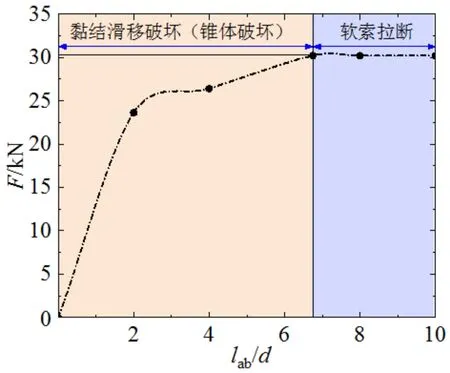
试件SC3荷载-锚固长度曲线如图10所示。当采用NC且高强柔性索环直径为4.5 mm时,高强柔性索环不发生断裂的最大临界锚固长度约为6.8d,且试件SC3在发生黏结滑移破坏时可能会发生混凝土锥体破坏。当采用NC且直径为6.0 mm时,高强柔性索环不发生断裂的最大临界锚固长度约为12.6d,且试件SC3在发生黏结滑移破坏时可能会发生混凝土锥体破坏,当锚固长度大于6.9d时,试件SC3可能会发生混凝土全截面破坏。

a d=4.5 mm

试件发生不同破坏形态时的临界锚固长度计算值如表2所示。由表2可知,UHPC、高强柔性索环和锚筋均可有效减少钢绞线的锚固长度,其中UHPC和锚筋的减少程度更为明显。以钢绞线直径为4.5 mm为例,当试件SC1和试件SC2均采用NC时,钢绞线和高强柔性索环发生黏结滑移破坏的最大临界锚固长度分别约为21.7d和20.5d,将材料类别由NC替换为UHPC后,钢绞线和高强柔性索环发生黏结滑移破坏的最大临界锚固长度分别约为10.8d和6.2d,分别减少了50.23%、69.77%。当试件材料类别分别为NC和UHPC时,与试件SC1相比,试件SC2发生黏结滑移破坏的最大临界锚固长度分别减少了5.53%、42.59%。当材料类别为NC时,试件SC3发生黏结滑移破坏的最大临界锚固长度约为6.8d,比试件SC2减少了约66.83%。

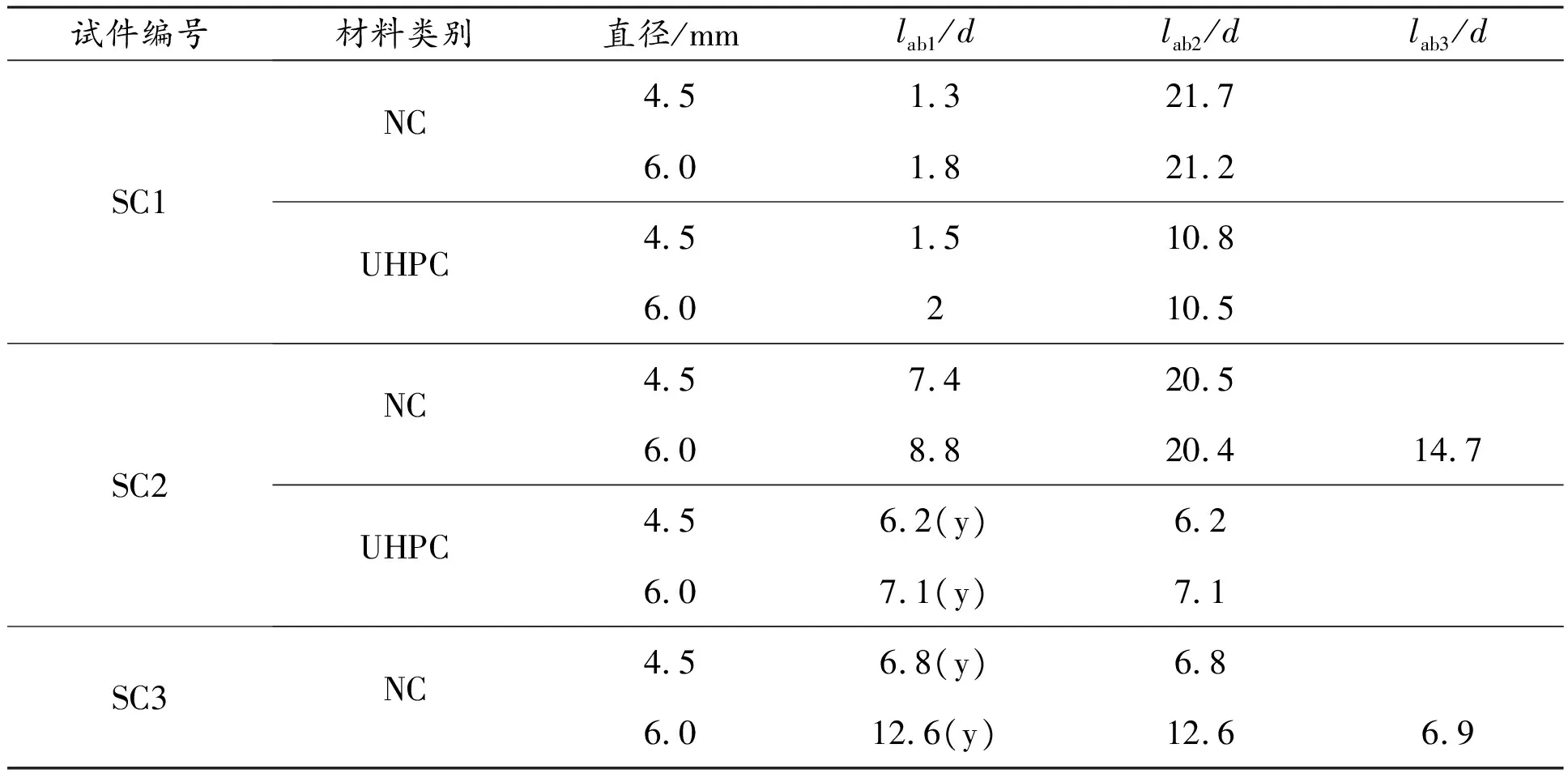
表2 临界锚固长度计算值

以直径为6.0 mm的钢绞线为例,分析试件发生锥体破坏和混凝土全截面破坏的临界锚固长度。当采用NC和UHPC时,试件SC1发生锥体破坏的最大临界锚固长度分别约为1.8d和2.0d,试件SC2发生锥体破坏的最大临界锚固长度分别约为8.8d和7.1d。结果表明,当试件SC2采用UHPC时,高强柔性索环在断裂前,可能发生锥体破坏。由表2可知,试件SC3采用NC和锚筋时,高强柔性索环在断裂前,也可能发生锥体破坏。此外,当试件SC2、试件SC3均采用NC,锚固长度分别大于14.7d、6.9d,且发生黏结滑移破坏时,可能会发生混凝土全截面破坏。

综上所述,高强柔性索环与UHPC具有良好的黏结锚固性能,在轴向拉伸荷载作用下,高强柔性索环与UHPC发生黏结滑移破坏的最大临界锚固长度理论值可减少6.2d。

5 结语

(1)提出了高强柔性索环分别与NC、UHPC在轴向拉伸荷载作用下发生不同破坏形态的理论计算方法,并给出了试件发生混凝土锥体破坏、黏结滑移破坏、混凝土全截面破坏和高强柔性索环断裂的临界锚固长度。

(2)UHPC、高强柔性索环和锚筋均可有效减少钢绞线的锚固长度,其中UHPC和锚筋的减少程度更为明显。当钢绞线直径为4.5 mm,材料类别由NC替换为UHPC后,钢绞线和高强柔性索环发生黏结滑移破坏的最大临界锚固长度分别约为10.8d、6.2d,分别减少了50.23%、69.77%。

(3)当高强柔性索环采用UHPC时,高强柔性索环在断裂前可能发生混凝土锥体破坏。当高强柔性索环直径为6 mm、采用NC,且高强柔性索环锚固长度大于14.7d时,可能发生混凝土全截面破坏。布置锚筋后,试件发生混凝土全截面破坏的锚固长度减小至6.9d。

(4)本文虽提出了高强柔性索环在NC、UHPC中的临界锚固长度计算方法,但考虑到NC、UHPC以及钢绞线的实际材料性能和物理参数等,尚需开展试验进一步完善和修正该理论计算方法。