基于加权最小二乘估计的电力系统故障定位方法

邹佳君

(国网吉林省电力有限公司,吉林 长春 130000)

0 引言

分布式发电、微电网、新一代电源、负载及设备在现有电力系统网络中的日益普及,对传统的电力系统保护方案提出了新的挑战[1-3]。为了能够对电力系统故障做出快速、准确的反应,在开始恢复作业之前,操作人员必须正确地掌握故障点和故障现象。然而,在现有的电力系统中运行的自动化系统对故障状态往往无法进行准确的识别,仍需依赖于操作人员的努力和判断[4]。虽然电力系统故障诊断是基于系统运行数据(包括保护继电器和断路器操作)的特定组合,但由于可能的组合几乎是无限的,且有多种判断标准,因此很难在传统计算机系统上使用逻辑程序实现这些判断[5]。针对现有故障定位算法的不足,本文提出了一种新的输电线路故障定位算法。

1 电力系统故障定位方法概述

从电力网络出现至今,电力系统中的故障定位问题一直是研究人员关注的重要问题之一。准确的故障定位,能够在电力系统发生故障的情况下,减少维修时间,从而提高电力系统的可靠性。相量测量装置(Phasor Measurement Unit, PMU)相关技术的日趋成熟,使电力系统的监测、分析及故障定位得到了迅速的发展。基于PMU的故障定位方法被称为广域故障定位(Wide-area Fault Location, WAFL),该方法通过处理电力系统不同位置测量的电压和电流相位来确定故障位置。WAFL方法可以分为:基于电压相量、基于电流相量以及同时基于电压和电流相量的3种方法。此外,非对称故障、非对称线路、不良数据、测量固有误差和线路阻抗误差等电力系统的实际情况是影响传输线故障定位算法精度的主要因素。到目前为止,这些因素在大多数研究工作中受到的关注相对较少。

2 基于电力系统的三相网络模型

尽管在过去的几十年里,有关电力系统故障定位的研究已经取得了许多成就,但仍然存在一些重要的问题,主要包括如下几个方面。

(1)用电力互感器和测量装置(如PMU)提取电量的过程称为测量链。错误的数据和测量链的固有误差进一步导致了故障位置估计的误差。每条测量链由互感器和PMU等测量装置组成。因此,两个分量的精度决定了测量误差的大小。而测量误差反映在电压和电流信号的幅值和相位角上,这些信号被用作故障定位算法的输入。

(2)故障定位算法的其他输入是输电网络参数。线路阻抗的准确性取决于所需计算的线路阻抗精度所需数据的可用性,环境条件相对于标准条件的变化以及线路导体的耗尽和老化。这些因素会导致传输线阻抗误差甚至高达30%。

(3)电力系统中最常见的故障是不对称故障。由于缺乏线路换位,大部分的电力系统传输线路也是不对称的,这增加了电力系统故障的难度。

针对上述问题,本文提出了一种新的加权最小二乘的故障定位方法。该方法采用故障点处三相电压的大小、角度以及故障点与故障线两端之间故障线段的阻抗对未知变量向量进行扩维,具有减小测量误差和参数误差、处理非对称传输故障以及开发所有故障分析算法的集成方案的潜在优势。同时,考虑非对称输电网络中发生的不平衡故障,该方法采用三相网络模型。在母线i和j之间连接的非对称传输线的三相模型如图1所示,其中包括相位的自阻抗和不同相位之间的互阻抗。通常,自阻抗和互阻抗是不同的。因此,i和j母线之间的三相传输线的串联阻抗矩阵为:

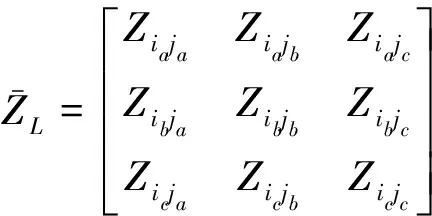
(1)

其中,Ziaja、Zibjb和Zicjc分别表示a、b和c相的自阻抗,其他元素表示其互阻抗。为了模拟传输线的分流导纳,将它们加到矩阵主对角线上的相应元素上,即:

(2)

其中,YCi和YCj分别表示i和j母线的并联导纳。电路的导纳矩阵是由输电线路和变压器的节点方程组成,用于构建电力系统的三相状态估计模型。

3 基于最小二乘的故障定位方法

三相状态估计方程涉及PMU测量,包括电压和电流相量到状态变量和网络模型参数。三相状态估计的输入是测量的电压、电流相量和由三相母线导纳矩阵表示的网络模型。一般而言,测量链的输出具有固有误差和偏置误差。传输线阻抗也存在影响母线导纳矩阵精度的误差。加权最小二乘是降低输入误差对电力系统状态估计结果影响的一种有效的求解方法。该方法通过分析测量残差向量来识别和消除不良数据。此外,通过误差协方差矩阵的正确设计,对测量链的固有误差进行了建模。加权最小二乘方法在不良数据检测方面的能力还可以用于故障发生的检测、故障线路的区分、故障类型和故障相位的识别。

式(3)为三相状态估计公式正常运行条件下非对称三相网络的分析框架。

(3)

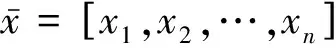
(4)

(5)

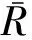
(6)

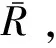
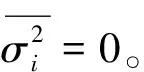
(7)

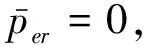
本文通过IEEE测试系统对所提方法的性能进行了研究。由于这些系统的传输网络是固有的对称网络,为了证明所提方法的能力,首先将对称网络转换为非对称网络。使用PowerFactory仿真进行故障模拟,并假设所有PMU都相同,没有测量信道限制。然后计算故障定位算法的相对误差。如图2所示,实验结果表明,基于故障电阻的故障定位估计误差,利用本算法给出了可接受的故障电阻达到100 Ω的结果,并且小于最大可接受误差1%的基线。

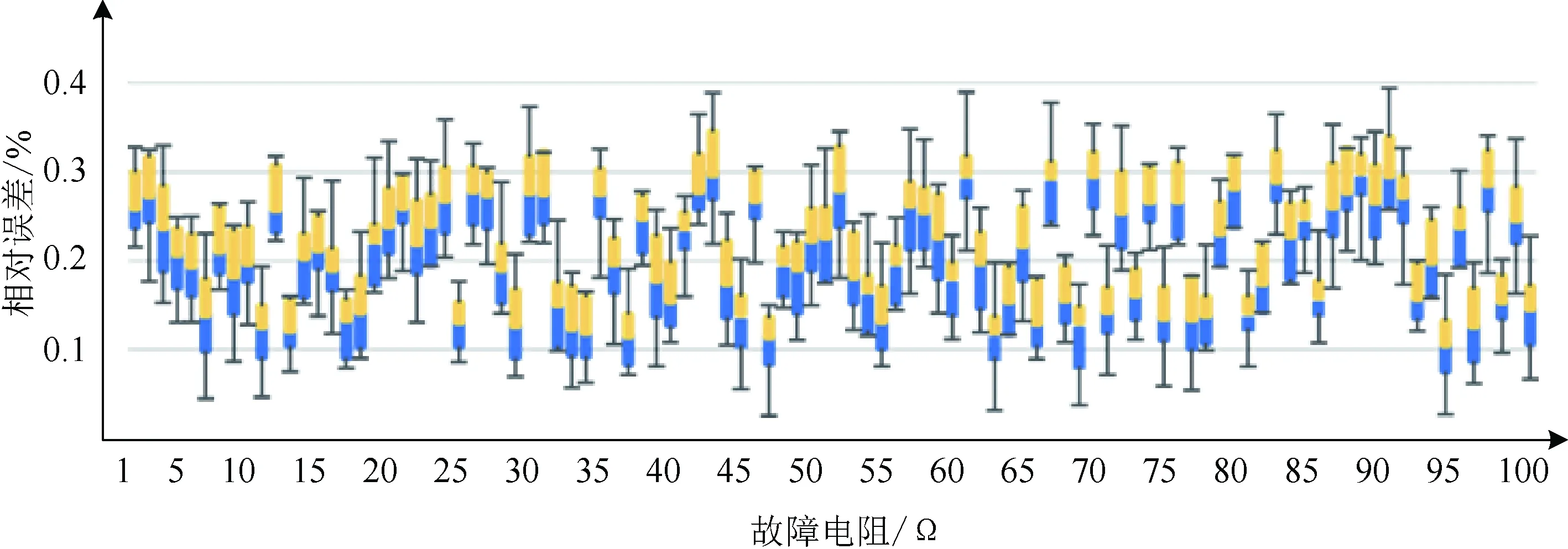
图2 不同故障电阻对应的误差

4 结语

本文针对电力系统的故障定位方法展开研究,提出将故障过程中测量到的电压和电流相量作为三相状态估计公式的输入,进行故障线路的判别和故障位置的计算。本文提出的基于最小二乘的三相状态估计方法能够兼顾非对称故障和非对称网络,检测和消除测量误差。因此,根据所提出的求解算法求解已定义的优化问题,可以准确估计电力系统状态、从而实现故障定位。实验结果验证了算法的有效性。