AEUR：基于uBlock 轮函数的认证加密算法设计

杨亚涛，董辉，刘建韬，张艳硕

（1.北京电子科技学院电子与通信工程系，北京 100070；2.西安电子科技大学通信工程学院，陕西 西安 710071）

0 引言

认证加密（AE,authenticated encryption）算法在信息保护领域作用重大，能够兼顾数据的机密性和完整性。通过将消息认证码和加解密算法结合，可以实现认证标签的单向计算过程，且在加解密环节拥有足够的安全强度，以抵抗常见的密码分析。

目前，主流的基于分组密码的认证加密算法主要有2 种设计方式：一是基于分组密码的认证加密方式，二是在现有的分组密码的基础上进行设计。前者依靠设计可靠模式结构并在底层使用分组密码算法为相关的加解密和认证验证提供服务，但提供服务的过程是不可见的，底层的算法可以相对简单地进行替换，这类典型的认证加密算法有OCB[1]（offset codebook）、EAX[2]（encryption with authentication for transfer）、GCM[3（]galois/counter mode）。

随着物联网等信息产业的迅速发展，认证加密算法的需求环境也发生了很大的变化，之前的通用算法和基于分组密码的工作方式类在现有的资源受限环境下的表现不尽如人意，如RFID（radio frequency identification）环境。直接设计类认证加密算法是指采用已验证安全性和其他性能指标的、成型的分组密码部件来进行认证加密算法的设计。这种设计方式致力于降低算法的实现代价和提升软硬件表现，因其采用消息来更新算法的状态，用于消息认证的实现代价较低。但这些算法的安全性不能通过可证明安全理论来证明，需依靠各种安全性分析方法，常见的此类型的认证加密算法有AEGIS[4]、ALE（authenticated lightweight encryption）[5]、AEZ（advanced encryption standard-easy）[6]等。为获得更好的认证加密效率与安全性，本文提出了新的方案。

本文的贡献如下。

1) 本文提出了一种认证加密算法通用结构R(t,s)。不同于已有采用AES（advanced encryption standard）轮函数的直接设计类认证加密算法，该结构基于轻量级分组密码算法uBlock[7]设计，以抵抗内部碰撞攻击为安全性目标，使用了混合整数线性规划（MILP,mixed integer linear programming）[8]方法，搜索确定结构中关键参数t、s和算法所使用的置换P，保证该结构在10 轮后有不少于66 个活跃S 盒。

2) 基于通用结构R(t,s)设计了认证加密算法AEUR（authenticated encryption algorithm based on uBlock round function）。AEUR 算法的设计基于uBlock 轮函数和广义Feistel 结构，以4 个uBlock轮函数和置换P组成了算法的轮函数，轮函数用来更新状态值，状态值保证算法的正确性。算法处理数据的过程简洁有效，从而优化了算法运行过程，减少了资源消耗。AEUR 算法对多种安全性分析方法具有充分的抵抗能力，为国产密码算法应用提供了一条新的参考途径。

3) 应用SSE（streaming SIMD extension）指令集[9]对AEUR 算法进行了软件实现。对AEUR 算法进行实现速率测试，以软件运行时间计算，AEUR算法相比其他同类算法在运算速度上均有不同程度的提升，具有较好的综合性能。

1 相关研究

Bellare 等[10]在ASIACRYPT 2000 上提出了认证加密这一全新概念，将认证和加解密在同一算法中完成，通过共享一个密钥来实现数据的机密性与完整性。近年来，部分学者拓宽了认证加密算法的应用领域，并基于不同的经典密码算法实现了新的认证加密方式。2002 年，Rogaway[11]提出了基于相关数据的认证加密（ADAE,associated-data authenticated encryption）算法，结合OCB 和伪随机函数PMAC（parallelizable MAC）构造了ADAE 算法，这种认证方式在保证了明文信息的保密性和完整性同时也保证了相关数据的完整性。2008 年，Iwata[12]提出了一种针对区块密码的认证加密模式，其中加密部分由一个CENC（common encryption）的密钥流生成，并结合了基于分组密码的哈希函数。2010 年，Sarkar[13]提出了并行认证加密模式，并与IPMAC（improved parallelizable MAC）结合，获得新的认证加密方案。

随着对认证加密领域以及应用环境的不断研究和探索，原有的认证加密方案设计思路不能很好地适应新的应用环境。同时，基于新结构和新思想的方案不断被提出。CAESAR（competition for authenticated encryption: security,applicability,and robustness）竞赛的举办大大推动了认证加密算法设计的发展，其第三轮算法的特点介绍[1,4,14-16]如表1 所示。

表1 CAESAR 竞赛第三轮算法特点

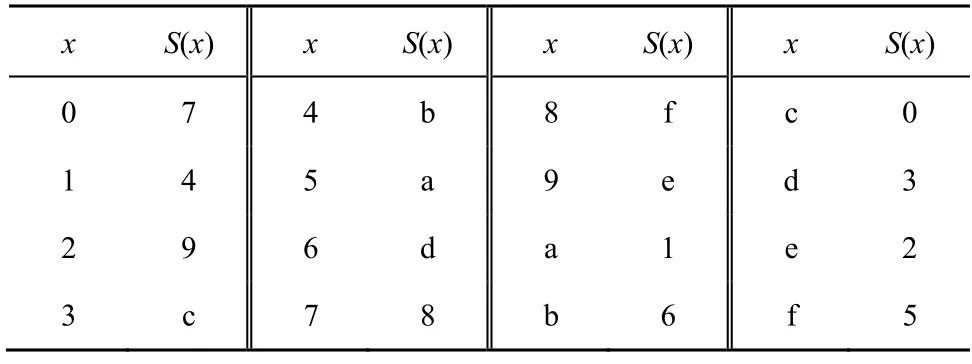
表2 uBlock 算法S 盒

表3 PL128 和PR128 变换参数

2018 年，张建等[17]基于SM4 轮函数设计了认证加密算法SMAE，该算法利用MILP 方法构造了消息认证码和认证加密算法。2020 年，高国强等[18]基于AES 算法底层的轮函数，实现了一种基于AES 轮函数的认证加密算法AMRAE。这2 种算法都是基于现有的分组密码轮函数来设计的，但安全性分析与实现效率尚有不足。本文综合前述经验，分析了现有方案的不足，在上述学者的研究思路上进行了扩充改进，采用2019 年我国第一届密码算法设计竞赛中获得一等奖的分组密码算法uBlock 设计认证加密算法AEUR，其在安全性和实现速率方面较SMAE 和AMRAE均有不同程度的提升，为国产认证加密算法提供了一种新的参考。

2 基础知识

2.1 uBlock 轮函数

uBlock 算法[7]的分组和密钥长度为128 bit 和256 bit，记为uBlock-128/128、uBlock-128/256、uBlock-256/256。本文采用uBlock-128/128。

uBlock 算法对差分分析、线性分析、积分分析、不可能差分分析等密码分析方法都有相应的安全冗余。uBlock 算法的密钥扩展算法可以通过随用随生成的方法得到轮密钥，这样能够减少算法需要的存储空间。在本文中，＜＜＜b表示循环左移bbit，表示以32 bit 为单位循环左移bbit。

图1 uBlock 算法轮函数

2.2 混合整数线性规划

MILP[8]是在一定约束的条件下对目标函数进行优化，遵循线性规划的优化问题方法。用MILP 方法对密码算法进行差分分析和线性分析，就是通过设定相应的约束条件，将活跃S 盒的个数之和最小设定为目标函数，并对其求解。

依据S 盒的相关特性结合约束条件，再将最小活跃S 盒的数量作为目标函数的构造条件，设计目标函数的数值即所求的最小值。完成上述构造后，就可以用求解器对此MILP 问题进行求解。此外，当输入阶段差分和临时变量都被设为0 或1 时，对于求解器的求解速率更加友好[19]。

3 基于uBlock 轮函数的通用结构设计

R(t,s)结构以uBlock 算法轮函数和广义Feistel结构为基础，其安全性目标为在密钥长度为128 bit时，可以抵抗内部碰撞攻击。其构建过程采用了MILP 方法，搜索符合安全性目标的结构参数t、s和置换P，其中，t为uBlock 算法的执行次数，s为轮函数输入信息的长度，长度表示消息的块数。

3.1 安全目标

因为R(t,s)是基于分组密码算法轮函数和分组密码算法结构所设计的通用结构，不具备算法的完整性，从算法分析的角度来看，可以从某些分析方法的角度来设定其安全性目标。在AEUR 算法通用结构的设计中，主要考虑的是对内部碰撞攻击的防御。碰撞攻击[20]利用生日悖论，分析算法本身或其等效结构，结合与轮密钥之间的对应关系来获得区分属性，继而分析得到密钥信息。碰撞攻击大大减少了原始穷举攻击的计算量。对于R(t,s)结构，当存在2 个不同消息的差分时，引入初始差分，经过多轮迭代，内部状态差分为0。R(t,s)的密钥为128 bit，当攻击复杂度大于128 bit 时，对该结构的攻击是无效的。uBlock 算法使用的4 bit S 盒的最大差分概率[7]为2-2，为满足上述安全性条件，在进行碰撞攻击时活跃S 盒的个数不能少于66 个。

3.2 通用结构R(t,s)

R(t,s)结构是一种通用的、可迭代的认证加密算法轮函数结构，采用uBlock 算法的轮函数，结合广义Feistel 结构，如图2 所示。置换P是区别于uBlock轮函数的向量置换PLn和PRn的新的置换，表示消息，S0～S7表示状态值。MesHandl 为消息Fi与状态值分别进行异或运算。

图2 R(t,s)轮函数结构

定义1要对结构R(t,s)的效率进行计量，需要确定一个指标即处理32 bit 的消息块需要的uBlock 轮函数的个数。

R(t,s)的效率与rate 相关性强，需要通过对结构的设计细节进行研究，以选取更高效率的结构。

3.3 MILP 模型搜索实验结果

假设置换P基于32 bit，给出t、s和相应约束，结合MILP 方法验证是否找到符合条件的置换P。

当rate=1 时，存在只有一个活跃S 盒的差分路径使结构发生内部碰撞[17]。下面证明rate 至少为2时结构R(t,s)才可能避免内部碰撞。在搜索了t=1 和t=2 的4!和8!个置换后，发现并没有符合安全目标的结构；当t=3 时，开始出现满足结构安全的轮函数。对于R(3,1)，找到了多个可用的P，如P=(1,2,3,4,5,6,7,8,9,10,11,0），此时P被设为一个循环移位，进行10 轮后，活跃S 盒的个数达到70，满足安全性目标，但其rate=3，需要寻找效率值更高的P。在对R(3,2)、R(3,3)、R(4,1)、R(4,2)、R(4,3)、R(4,4)进行搜索后发现，以上结构均存在满足安全性目标的P，其中R(3,3)、R(4,4)的rate=1，效率较高。但是R(3,3)的算法全扩散轮数表现弱于R(4,4)，故选择R(4,4)[18]。

表4 列出了部分使R(4,4)符合安全性目标的置换P及其活跃S 盒个数。在满足安全性目标的前提下，综合各个结构的实现效率，P5的实现效率和安全性均能够达到通用结构对认证加密算法实现的要求，其扩散和混淆特性也满足作为认证加密算法部件的要求，经验证P5的综合性能优于其他置换P，故本文方案选取P5作为通用结构的置换P。

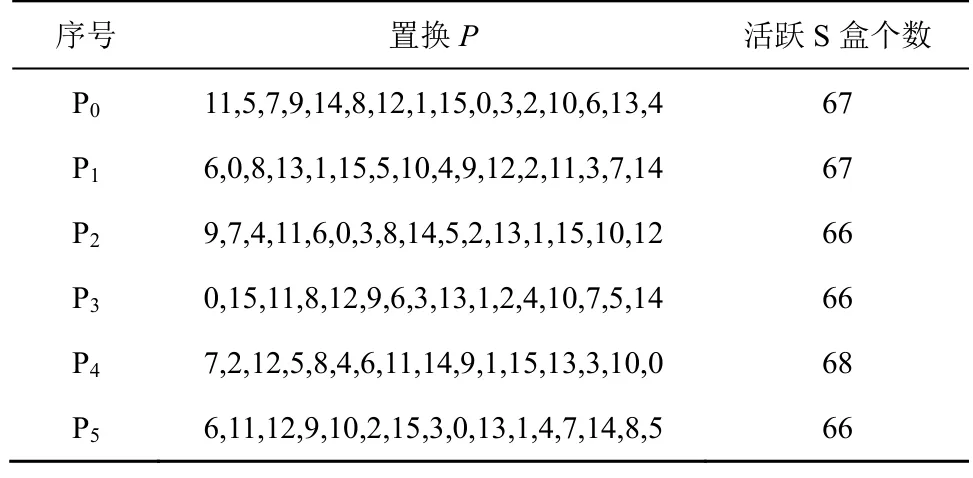
表4 部分使R(4,4)符合安全性目标的置换P及其活跃S 盒个数

3.4 通用结构R(4,4)差分安全性分析

R(4,4)结构的安全目标是抵抗内部碰撞攻击。考虑到该结构作为认证加密算法的主要部件，其安全性需要从更多方面进行检验，可以通过差分分析来实现。

差分分析针对明文差分对和相应的密文差分，尽可能地获得更多的密钥信息。对于R(4,4)结构，建立MILP 差分模型，搜索该结构的高概率差分路径，该结构中存在异或和移位2 种线性操作。在构建差分模型过程中，移位只是单纯地改变了差分值的位置，所以不需要进行多余限制。对于比特异或a⊕b=c，可以采用等式 △a+△b+△c=2d[21]结合R(4,4)结构的差分性质来求解，过程中还需利用MILP 进行约束，并用Gurobi 求解器求解。

按照R(4,4)结构进行差分路径分析，在每一轮都选取差分值与上一轮差分值相同的差分，构成差分路径，最终求得一条长度和精确度符合要求的差分路径概率。搜索结果如表5 所示。

表5 R(4,4)结构差分路径概率

从上述结果可知，当R(4,4)结构执行9 轮时，差分路径概率为2-152，满足设定的差分复杂度安全目标128 bit，因此R(4,4)结构从理论上可以抵抗差分分析，且不存在可行的差分路径。

4 认证加密算法AEUR 设计

AEUR 算法主要考虑底层算法的选取原则、通用结构设计和整体工作流程与安全性3 个方面。

首先，对于底层算法uBlock，主要关注其轻量级的设计思路和随用随生成的密钥扩展算法，且能够抵抗内部碰撞攻击。其次，对于通用结构R(t,s)的设计，主要关注其安全性目标和使用MILP 方法搜索时的参数结果，且R(t,s)结构可以根据底层算法的安全性需求和运行特点，选择不同的置换P和底层轮函数个数，适用性广泛。最后，对于整体认证加密算法工作流程，主要考虑其认证加密过程和解密过程中对消息数据处理的运算效率和正确性。AEUR 算法的设计思路如图3 所示。

图3 AEUR 算法的设计思路

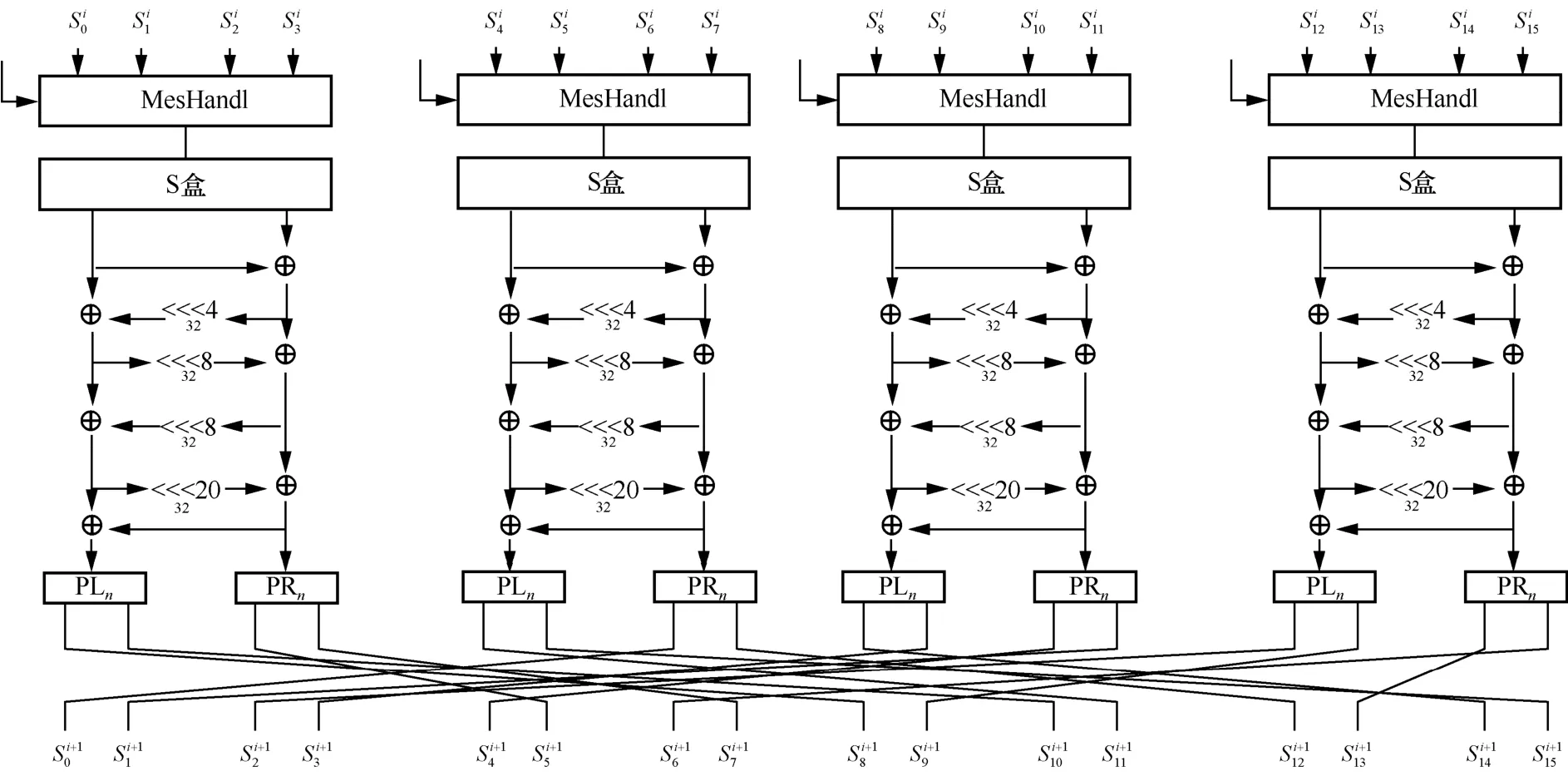
图4 AEUR 算法的轮函数结构

AEUR 算法采用R(4,4)作为轮函数，密钥、初始向量和随机常数作为状态值的初值，利用轮函数进行状态值的更新，利用状态值对数据进行加解密和生成标签操作。

4.1 AEUR 算法认证加密过程

1) 初始化

首先进行相关数据与明文的填充。本文使用PKCS5 算法进行数据填充。PKCS7 算法是目前常用加密算法都遵循的数据填充标准，PKCS5 算法作为PKCS7 算法的子集算法，在数据块大小blockSize 上固定为128 bit，即数据始终会被切割为128 bit 的数据块。然后计算需要填充的长度，由需要填充的字节数目来决定要填充的内容。此外，为了解决加解密时对于数据填充的处理问题，当数据本身长度满足128nbit 时，依据PKCS5 的规则，在数据的尾部仍需要填充8 个字节的内容，此时填充内容为0x08。

将k和N赋值到状态值中，并利用轮函数更新16 轮状态值，再对相关数据进行初始化，如算法1所示。

算法1AEUR 算法初始化

2) 明文信息的处理

将明文信息填充后按32 bit 分块，利用状态值与明文异或来生成密文，之后明文进行状态值更新，重复q-1 轮。具体算法过程如算法2 所示。

算法2AEUR 算法明文信息处理

输入明文M

3) 标签的生成

首先利用相关数据和消息长度adlen 和msglen更新一轮状态值；然后迭代更新16 轮；最后利用状态值生成标签tag。具体过程如算法3 所示。

算法3AEUR 算法标签生成

4.2 AEUR 解密认证过程

AEUR 的解密认证算法输入为密钥k、初始向量N、相关数据A和密文C；输出为明文M或停止符⊥，认证解密过程由初始化、密文信息处理和标签生成过程构成。

解密认证过程的初始化、密文信息处理与加密认证过程的输入输出相同。最后生成状态S16+d。

解密过程。利用状态S16+d和密文C=(C0,…,C4q-1)生成M，同时更新状态。具体算法如算法4所示。

算法4AEUR 算法密文信息处理

认证过程。在解密过程结束后可以得到状态值S16+d+q，之后利用加密认证过程中的标签生成算法，得到标签tag′，如果标签值tag′与之前加密认证过程中生成的标签值tag 相同，那么解密成功且通过认证，即解密验证算法执行成功，输出明文M；否则解密验证过程失败，输出停止符⊥。

4.3 基于通用结构R(t,s)的认证加密算法设计思路

R(t,s)结构是能够满足不同算法使用的通用型迭代结构，满足分组密码算法要求的混淆和扩散特性，且可以保障认证加密算法的安全性和正确性。采用这种结构生成的认证加密算法总体类似于大型序列密码算法。该结构通过并行操作可以大大提升运行效率，根据底层算法的安全性需求和运行特点，可以选择不同的置换P和底层轮函数个数，从而构造出满足安全性和实用性要求的结构，继而将其进行组合排列，满足算法的设计需求。

5 正确性证明

加密认证和解密验证使用了相同的初始化、明/密文信息处理和标签生成过程，如算法5 和算法6 所示。

算法5AEUR 算法加密过程

算法6AEUR 算法解密过程

由于算法的加解密与状态值紧密相关，如果在任意某一轮数时，算法在加解密过程中产生的状态值Si相同，则算法满足正确性。执行AEUR 算法时，其加密与解密的初始化过程、相关数据处理过程完全一致，每一轮产生的状态值都相同，因此AEUR 算法满足正确性。

6 安全性分析

现有的可证明安全理论虽然可以对基于分组密码的认证加密模式进行安全性分析，但对于直接设计的认证加密算法，不能给出适合的安全假设。目前，直接设计的认证加密算法普遍使用针对密码算法的安全性分析方法[22]。为了让AEUR 算法具备能够抵抗密钥恢复攻击和伪造攻击的能力，保证攻击的复杂度大于2128，做出如下约束[18]。

1) 初始向量值（Nonce）的取值要随机，且不能复用，即每次使用认证加密算法之前都要更换随机初始向量值。

2) 在解密验证的过程中，明文信息对用户不可见，只有在验证成功后才会输出明文；如果验证失败，则输出停止符⊥。

3) 加密时，相同密钥对相关数据和明文信息加密的最大数据长度不超过2128bit。

6.1 AEUR 算法安全性分析

1) 线性攻击

线性攻击[23]是一种已知明文攻击，也就是攻击者能够获取当下使用密钥状态下的明密文对。在对明文、密文和密钥三者满足的某种线性关系的概率p进行研究后，得到一个统计特征，利用该特征能够将分组密码和随机置换区分开。对分组密码而言，期待找到一个线性区分器来恢复最后一轮密钥。采用MILP 方法构建目标函数和约束条件来搜索其最小活跃S 盒，设置活跃S 盒的下界，从准确度考虑，将搜索过程中每一轮的S 盒个数进行输出，结果如表6 所示。在线性攻击的标准方法评估下，AEUR 算法的10 轮活跃S 盒下界为71，大于安全性目标设定的66 个。且AEUR 算法在标签生成和初始化阶段均使用了16 轮迭代，有足够的安全冗余，所以其具有抵抗线性攻击的能力。

表6 AEUR 算法在线性攻击条件下的活跃S 盒个数

2) 滑动攻击

滑动攻击[24]是受相关密钥攻击的启发而提出的。当分组密码在迭代过程中出现一定的自相似性时，可以使用滑动攻击对算法进行分析。与线性或者差分攻击不同，迭代轮函数的性质和执行轮数对滑动攻击的影响很小，轮数对算法抵抗滑动攻击的能力几乎没有影响。在密码算法中，如果迭代函数可以被分解为若干小的轮函数，那么就可以利用这一缺点进行滑动攻击。为了避免滑动攻击，算法的轮函数，特别是迭代的轮函数应该避免在执行过程中形成周期而被分解，在综合考虑算法抵抗几种攻击方法的能力以及对运行效率的影响后，与文献[18]的分析相同，AEUR 算法的轮函数并未生成周期，因此AEUR 算法可以抵抗滑动攻击。

3) 猜测确定攻击

猜测确定攻击[25]的原理是对密码算法实现过程中的一些变量进行猜测，猜测的变量在轮函数中迭代可得到新的变量，利用得到的变量恢复出算法实现过程中相应的状态值。AEUR 算法的扩散层来源于uBlock 算法，其扩散层的二元域矩阵分支数为8，攻击者需要已知64 bit 才能得到下一个字节变量的值。AEUR 算法轮函数是基于状态值集合Si构造的，有16 个32 bit 的状态值。那么对于AEUR 算法的猜测确定攻击，则需要以32 bit 的状态值进行攻击，为了满足算法的安全性目标，攻击复杂度最高临界值被设定为2128，显然想通过4 个变量来恢复其他的状态值并不现实，所以AEUR 算法可以抵抗猜测确定攻击。

4) 状态恢复攻击

Pelican MAC 攻击[26]主要利用小尺寸的内部状态来构造基于生日悖论的碰撞。AEGIS、ALE 算法都具有较大的内部状态，在AEUR 算法中，状态值Si的大小为16×32=512 bit，足以抵抗生日攻击。当攻击者使用相同的密钥和随机数进行多次重复攻击时，可能会在标签生成过程中对状态值注入差分，特别是当标签的长度小于算法的密钥长度时，认证加密算法面对这种攻击会显得脆弱。在AEUR算法中，轮函数结构的安全性目标为抵抗内部碰撞攻击，因此针对状态恢复攻击是不现实的。在多次攻击之后，可能获得相对成功的伪造，但无法恢复整个状态值。因此AEUR 算法可以抵抗状态恢复攻击。

5) 伪造攻击

伪造攻击是指攻击者伪造出通过验证的密文来进行攻击。R(4,4)在9 轮迭代情况下的差分路径概率为2-152，远超过设定的128 bit 安全性复杂度目标，因此，该结构能够抵抗差分分析，且无可用差分路径。AEUR 算法的结构与R(4,4)相同，且迭代轮数超过10 轮，拥有绝对安全冗余，无法实现伪造。因此，AEUR 可以抵抗伪造攻击。

AEUR 算法作为直接设计类认证加密算法，其底层算法uBlock 对差分分析和不可能差分分析等具有良好的抵抗性。R(t,s)结构可以抵抗差分分析和伪造攻击等，并以128 bit 的复杂度为安全性目标，保障结构的安全性。因此可以认为AEUR 算法对差分分析等方法也有足够的抵抗能力。

6.2 安全性对比分析

为了进一步说明AEUR 算法的安全性，选用近年来最有代表性的具有同类结构的AEGIS 算法、SMAE 算法和Pyjamask 算法[27]作为对比对象。

AEGIS 算法[4]在拒绝初始向量重用的情况下，在标签生成过程中，恢复密钥攻击的速度要慢于穷举搜索，因此状态恢复攻击对于拒绝Nonce重用的AEGIS 无法实施。在伪造攻击中，解密的明文若验证成功，当t为标签值tag 的长度时，有2-t的概率可以被攻击者破解。AEGIS 的标签长度为128 bit，在恢复状态时至少需要2128次伪造尝试，由计算复杂性理论可知，这一数值在计算上是不可接受的。因此，AEGIS 对状态恢复攻击和伪造攻击具有安全性。

SMAE 算法[17]就猜测确定攻击而言，因为其底层函数来源于SM4 算法，SM4 算法中线性变换L的分支数为5，即对于SMAE 算法而言，要想通过猜测确定攻击来分析算法，至少需要得到32 bit 的输出值，才能恢复新的字节值，同时考虑到算法的128 bit 的计算安全性指标，超过3×32 bit 的恢复状态攻击不可行，因此SMAE 算法对于抵抗猜测确定攻击具有安全性。在线性攻击分析中，计算搜索线性掩码成立的最优偏差为2-92.43，区分攻击和明文恢复攻击的数据复杂度约为2184，因此SAME 算法对于线性攻击具有安全性。

AEUR 算法对于多种攻击具有安全性，较SMAE[17]和AEGIS[4]更全面，对比细节如表7 所示。

表7 AEUR 算法和其他算法的安全性对比

2020 年，Goudarzi 等[27]提出了Pyjamask 算法并给出其规范和AEAD（authenticated encryption with associated data）建议。2022 年，贺水喻等[28]基于Pyjamask 算法提出一种对明文进行伪造的方法，可以伪造出认证标签。在对Pyjamask 和AEUR算法的AEAD 安全性进行对比分析时，两者均具有良好的认证加密安全性。AEAD 安全性要求算法具有保密性、真实性、对称性和随机分配的特点。

1) 在实际认证加密执行过程中，AEUR 算法能够抵抗线性攻击等多种攻击方法，密文解密后对应的明文正确，标签值对应正确。除了明文长度之外，其他关于明文的内容是未知的，满足保密性。

2) AEUR 由于R(t,s)结构，未经有效的密码分析检测，攻击者不可能更改密文的底层，满足真实性。

3) AEUR算法对各类明文进行加密和对各类密文进行解密时使用的密钥相同，满足对称性。

4) AEUR 算法的加密过程是随机分配的，同一明文的2 个消息会产生不同的密文，攻击者无法获知明文与密文的对应关系，满足随机分配性。

综上，AEUR 算法满足对称密码算法理想的AEAD 安全性。

7 效率与实现分析

本节使用C 语言结合SSE 指令集实现AEUR 算法。环境为Intel 处理器，16 GB 内存，Visual Studio 2019。AEUR 算法中的uBlock 轮函数采用SSE 实现。SSE指令集采用SIMD（single instruction multiple data）来提升数据的并行操作性和算法的实现效率。

将AEUR 算法的时间复杂度和空间复杂度与其他算法进行对比分析，结果如表8 所示。

表8 计算复杂度对比

由表8 可知，AEUR 算法的时间复杂度与SAME算法相同，优于AMRAE 算法[18]；AEUR 算法的空间复杂度与SMAE 算法相同，低于AMRAE 算法。参考AEUR 的存储开销和运行开销等，其综合性能良好。

AEUR 算法认证加密速率如图5 所示。从图5可以看出，AEUR 算法认证最高为5.41 Gbit/s，最低为3.91 Gbit/s，平均为4.63 Git/s，考虑到AEUR算法的运行环境，相比文献[17]中SMAE 算法3.8 Gbit/s 的加密速率，AEUR 算法认证加密速率对比SMAE 算法仍有较大优势。

图5 AEUR 算法认证加密速率

由表9 可知，AEUR 的认证加密速率相比AEGIS[4]、ALE[5]效率分别提升了3%和46%，相比AES-GCM[3]、ACORN[29]算法优势较明显，加密速率分别提升了74%和92%。

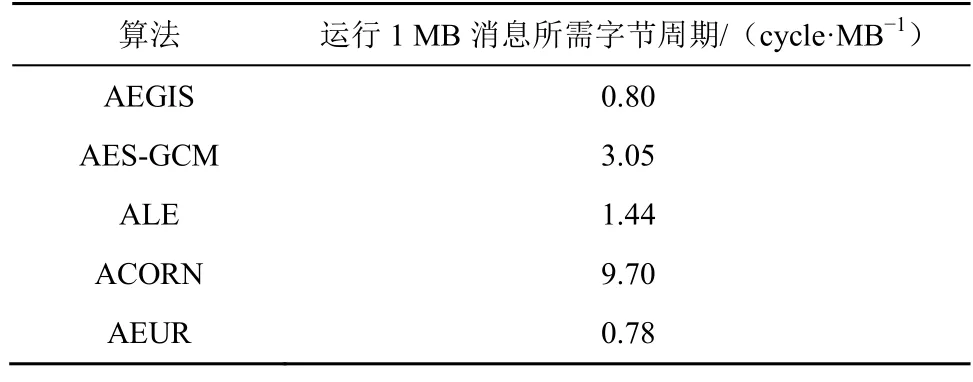
表9 算法速度比较

另外，通过测试不同数据长度的认证加密运算过程，可以得到如图6 所示的状态曲线。随着待处理数据长度的增加，AEUR 算法执行的效率较AEGIS 算法和AES-GCM 算法更加稳定。

图6 算法认证加密时间随数据长度变化

结合图5、图6 和表9 可以得出结论，AEUR算法与以AES 算法为基础设计的AEGIS 算法、ALE算法、AES-GCM 算法和以序列密码为基础设计的ACORN 算法相比，具有更优的运算性能。

通过上述对计算复杂度、认证加密速率和算法效率的对比分析可以看出，本文的AEUR 算法较其他认证加密算法具有技术优势。其原因一方面是AEUR 的底层结构是基于轻量级分组密码算法uBlock，uBlock 算法的密钥扩展算法可以通过随用随生成的方法得到轮密钥，在一定程度上缩小了存储空间，并且能够提升运算效率。而且所使用的MILP 方法可以根据所采用的分组密码算法S 盒的特性来设置约束条件，使其适用性得到增强。

另一方面是AEUR 算法的设计基于分组密码uBlock 的轮函数和广义Feistel 结构，以4 个uBlock轮函数和置换P组成了算法的轮函数，状态值的更新通过轮函数来完成，因此算法处理数据的过程在一定程度上得到了优化，也减少了资源消耗，从而降低了运算复杂度，提升了运算速率。

8 结束语

本文采用国产分组密码算法uBlock 轮函数结合混合整数线性规划方法，设计了一个适用于认证加密算法的通用迭代结构R(t,s)，并基于R(t,s)结构设计了认证加密算法AEUR。AEUR 算法由初始化、明文信息处理和生成标签过程构成。对算法的正确性与安全性进行分析，并与同类算法进行对比，AEUR 表现较好。使用C 语言结合SSE 指令集编码实现了AEUR 算法，测试了算法的软件实现效率。AEUR 算法与以AES 算法为基础设计的AEGIS 算法、ALE 算法、AES-GCM 算法和以SM4 算法为基础构造的SMAE 算法，以及以序列密码为基础设计的ACORN 算法相比，具有更优的实现性能。

随着口令认证加密技术的发展，该方向得到了广泛研究[30-31]，未来AEUR 算法可结合口令安全技术应用于物联网、隐私计算等领域。