基于梯度提升决策树的锅炉燃烧优化控制策略研究
肖 勇,马 乐,胡 波,王艺晴,毛 华
(西安热工研究院有限公司,陕西西安 710054)
锅炉燃烧控制系统的合理管控,对于提高燃烧效率、减少污染物排放及降低成本具有重要意义[1-3]。其中,超超临界的锅炉燃烧调整需要基于风煤比、煤水比与功煤比进行。但由于超超临界锅炉受到多种因素的影响,故其具有强耦合度及高非线性的特点,需要进行大量的反馈校正与基于经验的调整。换言之,只有当系统出现问题时才会进行校正,极大地降低了效率,并有可能影响调整效果。此外,若校正设置不合理,还会带来相反的结果,影响锅炉及周边设备的安全运行。因此,开展超超临界锅炉燃烧的最优化控制研究至关重要。
文中针对超超临界锅炉的最优化控制问题,引入了梯度提升决策树(Gradient Boosting Decision Tree,GBDT)技术,同时基于燃烧粒子模型建立了相关算法,并通过实验进行了验证。
1 锅炉燃烧模型
该研究中的锅炉模型由一组偏微分方程构成[4],这些方程描述了气态流体在反应炉中的时间及空间运动。此外,还使用了非均质模型,用于预测气固相之间的边界层厚度等重要属性。
该文设计的锅炉燃烧模型考虑的假设如下:
1)反应粒子被建模为完美的球形粒子;
2)反应粒子具有恒定的体积;
3)反应粒子颗粒具有宏观上均匀的结构,且不受反应的影响;
4)反应粒子颗粒内金属氧化物分布均匀;
5)反应器内的反应粒子分布均匀。
图1 为反应炉示意图,其说明了反应器模型与反应粒子模型在边界条件下的相互作用。在此基础上,建立反应器和反应粒子的质量及热平衡方程。
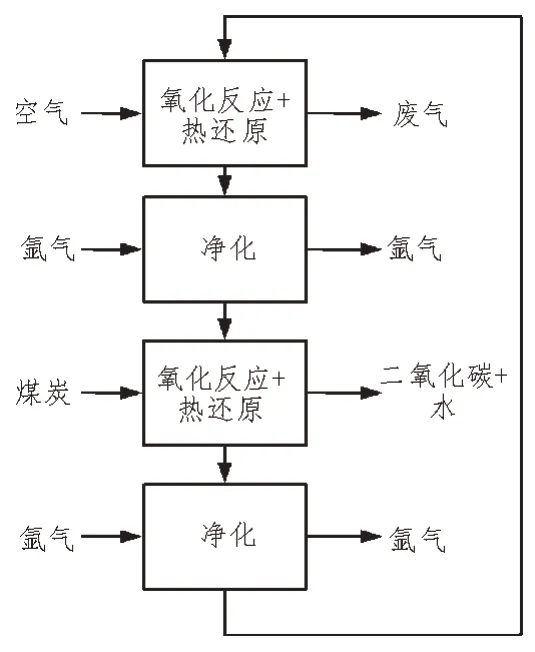
图1 反应器示意图
填充床反应器的质量和能量平衡公式如下:
式中,Ci,j为阶段j的初始浓度,Fi,j为气体种类的摩尔流量,Daxi,j为第j阶段物种i的轴向色散系数,x和z表示反应器的两个方向,t为时间,V为流速。εb、Ac、kci,j和av为对应标量参数,Tcj和Tj分别表示入口及反应中的温度[5]。同样,体相的边界条件如下:
式中,yifeedj为进料中第i种物质的摩尔分数,Finj为入口处气体种类i的摩尔流量,Ac为直管截面积,Cpjj为反应粒子在阶段j的热容量,ρin,j为j阶段气体混合物的热导率,εb和λaxj是对应的标量参数。
在反应器的质量与能量平衡方程中,轴向位置由z(0≤z≤L)表示,L为反应器的长度。类似地,时间变化表示为t(0≤t≤tj,final),其中tj,final表示反应中每个阶段j的批处理时间。此外,Tj(z,t)表示反应过程中每个阶段在空间及时间域上的温度分布。式(1)-(2)明确考虑了反应器体相与位于反应器中轴向位置z的反应粒子颗粒间的对流、轴向扩散、质量和热传递;式(3)-(4)表述的边界条件,分别描述了反应器入口处的质量和热量进料流条件;式(5)则描述了反应器出口流的质量与隔热条件,而方程式(6)描述了每个阶段j的入口质量通量。
反应粒子的质量和能量平衡公式如下:
粒子相所需的边界条件如下:
式中,粒子的径向位置由rc(0≤rc≤Rp)表示;Rp表示粒子的半径;Ci,j(z,r,t)表示粒子径向和时间域中在每个阶段j时气体种类i的浓度,而Tcj(z,r,t)则表示反应过程中每个阶段j的粒子温度曲线。式(7)-(8)所示的粒子模型明确考虑了径向扩散。式(9)则描述了反应粒子中心的质量及隔热条件,并在此基础上使用方程(7)-(8)中的Ri,j描述反应过程的动力学项。
2 基于梯度决策树的优化控制
该文在建立了锅炉燃烧反应模型的基础上,使用梯度提升决策树研究锅炉燃烧的优化策略[6]。其中,XGBoosting(Extreme Gradient Boosting)是最常用的梯度决策树算法之一。当决策树在此过程中生长时,XGBoosting 通过计算方差增益来执行拆分[7]。例如,令O为决策树固定节点上的训练集,则该节点在节点d处分裂特征j的方差增益可表示为:
对于特征j,梯度决策树算法选择=arg maxdVj(d)并计算最大增益[8-9]。然后根据特征j∗在点dj处将数据拆分为左右子节点。大多数梯度决策树学习算法如该文使用的XGBoosting 均是按层次生长树,这意味着在每个集成时间步长,最深层次的所有节点均会增长。
LightGBM(Light Gradient Boosting Machine)是微软开发的开源梯度提升决策算法软件[10-11]。其使用基于直方图的算法来加快训练过程、减少内存消耗,同时结合先进的网络通信来优化并行学习,故被称为并行梯度决策算法。该算法使用逐叶策略进行树的生长,并找到具有最大方差增益的叶子进行分割。此外,还可通过计算变化增益的方式将其与其他梯度决策模型加以区分。在LightGBM 中,考虑到弱学习器与强学习器的区别,根据子集估计方差的最大增益对实例进行分割。
2.1 数据处理
若数据出现缺失,则所用算法的表现可能不佳,因此需要对数据加以处理,即数据清洗[12-14]。文中数据处理根据以下规则对所有数据集中的缺失值进行替换:若缺失观测值的数量少于该特征实例总数的5%,则删除这些观测值;而在其余情况下,缺失值将替换为相应特征的众数;此外,还对可能的异常值进行了分析。
数据处理的第二阶段是将分类特征转换为数值,以便于后续处理。
2.2 模型训练
为了对测试集进行预测,LightGBM 训练过程中使用的主要参数为叶子数、叶子中的最小数据量与线程数,目标是通过梯度决策树算法使数据回归。同时采用分层随机抽样方法(Stratified Random Sampling)将已处理过的数据集划分为更小的组[15],且该方法的分层是根据相似的属性或特征形成的。此外,在LightGBM 中有必要为执行的所有训练定义层数。通过使用分层随机抽样方法,可以提供更多的子集来训练模型,进而使模型表现更优。
2.3 评价标准建立
在所有可能的模型评估指标中,均方根误差(RMSE)没有物理单位,其可用于衡量LightGBM 和XGboosting 预测值之间的差异。故该文选用RMSE跟踪预测误差的大小并衡量模型的执行情况[16]。RMSE 是对预测值与实际值的差的平方求均值后的平方根,计算公式为:
式中,n是观察次数,yj是预测值,是实际值。
3 实验验证
首先对梯度提升决策树算法部署进行实验验证,将迭代次数固定为1 000 次,并计算了时间与RMSE 等输出度量,具体如图2 所示,其中RMSE 为虚线上每个点的标签。观察图2 可知,对于较小的学习率,当时间最大时训练精度的表征RMSE 并不是最优的。而随着学习率的增加,处理时间逐渐减少,但RMSE 值的变化并未出现明显差异。因此,在将该算法用于锅炉的最优控制策略时,需要在训练时间成本与准确性之间做取舍。
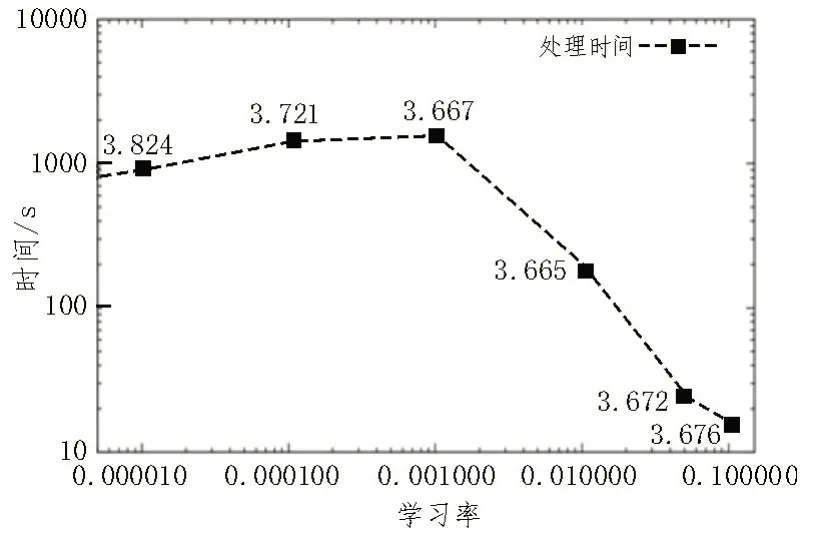
图2 时间、RMSE与学习率的关系曲线
为了对选择部署的模型进行说明,该文对两种梯度提升决策树技术的部署算法LightGBM 和XGBoosting 进行了验证,以证明LightGBM 作为梯度提升决策树组合模型的性能更优。因此,为这两种情况设置了相同的参数集及固定的学习率、迭代次数等信息。测量二者的RMSE,结果如图3 所示。从图中可以发现,LightGBM 在使用的所有学习率间隔中均比XGBoosting 表现更优,由此表明了LightGBM更适用于设计锅炉燃烧的优化控制策略。
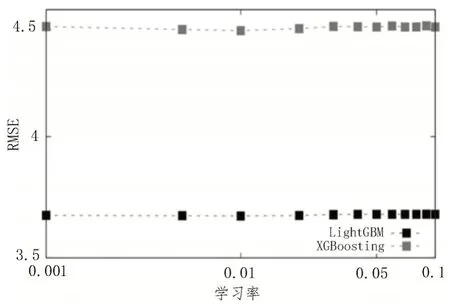
图3 LightGBM和XGBoosting性能对比实验
此外,为了验证文中基于梯度提升决策树的锅炉燃烧最优控制策略的优越性,还设计了两种情形。表1 为两种情形的具体参数,包括各种初始条件。实验1 相比于基本实验情况,入口温度更高,故其出口温度也会较高。这便需要在控制反应物流通量的基础上,对反应炉的压力与温度加以控制,因而也对燃烧控制算法提出了更加严苛的要求。而实验2 所代表的情形中,在提高了压力的基础上降低了入口温度,因此控制算法将重点改变反应物的流通速率。

表1 优化实验参数
优化控制策略增加前后的对比实验如图4 所示。由图可知,实验1 有更长的热回收过程,即出口气体温度保持额外的时间约为300 s;实验2 的输出能量随着过程的发展而逐渐降低。通过积分运算可知,优化前的基本情景能够产生36.6 MW·h 能量,实验1 产生45.9 MW·h 能量,增加了26%的产能;实验2产生了43.2 MW·h 能量,增加了18%的产能。
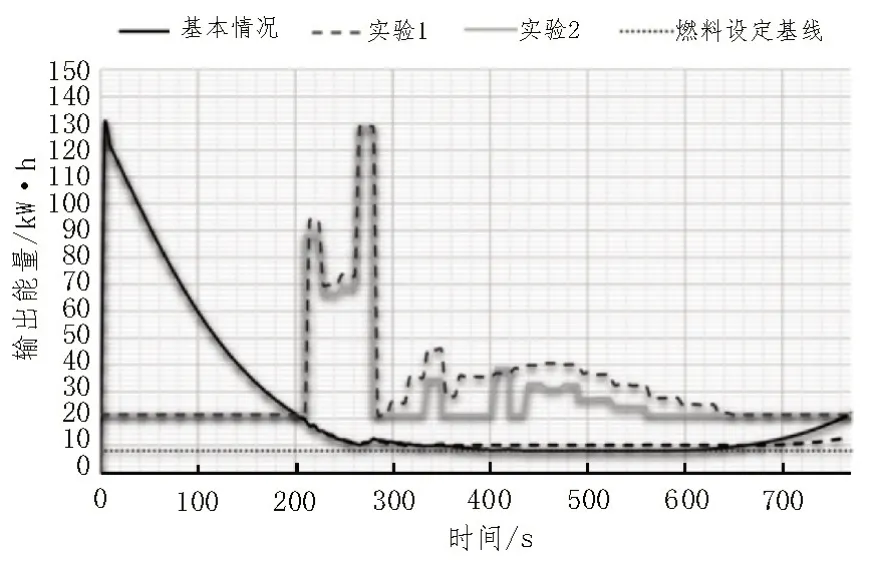
图4 优化控制策略增加前后的对比实验
4 结束语
为了提高燃烧效率,文中对具体燃烧的情况进行了分析,并建立了燃烧粒子的锅炉燃烧模型,实现了对于气态流体在反应炉中时空运动的准确描述,从而为控制策略的设计提供准确的系统模型。但由于燃烧粒子模型数据量较大,传统的单输入输出控制算法难以进行准确控制,因此该文引入梯度提升决策树技术,研究了大量数据情况下锅炉燃烧的最优化控制策略。通过实验,对算法的部署及控制算法的有效性进行了探索。
锅炉模型建模的复杂程度,会进一步决定优化策略的有效性。此外,使用传感器网络进行控制反馈,对于控制精度的提升也具有重要意义。因此,该研究的下一步工作将在有限计算资源的情况下进行,以提高建模的精度,并建立高效、准确的传感器网络,从而实现更为环保的锅炉燃烧控制算法。

