卫河流域河南段不同时期水环境风险评估

张彦，邹磊，窦明，李平，梁志杰

（1.中国农业科学院农田灌溉研究所，河南 新乡453002；2.郑州大学水利与土木工程学院，郑州450001；3.中国科学院地理科学与资源研究所陆地水循环及地表过程院重点实验室，北京100101；4.郑州大学生态与环境学院，郑州450001；5.农业农村部农产品质量安全水环境因子风险评估实验室，河南 新乡453002）

随着社会经济的快速发展和人民生活水平的不断提高，诱发流域水环境问题日益凸显，流域水环境风险不断增加，从而限制了流域水环境绿色健康持续发展[1-2]。流域水环境风险是指河湖水体受到有毒有害污染物的污染风险，进而给河湖水生态环境健康带来危害，其影响因素主要有风险源、河流特性、自然地理和社会发展条件以及水污染治理能力等[3]。目前，利用贝叶斯、蒙特卡罗、神经网络、遥感（RS）和地理信息系统（GIS）等技术方法建立的随机模型、灰色模型、模糊模型、信息熵模型、健康风险评估模型以及生态系统服务功能（INVEST）和德尔菲法风险评估模型等被普遍应用于流域水环境风险评价中[4-6]，如：王泽正等[7]通过贝叶斯网络拓扑结构分析与启发式搜索算法快速辨析了饮马河流域内典型污染来源及其污染贡献；祝慧娜等[8]构建了河流水环境污染风险模糊综合评价模型对湘江水环境风险进行评价；徐凌云等[9]和叶帮玲[10]分别利用INVEST和RS+GIS风险评估模型对黑水河流域和湘江长沙段水质污染发生风险进行了评估；宋策等[11]、王越兴等[12]和李中原等[13]分别利用二维水流水质模型、压力-状态-响应模型和健康风险评估模型对汉江上游水源地、深圳水库水源地以及白龟山水库水源地的水质风险及健康风险进行了评估；Derbalah 等[14]运用风险商方法对日本河流的生态毒理学风险进行了评估；施恩等[15]和罗昊等[16]分别建立了适用于辽河流域辽宁段和流溪河流域水环境累积风险的评估体系；李海燕[17]利用GIS 技术和相对风险评价模型对大宁河水环境风险进行评估并划分了风险等级；Zhu 等[18]、Xu 等[19]和Safakhah 等[20]分别评估了有机物在白洋淀和抚河、黄浦江及伊朗波斯湾北端穆萨河口中的水环境生态风险。

此外，Copula函数作为一种计算变量间风险概率的方法，被广泛应用于降水径流丰枯遭遇、水质水量联合分布和水生态环境稳态关系分析中[21]，如：杨蕊等[5]构建了基于Vine Coupla函数的水环境多因子联合风险模型并识别出了南四湖潜在水环境多因子联合风险；牛军宜等[22]运用Copula函数理论定量地分析了水体污染物的超标风险概率；张彦等[23]和王起峰等[24]基于Copula函数分别评估了小型湖泊和太湖不同分区富营养化的风险。虽然Copula函数理论目前已应用于水环境风险研究中，但其中大部分仅注重单一的水质、水量或污染物的超标风险，而整体上河流水环境组合风险评估的研究相对较少，为此本研究以卫河流域河南段为研究对象，选择卫河流域河南段4个主要的监测站点和3个水体污染物指标，在建立边缘分布、Copula联合分布函数的基础上，定量分析卫河流域河南段不同时期水体污染物指标间的组合风险概率，研究成果对卫河流域水环境管理和综合防治具有一定的指导意义。

1 材料与方法

1.1 研究区概况及数据来源

卫河属于海河流域漳卫南水系，其发源于山西省陵川县夺火镇，至河北馆陶与漳河汇合，流经河南省焦作市、新乡市、鹤壁市、安阳市和濮阳市5 个省辖市，流域面积约为1.53 万km2，流域内主要河流包括卫河干流、大沙河、共产主义渠、淇河、安阳河、马颊河、汤河等[25-26]。卫河流域河南段受到城市扩张以及工农业发展的影响，其水体污染物主要来自于工业废水、生活污水以及农田化肥和农药的施用[27]。根据《2018 年度河南省环境统计年报》，2018 年新乡市、鹤壁市和安阳市废水排放总量分别为31 449.00 万、9 542.93 万t 和16 698.13 万t，化学需氧量（COD）排放总量分别为14 307.04、13 056.43 t和16 607.54 t，氨氮（NH3-N）排放总量分别为1 584.82、1 510.93 t 和3 021.79 t。根据各地市统计年鉴（2021），2020 年新乡市、鹤壁市、安阳市和邯郸市农用化肥施用量分别为51.13 万、6.97 万、40.12 万t 和41.81 万t，农药使用量分别为7 992、892、5 206 t 和5 128 t；辉县市、浚县、汤阴县和大名县农用化肥施用量分别为7.79 万、4.33万、4.06 万t 和4.09 万t，农 药 使 用 量 分 别 为897.4、530、497 t和658.0 t。

本研究数据主要来源于《河南省地表水环境责任目标断面水质周报》、各地市的《地表水环境责任目标断面水质月报》和《环境质量月报》等，本文选取了卫河流域河南段卫河干流的4 个地表水环境责任目标断面的3 项水体污染物指标，监测断面主要有卫辉皇甫、汤阴五陵、浚县王湾和大名龙王庙，具体位置详见图1。水体污染物指标主要为COD、NH3-N 和总磷（TP），监测时段为2015 年7 月至2020 年12 月。在文中所涉及的不同时期中，汛期为6—9 月份，其余月份为非汛期；水质监测数据分析执行《地表水环境质量标准》（GB 3838—2002）。

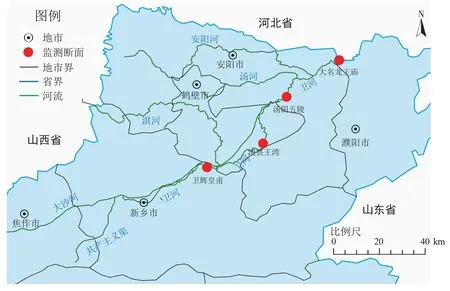
图1 卫河流域河南段水体污染物监测断面分布Figure 1 Distribution of water pollutant monitoring sections at the Wei River basin

1.2 研究方法

1.2.1 边缘分布建立

根据卫河流域河南段4 个监测站点逐月的监测数据，得到水体污染物（COD、NH3-N 和TP）的监测序列{xn|n=1,2,…,N}，N是监测序列的个数。对于监测序列{xn}中的任意一个样本值xm，如果监测序列{xn}中小于xm的数目为Nm，那么可以把xm对应的累积概率表示为：

式中：P（xm）为事件xi≤xm的概率函数；xi为某一水质监测指标。求出监测序列{xn}中所有样本值的概率，得到监测序列{xn}的概率分布曲线。

1.2.2 联合分布概率

假设X、Y和Z分别表示卫河流域河南段水环境事件中具有相互关系的指标序列，其边缘分布函数分别为u=F（x），v=F（y），w=F（z），则其三维联合分布概率的表达式如下[28]：

1.2.3 Copula联合分布函数的建立

卫河流域河南段水体污染是水质恶化的一种综合表征，其评价指标通常由多个水体污染物指标构成，故其水环境组合风险是由水体污染物指标超过标准限值形成不同的组合风险。因此，利用Copula函数建立各水体污染物指标间的联合分布函数，进而定量分析卫河流域河南段的水环境组合风险概率。基于三维Copula 函数的水环境组合风险评估分布模型[28-32] 为：

式中：ρ是对角线上的元素全为1 的三阶对称正定矩阵；Φρ表示相关系数矩阵为ρ的三元标准正态分布的分布函数；Φ-1表示标准正态分布的分布函数的逆函数；tρ，k表示相关系数矩阵为ρ，自由度为k的标准三元t分布的分布函数；tk-1表示自由度为k的三元t分布的分布函数的逆函数。

1.2.4 Copula函数拟合度检验和拟合优度评价

Copula 函数的拟合度检验主要是分析所选用的Copula函数是否合适，能不能恰当地描述变量之间的相关性。通过拟合度检验的Copula 函数可以根据拟合优度评价指标进行下一步的优选Copula模型，本文主要运用K-S 检验的统计量D进行Copula 函数的拟合度检验。拟合优度评价是筛选Copula 函数联合分布概率的重要标准，常用的拟合优度评价方法主要有图形评价分析法、均方根误差法、赤池信息量准则法和贝叶斯信息准则法，这些方法的原理和求解过程可参考文献[28，33] 。

式中：D为K-S 检验的统计量；Ck为联合观测样本xk=（x1k，x2k）的Copula 函数值；mk为联合观测样本中满足x≤xk，同时满足x≤x1k、x≤x2k的联合观测值的个数；n为变量级数的长度；RMSE为均方根误差；MSE为均方误差；AIC为赤池信息量准则；BIC为贝叶斯信息准则；Pc（i）为Copula 函数的多元联合概率分布的计算值；P0（i）为Copula 函数的多元联合概率分布的经验值；m为模型参数的个数。

2 结果与分析

2.1 边缘分布建立

对卫河流域河南段监测断面水体污染物（COD、NH3-N 和TP）的边缘分布函数进行K-S 检验可知，对于监测断面卫辉皇甫，在非汛期和汛期，COD与TP的Pearson 秩相关系数分别为0.430 和0.476（P＜0.01），Kendall 秩相关系数分别为0.224 和0.225（P＜0.05），NH3-N 与TP 的Pearson 秩相关系数分别为0.721 和0.782（P＜0.01），Kendall 秩相关系数分别为0.565 和0.591（P＜0.01）。对于监测断面浚县王湾，在非汛期和汛期，COD与TP 的Pearson 秩相关系数分别为0.637 和0.425（P＜0.01），Kendall 秩相关系数分别为0.427 和0.323（P＜0.01），NH3-N 与TP 的Pearson 秩相关系数分别为0.697和0.576（P＜0.01），Kendall秩相关系数分别为0.513和0.604（P＜0.01）。对于监测断面汤阴五陵，在非汛期和汛期，COD与NH3-N的Pearson秩相关系数分别为0.643和0.631（P＜0.01），Kendall秩相关系数分别为0.425 和0.385（P＜0.01），COD与TP 的Pearson 秩相关系数分别为0.514 和0.678（P＜0.01），Kendall 秩相关系数分别为0.362 和0.448（P＜0.01），NH3-N 与TP 的Pearson 秩相关系数分别为0.560 和0.810（P＜0.01），Kendall 秩相关系数分别为0.499 和0.344（P＜0.01）。对于监测断面大名龙王庙，在非汛期和汛期，COD与TP的Pearson秩相关系数分别为0.531和0.239（P＜0.05），Kendall秩相关系数分别为0.325和0.211（P＜0.05），NH3-N 与TP 的Pearson 秩相关系数分别为0.381和0.741（P＜0.05），Kendall秩相关系数分别为0.338 和0.394（P＜0.05）。受篇幅限制，本文仅将监测断面大名龙王庙不同时期水体污染物边缘分布图列出，如图2所示。由上可知，卫河流域河南段各监测断面水体污染物间均具有较高的相关性，故可以在卫河流域河南段利用Copula 函数建立各监测断面水体污染物间的三维联合分布函数。

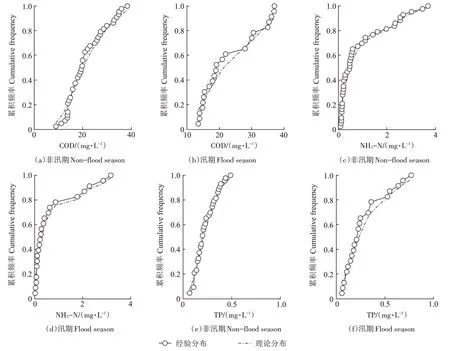
图2 大名龙王庙不同时期水体污染物边缘分布Figure 2 Marginal distribution of the water pollutants at the Daming Longwangmiao station

2.2 Copula函数选择

本文选用Gaussian 和tCopula函数构建卫河流域河南段各监测断面水体污染物（COD、NH3-N 和TP）指标间的三维联合分布模型。三维联合分布模型的参数估计、K-S 检验以及拟合优度评价结果如表1 所示。由表1 可知，各监测断面不同Copula 函数的统计量D在非汛期和汛期均符合K-S 检验的95%显著性水平[D＜0.181（n=43），D＜0.275（n=23），α=0.05] ，表明所选Copula函数均通过检验。

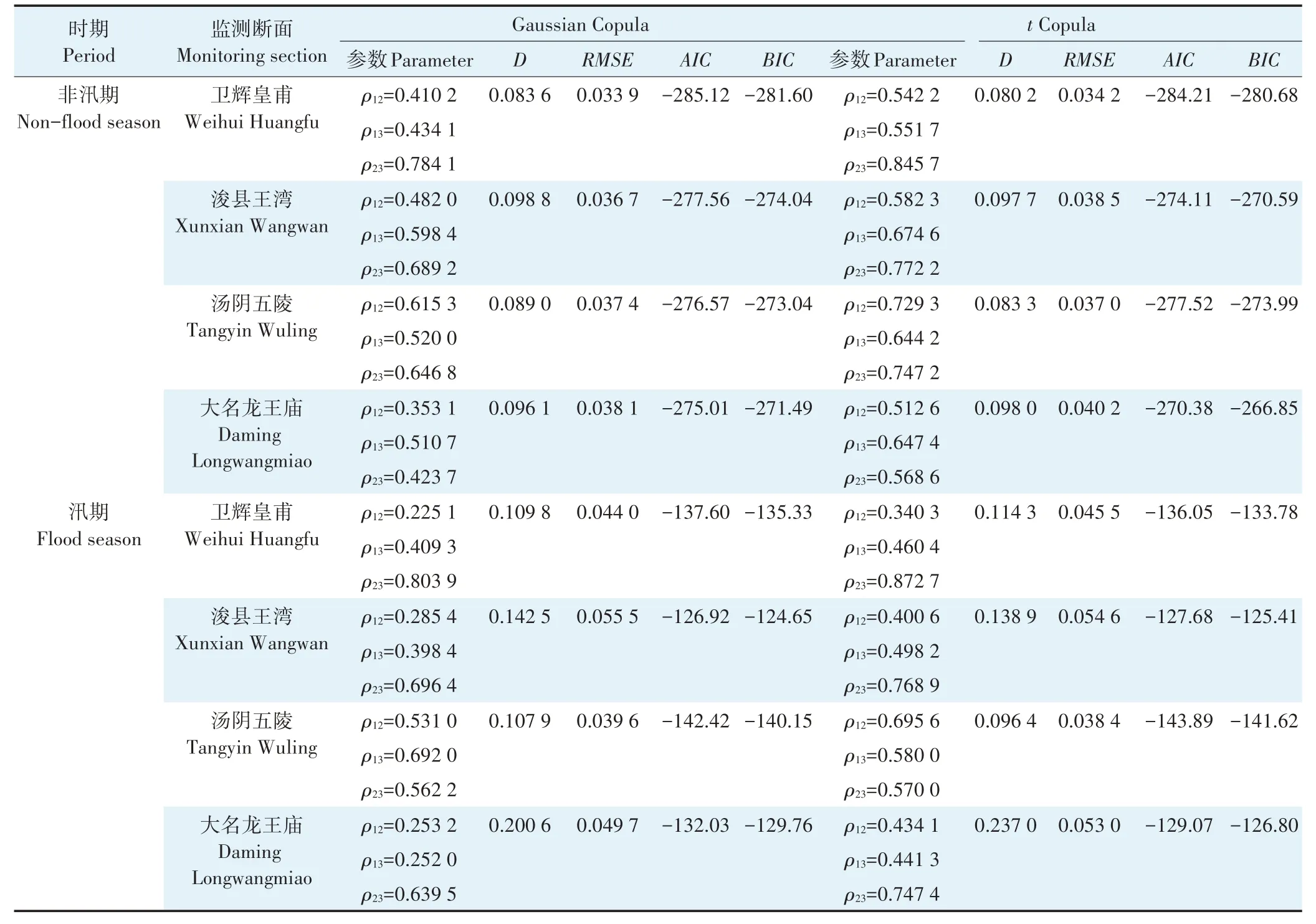
表1 不同时期各监测断面水体污染物指标间的三维联合概率分布拟合优度评价Table 1 Goodness of fit evaluation of the two-dimensional joint probability distribution of the water pollutants at each monitoring section in different periods

利用均方根误差法、赤池信息量准则法及贝叶斯信息准则法对非汛期和汛期各监测断面水体污染物指标间的Copula函数进行拟合优度评价，结果见表1。在非汛期，监测断面卫辉皇甫、浚县王湾和大名龙王庙水体污染物指标间的拟合度最优的均为Gaussian Copula 函 数，其RMSE最 小 分 别 为0.033 9、0.036 7 和0.038 1，AIC最小分别为-285.12、-277.56 和-275.01，BIC最小分别为-281.60、-274.04 和-271.49；监测断面汤阴五陵水体污染物指标间的拟合度最优的为tCopula 函数，其RMSE、AIC和BIC均最小，分别为0.037 0、-277.52 和-273.99。在汛期，监测断面卫辉皇甫和大名龙王庙水体污染物指标间的拟合度最优的均为Gaussian Copula 函数，其RMSE最小分别为0.044 0和0.049 7，AIC最小分别为-137.60和-132.03，BIC最小分别为-135.33 和-129.76；监测断面浚县王湾和汤阴五陵水体污染物指标间的拟合度最优的均为tCopula 函 数，其RMSE最 小 分 别 为0.054 6 和0.038 4，AIC最小分别为-127.68 和-143.89，BIC最小分别为-125.41 和-141.62。因此，分别选择拟合优度最好的Copula 函数构建各监测断面水体污染物指标间三维联合分布模型。

各监测断面水体污染物指标间的三维联合概率函数的理论频率与经验频率的拟合情况如图3 所示。在Gaussian Copula 函数下监测断面卫辉皇甫非汛期和汛期、浚县王湾非汛期、大名龙王庙非汛期和汛期水体污染物理论频率与经验频率间的相关系数分别为0.992 4、0.980 3、0.992 2、0.980 9和0.980 9，在tCopula 函数下监测断面浚县王湾汛期、汤阴五陵非汛期和汛期水体污染物理论频率与经验频率间的相关系数分别为0.986 7、0.992 8 和0.991 1。则各监测断面水体污染物指标间的三维联合概率函数的理论频率与经验频率的拟合情况均较好，表明选取的Copula函数建立的三维联合分布模型较为合理。

图3 不同时期各监测断面水体污染物指标的理论频率与经验频率拟合图Figure 3 Fitting figure of the theoretic and empirical joint frequency between the water pollutants at each monitoring section in different periods

2.3 水体污染物联合风险分析

2.3.1 非汛期水体污染物联合风险概率

基于优选的Copula 函数建立非汛期各监测断面水体污染物指标间的三维联合分布模型，得到水体污染物指标间的联合分布概率P（X≤x，Y≤y，Z≤z）如图4所示，其联合风险概率如表2 所示。由各监测断面水体污染物指标间联合风险结果（表2）可知，在非汛期，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙的水体污染物（COD、NH3-N 和TP）均处于Ⅰ～Ⅲ类水质标准的联合概率分别为14.35%、9.25%、21.61%和26.30%，而均处于劣Ⅴ类水质标准的联合风险概率分别为3.51%、2.14%、2.52%和0.44%。当水体污染物（COD、NH3-N 和TP）中至少有一个指标处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为52.34%、42.04%、42.89%和24.42%。

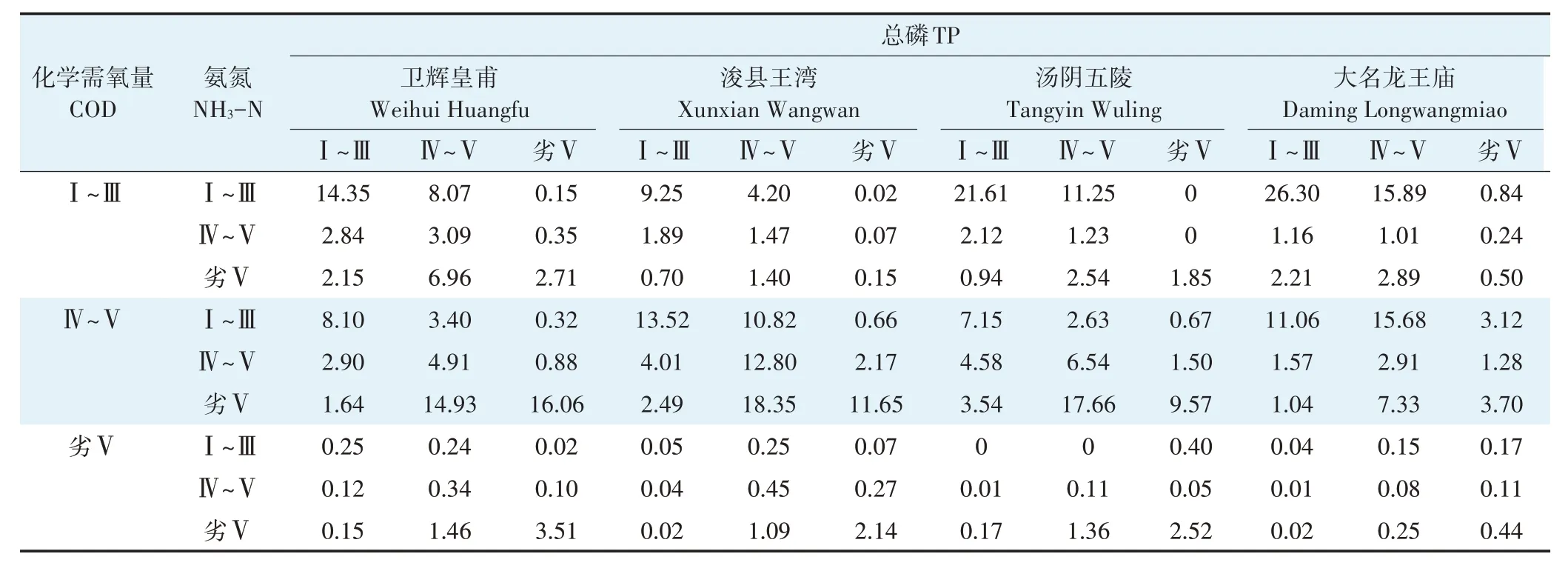
表2 非汛期各监测断面水体污染物间的三维联合风险概率（%）Table 2 Three dimensional joint risk probability between the water pollutants at each station in the non-flood season（%）

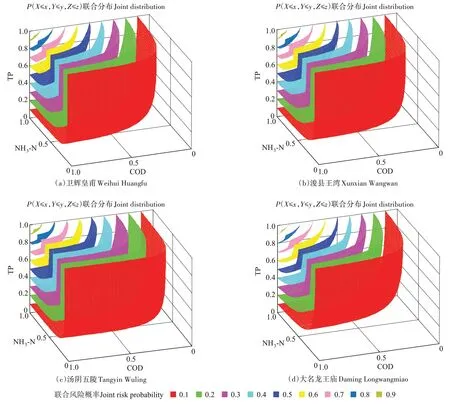
图4 非汛期各监测断面水体污染物指标间的三维联合概率图Figure 4 Joint probability distribution of the three-dimensional Copula functions between the water pollutants at each station in the non-flood season

另外，当仅COD处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为0.95%、0.79%、0.12%和0.28%；当仅NH3-N 处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为25.68%、22.94%、24.68%和13.47%；当仅TP 处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为1.70%、2.92%、2.17%和5.48%。由此可见，当仅NH3-N 处于劣Ⅴ类水质标准时，各监测断面水体污染物的联合风险概率均最大，说明在非汛期卫河流域河南段的主导水体污染物为NH3-N。

2.3.2 汛期水体污染物联合风险概率

基于优选的Copula 函数建立汛期各监测断面水体污染物指标间的三维联合分布模型，得到水体污染物指标间的联合分布概率P（X≤x，Y≤y，Z≤z）如图5 所示，其联合风险概率如表3 所示。由各监测断面水体污染物指标间联合风险结果（表3）可知，在汛期，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙的水体污染物（COD、NH3-N 和TP）均处于Ⅰ～Ⅲ类水质标准的联合概率分别为12.92%、10.45%、12.20%和21.61%，而均处于劣Ⅴ类水质标准的联合风险概率分别为1.45%、1.57%、2.10%和0.59%。当水体污染物（COD、NH3-N 和TP）中至少有一个指标处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为56.53%、29.13%、46.36%和32.42%。

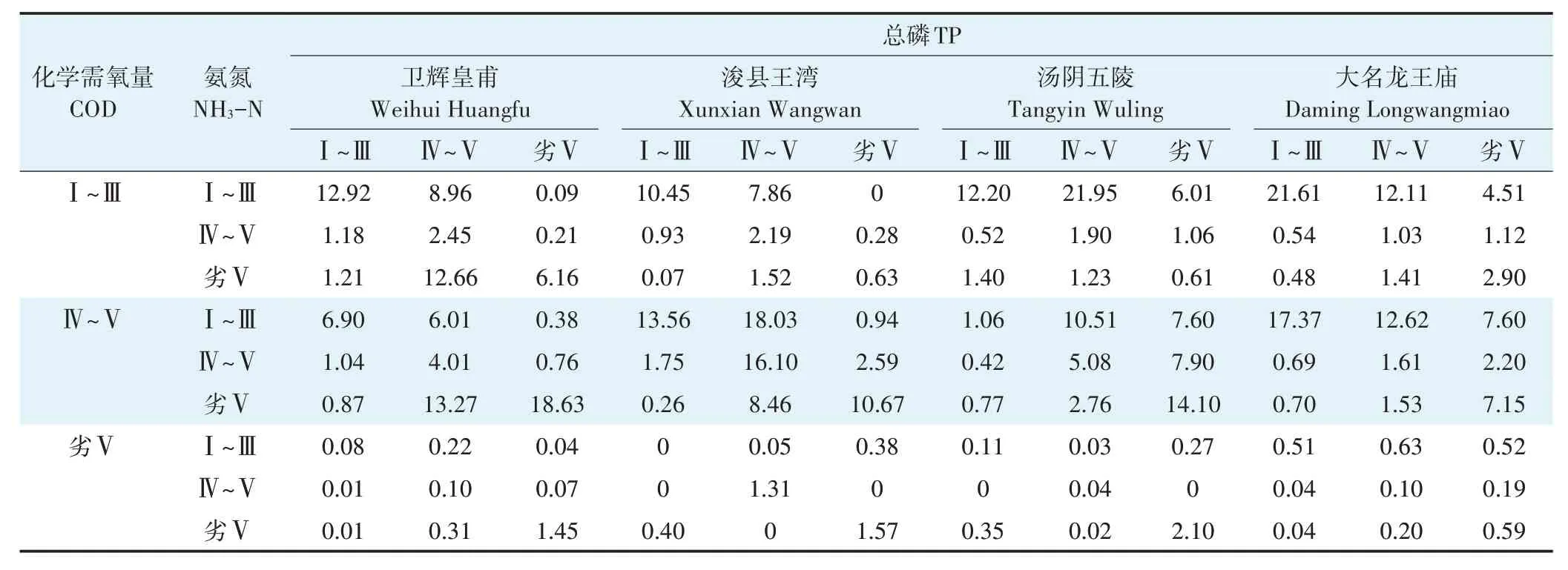
表3 汛期各监测断面水体污染物间的三维联合风险概率（%）Table 3 Three dimensional joint risk probability between the water pollutants at each station in the flood season（%）

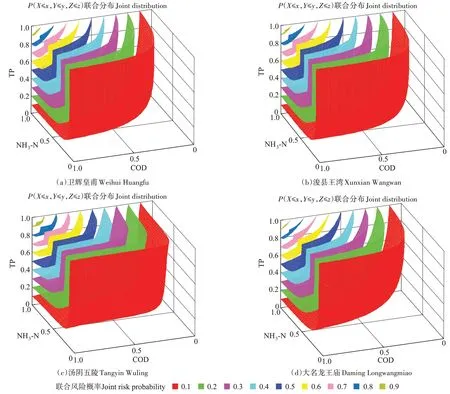
图5 汛期各监测断面水体污染物指标间的三维联合概率图Figure 5 Joint probability distribution of the three-dimensional Copula functions between the water pollutants at each station in the flood season

另外，当仅COD处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为0.41%、1.36%、0.18%和1.28%；当仅NH3-N 处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为28.01%、10.31%、6.16%和4.12%；当仅TP 处于劣Ⅴ类水质标准时，监测断面卫辉皇甫、浚县王湾、汤阴五陵和大名龙王庙水体污染物的联合风险概率分别为1.44%、3.81%、22.57%和15.43%。由此可见，当仅NH3-N 处于劣Ⅴ类水质标准时，监测断面卫辉皇甫和浚县王湾水体污染物的联合风险概率最大，说明在汛期卫河流域河南段监测断面卫辉皇甫和浚县王湾的主导水体污染物为NH3-N；而当仅TP处于劣Ⅴ类水质标准时，监测断面汤阴五陵和大名龙王庙水体污染物的联合风险概率最大，说明在汛期卫河流域河南段监测断面汤阴五陵和大名龙王庙的主导水体污染物为TP。

总体看来，卫河流域河南段监测断面大名龙王庙的水质状况最好，浚县王湾和汤阴五陵的水质状况次之，卫辉皇甫的水质状况最差。

3 讨论

目前，流域水环境面临着污染事件频发、水生态环境破坏等问题，这严重制约了流域经济社会的发展和生态环境保护的进程[34]。根据2021 年新乡市、鹤壁市和安阳市环境质量概要或地表水水质月报，新乡市、鹤壁市和安阳市地表水责任目标断面累计达标率分别为60.5%、88.1%和64.0%，其中卫河流域责任目标断面卫辉皇甫、汤阴五陵和浚县王湾的累计达标率分别为50.0%、75.0%和91.7%，可知卫河流域河南段地表水水体环境仍需进一步改善。卫河流域主要受工业废水、生活污水、畜禽养殖废水以及农业面源污染的影响，因此要从治理城镇生活污染、深化工业污染防治、开展畜禽养殖污染治理、优化生态水量调配、整治城市黑臭水体、减少农村农业面源污染、预防水污染事件等方面组织展开工作，进而改善卫河流域地表水环境质量。

流域水环境风险受到多方面因素的影响，开展流域水环境风险评估可以进一步识别流域水环境风险的主要污染源，进而有针对性地建立流域水环境风险防控系统以降低水环境污染带来的损害。在卫河流域，河南省相关管理部门要求限制废污水的排放，加强农用化肥和农药的控制并防控流域内农业面源污染[27]。本研究表明，与非汛期相比汛期各监测断面水体污染物处于劣Ⅴ类水质标准的联合风险概率略有降低，说明在汛期卫河流域河南段水体环境质量相对有所好转，这主要是因为在汛期河流径流量比较大，对水体污染物的稀释效应增强，同时汛期河流水体的自净能力有所提升。当仅COD处于劣Ⅴ类水质标准时，各监测断面水体污染物的联合风险概率均较小，说明卫河流域河南段主要污染物为NH3-N 和TP，这与李婧等[26]的研究结果一致，即NH3-N 和TP 是河南省辖海河流域的主要污染因子。张亚丽等[35]的研究表明卫河汤阴五陵河段COD基本处于无警和轻警级别，而NH3-N 浓度严重超标且大多是巨警，这与本研究中NH3-N处于劣V类水质标准时，监测断面汤阴五陵水体污染物的联合风险概率在非汛期最大的结果一致。在非汛期时，卫河流域河南段的主导水体污染物为NH3-N，这主要是由于NH3-N 污染主要来自于工业废水和生活污水，且在非汛期时流域河道内径流量较小使得NH3-N 污染程度较大；在汛期时，卫河流域河南段监测断面卫辉皇甫和浚县王湾的主导水体污染物为NH3-N，而监测断面汤阴五陵和大名龙王庙的主导水体污染物为TP，这主要是由于TP 污染主要来自农业面源污染，在汛期时农业面源污染排放的磷使河流水体磷的污染程度增大，这与相关研究表明农业面源排放的磷为地表水污染总负荷的24%～71%是一致的[36]。另外，监测断面汤阴五陵和大名龙王庙分别位于安阳市和邯郸市，其在安阳河和汤河汇入到卫河之后的河段，受到面源污染的范围较大，因此面源污染占据了主导地位，使其主导水体污染物由非汛期的NH3-N 转变为了汛期的TP。总体来说，虽然流域环境质量得到了持续改善，但流域水环境风险及管控形势仍相对严峻，因此要加强流域水环境基准、数据监测以及风险评估等方面的科学研究，提出流域水环境风险管理的战略思路，进一步加强流域水环境风险防控体系建设，为流域水环境综合管理和污染防治提出建议和措施。

4 结论

（1）通过对各监测断面水体污染物联合概率Copula 函数优选，结果表明监测断面卫辉皇甫非汛期和汛期、浚县王湾非汛期、大名龙王庙非汛期和汛期的水体污染物间拟合优度最好的三维Copula 函数为Gaussian Copula 函数，监测断面浚县王湾汛期及汤阴五陵非汛期和汛期的水体污染物间拟合优度最好的三维Copula函数为tCopula函数。

（2）非汛期和汛期各监测断面水质状况具有一致性：大名龙王庙的水质状况最好，在非汛期和汛期其水体污染物均处于Ⅰ～Ⅲ类水质标准的联合概率最大，分别为26.30%和21.61%；卫辉皇甫水质状况最差，在非汛期和汛期其水体污染物有一个指标处于劣Ⅴ类水质标准时的联合风险概率最大，分别为52.34%和56.53%。

（3）监测断面卫辉皇甫和浚县王湾在非汛期和汛期的主导水体污染物均为NH3-N，说明其主要受工业废水和生活污水污染的影响；监测断面汤阴五陵和大名龙王庙的主导水体污染物由非汛期的NH3-N转变为汛期的TP，表明汛期时面源污染占据了主导地位。