长跨度大直径孔系同轴度误差测量方法
程 旭,刘洪霞,郝志华,陈艳红
(1.空军装备部驻沈阳地区第一军事代表室,沈阳 110850;2.沈阳飞机工业(集团)有限公司计量中心,沈阳 110850)
在航空制造领域,诸如飞机的机翼连接件、飞机副翼上的双耳孔、发动机机匣轴承座孔等均属于长跨度孔系零件,这类零件的孔系同轴度制约着飞机装配精度及装配效率,并对飞机运行可靠性和安全性至关重要[1-2]。研究发现飞机的大量机械振动事故是由零部件同轴度不合格所引起的,尤其是长跨度大直径孔系零件。
对于长跨度大直径孔系同轴度误差的测量,目前主要采用长轴塞规测量法、试装法等,不仅效率低,而且难以保证测量精度。三坐标测量机[3]、测量臂[4]等仪器设备又受到被测件体积和结构上的限制,无法满足现场测量需求。
1 测量原理
如图1 所示,大直径孔系同轴度测量系统主要由激光准直模块、激光测距模块和多功能测头组成。激光准直模块利用单模光纤激光器发出的准直激光束作为同轴度测量基准,激光器安装在四自由度工作台上,通过工作台调整激光束的位置和方向。多功能测头的一端是气动夹爪,测量时气动夹爪张开使测头在孔系内获得稳定支撑。测头的另一端装有小型电机、位置敏感探测器(PSD,Position Sensitive detector)、激光测距传感器、双轴倾角传感器及测量电路等。
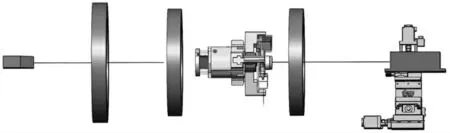
图1 测量系统硬件平台总体结构
通过安装夹具使PSD 传感器光敏面与测头上的激光测距传感器所发射的激光束共面,小型电机旋转轴线与PSD 光敏面垂直。在此基础上建立如图2 所示的PSD 坐标系oxy、测头坐标系OXYZ 和世界坐标系O′X′Y′Z′。其中,PSD 坐标系是PSD 传感器固有的,其原点位于PSD 中心。测头坐标系以电机旋转轴线与PSD 光敏面的交点为原点,其OX、OY 轴分别与PSD坐标系的ox、oy 轴平行。世界坐标系以准直激光器的出射点为原点,以准直光束作为O′Z′轴,O′X′轴处于水平方向,再利用右手法则确定O′Y′轴。
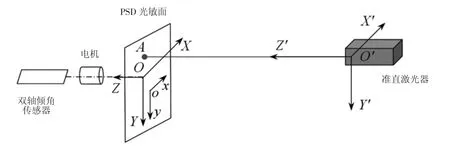
图2 测量系统的坐标系示意图
2 同轴度误差测量
如文献[5-6]所述,无基准孔系同轴度误差评定问题可归为对孔系轴线的直线度误差进行评定。即利用测得的各个孔截面中心点拟合得到一条公共轴线,然后取所有截面中心到该公共轴线距离中最大值的2 倍作为孔系同轴度误差值。
2.1 准直激光光斑位置测量
在测量孔系同轴度的过程中,当多功能测头在孔内稳定支撑后,测头前端的PSD 感知到准直激光束投射在光敏面上的光斑[7-9],并通过下面的式(1)计算光斑中心的坐标[10],进而确定多功能测头在各个测量截面上的相对位置。
式中:Ix1、Ix2、Iy1、Iy2分别为准直激光投射在PSD 上产生的ox 和oy 两个方向的光电流,Sx、Sy分别为这2 个方向上的PSD 光敏面长度。
为减小各种误差因素的影响,选用了温度特性稳定、发散角小的单模光纤激光器为激光源,并在光路中添加滤光片以降低环境光的影响,还设计了滤波电路来降低测量电路中的噪声干扰。图3 给出了在距离激光器1 000 mm 处PSD 传感器采集到的10 min 的光斑坐标数据。

图3 PSD 传感器采集的激光光斑中心坐标
从图3 中可以看出,尽管采取了上述一系列措施,但2 个方向上的光斑中心坐标仍存在10 μm 左右的波动,从而导致在测量孔截面中心坐标时出现较大误差。因此,本文结合卡尔曼滤波[11-12]与均值滤波[13-14]算法,对PSD 采集的数据进一步进行软件滤波。如图4 所示,通过该滤波算法,2 个方向上的激光光斑中心坐标波动均减小到2 μm 左右。
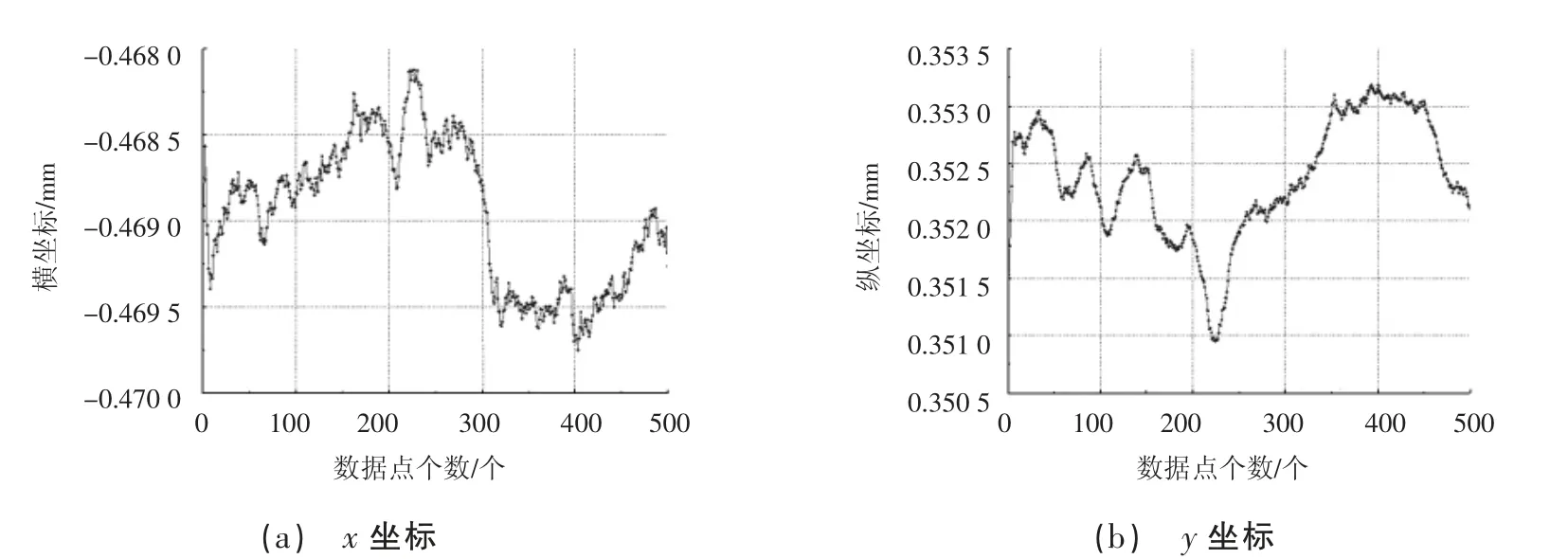
图4 滤波后的激光光斑中心坐标
2.2 坐标系转换
根据图2 所示的各坐标系之间的关系,测头坐标系中的点(X,Y,Z)在世界坐标系中的坐标(X′,Y′,Z′)满足
式中:2 个坐标系之间的转换矩阵H 可由下面的式(3)表示。
式中:α、β、γ 分别为测头坐标系绕世界坐标系的O′X′、O′Y′和O′Z′轴旋转的角度,(tX,tY,tZ)为测头坐标系原点在世界坐标系下的坐标。由于α、β 在实际应用中很小,取α=β=0。γ 为多功能测头的滚动角,即双轴倾角传感器的读数。当γ=0 时,多功能测头处于水平姿态。
假设在被测孔系内测量了m 个截面,则在任意截面i(i=1,2,…,m)上,电机带动PSD 和激光测距传感器旋转一周,PSD 采集到n 个光斑中心坐标(xj,yj),j=1,2,…,n。同时,激光测距传感器和电机角度编码器分别测得对应的孔截面轮廓点距离dj和电机旋转角度值θj。
根据光斑中心轨迹(xj,yj)可以拟合得到PSD 的旋转中心(xO,yO),该点为电机旋转轴线与PSD 光敏面的交点,即测头坐标系的原点O。旋转PSD 传感器使其ox 轴处于水平方向,此时PSD 测得的激光光斑坐标为A(xA,yA),点A 为世界坐标系的O′Z′轴与PSD 光敏面的交点。由于测头坐标系的OX 和OY 轴分别与PSD坐标系的ox、oy 轴平行,因此点A 在测头坐标系下的坐标为(xA-xO,yA-yO),式(3)中的tX=-(xA-xO),tY=-(yAyO)。由图2 可知,tZ的值等于O′A 的距离,由激光测距模块测量得到。
按照上述方法确定了转换矩阵H 以后,再利用多功能测头在测量截面上获取的距离值dj和电机旋转角度值θi,通过圆拟合算法得到截面中心在测头坐标系下的坐标为B(XB,YB,ZB)。点B 在世界坐标系下的坐标(X′B,Y′B,Z′B)可由下面的式(4)计算得到。
2.3 公共轴线拟合
移动多功能测头在孔系内测量多个截面后,根据各截面中心点采用最小二乘法拟合公共轴线。假设该公共轴线经过世界坐标系中的一点Q0(X′0,Y′0,0),方向向量为(p,q,1),则该轴线的参数方程可表示为
式(5)中的X′0、Y′0、p、q 分别由下面的式(6)计算得到。
式中:n 为测量截面的个数,(X′i,Y′i,Z′i)为第i 个截面中心的世界坐标。
3 实验分析
3.1 孔截面中心坐标测量
按照2.2 节的方法计算出孔截面中心的坐标,图5给出了10 次重复测量的结果。从图5 中可以看出,测得的各个截面中心处于直径11 μm 左右的区域范围内,达到了良好的测量重复性。
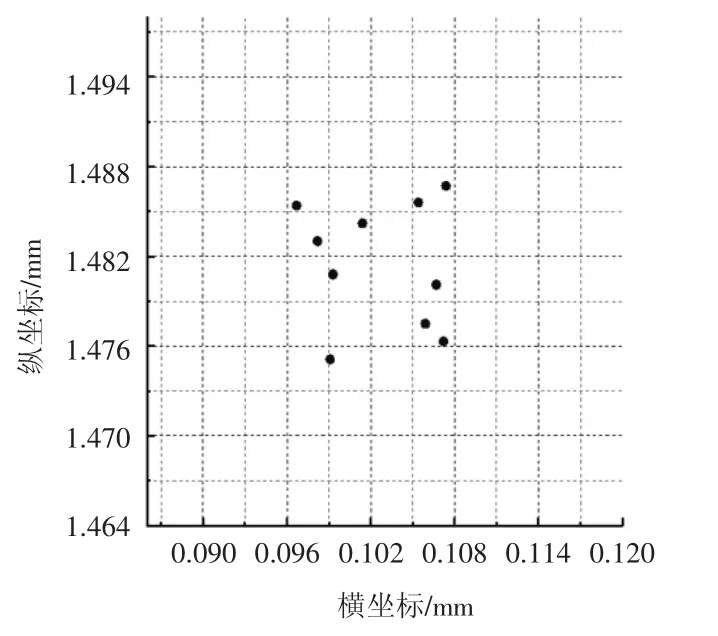
图5 孔截面中心坐标的重复测量结果
3.2 孔系同轴度测量
测量孔系的同轴度,每个孔零件测量4 个截面,重复测量10 次,计算出孔系同轴度测量结果的重复性误差为0.004 2 mm。
3.3 实验误差分析
长跨度大直径孔系测量系统的测量误差主要来源于测头机构的装配误差和传感器本身的测量误差。本文采用蒙特卡洛法对系统的测量不确定度进行评定[15],使用Matlab 进行仿真计算,实验次数为105次,得到的概率密度分布直方图和累积分布曲线分别如图6(a)和(b)所示。结果显示,本系统测得的孔系同轴度误差平均值为0.384 5 mm,标准不确定度为0.004 5 mm,包含概率为95%的置信区间为[0.376 1,0.394 1]。
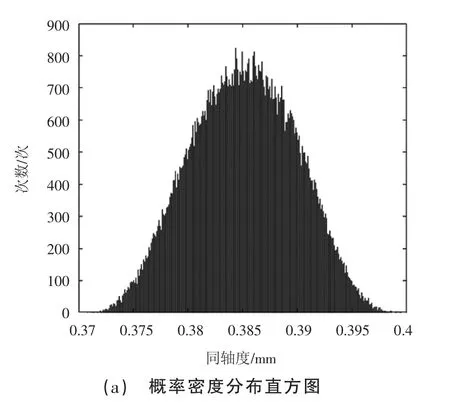
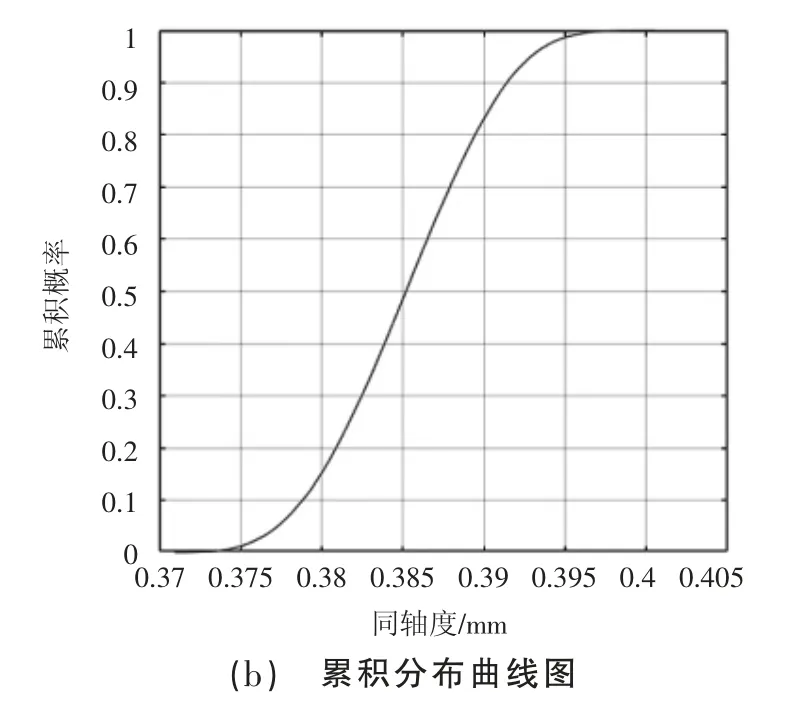
图6 基于蒙特卡洛法的孔系同轴度误差测量不确定度分析结果
4 结论
提出了一种基于光电检测的大直径孔系同轴度误差测量方法,开发了相应的测量装置并进行了实验验证。系统测量不确定度优于0.004 5 mm,能够满足轴承座孔等长跨度大直径孔系的同轴度误差测量要求。采用准直特性好的单模光纤激光器作为准直光源,并将卡尔曼滤波与均值滤波相融合构建滤波算法,减小了准直激光光斑位置测量的随机误差,增强了PSD 传感器的抗干扰能力,提高了测量系统的鲁棒性。

