基于K-means聚类的奥林匹克获奖研究分析

吴会会 袁哲 惠小健 章培军 卢鸿艳

摘  要：奥林匹克运动会是由国际奥林匹克委员会主办的每隔4年举行的一届国际性的运动会，各个国家获得的奖牌总数也直接反映了该国的体育建设水平与人民的精神文明程度。文章根据国家统计局、联合国相关机构、国际奥委会公布的数据，以参赛员的性别、年龄、身高、体重作为因变量，是否获奖作为自变量建立决策树和K-means聚类，对是否获得奖牌进行预测，并对其进行分析。

关键词：奥林匹克；K-means聚类；预测

中图分类号：TP399  文献标识码：A  文章编号：2096-4706（2023）15-0136-05

Analysis of Olympic Award Based on K-means Clustering

WU Huihui， YUAN Zhe， XI XiaoJian， ZHANG Peijun， LU Hongyan

（School of Computer Science， Xijing University， Xi'an  710123， China）

Abstract： The Olympic Games is an international games held every four years sponsored by the International Olympic Committee， and the total number of medals won by each country also directly reflects the country's level of sports construction and the spiritual civilization of the people. Based on the data released by the National Bureau of Statistics， relevant agencies of the United Nations and the International Olympic Committee， this paper establishes a decision tree and K-means clustering based on the gender， age， height and weight of the participants as the dependent variables， and whether or not to win the medal as the independent variable， and forecasts whether to win the medal and analyzes it.

Keywords： Olympics; K-means clustering; forecast

0  引  言

奧林匹克运动会主要是以体育运动为主的每四年为一个周期的运动会，它的顺利如期的开展促进了人的全面发展，涵盖了生理、心理以及社会道德等各个方面，为各国之间的往来沟通搭建起了一个桥梁，在全世界的见证下，为世界的和平稳定发展加固了堡垒。奥林匹克运动不仅仅是现代社会中体育文化的一种体现，还以一种独特的魅力愉悦身心，更蕴含着一种生生不息的人文精神，催人奋进。奥林匹克运动是工业革命时期的一种产物，加强了世界各族人民的联系，不局限于经济、政治、文化，还跨越了地域之间的差异，是人类社会进展到一按时期的必然产物。

机器学习算法可分为监督学习[1]和无监督学习[2]。监督学习常用于分类和预测。是让计算机去学习已经创建好的分类模型，使分类（预测）结果更好的接近所给目标值，从而对未来数据进行更好的分类和预测[3]。因此，数据集中的所有变量被分为特征和目标，对应模型的输入和输出；可将其分为训练数据集和测试数据集，分别用于训练模型的参数以及此对此模型的测试与评估。常见的监督学习算法有Regression（回归）、KNN和SVM（分类）。无监督学习常用于聚类。输入数据没有标记，也没有确定的结果，而是通过样本间的相似性对数据集进行聚类，使类内差距最小化，类间差距最大化。无监督学习主要是通过对数据集的分析主动去学习如何做事情，而不是让计算机去怎么做。常用的无监督学习算法有K-means、PCA（Principle Component Analysis）。

聚类算法[4]又叫做“无监督分类”，其目的是将数据划分成有意义或有用的组（或簇）。这种划分可以基于业务需求或建模需求来完成，也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中，如果手头有很多的客户信息，那么就可通过聚类的方式将这些客户信息进行分类，以便顺利的开展接下来的工作。再比如，聚类可以用于降维和矢量量化，可以将高维特征压缩到一列当中，常常用于图像、声音和视频等非结构化数据，可以大幅度压缩数据量。本文研究的是无监督学习里的K-means算法[5]，主要以历年来参赛员的性别、年龄、身高、体重等各种指标为研究对象，预测获得奖牌情况，为后续运动员的培养提供一些建议。

1  K-means算法

目前使用最广泛的聚类算法就是K-means算法，K-means算法也成为K-均值或K-平均。该算法首先随机地选择K个对象作为初始的K个簇[6]的质心；然后对剩余的每个对象，根据其与各个质心的距离，将它赋给最近的簇，然后再对每个簇里的质心进行重新计算，依次循环下去，直到目标函数收敛，目标函数一般为平方和误差，即SSE（sum of the squared error），可用如下公式来进行表示：

上述公式表示的是对所有的研究对象的平均误差进行求和，其中参数p表示所要研究的数据对象，mi表示是簇Ci的一个平均值。K-means算法的优点是：聚类速度快，聚类的效果好，鲁棒性好，所以本文选择了此算法对历年来的各国获奖情况进行了一个分析。

2  决策树

决策树[7]是通过一定规则对数据进行分类的一树状结构，它从根节点开始，测试原始的样本数据集，根据测试的结果可将其分成不同种类的子集，这些子集就构成了一系列的子节点。决策树大致可以分为回归树与分类树两大类，其中回归树主要是对连续的数据集进行分类的一种决策树，而分类树主要是对离散数据集进行分类的一种决策树。

决策树是一种树状的结构，其每个根节点可以看作是全部的数据集，分节点可以看作是测试每个变量，其可将数据集分成很多个子集；叶节点可以看作是对数据集类别的一种记录方式，那么决策树的整个运行过程可以简述为以下几步：1）将整个数据集看作是决策树的一个训练集，通过每个数据的属性将其分好类，依据一定的标准将类别进行量化，以达到一个最好的分类结果。2）重复第一个步骤，直到每个叶节点都归属到同一个类别，依次循环下去，穷尽所有节点，直至充满整个树。通过决策树可以准确地找到数据属性与类别之间所蕴含的关系，进而可将其用来预测一些未知的未做记录的数据集。其产生的过程实质上就是对研究的样本不断地进行分组，核心就是属性的选择问题。

决策树的应用非常广泛，其具有如下的一些优点：1）决策树算法很容易实现，理论基礎简单，在学习的过程当中不需要去了解数据的背景，即可体现出数据本身所具有的结构特点，鲁棒性比较好。2）可对大量的数据进行分类，并且运行时间短，效率高，能够同时处理数据的类型以及数据属性。

3）可通过静态的测试方式对模型进行一定的测试，可以测试出实验过程中模型的可信度，为实验的可行性提供了一些理论依据。鉴于以上的优点，本文利用了决策树这个算法，以参赛员的性别、年龄、身高、体重作为因变量，是否获奖作为自变量建立了决策树，对是否获得奖牌进行了预测分析。

3  数据分析

3.1  数据集

本文的数据是选自国家统计局、联合国相关机构、国际奥委会公布的数据。里面有现代奥运会的历史数据集，包括所有从1896年雅典到2016年里约热内卢的数据，其中冬季和夏季运动会在同一年举行，直到1992年。之后，冬季运动会以四年为周期进行开展，从1994年开始，然后是1996年的夏季，然后是1998年的冬季，依此类推。

3.2  数据清洗

为了减少预测结果的误差，需要对原始数据集进行预处理，通过查看数据集，发现数据集中Age、Height、Weight、Medal列存在部分的缺失值。其中Medal的缺失值表示的是运动员在此比赛项目上是否得到过奖牌，将所缺失的值用0代替，其表示的含义是没有获奖。所以除了Medal那列，将其余的所有空值的行进行删除，再对数据进行分析。

3.3  数据可视化

本文对男女参加奥运会的人数进行了分析，如图1所示。

从图1可以看出，女性参加运动会的人数要比男性参加的人数少得多，但是从整体上看，女性参加冬季奥运会要多一些，男性参加夏季奥运会要多一些，这个总体差异不是特别大。

本文对每届参加奥运会的运动员人数进行了分析，如图2所示。

由图2可得，1896年开始到1980年夏运会参赛运动员数量呈现一个曲折上升的趋势，这是因为此时处于世界格局动荡期，战争、国家间冷战摩擦等事件很大程度影响了奥运会举办的客观条件，与此同时冬运会也类似，但由于参赛项目少和知名度低等原因参赛人员本身就大大低于夏奥会，所以趋势不是很明显；图表显示到了1980年，世界64个国家联名抵制苏联奥运会使参赛人数出现最大一次下降幅度，此后世界形势渐渐明朗，经济贸易和外交逐渐恢复，奥运会也进入了同步的快速增长和稳定阶段。

本文对每届奥运会的比赛项目进行了分析，如图3所示。

图3是关于奥运会比赛项目的变化折线图，可以看出在1980—2000年这20年，比赛项目增长趋势最大，且以夏季奥运会尤为突出，但最近十几年比赛项目增加趋势慢慢变为平稳的态势了。

本文对每届参加奥运会的国家进行了分析，如图4所示。

图4是关于参加奥运会国家数量的变化趋势的，其中有两届奥运会存在变化的。1976年蒙特利尔奥运会：由于25个国家，其中大部分是非洲人，抵制奥运会，抵制南非的种族隔离政策。1980年的夏季奥运会上，非洲国家在夏季奥运会上的出席人数有限，因此参加了1980年的冬季奥运会。奥运会史上的种族歧视事件。1980年莫斯科奥运会：为了应对苏联入侵阿富汗，包括美国在内的66个国家抵制参加奥运会。政治事件对奥运会的影响也是颇深的。

本文对每届奥运会各个国家获得奖牌的数量进行了分析，如图5所示。

图5选取了获得奖牌数目大于300的国家，通过比较发现美国不管是金牌、银牌还是铜牌都领先很多，从金牌榜来看，占据头把交椅的是美国，金牌数量接近2 500枚，是苏联的三倍之多，可谓是一骑绝尘。我国的奥运事业由于种种原因起步比较晚，直到1986年才正式派出队伍参加奥运会，目前的累计金牌数量为334枚，排名在第11位。

本文对每届奥运会的运动员的年龄以及所获得的奖牌进行了分析，如图6所示。

从图6可以看出，运动员参加奥运会的年龄主要集中在15～40岁之间，而获得奖牌的几率与年龄分布大致相同，其中24岁和25岁获得的金牌数量是最多的。由此可以看出年轻人获得金牌的几率要大很多。

本文对每届奥运会的运动员的身高和体重进行了分析，如图7所示。

从图7中可看出：运动员的体重均在75 kg左右，身高均在180 cm左右获得奖牌的可能性是最大的。

4  奥林匹克获奖的研究分析

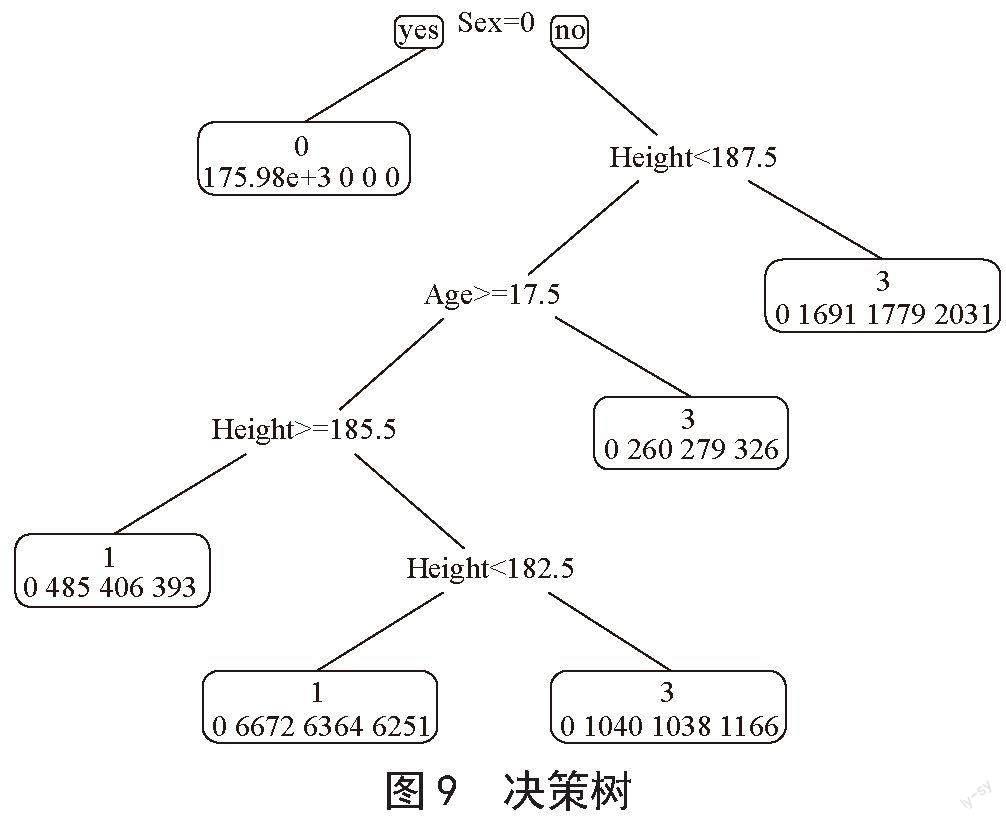
选取运动员的性别，年龄，身高，体重作为因变量，获奖作为自变量，在建立获奖影响因素模型之前，首先进行数据分割，即将数据分割为训练集和测试集，将数据的70%划分为训练集，30%划分为测试集。训练集用于训练模型，测试集用于测试模型效果。建立决策树，得到特征重要性如图8所示。

从图8可以看出体重对获奖情况的影响比较大，身高次之，性别影响最小。由此所建立的决策树如图9所示。

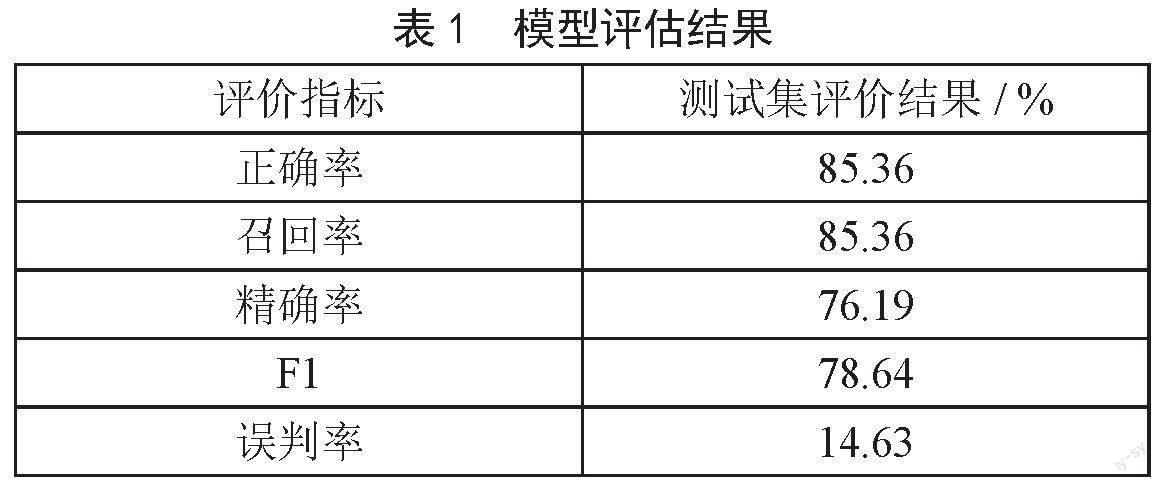
用所建立的决策树分类预测模型，预测模型对测试集数据进行拟合优度测试，生成判断结果，如表1所示。

由表1可以看出，决策树分类预测模型的判断正确率为85.36%，达到比较理想的整体预测效果。

然后再选举运动员的性别，年龄，身高，体重进行K-means分类，分成3类，如图10所示。

以获奖情况为训练集的混淆矩阵，如表2所示。

由表2可以看出，K-means分类预测模型的判断正确率为83.80%，达到较理想的整体预测效果。

由实验结果可以得出，随着时间推移，奥运会赛事数量整体呈现上升的趋势，且夏季奥运会赛事数量明显远超与冬季奥运会赛事数量；1896年开始到1980年夏运会参赛运动员数量呈现曲折上升的趋势，这是因为此时处于世界格局动荡期，战争、国家间冷战摩擦等事件很大程度影响了奥运会举办的客观条件，同理冬运会也类似；男性夏运会参赛运动员人数是和历年运动员数量变化同调的，女性夏运会参赛运动员人数明显的持续增长，并在1980年到2000年间持续大幅上涨。120年来的奖牌数量排名如下，USA为最多，CHN（中国）为第17名。由以上的分析可以得出，奥林匹克运动的获奖情况和运动员自身的性别，年龄，身高，体重是紧密联系的，其中影响最大的是体重。因此在下一阶段可考虑控制一下运动员的体重。

5  结  论

近几年，奥运会赛事数量以及参赛运动员的数量整体呈现上升的趋势，中国队从1984年开始获得过奖牌，随后奖牌总数逐年上升，在2008年主场举办的奥运会上奖牌数达到最高，其中常夺金牌的项目有女子排球、男子体操、男子单雙人乒乓球等。通过分析可以发现，奥林匹克运动的获奖情况和运动员自身的性别，年龄，身高，体重是紧密联系的，其中影响最大的是体重。因此在下一阶段可考虑控制一下运动员的体重。

参考文献：

[1] 吕高锋，谭靖，乔冠杰，等.决策树报文分类算法 [J].国防科技大学学报，2022，44（3）：184-193.

[2] 于莉佳，汪涛.基于模糊K均值聚类的高校网络用户行为分析 [J].智能计算机与应用，2022，12（10）：200-202.

[3] 熊斗寅.开展奥林匹克教育必须持之以恒 [J].体育学刊，2020，27（2）：8-10.

[4] 刘洋，王慧琴，张小红.结合蚁群算法的改进粗糙K均值聚类算法 [J].数据采集与处理，2019，34（2）：341-348.

[5] 王惠琴，侯文斌，彭清斌，等.基于K均值聚类的SPPM分步分类检测算法 [J].通信学报，2022，43（1）：161-171.

[6] 潘丹，李永周，王晓洁.高校科技创新能力比较研究——基于组合评价法和K均值聚类的分析 [J].中国高校科技，2020（5）：30-34.

[7] 周平，马景义.基于路径跟随方法的光滑子区间K均值聚类算法 [J].统计与决策，2022，38（12）：17-22.