一种动态加权条件网络数据的特征标记算法

温志峰

摘  要：针对传统特征标记方法在面对海量的网络数据时出现的定位目标信息困难、时间和空间开销较大等问题，提出基于加权遗传算法的互信息特征反馈标记方法。首先优化数据处理流程，对目标数据特征进行加权处理，得到近似全局最优解；其次用户对文本特征或者图像实例完成标记，基于用户的标记与未标记情况构建双重监督图；最后建立实数值推测函数并计算，获取双重监督图中未标记的结点。通过仿真实验结果，验证了方法误差较小、检索精度较高，能够实现在大量的数据中快速找到目标内容。

关键词：加权遗传算法；互信息；双重监督图；实数值函数；近似全局最优解

中图分类号：TP391.1；TP391.9 文献标识码：A 文章编号：2096-4706（2023）15-0087-04

Feature Marking Algorithm Based on Dynamic Weighted Conditional Network Data

WEN Zhifeng

（College of Information Engineering， Guangdong Innovative Technical College， Dongguan  523960， China）

Abstract： Aiming at the problems that difficulties of locating target information， large time and space costs of traditional feature marking methods in the face of massive network data， a mutual information feature feedback marking method based on Weighted Genetic Algorithm is proposed. In this method， the data processing flow is optimized first， and the target data features are weighted to obtain an approximate global optimal solution. Then， the users mark text features or image instances， and a double supervision chart is constructed based on the user's marked and unmarked conditions. Finally， a real value speculation function is established and calculated to obtain unmarked nodes in the double supervision chart. The simulation results verify that the method has small error and high retrieval accuracy， and can quickly find the target content in a large amount of data.

Keywords： Weighted Genetic Algorithm; mutual information; double supervised graph; real valued function; approximate global optimal solution

0  引  言

随着社会步入大数据时代，各个行业都能收集到大量种类多且价值密度低的数据。各行各业都希望从PB级大数据中分析出潜在且有价值的数据，以获取更大的利益[1]。面对数量如此巨大的信息，想要从中找到自己需要的信息简直就如大海捞针一般困难，所以，如何在海量、无序化、多样繁杂的数据信息中快速找到所需的信息，是如今亟待需要解决的难题之一[2]。

在交互信息中寻找自己所需的信息，特征反馈标记方法就起到了很大的作用。也有不少相关学者对此展开研究。文献[3]提出一种新的模糊粗糙集模型，并将此模型应用于多标记特征选择。文献[4]认为可以利用模糊辨识关系，重新定义样本和标记的重要性度量，提出基于双空间模糊辨别关系的多标记特征选择算法。文献[5]提出基于互信息标记粒化的特征选择算法，先用聚类将标记粒化为多个标记粒，再基于最大相关和最小冗余准则进行特征选择。针对上述方法存在的问题，本文提出了基于加權遗传算法的互信息特征反馈标记方法。

1  标记特征选择分析

在多标记学习中，“维数灾难”问题一直困扰着研究者。“维数灾难”不仅提高了算法时空复杂度，同时也降低了学习器的精度。为此国内外学者提出了大量多标记降维方法。同单标记学习类似，可以将多标记降维方法分成两种类型，一种是多标记特征提取方法，另一种是多标记特征选择方法。常见的多标记特征提取的方法有偏最小二乘法（Partial Least Squares， PLS）、线性判别分析（Linear Discriminant Analysis， LDA）、典型关联分析法（Canonical Correlation Analysis， CCA）。虽然特征提取的方法对算法的分类性能有一定的提高，但提取出新的特征空间会失去原始特征空间的物理意义，换句话说就是破坏了原始特征空间的结构，这样分析出来的信息就会不尽如人意。因此，许多人就转而研究多标记特征选择方法[6-8]。

信息检索流程如图1所示。网民首先输入要检索的关键词或者是图片信息，系统根据任意排序函数给出Top-n个结果。如果用户对检索结果不满意，继续输入检索，系统根据用户再次输入的信息提供给用户待标记的文本特征或者图像实例[9，10]，用户完成标记后，标记了“相关”的文本特征或者图像实例的正例点的yi值赋予1，负例点为0。然后系统利用启发式视觉特征标注法（也称为混合反馈）和构建双重监督图的方法计算用户为标记的文本特征或者图像实例的f值，并对其进行排序后反馈给用户Top-n个检索结果，此过程直到用户检索到满意的结果终止。

2  基于加权遗传算法的网络数据特征反馈标记

2.1  加权遗传算法下加权计算

互信息是通过信息实时共享提供给用户最优的上网体验，通过对互信息数据进行融合与整理，确定统一的语义格式，以及信息的检索流程和传播规律，凭借加权遗传算法将用户赋予数据的多特征问题转换为单一特征进行计算。将m1、m2设为网络节点和特征信息的权重因子，使m1 + m2 = 1，根据权重因子，构建目标函数，并求解目标函数，获取全局最优解。

2.1.1  种群初始化

计算加权后m1、m2的成本值可获得近似全局最优解，那么即可通过编码的形式得到最优特征信息。在编码中按照实数编码的方式，假设有3个特征信息可供选择，编号分別为1、2、3；假设有10个基因位，将这3个特征信息随机与这10个基因位进行匹配。列举一个例子来更好地说明该方法：假设有10条染色体，分别为1，3，2，2，3，1，2，1，1，3，染色体的运动过程即为特征信息与基因位的匹配方式，那么就有特征信息1：0→1→6→8→9；特征信息2：0→3→4→7；特征信息3：0→2→5→10。0表示的是网络节点。这样就得到了一种算法，通过改变种群的大小就可得到不同数量的算法，完成种群的初始化。

2.1.2  交叉操作

假设Pc表示交叉概率，并且该值不变，再假定一个随机数值，将随机数的值与Pc值进行对比，如果Pc值大于随机数的值，则对染色体进行交叉操作，如果Pc值小于随机数的值，则不需要对染色体进行交叉操作。首先对染色体的交叉点进行确定，确定后对两条染色体进行交叉操作，从而获取全新的两条染色体，上述即为交叉操作的流程。

2.1.3  变异操作

假设Pm为变异概率，并且该值同样保持不变，再假定一个随机数值，将随机数的值与Pm值进行对比，如果Pm值小于随机数的值，则对染色体进行变异操作，首先对染色体的变异点进行确定，确定后对两条染色体进行变异操作，从而获取全新的两条染色体，上述即为变异操作的流程。

2.1.4  适应度计算及其排序

根据特征信息的成本值建立适应度函数，将所有染色体代入适应度函数中，根据所得结果按照从小到大的顺序进行排列。每一次迭代计算中，只保留最优染色体，所得结果即为近似全局最优解。

2.1.5  加权遗传步骤

加权遗传算法的基本步骤如图2所示。

1）创建初始种群NIND，染色体的个数设为NP个。

2）对染色体进行交叉操作。

3）交叉操作后，对染色体结构进行变异。

4）建立适应度函数，计算所有染色体的适应度函数并保留最优染色体。

5）设定迭代次数并进行迭代计算，找出最优染色体并对其进行加权计算。

6）找出近似全局最优染色体。

7）结束计算。

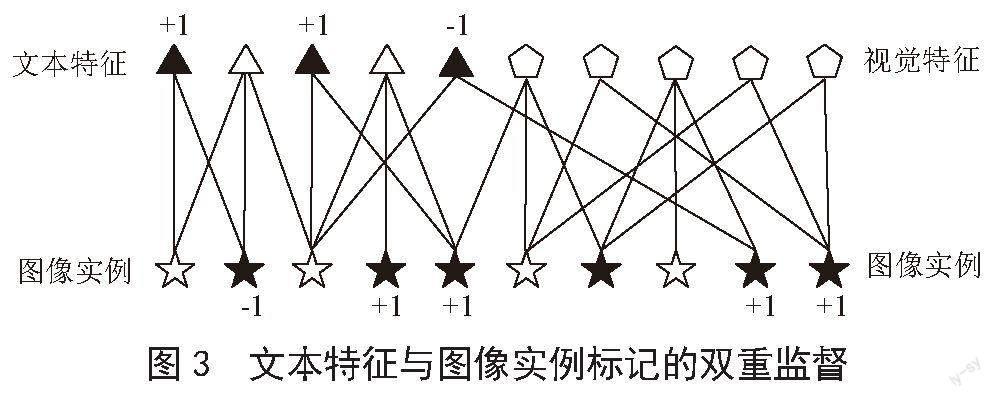
2.2  构建特征反馈标记的双重监督图

对互信息中的数据完成用户视角下数据特征的加权计算后，通过文本特征和图像实例进行特征反馈标记，这里采用构建双重监督图的方式来实现。假设网络中有n个图像实例、m个文本特征和k个视觉特征，使得t = n + m + k为特征信息总和。用户完成标记后，获得了l个数据信息（x1，y1），（x2，y2）…（xl1，yl1），（xl1+1，yl1+1）…（x1，y1），y1∈{-1，1}，其中，前l1个表示的是文本特征与标签，后l～l1个表示的是图像实例与标签。假设有u个特征未标记，那么u = n + m + k - l，其中l<

2.2.1  构建标记推测函数

在图像G上构建一个实数值函数f：V→?，使得图中所有的标记样本都满足条件：f （i ） ≡ fl （i ） ≡ yi。这里在基于图的半监督学习法的基础上，提出假设“相近的点具有相同的标记”，同理可知，相近的未标记的点也具有相同的标记。以此假设为基础，定义二次能量函数为：

式中，f表示标记样本i、j的实数值函数。

再利用高斯场为f函数定义一个概率分布：

其中，β表示逆温参数。Zβ在所有已经标记的样本中利用f函数进行了归一化处理。

2.2.2  计算推测函数

为了简便计算过程，将W矩阵分成4块：

综上所述，本文提出的基于加权遗传算法的互信息特征反馈标记方法的具体流程如图4所示。

3  仿真实验分析

为了验证本文提出的基于加权遗传算法的互信息特征反馈标记方法在实际应用中的有效性，进行一次仿真实验分析。将文献[3]方法和文献[4]方法作为对比方法，且文献[3]方法、文献[4]方法和本文方法所处的实验环境、网络条件以及用户对数据的反馈均为相同的。本文通过检索精度和效率来从侧面验证标记方法的优劣。对比结果如图5和表1所示。

从图5中的曲线变化可以看出，本文方法与其他两种方法相比有着较高的检索精度，且整体变化平稳，无较大的波动。

从表1中可以看出，与其他两种方法相比，本文方法有着较高的检索效率。这是由于本文利用加权遗传算法将复杂的用户反馈简化为单一问题计算，降低了冗余信息对反馈标记的干扰，同时减少了繁杂的计算过程，使标记结果更符合互信息用户需求。

4  结  论

为了让网民在海量的计算机数据中快速找到自己所需的信息，本文提出了基于加权遗传算法的互信息特征反馈标记方法。通过数据资源的融合与整理、数据资源特征反馈传播路径和信息检索步骤分析，采用加权遗传算法对特征信息进行加权计算，得到近似全局最优解，根据用户对特征信息的标记与未标记情况构建双重监督图以及实数值推测函数，更深层次的了解用户的需求。通过仿真对比实验，检验了所提的互信息特征反馈标记效果好、检索时间短、效率高及精度高，体现了所提方法的优越性。

参考文献：

[1] 孙林，徐枫，王振，等.基于标记权重和mRMR的多标记特征选择 [J].山西大学学报：自然科学版，2023，46（1）：40-52.

[2] 孙林，杜雯娟，李硕，等.基于标记相关性和ReliefF的多标记特征选择 [J].西北大学学报：自然科学版，2022，52（5）：834-846.

[3] 徐久成，申凯丽.基于双空间模糊邻域相似关系的多标记特征选择 [J].模式识别与人工智能，2022，35（9）：805-815.

[4] 程玉胜，李雨，王一宾，等.结合滑动窗口与模糊互信息的多标记流特征选择 [J].小型微型计算机系统，2019，40（2）：320-327.

[5] 卢舜，林耀进，吴镒潾，等.基于多粒度一致性邻域的多标记特征选择 [J].南京大学学报：自然科学版，2022，58（1）：60-70.

[6] 姚二亮，李德玉.多标记特征选择算法的综述 [J].郑州大学学报：理学版，2020，52（4）：16-27.

[7] 李闪闪，潘正高.基于互信息的多标记特征选择 [J].宿州学院学报，2019，34（5）：61-67.

[8] 廖大强.基于径向基函数神经网络的数据关联挖掘算法设计 [J].科技通报，2019，35（8）：125-128.

[9] 程玉胜，陈飞，王一宾.基于粗糙集的数据流多标记分布特征选择 [J].计算机应用，2018，38（11）：3105-3111+3118.

[10] 孙林，潘俊方，张霄雨，等.一种基于邻域粗糙集的多标记专属特征选择方法 [J].计算机科学，2018，45（1）：173-178.