一种新的变步长LMS 算法及其在语音降噪中的应用
张越,沈建明,王庆祥,陶冶博,王雷,罗必露
(嘉兴职业技术学院,浙江嘉兴,314036)
0 引言
传统的滤波器的频率响应是固定的,因而在滤波过程中只能对噪声与有用信号满足特定要求,即有用信号位于通带而噪声信号位于阻带,且两者在频谱上没有重叠时,才能取得最好的滤波效果。而在一些特定场景中,噪声信号与有用信号在频域上存在重叠部分,此时使用传统滤波器就无法获得良好的降噪效果。与传统滤波器相比,自适应滤波器的特殊之处在于其可以根据输入信号的滤波结果与期望信号的差值,在不改变滤波器结构的前提下,通过算法不断地迭代,实时更新滤波器的抽头系数,直至期望信号与滤波结果的差值收敛到一定的范围以内时,滤波器的抽头系数也趋于稳定。正是由于自适应滤波算法对噪声的跟踪特性,使得其为语音降噪领域的研究提供了新思路,即不再被动的通过物理隔离等手段降低语音信号中的噪声,而是主动的制造与语音信号中噪声等幅反相的噪声并进行抵消,从而达到主动降噪的效果。
最小均方(Least Mean Square)LMS 算法是一种典型的自适应滤波算法,由于其具有结构简单,计算量小的优点,所以被广泛地应用于噪声消除等领域[1~2]。为了解决传统LMS 算法收敛速度与稳态误差难以同时达到理想状态这一问题,本文提出了一种新的变步长LMS 算法,比较了其与经典LMS 算法在收敛速度与稳态误差方面的表现,并将其应用到了语音降噪领域以验证算法的性能。
1 LMS 算法简介
■1.1 经典LMS 算法及在语音降噪中的应用
经典的LMS 算法在1959 年由Windrow 和Hoff 两位学者提出的,其典型结构如图1 所示。

图1 LMS 滤波器结构示意图
其中x(n)分为两路,一路作为进入滤波器的参考噪声,另一路经过未知系统后,和与x(n)不相关的信号v(n)混合,成为待处理目标信号d(n)。y(n)为信号x(n)经过自适应滤波器滤波后的结果,e(n)为目标信号d(n)与y(n)之差。
从结构上看,整个LMS 滤波器可以看作一个阶数固定,系数可变的横向滤波器,其系数由LMS 算法迭代产生,具体算法如下:
其中,n 为迭代次数,w(n)为第n 次迭代后得到的横向滤波器系数,µ为迭代步长,µ的取值范围为[0,1/λ],其中λ 是x(n)自相关矩阵的最大特征值。
经过多次迭代后,自适应滤波器的输出y(n)与x(n)经过未知系统后的输出x1(n)之间的差值会逐渐减小,滤波器系数也会趋于收敛。
主动语音降噪的主要原理就是对参考噪声进行自适应滤波后与有用信号中混杂的噪声进行对消。其算法示意图如图2 所示,在进行语音降噪实现时,在噪声源与语音源附近各设置一音频接收装置,此时信号v(n)被所需语音信号s(n)取代,而未知系统即为由参考噪声接收装置至待降噪语音接收装置的空间与电子设备所构成的噪声信道。噪声源处采集到的信号x(n)作为参考噪声输入系统,而在语音信号附近收集到的目标信号d(n)中,既包含有用信号s(n),也包含了经过由噪声源至语音信号处的空间信道滤波后的x1(n)。根据自适应算法原理可知,当算法收敛时,滤波器输出y(n)会与x1(n)近似相等,则d(n)与e(n)抵消后的结果e(n)即为降噪后语音信号s(n)。
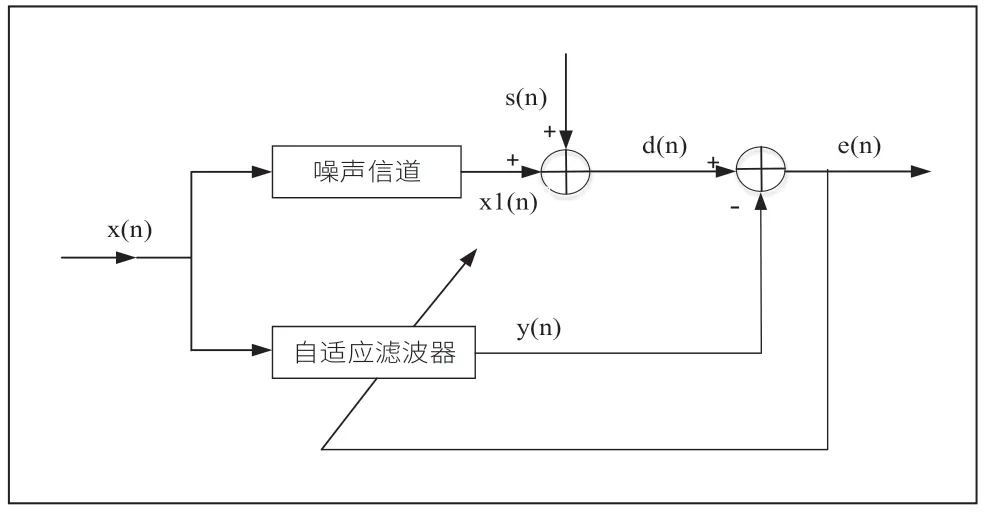
图2 LMS 语音降噪示意图
■1.2 变步长LMS 算法
经典的LMS 算法虽然具有结构简单,计算量小,易于实现等优点,但由其算法可知,其迭代步长µ为一固定值,当µ值取值较小时,算法收敛速度降低,但收敛后稳态误差较小;而当µ值取值较大时,可以提升算法的收敛速度,但会导致稳态误差增大,甚至引起震荡现象。这一特性会导致该算法在实际应用中面临收敛速度与稳态误差不可兼得的问题。
为了解决以上问题,已经有大量的研究者进行了研究并提出新的算法[3~9]。一种主流的方法是通过构建迭代步长µ与误差e之间的非线性关系,使得在算法的起始阶段,迭代步长µ的取值较大,从而获得较快的收敛速度;而在算法接近收敛时,迭代步长µ取值趋近于零,从而降低稳态误差。在已有研究中,文献[3]基于S 函数构造了变步长模型,文献[4]基于指数函数构造了变步长模型,文献[5]、文献[6]基于对数函数构造了变步长模型,除此之外,还有学者提出了基于箕舌线,反正切和双曲正切构造的变步长模型[7~9]。这些算法都在某些方面取得了良好的效果,但也存在着一些不足,如文献[3]中S 函数模型在曲线底部较为陡峭,导致稳态误差增大;文献[5]中的算法模型在误差e尚未达到零时步长µ已变为零,影响算法性能;文献[9]中的算法模型过于复杂,导致计算量过大,缺少灵活性等。
2 改进的变步长LMS 算法
■2.1 变步长LMS 算法模型
由前文可知,在良好的变步长LMS 算法中,其步长误差曲线应该在误差较大和接近零时具有更为分化的特性,即当误差较大时,步长误差曲线应该较为陡峭,使得随着误差的增大,步长取值可以迅速增大以提高收敛速度;当误差较小时,步长误差曲线应该趋于平缓,使得算法在接近收敛时,步长取值不会剧烈变化,避免导致稳态误差的提升乃至引起震荡。对数函数由于其自身的特性,在进行适当的变换后,可以较好的满足这一要求。因此,本文以对数函数为原型,提出了一种改进的变步长LMS 算法,算法中步长µ和误差e的对应关系如式1 所示:
其中a,b 为参数,参数a 用于控制算法的幅值,参数b 用于控制曲线的形状。通过对该式进行分析可知,当误差e趋近于零时,步长µ也趋近于零,由此避免了µ提前归零导致的稳态误差增大的情况。同时,由于对数函数曲线具有良好的下降特性且其运算相对简单,因而在保证了算法性能的同时降低了计算复杂度。
■2.2 参数对步长误差曲线的影响
参数a,b 对步长µ与误差e的关系曲线的影响情况如图3、图4 所示。

图3 参数a 取不同值时本文算法步长误差关系曲线

图4 参数b 取不同值时本文算法步长误差关系曲线
图3 为参数b 取值为1,参数a 取值分别为0.8,1,1.2时的步长误差关系曲线,对图3 进行分析可知,参数a 对步长幅值的线性调整主要体现在误差较大的阶段,即函数尚未收敛时,增大a 值可提高算法的迭代步长,减小a 值可降低算法的迭代步长。
图4 为参数a 取值为1,参数b 取值分别为0.5,1,1.5时的步长误差关系曲线,对图4 进行分析可知,参数b 主要影响误差步长曲线的开口大小,参数b 取值越大,曲线在接近收敛时梯度越大,步长在误差趋近于零时的下降幅度越大,算法曲线在尚未收敛和接近收敛时的特性差异越明显。
■2.3 最佳参数的选取
本文通过仿真结果来进行最佳参数的选择,仿真条件为:
(1)自适应滤波器的阶数为2;
(2)系统的初始滤波器系数为[0.8,0.5];
(3)x(n)选用均值为0,方差为1 的高斯白噪声;
(4)v(n)选用均值为0,方差为0.04,且与x(n)不相关的高斯白噪声;
(5)仿真点数为512,为了排除单次仿真极端值的干扰,获得更为准确的收敛曲线,每组参数取值下均进行200次重复实验,对每次实验的迭代误差的绝对值取算术平均值后,再绘制该组参数下的收敛曲线。
图5 为参数b 取值为1,参数a 取值分别为0.2,0.5,0.8时本文变步长LMS 算法的收敛曲线,由图可知当参数a 从0.2 上升到0.5 时,算法的收敛速度显著提升;但当参数a继续上升至0.8 时,算法的收敛速度无明显上升,且在收敛起始阶段产生了不稳定的震荡。考虑到其他因素的综合影响,参数a 的最佳取值应该选择在0.2 到0.5 之间。
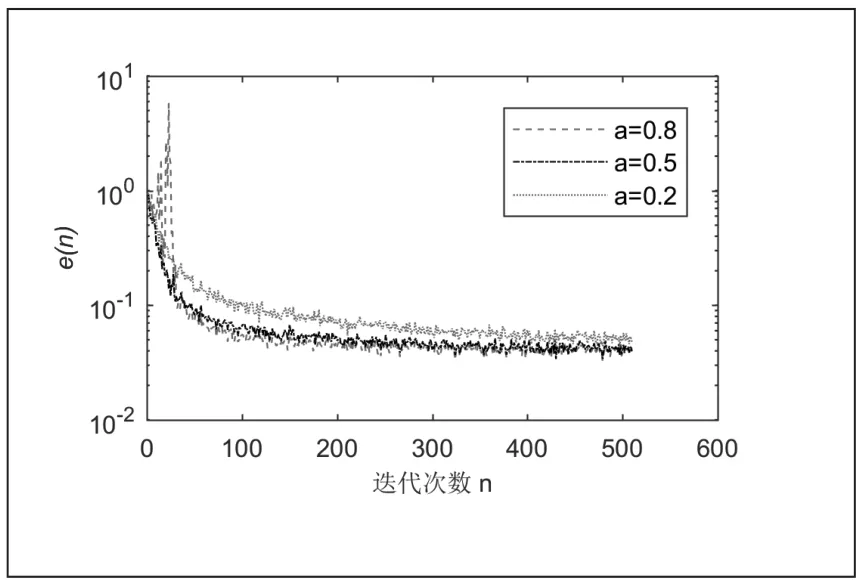
图5 参数a 取不同值时本文算法收敛曲线
图6 为参数a 取值为0.3,参数b 取值分别为1,30,50时本文变步长LMS 算法的收敛曲线,由图可知当参数b 从1 上升到30 时,算法的收敛速度显著提升;但当参数b 由30 继续上升至50 时,算法的收敛速度已无明显上升,且在收敛后稳态误差有所增加。综合考虑,参数b 的最佳取值应选择为30 左右。

图6 参数b 取不同值时本文算法收敛曲线
■2.4 算法性能对比
为了比较本文提出的变步长LMS 算法与已有算法的性能,本文将该算法与文献[6]中算法在2.3 节所介绍的仿真条件下进行测试,并进行对比。在参数的选取上,本文算法中选择当前仿真环境下的算法性能最优时的参数;参数a为0.3,参数b 为30;文献[6]中算法同样选择当前仿真环境下算法性能最优时的参数:参数1 为0.15,参数2 为0.6。
算法性能对比结果如图7 所示,从对比结果可以看出,不论是算法的收敛速度,还是算法收敛以后的稳态误差,本文算法均优于文献[6]提出的算法。
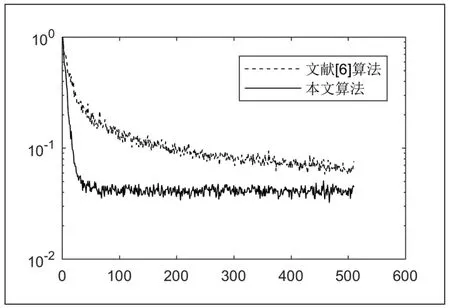
图7 本文算法与文献[6]算法性能对比
3 变步长算法在语音降噪中的应用
为了验证本文提出的变步长LMS 算法在语音降噪领域的应用,本文按照图2 结构设置了实验进行测试。其中,参考噪声x(n)采用均值为0,方差为0.01 的高斯白噪声,待降噪信号为录制人声音频与x(n)经模拟信道后相加所得混合信号,自适应滤波器阶数为8。同时,根据第三节所分析的最佳参数范围,根据实际降噪效果确定参数a 与参数b,通过在参考值附近进行多次测试确定最优值,测试结果证明,参数a 为0.2,参数b 为20 时降噪效果最佳。
图8 为参考噪声信号和包含噪声的音频信号;图9 为使用本文提出的变步长LMS 算法降噪后得到的音频信号和降噪后音频信号与原始音频信号之间的误差;图10 为使用传统的定步长LMS 算法降噪后得到的音频信号和降噪后音频信号与原始音频信号之间的误差。
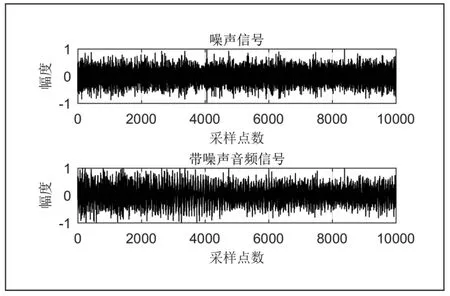
图8 参考噪声与带噪音频信号

图9 本文变步长LMS 算法降噪效果及与原信号误差

图10 传统LMS 算法降噪效果及与原信号误差
可以看到,本文提出的算法对宽带白噪声具有良好的滤除效果,同时相较于传统的固定步长的LMS 算法,本文提出的算法收敛更快,并具有更小的稳态误差。经测试,使用本文算法降噪前信噪比为8.5dB,降噪后性噪比为61.4dB,信噪比提升为52.9dB,降噪效果显著。
4 总结
本文提出了一种新的变步长LMS 算法,对算法进行了理论分析并讨论了其最优参数的取值。与相关文献提出算法进行的对比测试表明,本文算法不论是在收敛速度还是在稳态误差上均有更好的表现。最后,将本文所提出算法应用于语音降噪领域并取得了良好的效果。如何进一步优化模型使其易于在单片机或FPGA 等平台上实现,将是下一步的研究方向。

